Function Mastery - AP Precalclus (2024)

Formula/Equation - Linear Function

f(x) = mx + b

m: slope

b: y-intercept

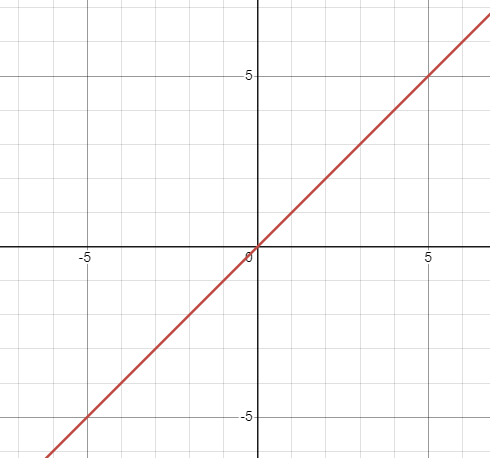
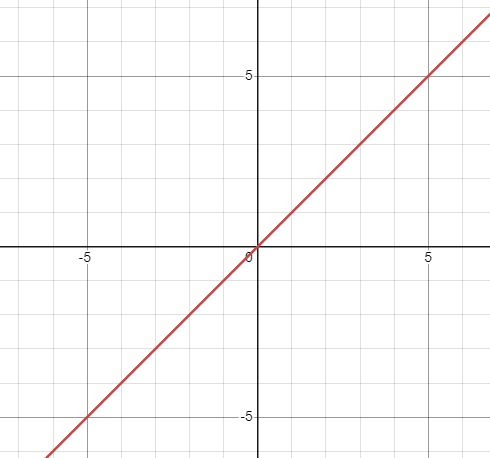
Domain & Range - Linear Function

Domain: (-∞, ∞)

Range: (-∞, ∞)

Formula/Equation - Quadratic Function

f(x) = a × (b(x + c))² + d

a: vertical stretch/compress

b: horizontal compress/stretch (b > 0, compress horizontally)

c: horizontal phase shift (-c = right c)

d: vertical phase shift

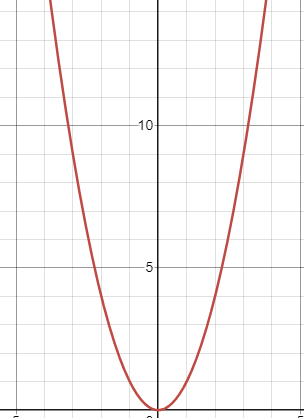
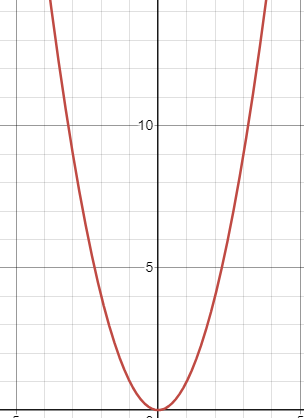
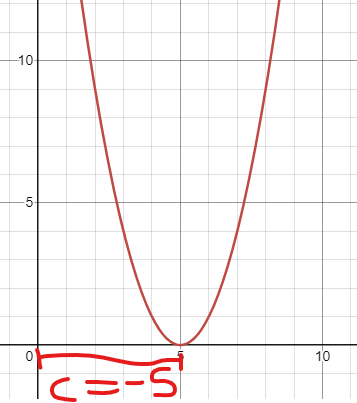
Domain & Range - Quadratic Function

Domain: (-∞, ∞)

Range: [d, ∞)

Horizontal Stretch/Compress - All Rectangular Functions

Stretch: 0 < a < 1

Compress: a > 1

---

Stretch: 0 < b < 1

Compress: b > 1

Vertical Stretch/Compress - All Rectangular Functions

Stretch: a > 1

Compress: 0 < a < 1

---

Stretch: b > 1

Compress: 0 < b < 1

Phase Shift - All Rectangular Functions

Shift Left: +c

Shift Right: -c

Formula/Equation - Cubic Function

f(x) = a × (b(x + c))³ + d

a: Vertical Stretch

b: Horizontal Stretch

c: Horizontal Phase Shift (-c = right c)

d: Vertical Phase Shift

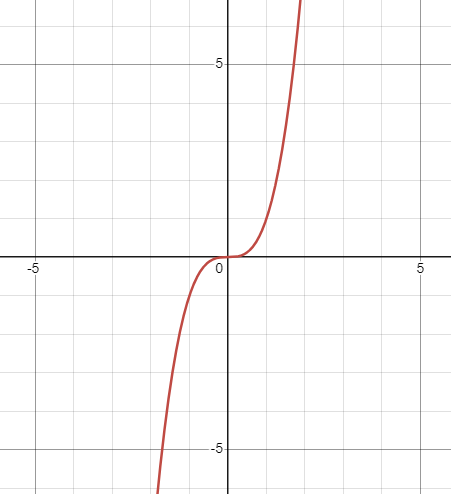
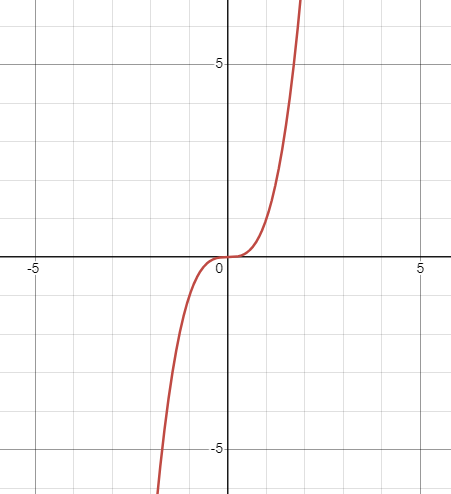
Domain & Range - Cubic Function

Domain: (-∞, ∞)

Range: (-∞, ∞)

Formula/Equation - Square Root Function

f(x) =a × √(b(x + c)) + d

a: Vertical Stretch

b: Horizontal Stretch

c: Horizontal Phase Shift

d: Vertical Phase Shift

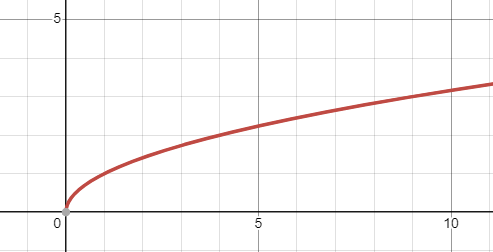
Domain & Range - Square Root Function

Domain: [-c, ∞)

Range: [d, ∞)

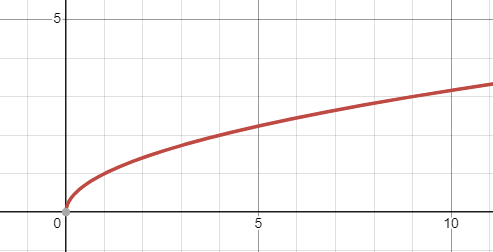
Inverse of what? - Square Root Function

Inverse of Quadratic function.

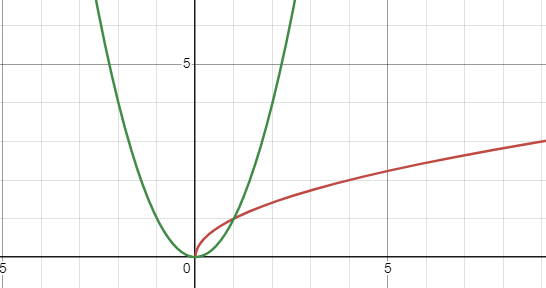
Formula/Equation - Rational Function

f(x) = (Zeroes) / (Vertical Asymptotes)

Horizontal Asymptotes - Rational Function

(n = degree)

Nⁿ < Dⁿ —> y = 1

Nⁿ = Dⁿ —> (N Ceofficent) / (D Ceofficient)

Nⁿ > Dⁿ —> (No Horizontal Asymptote)

Slant Asymptotes - Rational Function

Exists if Nⁿ -1 = Dⁿ e(If N degree is exactly one greater than of D)

To find slant asymptote:

1. Use long division or synthetic division.

2. Divide the numerator with the denominator

3. Ignore remainder

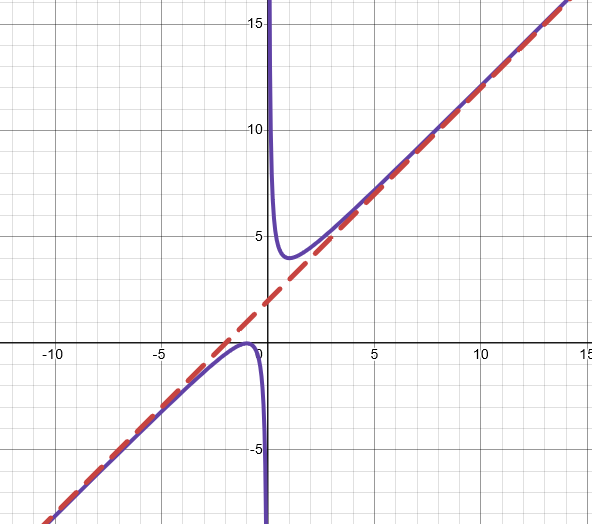
Formula/Equation - Exponential Function

f(x) = a × b^{(x + c)}

a: Vertical Stretch

b: Horizontal Stretch

c: Horizontal Phase Shift

d: Vertical Phase Shift

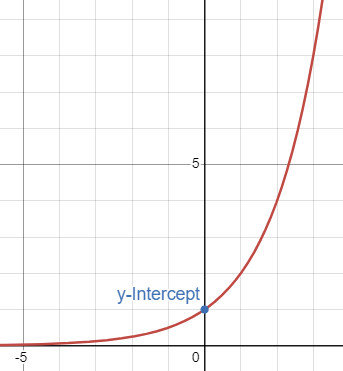
Domain & Range - Exponential Function

Domain: (-∞, ∞)

Range: (0, ∞)

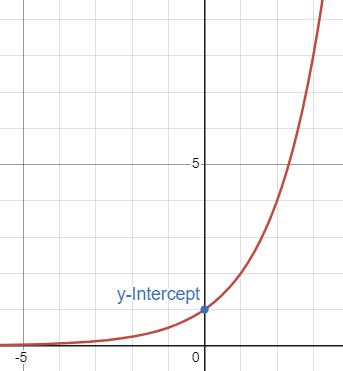
Horizontal Asymptote - Exponential Function

HA at value a.

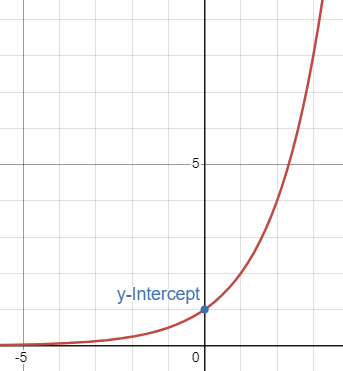
Growth - Exponential Function

When b > 1

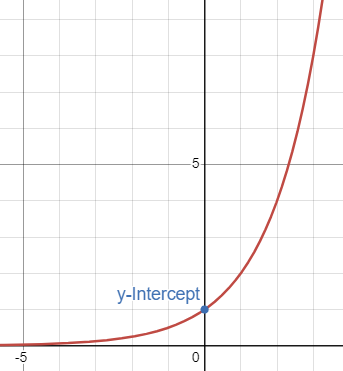
Decay - Exponential Function

When 0 < b < 1

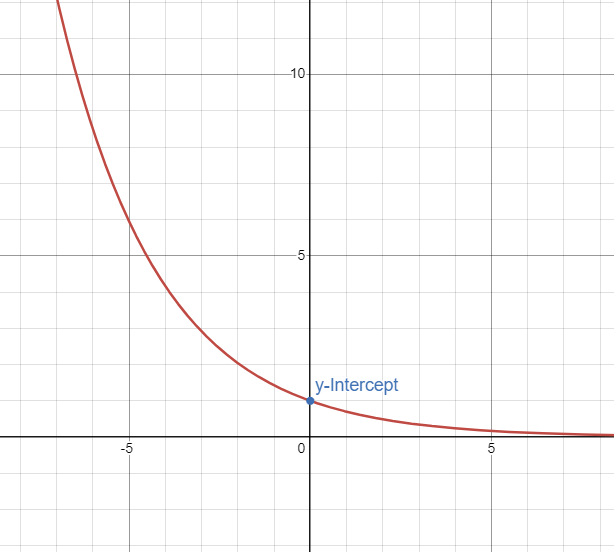
Formula/Equation - Logarithmic Function

f(x) =a × log_b(x + c) + d

a: Vertical Stretch

b: Horizontal Stretch (Note: reciprocated)

c: Horizontal Phase Shift

d: Vertical Phase Shift

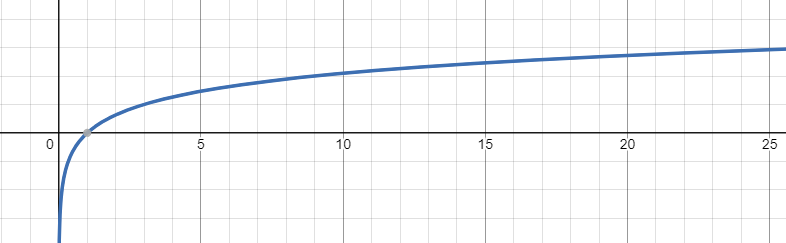
b Limitation - Logarithmic Function

MUST: B > 0

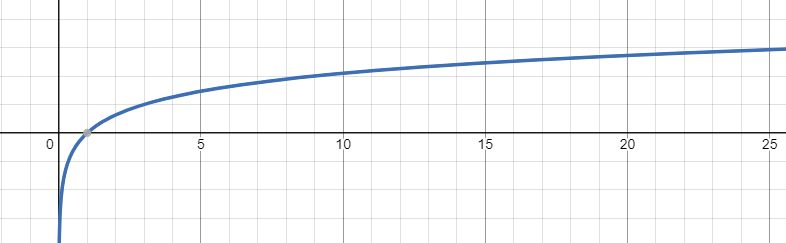
Vertical Asymptote - Logarithmic Function

VA at -c. (Horizontal Phase Shift)

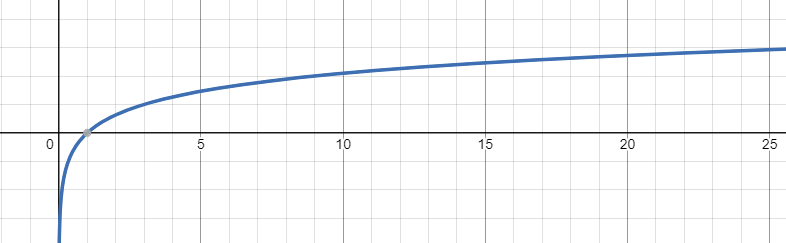
Domain & Range - Logarithmic Function

Domain: (0, ∞)

Range: (-∞, ∞)

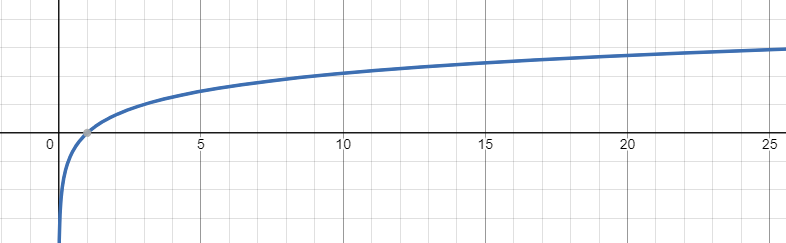
Inverse Function of what? - Logarithmic Function

Inverse of Exponential Function

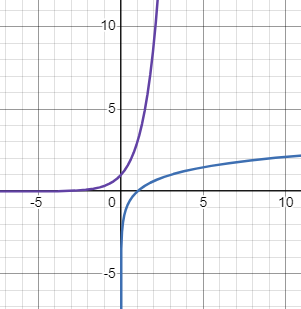
Growth - Logarithmic Function

When b > 1

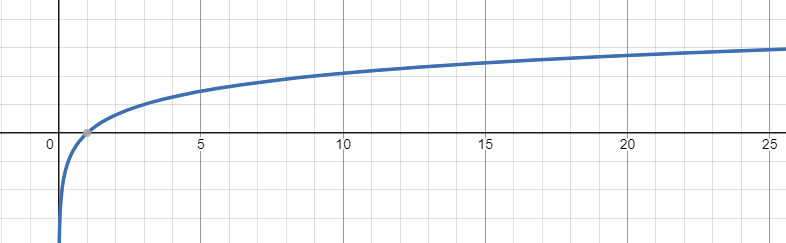
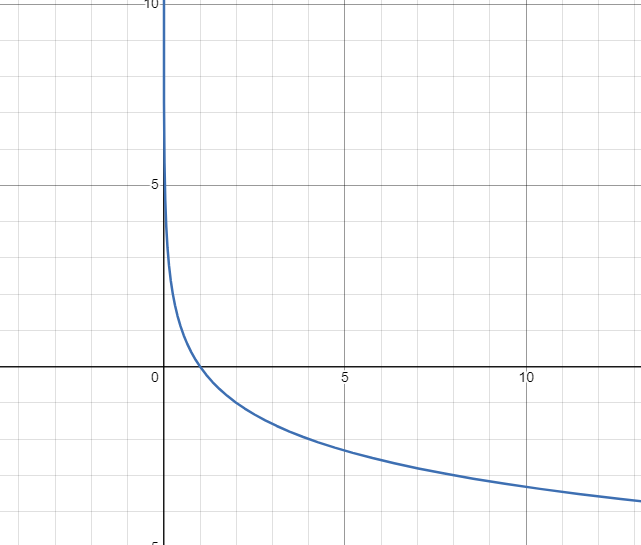
Decay - Logarithmic Function

When 0 < b < 1

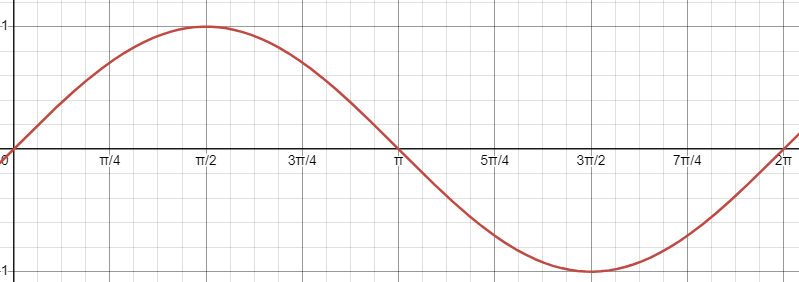
What is a period? (Def & Equation)

A single cycle of a periodic function.

Period = 2π / b

Exception for tangent: Period = π / b

Formula/Equation - Sine Function

f(x) = a × sin(b(x + c)) + d

a: Vertical Stretch

b: Horizontal Stretch

c: Horizontal Phase Shift

d: Vertical Phase Shift

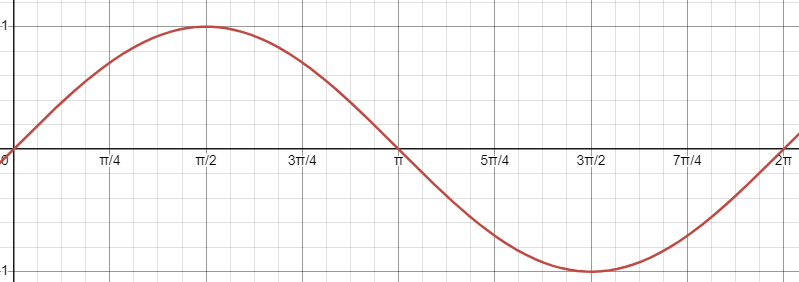
Domain, Range, & Period - Sine Function

Mid - Max - Mid - Min - Mid

Domain: [0, 2π]

Range |a|: [-1, 1]

Period: 2π / b

Midline: y = d

Starts at Mid

Formula/Equation - Cosine Function

f(x) =a × cos(b(x + c)) + d

a: Vertical Stretch

b: Horizontal Stretch

c: Horizontal Phase Shift

d: Vertical Phase Shift

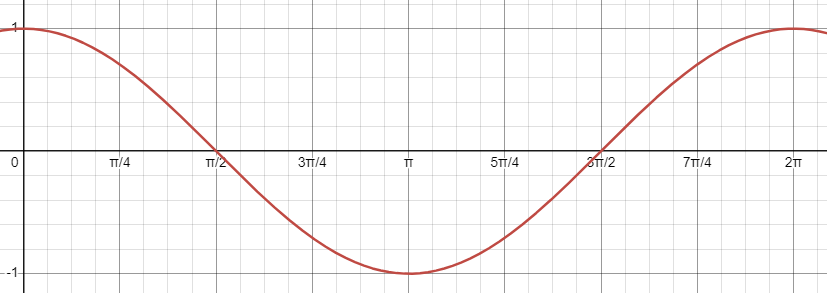
Translating Sine Function ←→ Cosine Function

sin(x) = cos(x - π/2) [Shifts right]

cos(x) = sin(x + π/2) [Shifts left]

Domain, Range, & Period - Cosine Function

Max - Mid - Min - Mid - Max

Domain: [0, 2π]

Range |a|: [-1, 1]

Period: 2π / b

Midline: y = d

Starts at Max

Formula/Equation - Tangent Function

f(x) = a × tan(b(x + c)) + d

a: Vertical Stretch

b: Horizontal Stretch

c: Horizontal Phase Shift

d: Vertical Phase Shift

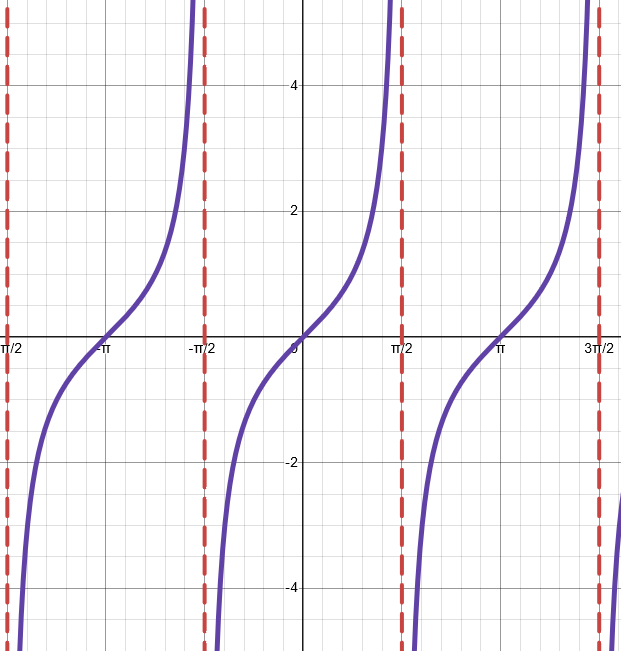
Domain, Range, & Period - Tangent Function

Domain: (-π/2, π/2)

Range |a|: (-∞, ∞)

Period: π / b (Parent Period: π)

Midline: y = d

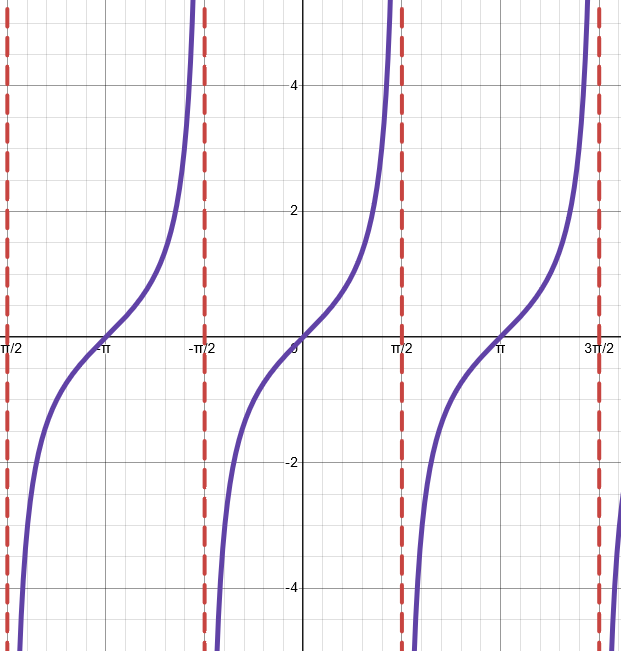
Asymptotes - Tangent Function

Each asymptote occurs at: π/2 ± πn where n ∈ ℤ

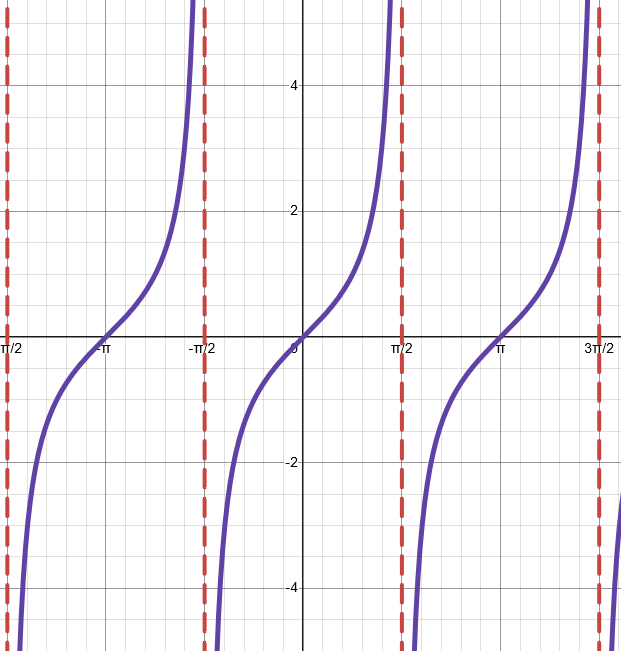
Define the notation: a ∈ ℤ

variable a is a set of all integers.

Formula/Equation - Cosecant Function (csc)

f(x) = a × csc(b(x + c)) + d

a: Vertical Stretch

b: Horizontal Stretch

c: Horizontal Phase Shift

d: Vertical Phase Shift

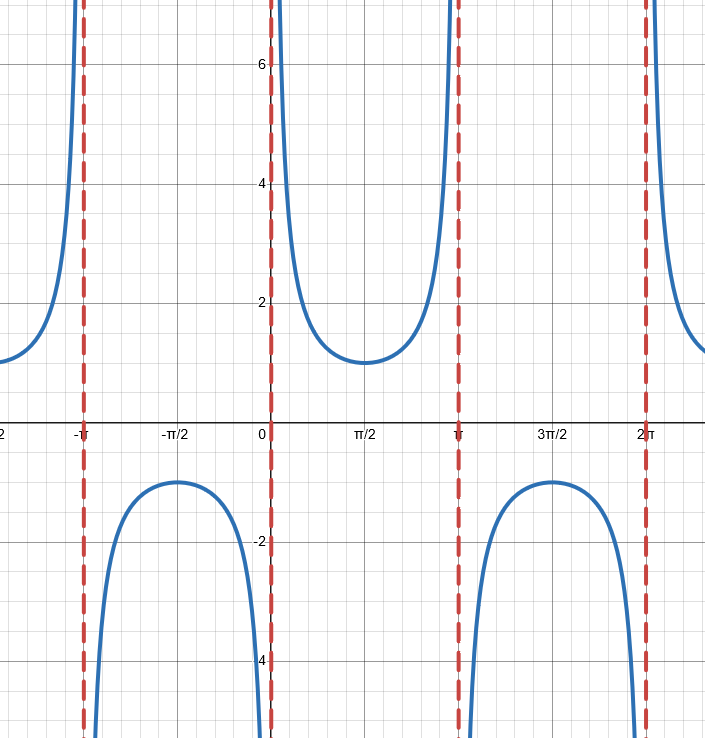
Domain, Range, & Period - Cosecant Function (csc)

Domain: (0, π) (of course changes with shifts)

Range: [a, ∞) & (-∞, -a]

Period: π / b (Parent Period: π)

Midline: y = d

Reciprocal of what? - Cosecant Function (csc)

Reciprocal of sin.

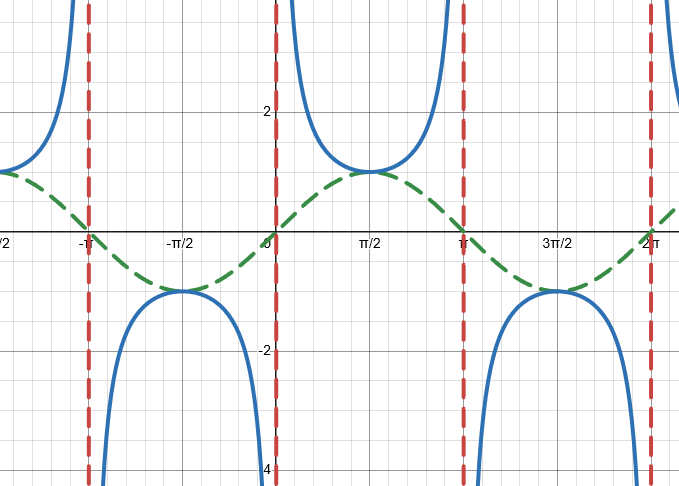
Formula/Equation - Secant Function (sec)

f(x) = a × sec(b(x + c)) + d

a: Vertical Stretch

b: Horizontal Stretch

c: Horizontal Phase Shift

d: Vertical Phase Shift

Domain, Range, & Period - Secant Function (sec)

Domain: (-π/2, π/2)

Range: [a, ∞) & (-∞, -a]

Period: π / b (Parent Period: π)

Midline: y = d

Reciprocal of what? - Secant Function (sec)

Reciprocal of cos.

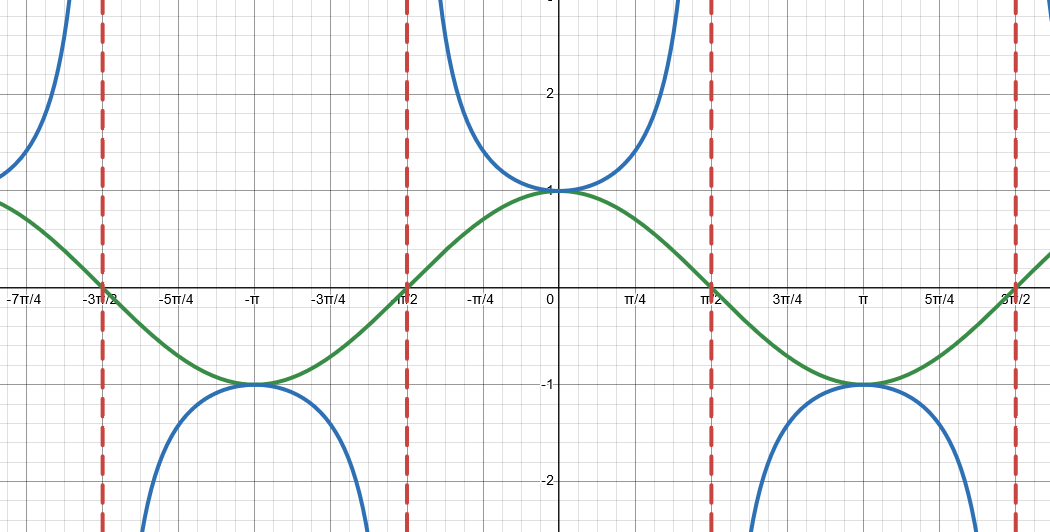
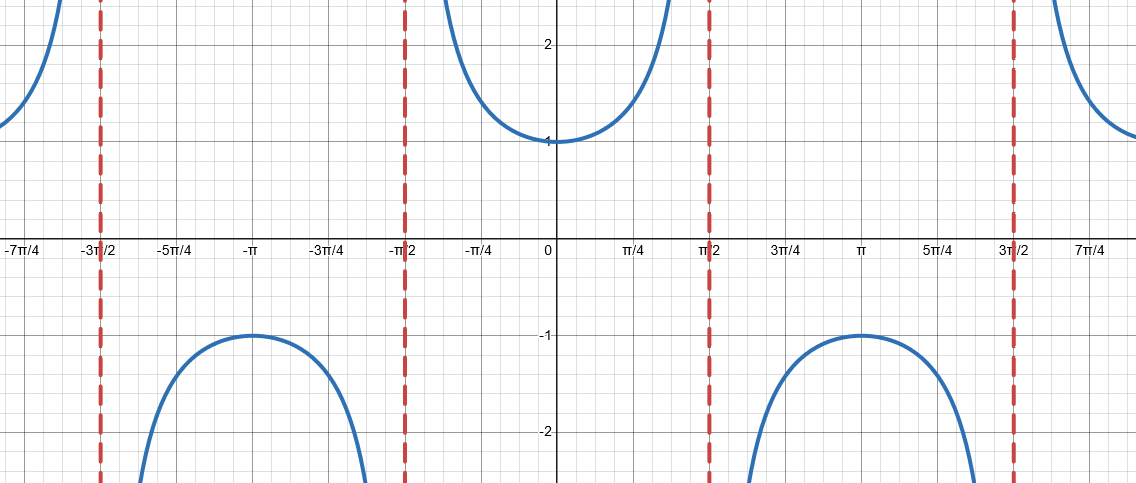
Formula/Equation - Cotangent Function (cot)

f(x) = a × cot(b(x + c)) + d

a: Vertical Stretch

b: Horizontal Stretch

c: Horizontal Phase Shift

d: Vertical Phase Shift

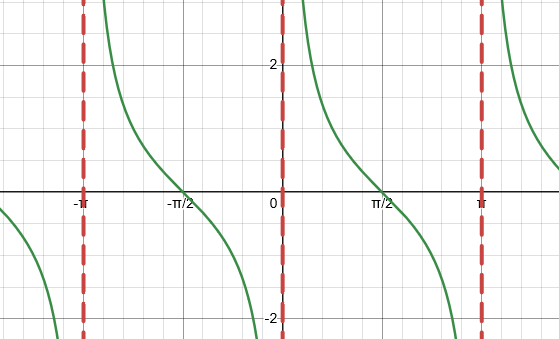
Domain, Range, & Period - Cotangent Function (cot)

Domain: (0, π)

Range: (-∞, ∞)

Period: π / b (Parent Period: π)

Midline: y = d

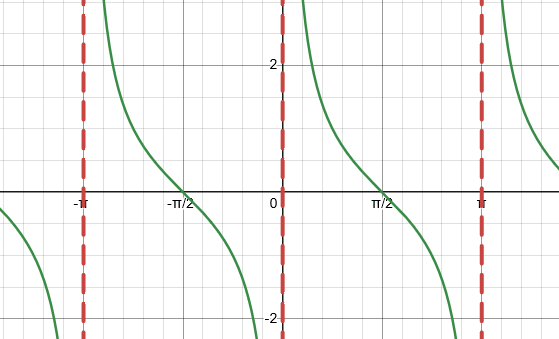
Reciprocal of what? - Cotangent Function (cot)

Reciprocal of tan.

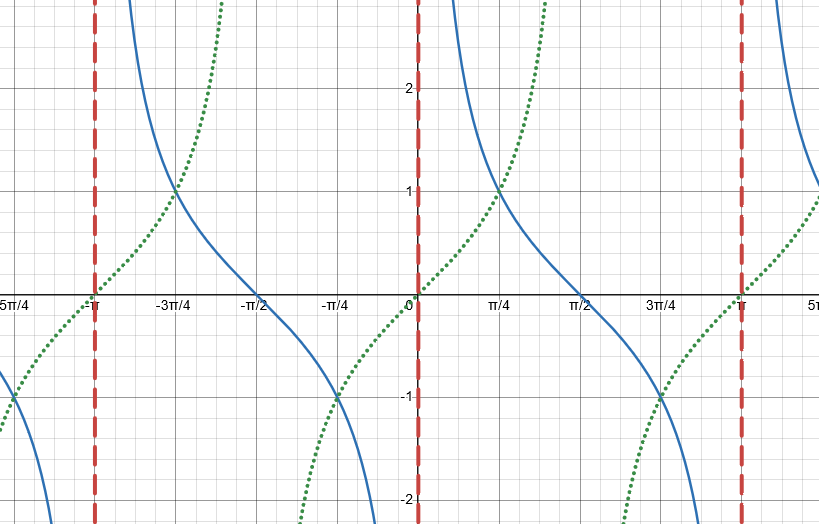
Domain & Range - Inverse Sine Function (Arcsin)

Domain: [-1, 1]

Range: [π/2, -π/2]

Domain & Range - Inverse Cosine Function (Arccos)

Domain: [-1, 1]

Range: [0, π]

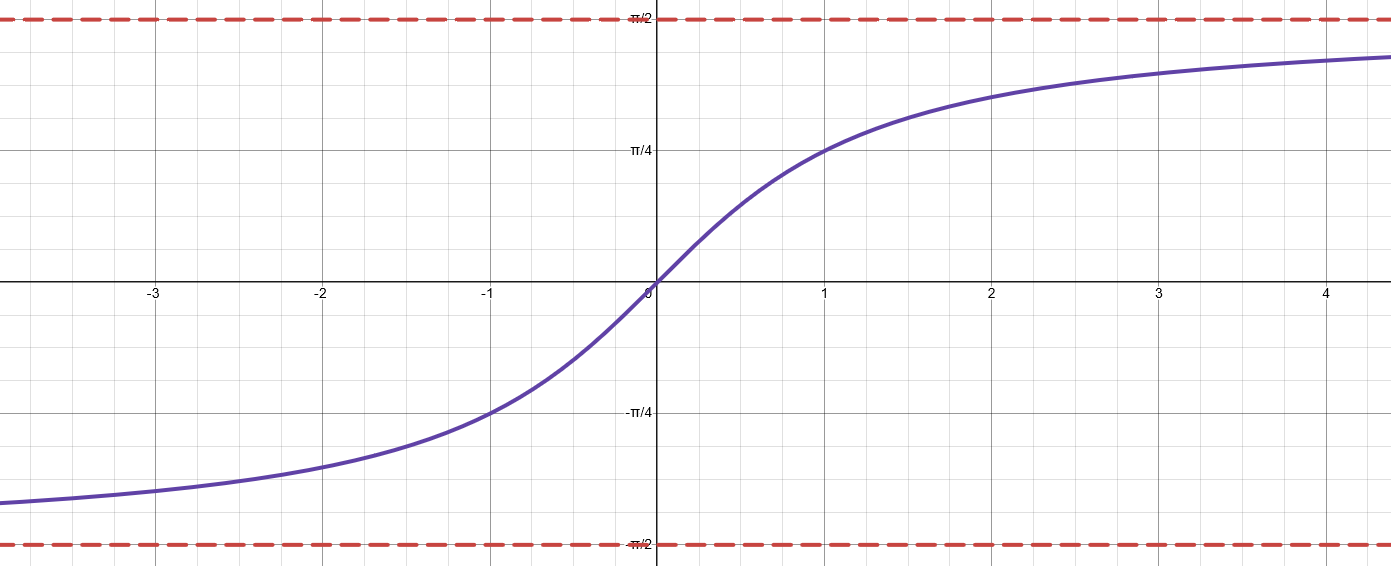
Domain & Range - Inverse Tangent Function (Arctan)

Domain: (-∞, ∞)

Range: (π/2, -π/2)

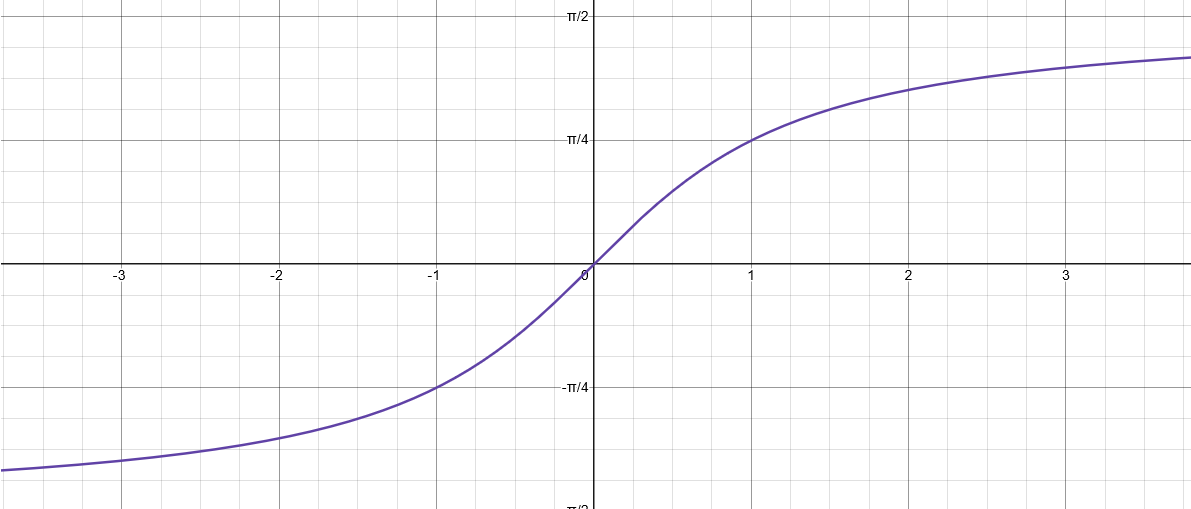
Asymptotes - Inverse Tangent Function (Arctan)

Two Vertical Asymptotes:

y = (π × a)/2

y = -(π × a)/2

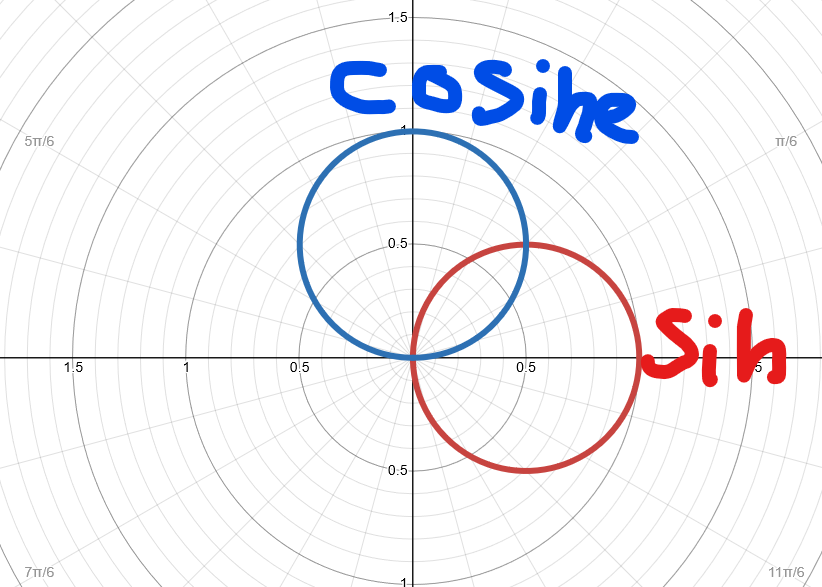
Cosine vs. Sin Polar Function

Cosine functions are ALWAYS on the x-axis

Sine functions are ALWAYS on the y-axis

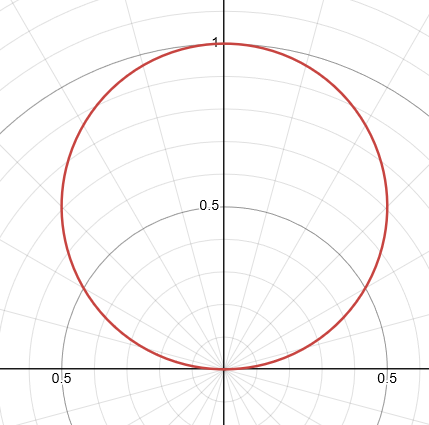
Formula/Equation - Polar Circle Function

r = a × sin(θ)

a: amplitude/scale

Domain - All Limacone Functions

Domain: [0, 2π]

(Except for even rose curves)

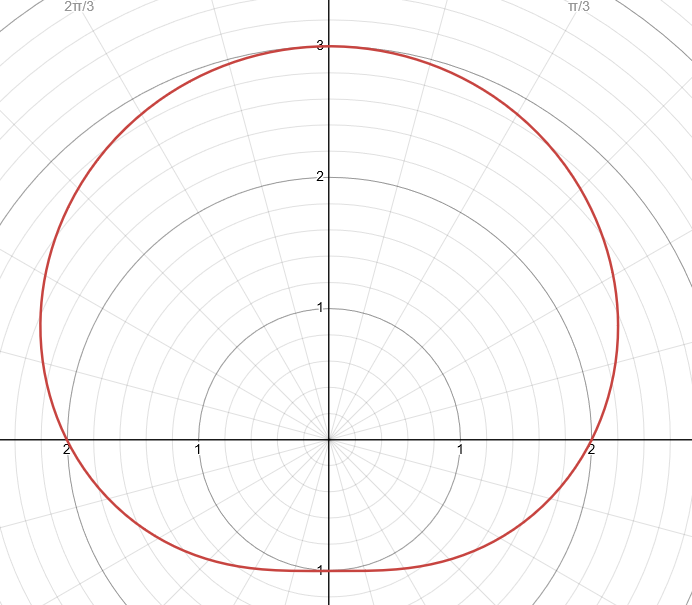
Formula/Equation - Polar Cardioid Limacone Function

r = a ± b × sin(θ)

MUST: (a / b) = 1

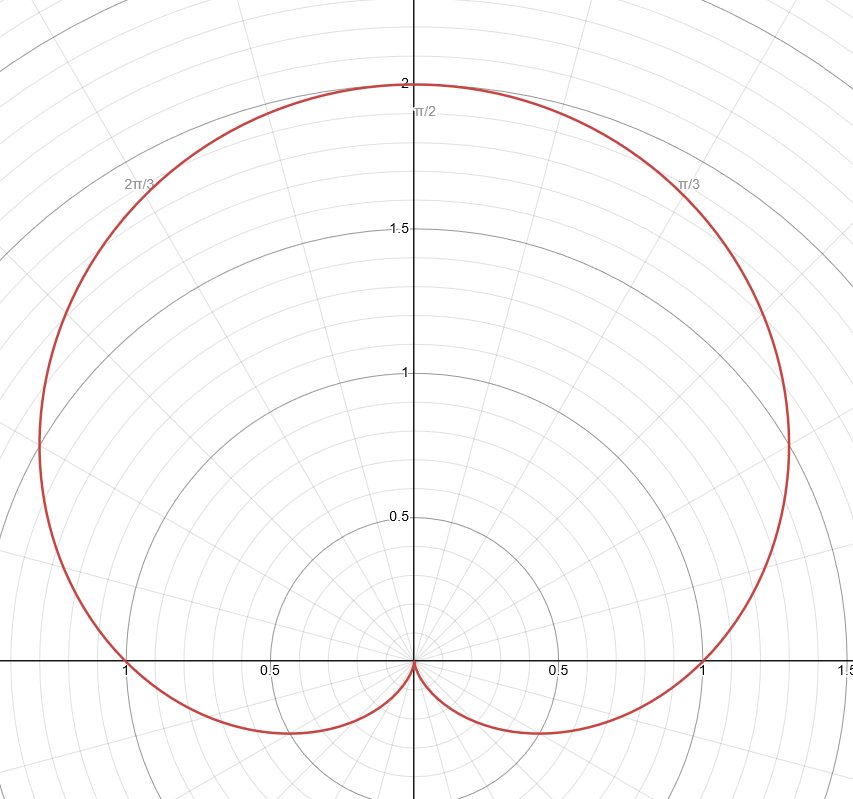
Formula/Equation - Polar Dimpled Limacone Function

r = a ± b × sin(θ)

MUST: 1 < (a / b) < 2

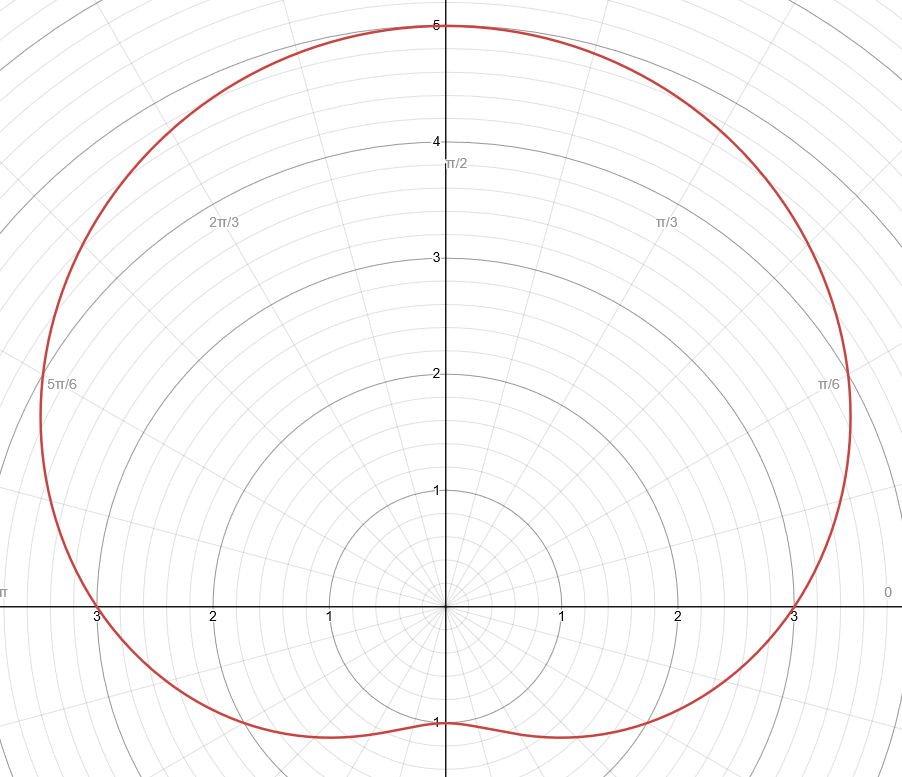
Formula/Equation - Polar Convex Limacone Function

r = a ± b × sin(θ)

MUST: (a / b) > 2

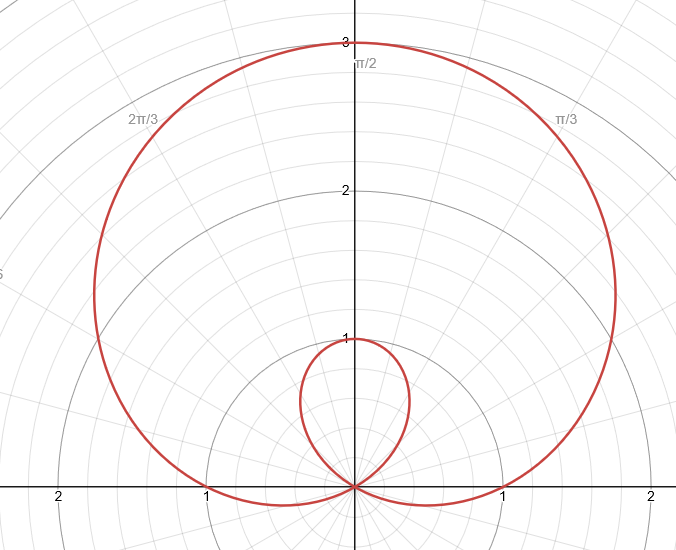
Formula/Equation - Polar Inner-loop Limacone Function

r = a ± b × sin(θ)

MUST: (a / b) < 1

Formula/Equation - Polar Rose Curves Function

r = a × sin(n × θ)

a: Amplitude

n: number of petals

Double petals when n is even

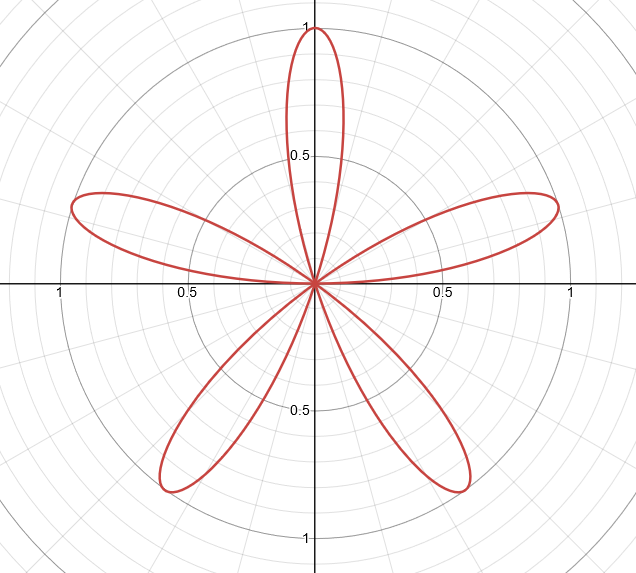
When n is odd - Polar Rose Curves Function

graph has n petals.

Domain: [0, π]

When n is even - Polar Rose Curves Function

graph has 2n petals. (Double)

Domain: [0, 2π]

Note: Even Sin Rose Curves Function’s petals do not intercept x or y axis.