Research & Statistics Exam I

Nominal

Applies a label

Numbers do not represent amounts of anything - they only distinguish groups

Numbers have no meaning

Ordinal

Ranking

Quantitative

Interval

Information about distance between points on the scale

No meaningful zero point

The Likert Scale

Ratio

Meaningful zero point

Examples:

how many jelly beans were eaten

multiple choice questions answered correctly

income

time

Independent Variable (IV)

The factor that the researcher changes or controls

Manipulates in an experiment to see it’s effect on another variable

Categorical

Exactly two levels

Dependent Variable

The outcome or effect being measured that changes in response to manipulations

Quantitative

On the interval scale

Descriptive Statistics

Simply describing your sample

Measures of central tendency (mean, median, mode)

Measures of validity (range, standard deviation)

Inferential Statistics

Inferring something about what’s happening in the population based on what we found in our sample

Conducting Inferential Statistics Research

On a sample (subset) taken from the entire population of interest

Sampling Distribution

A theortical distribution consisting of the mean scores for all possible random samples of a given size that can be drawn from a population

Central Limit Theorem

The mean of the sampling distribution = mean of the population

The sampling distribution becomes more normal as N increases

Degrees of Freedom

The number of scores in a dataset that are free to vary (i.e., take on any value) given a particular mean

The Degrees of Freedom Determine

The shape of the sampling distribution

Null Hypothesis

States that no differences exist

• Our IV has no effect

• There is no relationship

The Null Hypothesis is Always Stated in

Population terms - we are trying to characterize what’s going on in the population

p value

The probability of getting your outcome, if the outcome is true

Every Sample Mean has

A probability associated with it

Alpha

The area under the curve

Does not change at any point in the process

Alpha in a Directional One Tailed Test

It is put on one side of the distribution

When do we Reject the Nul Hypothesis

If p ≤ .05

If you Reject the Null Hypothesis you have Achieved

Statistical Significance

Critical Value

Will always have p = α

p = α : α

Area under the curve

It is always constant

p = α : p

The value of p will vary from 0 to 1.00 depending on the value of your sample mean

p only equates α at the critical value

Directional Conditions (1)

You must have some expectation that the difference will fall in one direction and not the other

Directional Conditions (2)

You must have zero interest in the outcome if it should end up in the opposite direction

Why do you Never Say “Accept the Null”

States there is no relationsip between your variables of interest in the population

To say that you assert the null is a true statement

“Failed to Reject the Null” Acknowledges

That you don’t know why you didn’t reject the null

Type I Error

You rejected the null when it was true

Declaring there to be an effet when there isn’t one

False positive

Type II Error

Failing to reject the null hypothesis when the null hypothesis is false

When someone claims there is no difference but there actually is a difference

False negative

Between Subjects

Participants are only exposed to one level of the IV - they only experience one variable of the IV

Conditions you Would Use a T-Test

Your IV us between subjects and categorical

Your IV has exactly two levels

Your DV is continious and quantitative - at least on the interval scale

Assumptions of the T-Test

Your samples are independently and randomly selected from their population

Scores on the DV are normally distributed in the population

Homogeneity of Variance

Homogeneity of Variance

The variablity of the scores in the first group are equivilant to the variablity of scores in the second group

SS

Sums of squares - the SD from the mean

n

The number of scores in one subgroup

N

Total number of scores in all groups combined

Always refers to your total sample size

How do you Make the T Formula Bigger

Increase the numerator

Decrease the dominator

Between Group Variability

The extent to which your group means are fluctuating (i.e., differ from one another) 

Within Group Variability

The extent to which individual participant scores within each group are fluctuating

n2 Equation

SS Total = SS Between + SS Within

n2 equation (2)

SSbetween over SStotal

Computational Formula for N2

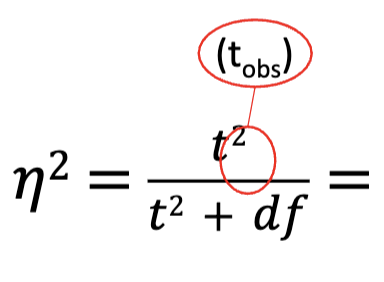
Rule of Thumb for N2

Weak: .05 

Moderate: .10 

Strong: .15 

Three Questions (1)

Is there an effect?

• Compare tobs and tcrit if t > tcrit reject Ho, there is an effect

Three Questions (2)

What is the nature of the effect?

• Which group scored higher on the DV? - Eyeball the means. The mean of group 2 was higher than the mean of group 1

Three Questions (3)

How strong was the effect?

• n2

Why is it n-2

There is one place in the dataset that is not free to vary

BGV Graph

How far apart or close the center point of 1 and 2 are

WGV Graph

How wide are the graphs

SSwithin

SS1 + SS2