STAT 201 MT 1 code

3, 4

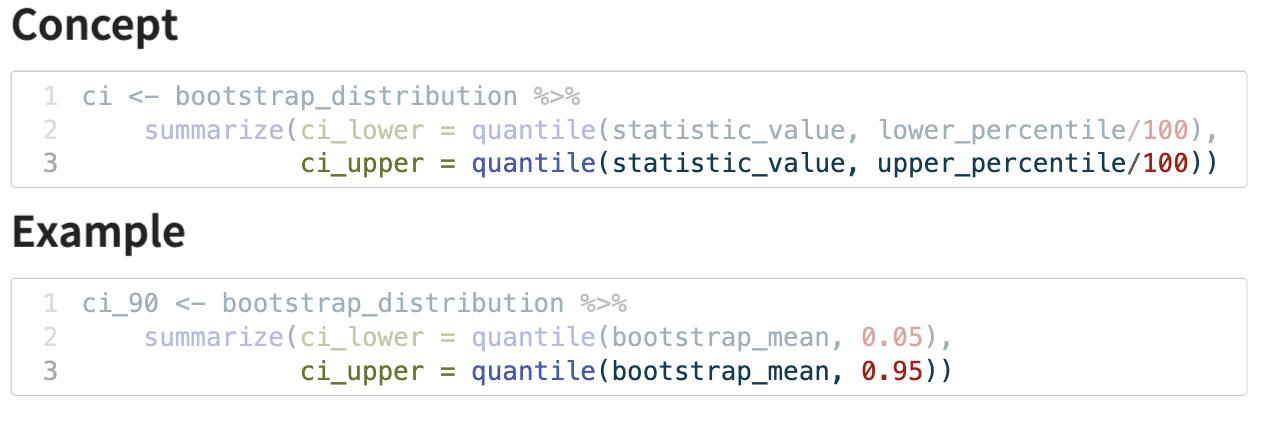
calculating the CI from a bootstrap distribution

plotting a CI on a bootstrap distribution

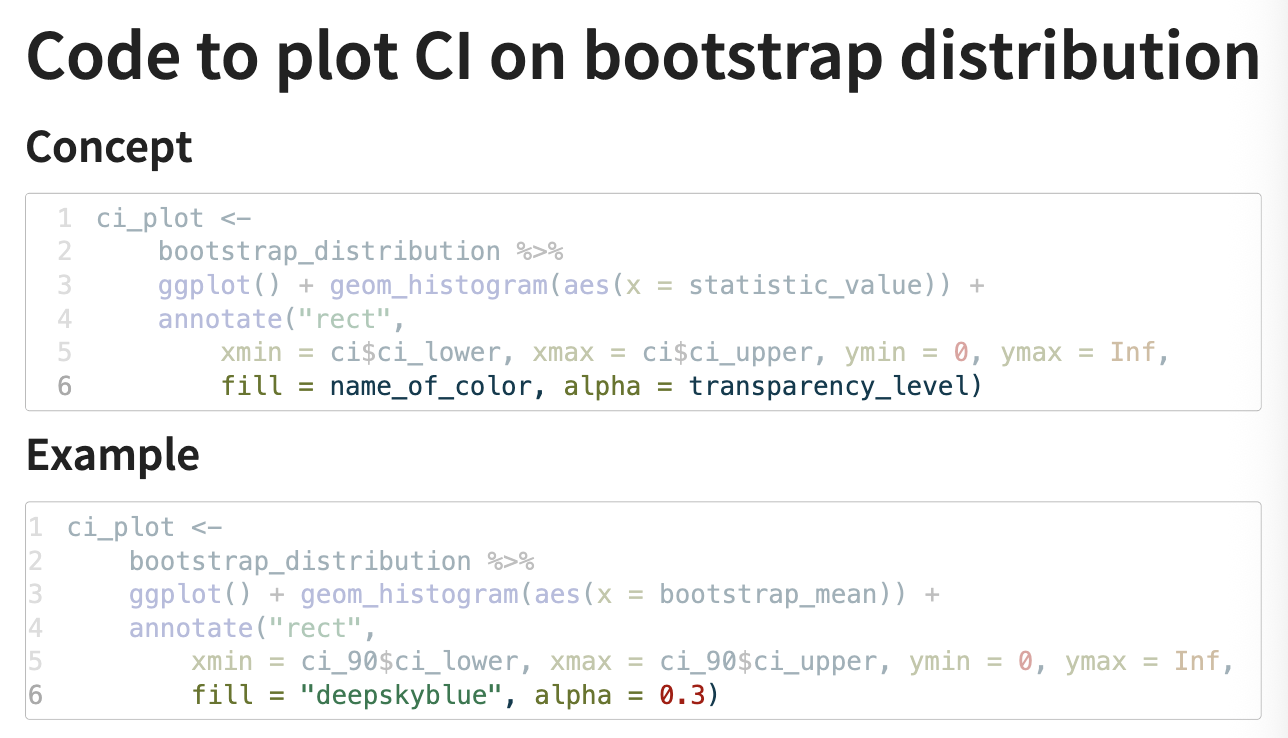
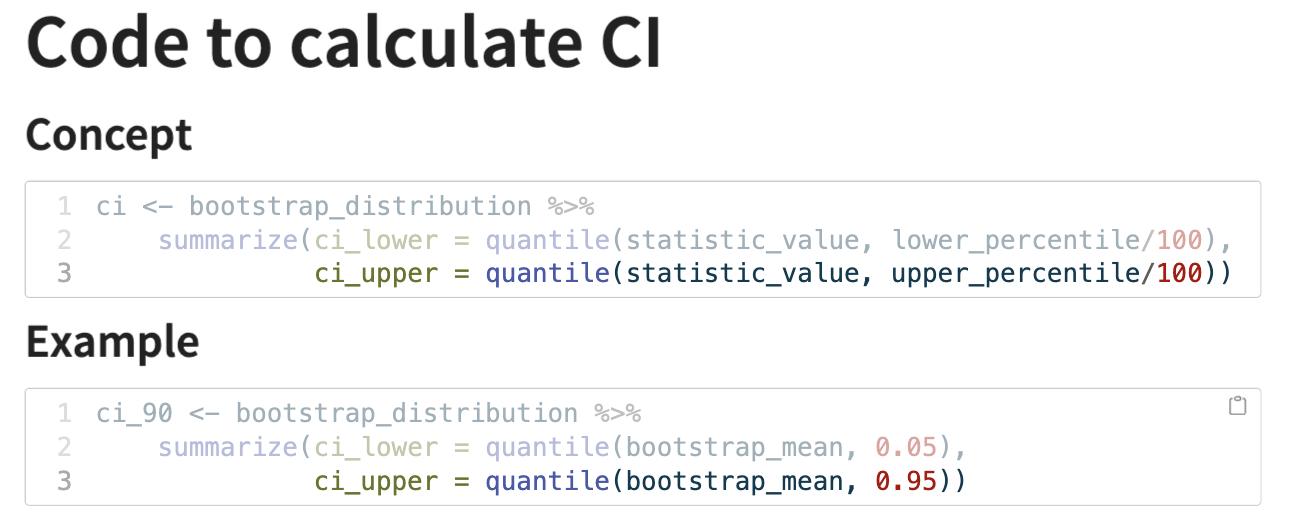
quantile()

used to calculate quantiles of a dataset; returns data points that divides the data set into equal sized groups

syntax:

quantile(x, prob)

x = a numeric vector containing your data

probs = a numeric vector of probabilities (0-1) for which you want to find the quantiles

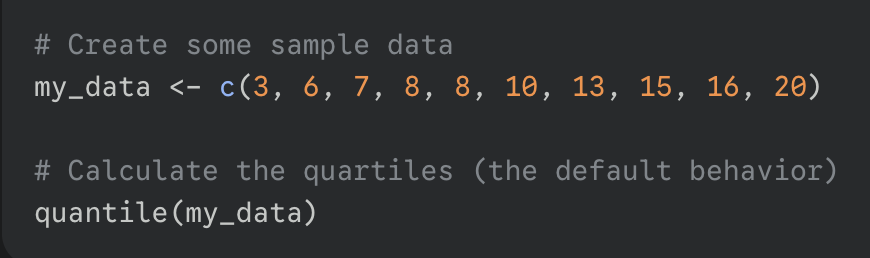
*if you do not specify the probs argument, R will calculate the quartiles by default; 0, 25, 75, 100

code for the normal approximation of sampling distribution 

(this is for the sampling distribution of means, in this case sd = sigma/sqrt(n))

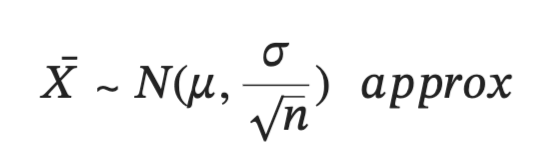
plotting the normal distribution/bell curve

• geom_line : specifies that we want to add a line

• data = tibble() : instead of using a pre-existing data frame, this code creates the data for the line (on the fly) using the tibble() function; this tibble has two columns:

  • values: a sequence of numbers that will serve as the x-coordinates for the curve 

  • density: calculates the corresponding y-coordinate for each value in the values column

• dnorm(…) : calculates the height (probability density) of the normal distribution curve for each point in values

• aes(values, density) : aesthetic mapping that tells geom_line() which columns to use for the plot: map the values column to the x-axis and the density column to the y-axis

*in short the code generates a series of (x, y) coordinates for a perfect normal curve with a specific mean and standard deviation and then connects them with a line to visualize the curve

qnorm()

calculates the quantile function for the normal distribution; give qnoem a probability (value between 0 and 1) and it gives back the corresponding z-score (the value on the x-axis of a standard normal curve)

density vs frequency

use frequency (the default) to see how many observations are in each bin

use density to see the shape of the distribution and to compare it to a theoretical probability distribution

• when using density (eg. freq = FALSE) the y-axis is rescaled so that the total area of all the bars in the histogram equals 1