Graph Theory Basics

Vertices

• Definition: Points in a graph where edges meet.

• Example: Think of them like intersections in a road network. They represent the entities or objects being connected.

Edges

• Definition: Line segments or curves that connect pairs of vertices.

• Example: Imagine them as the roads connecting intersections.

Loops

• Definition: Edges that start and end at the same vertex.

• Example: A loop could be a cul-de-sac that circles back to the same intersection.

A cul-de-sac is a dead-end street with only one way in and out. It typically ends in a rounded area or a loop that allows vehicles to turn around. These are often found in residential neighborhoods and can provide a quieter, safer environment for homes since there's no through traffic.

Think of it as a street that ends in a circle, creating a little enclosed community.

Graph Theory

• Definition: A branch of mathematics focused on the properties of graphs and their applications in solving real-world problems.

• Example: It’s used for finding the shortest path in networks, like routing a delivery truck efficiently.

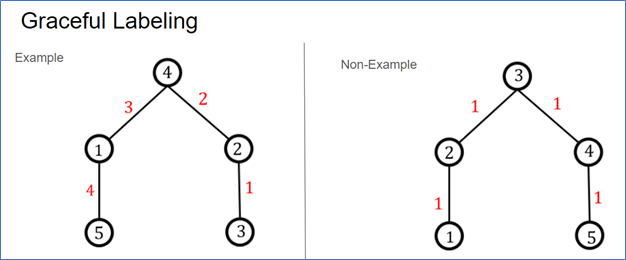
Vertices

What is 5 1 4 2 and 3?

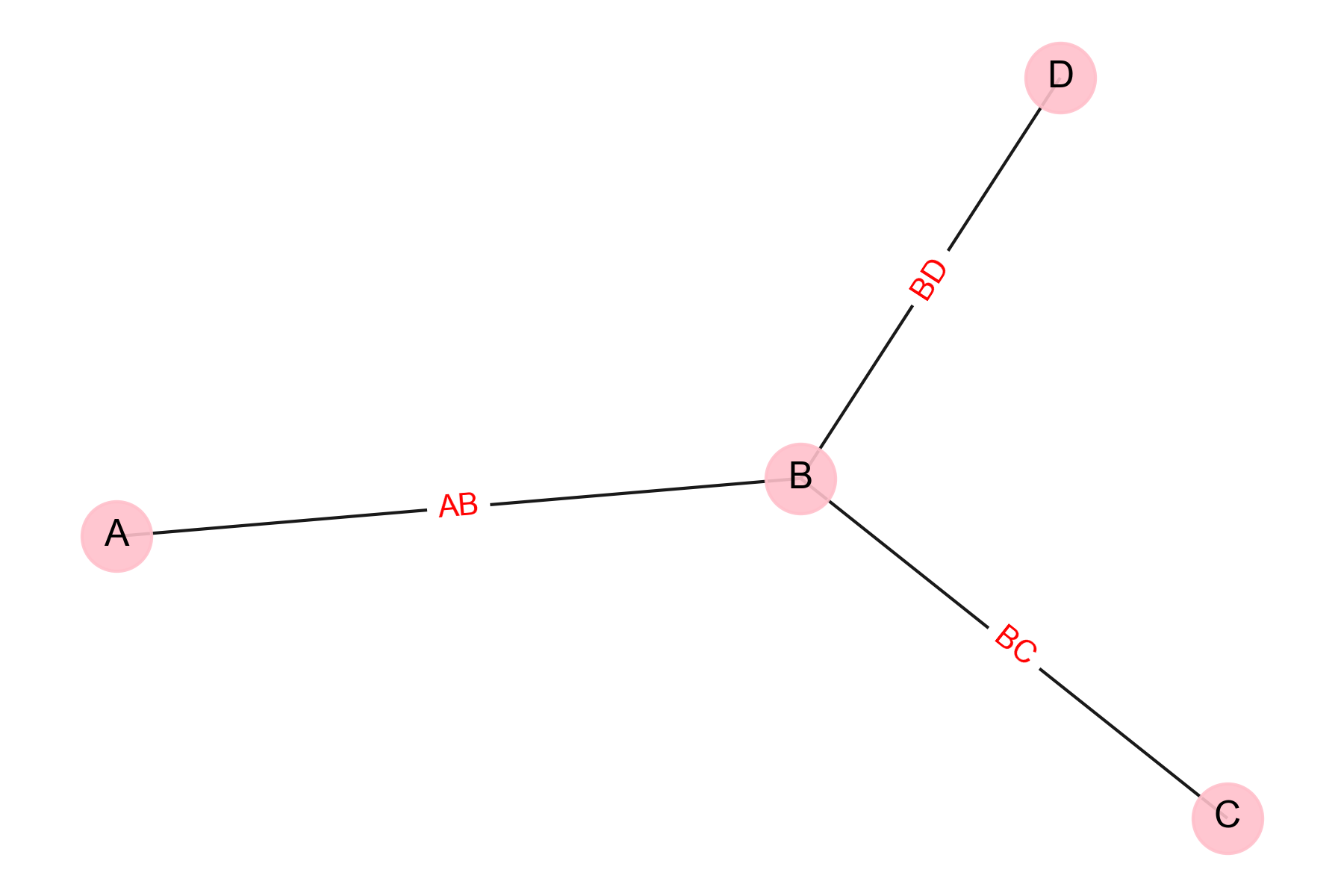
Edges

What is AB BD BC?

Equivalent

In graph theory, two graphs are considered equivalent if they have the same structure, meaning there is a one-to-one correspondence between their vertices and edges that preserves the connections.

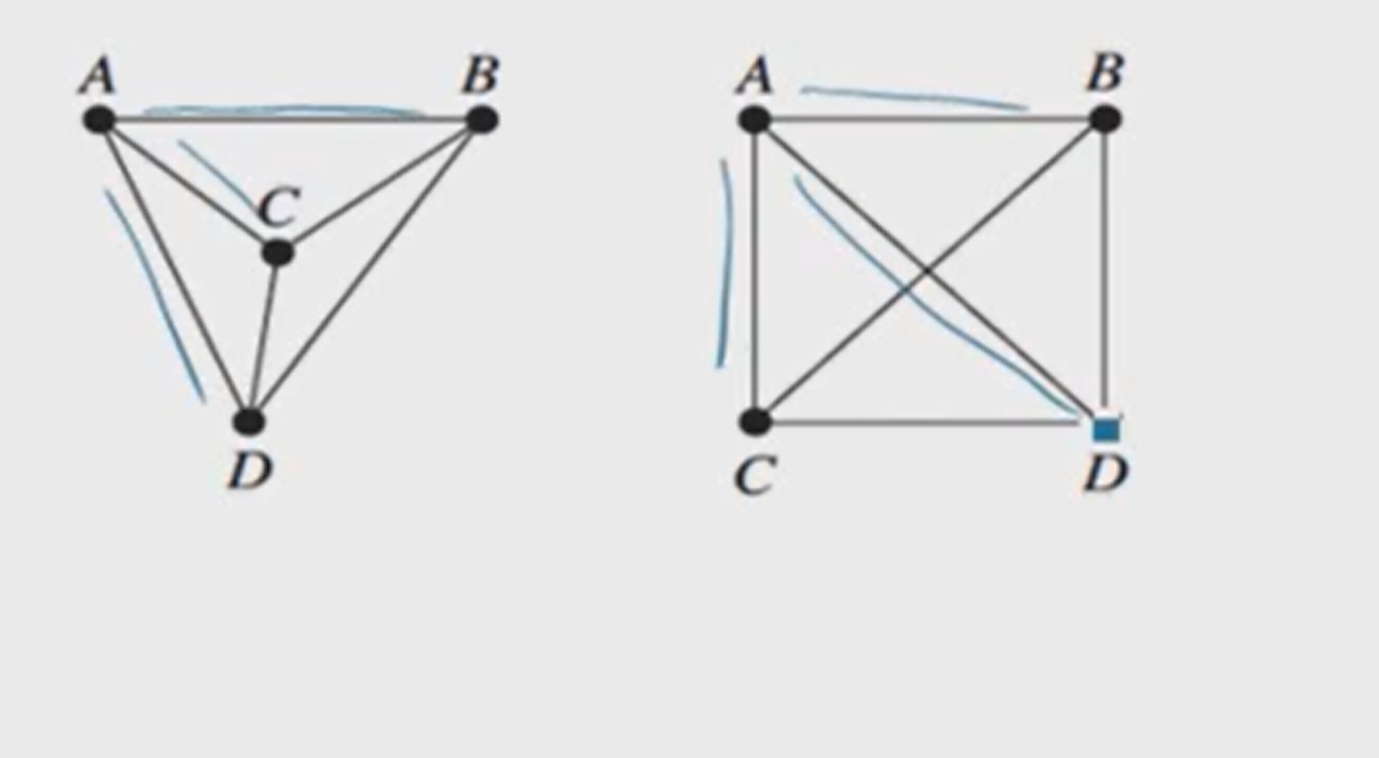
IS These drawings are considered equivalent?

Yes. Because the pattern of connections is identical, just with different names.

it's all about having the same pattern of connections between the same points (vertices) with the same connections (edges). So, if you have two graphs where the points are connected in the exact same way, just with different labels, those graphs are considered equivalent.