Informatik

Welche Laufzeit hat Selectionsort/ Minsort, ist der Algorithmus in Place oder stabil?

In allen Cases O(n²) , in place, nicht stabil.

Welche Laufzeit hat Insertionsort, ist der Algorithmus in Place oder stabil?

Die Laufzeit von Insertionsort beträgt im besten Fall O(n), im durchschnittlichen und schlechtesten Fall O(n²). Der Algorithmus ist in-place und stabil.

Welche Laufzeit hat Quicksort, ist der Algorithmus in Place oder stabil?

Die Laufzeit von Quicksort beträgt im besten Fall O(n log n), im durchschnittlichen Fall O(n log n) und im schlechtesten Fall O(n²). Durch randomieiserung des Pivot-Elements im Worst-Case : (n* logn). Der Algorithmus ist in-place (wenn Trick angewendet), aber nicht stabil.

Mergesort

Die Laufzeit von Mergesort beträgt im besten, durchschnittlichen und schlechtesten Fall O(n log n). Der Algorithmus ist nicht in-place, aber stabil.

Heapsort

Die Laufzeit von Heapsort beträgt im besten, durchschnittlichen und schlechtesten Fall O(n log n). Der Algorithmus ist in-place, aber nicht stabil.

Definition stabiler Sortieralgorithmen. Wie können nicht stabile Algorithmen stabil gemacht werden?

Ein stabiler Sortieralgorithmus bewahrt die relative Reihenfolge von gleichen Elementen im sortierten Ergebnis. Das bedeutet, dass bei gleichwertigen Einträgen deren ursprüngliche Reihenfolge erhalten bleibt. Nicht stabile Algorithmen können stabil gemacht werden, indem man zusätzliche Information zu den Elementen hinzufügt, z. B. durch Einfügen eines Indexwertes, oder durch die Verwendung von stabilen Sortieralgorithmen wie Mergesort als Teil des Verfahrens → Schlüssel

Definition in-place Sortieren

Ein in-place Sortieralgorithmus sortiert die Daten in der gleichen Speichernutzung, ohne zusätzlichen Speicherplatz für die Sortierung zu benötigen.

Welcher Laufzeit entspricht (n-1) + (n-2) + (n-3) + …+ 2+ 1

= (n-1)*n/ 2 = n²/2-n/2 → O(n²)

Wie funktioniert Quicksort?

Quicksort ist ein schneller Sortieralgorithmus, der die Auswahl eines Pivot-Elements verwendet, um die Liste in zwei Partitionen zu teilen. Elemente, die kleiner als das Pivot sind, werden links und größere rechts angeordnet, gefolgt von rekursivem Anwenden des gleichen Verfahrens auf die Teilmengen.

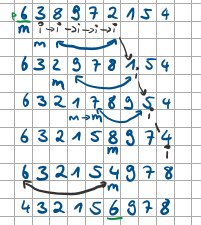
Wie funktioniert Mergesort?

Mergesort ist ein stabiler Sortieralgorithmus, der die Liste in zwei Hälften teilt und dann jede Hälfte rekursiv sortiert, bevor die beiden sortierten Hälften zusammengeführt werden. Nachteil: viel Speicherplatz benötigt.

Wie funktioniert Heapsort?

Heapsort erstellt zunächst einen Min-Heap aus einer Liste mit der Laufzeit O(n), heapify_up/down (O(ldn). Zum sortieren der Liste wird dann je das Minimum aus der Wurzel extrahiert → konstant O(1) mit heapify_down (O(ldn).

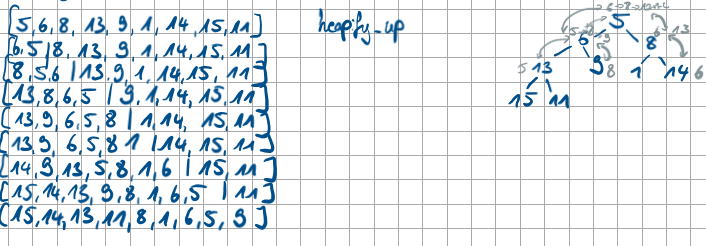
Was sind dynamische Datenstrukturen?

• dynamisch wachsend und schrumpfend, in Heap abgelegt

• besitzen Zeiger: Werte, die auf Speicheradresse anderer Werte zeigen.

• in Python realisiert durch Listen, Klassen und Dictionaries

Wie sieht eine Implementierung von dynamischen Datenstrukturen in Listen aus?

list= [42, [73, [[[[…, None]]]]] → Verknüpft. Jede Liste hat aber die Länge 2

Wie sieht eine Implementierung von dynamischen Datenstrukturen in Klassen aus?

class Node:

def __init__(self):

self.value= value

self.next= None

def update_next(self, new_next):

self.next= new_next

Wie sieht eine Implementierung von dynamischen Datenstrukturen in Dictionaries aus?

dict= {“value: 42, “next”: {“value: 73, “next:None}}

second [“next”]= dict

Was sind Stacks, welchem Prinzip folgen sie?

Dynamische Datenstruktur, die auch als Kellerstruktur bezeichnet werden. Im Stack kann immer nur auf das neuste Element zugegriffen werden. Werte werden in bestimmter Reihenfolge gespeichert.

LIFO: last in first out

Welche Operationen können auf einen Stack angewendet werden?

1. s= empty_stack() → erstellt leeren Stack

2. push(s, value) → fügt Wert hinzu “oben rauf”

3. top(s, value) → gibt obersten Wert zurück

4. last= pop(s, value) → entfernt obersten Wert, kann zudem gespeichert werden (last)

Was ist eine Queue?

Die Warteschlange ist eine dynamische Datenstruktur. Sie speichert wie ein Stack Werte in der zugefügten Reihenfolge. Anders als im Stack gilt hier das FIFO Prinzip: First in first out.

Welche Operationen können auf eine Queue angewendet werden?

1. q= empty_queue→ konstruiert leere Queue

2. enqueue(s, value) → fügt Wert hinzu “oben rauf”

3. top(s, value) → gibt obersten Wert zurück

4. first= deque(s, value) → entfernt untersten Wert, kann zudem gespeichert werden (first)

Welche Elemente und Eigenschaften hat ein Baum?

Verzweigung: Knoten

Knoten ohne Kinder: Blätter

Verzweigungsgrad: Anzahl möglicher Kinder (Binärbaum: 2 oder 0)

Höhe: maximales Vorkommen innerer Knoten auf Pfad von Wurzel zu empty_Wert. (Aus 3 werten bestehender Baum → 2 gefüllte Level: Höhe 2)

Blätter: 2^h mit h: Höhe. 2^0= 1Blatt → Wutzel auch Blatt, 2^1 = 2 Blätter, 2² = 4 Blätter, …

Wie ist ein Suchbaum aufgebaut? Wie funktioniert das Nachschlagen und Einfügen von Werten?

Für jeden Knoten im Baum gilt: Wert im Knoten > alle Werte im linken Teilbaum und < als alle im rechten Teilbaum.

Nachschlagen: Pfad kann Weg angeben, ob nach links oder rechts “abgebogen” werden muss. genauso kann überprüft werden, ob der gesuchte Wert kleiner (links) oder größer (rechts) oder gleich der Wurzel ist. Wird ein empty-Wert erreicht, ist der gesuchte Wert nicht im Suchbaum enthalten. Einfügen funktioniert gleich. Bei gleichen Werten wird der Wert nicht eingefügt. Beim erreichen des Empty-Wertes, kann der Wert an dessen Position eingefügt werden.

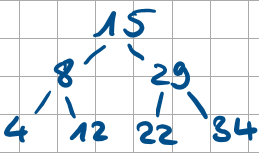
Laufzeiten in einem Suchbaum. (Nachschlagen, Löschen)

Nachschlagen: Best-case, Average-Case O(ldn)/ O(Höhe) mit n der Elemente im Baum. Worst-Case: O(n) bei einseitigen Bäumen.

Löschen: 1. Nachschlagen des Wertes. Dann ersetzten durch Kind, falls dieses nur 0-1 Kinder hat. Ansonsten Suchen des linken höchsten Wertes oder rechten kleinsten Wert und ersetzten durch diesen.→ O(h) mit Worst-Case O(n)

Welche Operationen können durch das Balancieren des Baums (AVL) verbessert werden?

find/ min/max (→ O(h) bis O(n) zu O(logn)),

insert & delete (→ O(h) bis O(n) zu O(logn)),

Wie ist die Balance eines Teilbaums auszurechnen? Wann werden diese provoziert?

balance(tree)= height(tree.right) - height(tree.left)

Provoziert durch hinzufügen oder Löschen von Werten.

Bei welchen Balancen werden welche Rotationen ausgeübt. Male die Bäume für eine L-, R-, LR-, RL-Rotation auf.

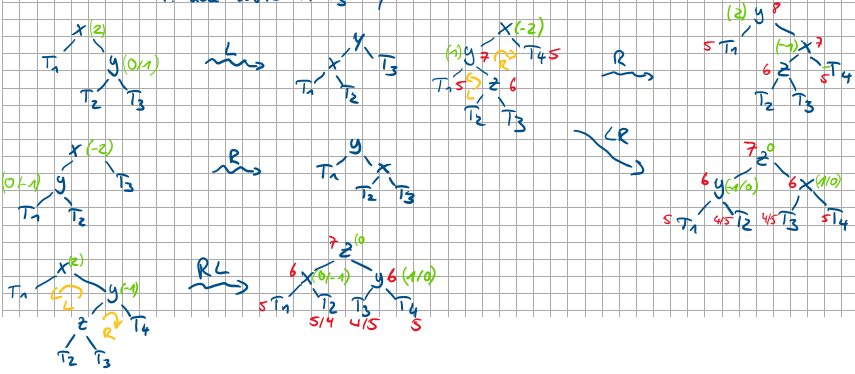
Welche Balance und Höhe hat der Baum nach einer Rotation?

Höhe des neuen Baumes: h-1, Balance 0,1 oder -1

Was ist eine priority queue Prioritätswarteschlange?

Prioritätswarteschlange: abstrakte Datenstruktur (ADT)

Queue + Priorität (falls gleiche Werte: nacheinander in der Queue).

• insert(x, p) → füge ein Element xxx mit Priorität ppp ein

• find-min / find-max → finde das Element mit höchster Priorität

• delete-min / delete-max → entferne das Element mit höchster Priorität

Wie kann eine Prioritätswarteschlange (ADT) in einer Baumstruktur dargestellt werden?

In Heaps dargestellt. Prioritäten werden als Knoten gespeichert. MinHeap hat kleinste Prio als Wurzel. Neben den Prioritäten können dann Values abgespeichert werden.

Wie können bei der Listendarstellung eines Heaps auf die Kinderknoten und die Elternknoten zugegriffen werden mit der Nutzung vom Index des auszugehenden Wertes i?

Elternknoten: (i-1)//2

linker Kindknoten: i*2+1

rechter Kindknoten: i*2+2

minimum Index 0,

Was heißt amortisierte Laufzeit

Durch Speicherverschwendung erkaufte konstante Laufzeit.

amortisierte Kosten= Gesamtkosten der n Operationen/ n

Verdopplung von Speicher nachdem Speicher voll ist, lässt n konstante Operationen zu (O(1)), bis eine in O(n) kommt. dadurch so gut wie Konstant.

Was sind Arrays? besondere Eigenschaften

Datenstruktur mit fester Länge, keine heterogene Elemente, jedes Element über Index erreichbar.

lesen& schreiben in konstanter Laufzeit., NICHT dynamisch!

Male auf, wie ein Array gespeichert ist.

Was passiert, wenn man einen Wert an einen Array zufügen will? Und Lösung für Problem.

append fügt ans Ende hinzu, Speicherplatz hinter array ende kann schon belegt sein → neuen größeren Speicherplatz reservieren und Array-Werte kopieren.

Problem: wenn mehrere Variablen auf Array verweisen, müssen alle Speicheradressen aktualisiert werden

LÖSUNG: Zusätzlicher Verweis zwischen Variablen und Listen. feste Adresse zeigt auf Zeiger, der die Speicheradresse des Arrays zeigt. Die feste Adresse nicht änderbar aber der Zeiger wird aktualisiert, falls die Speicheradresse geändert wird. Variable → Zeiger → Speicherblock

sind absolute Laufzeiten oder die Steigung des Wachstums bei steigender Eingabe interessanter?

Steigung

Was sagen die Symbole aus: g(n) = O(f), Ω(f), o(f), ω(f), Θ(f)?

• O: obere Schranke (≤ mit einem Faktor). g wächst höchstens so schnell wie f

• Ω: untere Schranke (≥ mit einem Faktor). g wächst mindestens so schnell wie f

• o: echt kleiner. g wächst stets langsamer als f

• ω: echt größer. g wächst stets schneller als f

• Θ: gleich groß (oben und unten gleichzeitig beschränkt).

Was bedeuten die einzelnen Teile dieser Schreibweise?

O(f)={g: N→R+ ∣ ∃C > 0 ∃n0 ​∈ N ∀n ≥ n0​: g(n) ≤ C⋅f(n)}.

• N→R+
  bedeutet: g ist eine Funktion von den natürlichen Zahlen zu den positiven reellen Zahlen.

• ∃C>0 („Es existiert ein C>0“): ein fester Faktor.

• ∃n0 ​∈ N („Es existiert ein n0 in den natürlichen Zahlen“): ab einer bestimmten Startschwelle.

  ∃: Existenzquantor: ‘es gibt’

• ∀n ≥ n0​ („Für alle n≥n0 ​ gilt ...“): Bedingung gilt ab dieser Schwelle für alle größeren n.

  ∀: Allquantor: ‘für alle’

• ​g(n) ≤ C⋅f(n) das ist die eigentliche Ungleichung: g wächst höchstens so schnell wie f, bis auf den konstanten Faktor C.

Mit welchem C und n0 kann g ∈ O(f) sein:

bringe die Laufzeiten in aufsteigende Reihenfolge:

O(1) < O(logn) < O(n) < O(n logn) < O(n²) < O(n³) < O(2^n) < O(3^n) < O(n)! < O(n^n)

O(1) < O(logn) < O(n) < O(n logn) < O(n²) < O(n³) < O(2^n) < O(3^n) < O(n!) < O(n^n)

Wie wird eine Laufzeit bewiesen?

Durch den Satz von l’ Hôspital:

lim f’(n)/ g’(n) = lim f(n)/g(n) darf angewendet werden, wenn 0/0 oder ∞/∞ vorliegt.

Zeige, dass g ∈ o(f) gilt.

g(n) = ld(n)², f(n) = n*ld(n)

g(n)/f(n) = ld(n)²/ n*ld(n) = ld(n)/n = ln(n)/ln(2)*n

Ableitung beider therme einzeln: 1/ln(2)*n

mit n → ∞: lim= 0 Damit ist die Aussage bewiesen

Male die verschiedenen Landau-Notationen auf in einem Diagramm, aus dem die Abhängigkeit hervorgeht

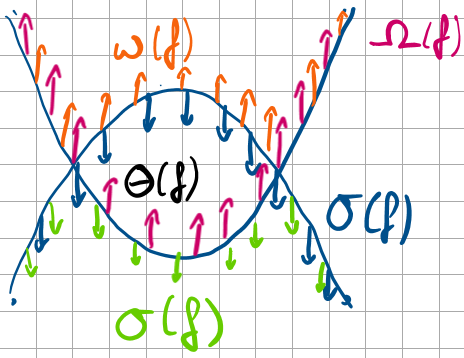
Zu welchem Symbol gehören die beiden Schreibweisen:

{g: N→R+ ∣ ∃C > 0 ∃n0 ​∈ N ∀n ≥ n0​: g(n) ≥ C⋅f(n)}

{g: N→R+ ∣ ∀C > 0 ∃n0 ​∈ N ∀n ≥ n0​: g(n) ≥ C⋅f(n)}

1. Ω

2. ω

Was entspricht 1. lim​_n→∞ g(n)/n(n)​ <∞

2. lim​_n→∞ g(n)/f(n)​=0

3. lim​_n→∞ g(n)/f(n)​=k

1. g∈O(f), f∈Ω(g)

2. g∈o(f), f∈ω(g)

3. g∈Θ(f), f∈Θ(g)

Wie ist die Proportionalität der Kanten zu den Knoten in einem gerichtetem Graph (Einbahnstraßen) ausgegangen wird.

E ⊂ V1 x V2 mit V1: Ausgangsknoten, V2: Zielknoten, Kantenmenge ⊂ ist Teilmenge der Knotenpaar-Menge. Alle Kanten verbinden nur Knoten aus V miteinander. Jedes Element von VxV ist ein Paar von Knoten.

bei ungerichteten Graphen: Reihenfolge wichtig.

→ aus VxV= {(u,v) | u ∈ V, v ∈ V} wird {{n,m} | n,m ∈ V}

Male die Adjazenzmatrix von [FL, KI, NMS, HL, HH], Fl: 60 NMS, 70 KI; 1KI: 30 NMS, 80HL; NMS: 50HL, 60HH; HL: 70HH

0 1 2 3 4

0 0 70 60 ∞ ∞

1 70 0 30 80 ∞

2 60 30 0 50 60

3 ∞ 80 50 0 70

4 ∞ ∞ 60 70 0

Was sind Unterschiede in der Tiefen und der Breitensuche? → Datenstruktur, Besuchte Knoten, Pfadlänge, Speicherbedarf, Anwendung

Eigenschaft	DFS	BFS

Datenstruktur

Stack / Rekursion

Queue

Besucht Knoten

„tief“ in einen Zweig

„flach“ schichtweise

Pfadlänge

Nicht garantiert kürzester Pfad

Garantiert kürzester Pfad in ungewichteten Graphen

Speicherbedarf

O(V) Rekursionstiefe (bei Baum)

O(V) max. Breite der Ebene

Anwendung

Topologische Sortierung, Zyklenprüfung, Pfadsuche

Kürzeste Wege, Level-Bestimmung, Netzwerkflussvorbereitung

Backtracking. Ausgelassen für jetzt

Was ist dynamisches Programmieren?

Dynamisches Programmieren ist eine Optimierungstechnik, um Probleme zu lösen, die überlappende Teilprobleme haben und eine optimale Teilstruktur besitzen.

• Überlappende Teilprobleme: Das Problem kann in Teilprobleme zerlegt werden, die mehrfach auftreten.

• Optimale Teilstruktur: Die optimale Lösung des Gesamtproblems kann aus den optimalen Lösungen der Teilprobleme aufgebaut werden.

DP vermeidet Rekursionen mit doppelter Arbeit, indem Teillösungen gespeichert werden.

Welche Operationen können bei der Editierdistanz von zwei Wörtern genutzt werden?

Delete (i)

Insert (i, a)

Replace (i,a)

as ist die Editiersequenz? Wie kann diese aussehen?

Die Abfolge von Operationen, die aus einem Wort das andere macht. DEL(1); REP(2,S)

Was ist die Editierdistanz?

Die Anzahl an Operationen, die mindestens ausgeführt werden müssen.

Warum normalisiert man die Operatoren? Bei welchen 4 Editier-Operationen ist die Reihenfolge entscheidend? ( j < i )

Normalisierung, um die Operatoren seriell über beide Wörter nutzen zu können.

DEL(i); DEL(j) wird zu DEL(j); DEL(i) REP(i,a);

DEL(j) wird zu DEL(j); REP(i − 1,a)

DEL(i); INS(j,a) wird zu INS(j,a); DEL(i + 1)

INS(i,a); INS(j,a) wird zu INS(j,a); INS(i + 1,a)

Wie ist die Laufzeit der Ermittlung der (kleinsten) Editierdistanz naiv also ohne Memorization

Laufzeitanalyse naiv

• Jeder Aufruf mit (m,n)) erzeugt bis zu 3 rekursive Aufrufe (Insert, Delete, Replace).

• Rekursionstiefe ist höchstens m+n.

• Anzahl Knoten im Rekursionsbaum: im Worst Case O(3^m+n).

T_naiv(m,n) = O(3^m+n) Exponentiell, weil dieselben Teilprobleme immer wieder berechnet werden.

Wie kann die Editierdistanz effektiver ermittelt werden? Mit welcher anderen Funktion/Berechnung wird diese Methode verglichen?

Wie bei Fibonacci wird bei der naiven Variante Teilprobleme immer wieder aufgerufen → exponentiell.

D(i, j) hängt ab von D(i−1, j), D(i, j−1), D(i−1, j−1). Die selben Teilprobleme tauchen auch hier öfter auf → Memoization/DP, damit jedes Teilproblem nur 1x berechnet wird.

Im Gegensatz zu Fibonacci (O(n)) ist die Laufzeit hier =(m*n). Also abhängig von beiden Wortlängen.

Bsp.

D(2,2) ( "ab" vs "cd" )

├─ D(1,2) ( "a" vs "cd" )

│ ├─ D(0,2) (" " vs "cd")

│ └─ D(1,1) ("a" vs "c")

│ ├─ D(0,1)

│ ├─ D(1,0)

│ └─ D(0,0)

├─ D(2,1) ( "ab" vs "c" )

│ ├─ D(1,1) (kommt nochmal!)

│ └─ D(2,0)

└─ D(1,1) ( "a" vs "c" ) (kommt nochmal!)

Was ist das Grundkonzept und Ziel vom Hashing?

Umwandeln von Daten beliebiger Größe in einen kurzen Index → Hashwert oder Schlüssel

Zeiel: Schnelles Suchen, Einfügen, Löschen und Prüfen, ob Element existiert O(1)

Mit welchen Datenstrukturen kann Hashing in Python umgesetzt werden.

Liste von Paaren, Suchbäume, Dictionaries

Welche Probleme können bei der Erstellung des Hashwertes auftauchen?

Die Hashfunktion kann so programmiert sein, dass bspw. Strings mit gleichen Buchstaben den gleichen Wert zugewiesen bekommen. Entweder können die Werte dann überschrieben werden oder es wird eine Liste angelegt mit beiden Strings. Sind zu viele Eingaben in der Liste, ist Array nur noch um konstanten Faktor effizienter. (Dominanz der inneren Listenstrukturen)

→ dynamischer Array, der bei best. Füllgrad vergrößert wird. Mit amortisierter Laufzeit.

→ großer Schlüsselbereich/ KeySet {0,1,…., n-1}

Was ist ein Bit (b), Byte (B)?

Bit: kleinste Informationseinheit: 0 oder 1

Byte: 8 Bit: ein Zeichen hat 1 Byte. Nutzung bspw. bei ASCII-Zeichen.

Nenne ein Beispiel für verlusthafte und verlustfreie Datenkompression

verlusthaft: jpeg, mp4

verlustfrei: zip

Was beschreibt der Begriff Entropie?

Informationsdichte

Bei geringer Informationsdichte, viele Werte unnötig → kompakte Darstellunf mögl.

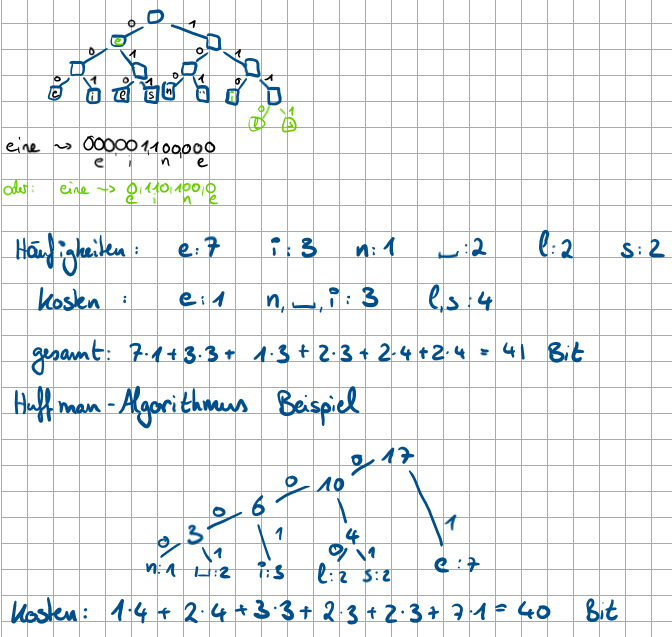
Wie viele Zeichen benötigt man, um “eine leise eselei” darzustellen, wie viele Bits ?

8×17 Zeichen → 144 Bit

6 Zeichen: (e, i, n, _, l, s) → 8 Bit code: 8×17 = 144 Bit

aber 6 Zeichen auch als 3 Bit code darstellbar → 3×17= 51 Bit

Wie sähe der Huffman-Algorithmus für “eine leise eselei” aus?