AP Precalc Midterm

The table gives values for a polynomial function f at selected values of x. What is the average rate of change of f over the closed interval [1,4]?

A. -2

The average rate of change over the closed interval [1,4] is the slope of the secant line from the point (1,16) to (4,10).

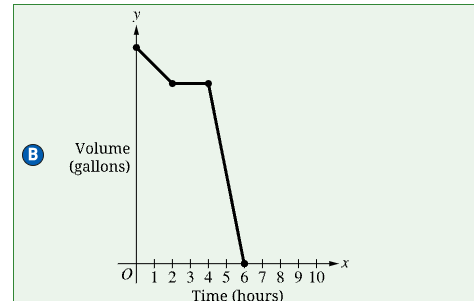
The figure shows a swimming pool filled with water. A pump is used to remove water from the pool until the pool is empty. When the pump is running, the rate at which the volume of water in the pool decreases is constant. During the first two hours, the pump works slower than usual due to a broken piece. Then the pump stops working. The broken piece is replaced, and the pump works at its usual rate until the pool is completely emptied of water. The entire process of emptying the pool takes six hours. Which of the following graphs could depict this situation, where time, in hours, is the independent variable, and the volume of water in the pool, in gallons, is the dependent variable?

B.

This graph accurately depicts the verbal description of the emptying of the pool, taking into account the varying rates at which it emptied and the amount of time it emptied at each rate.

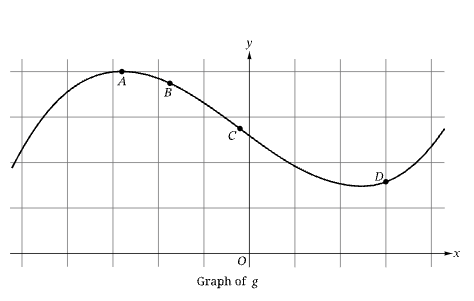
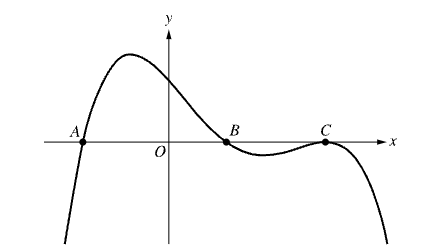
The figure shows the graph of a function g in the xy-plane with four labeled points. It is known that a relative maximum of g occurs at A, and the only point of inflection of the graph of g is C. Of the following points, at which is the rate of change of g the least?

C. C

The rate of change of g is least at the point of inflection C. The rate of change is negative at this point, and the graph is steeper at point C than it is at point B. The rate of change of g is changing from decreasing to increasing at point C.

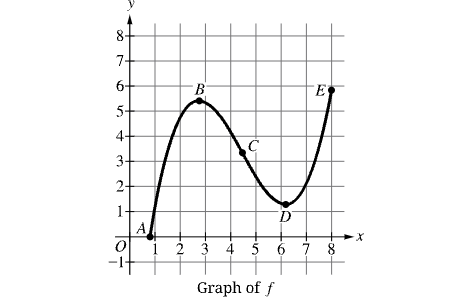
The figure shows the graph of a function f. The zero and extrema for f are labeled, and the point of inflection of the graph of f is labeled. Let A, B, C, D, and E represent the x-coordinates at those points. Of the following, on which interval is f increasing and the graph of f concave down?

A. the interval from A to B

The function is increasing, and the graph of the function is concave down on this interval.

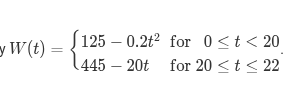
Consider the piecewise function W. Which of the following is a correct statement about the average rates of change of W ?

B. The average rate of change of W for 10≤t≤15 is less than the average rate of change of W for 5≤t≤10. 

W is quadratic, and the graph is concave down on 0<t<20. Therefore, the average rates of change over equal-length input-value intervals are decreasing as t increases. 

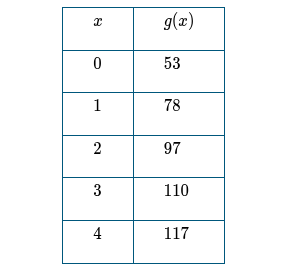
The table shows values for a function g at selected values of x. Which of the following claim and explanation statements best fits these data?

D. g is best modeled by a quadratic function, because the change in the average rates of change over consecutive equal-length input-value intervals is constant.

The average rates of change over equal-length input-value intervals of length 1 for function g are 25, 19, 13, and 7. The change in these average rates of change, the 2nd differences, is a constant  6. Therefore, a quadratic function (degree 2) best models the data in the table.

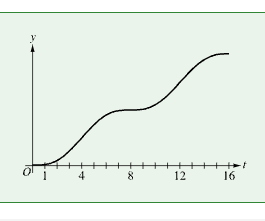
For 0≤t≤16, the rate at which customers arrive at a restaurant on a given day is modeled by the function R, where Rt is measured in customers per hour and t is measured in hours since the restaurant opened. The function R is increasing for 0<t<4 and 8<t<12, and R is decreasing for 4<t<8 and 12<t<16. The function N models the total number of customers who have arrived at the restaurant since it opened, up to time t. Which of the following could be the graph of y=Nt for 0≤t≤16?

D.

The rate at which customers arrive at the restaurant is increasing for 0<t<4 and 8<t<12 and decreasing for 4<t<8 and 12<t<16. Therefore, the graph of N is concave up on 0<t<4 and 8<t<12. The graph of N is concave down for 4<t<8 and 12<t<16. This graph meets all of these requirements for the graph of y=Nt. The total number of customers is increasing at an increasing rate on those intervals on which the graph of N is concave up. The total number of customers is increasing at a decreasing rate on those intervals on which the graph of N is concave down.

The polynomial function f is an odd function with domain -4≤x≤4. The table gives information about values of f(x) and the behavior of the function. What is the absolute maximum value of f on its domain?

B. 3

Because f is odd, the function is graphically symmetric about the point 0,0 and analytically has the property f(-x)=-f(x). Based on the table, the absolute minimum value is f(2)=-3. Therefore, the absolute maximum value is f(-2)=-f(2)=3.

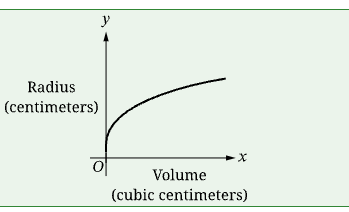
The figure shows a sphere that can expand. As it expands, the volume inside the sphere and the radius of the sphere both increase. In particular, the radius increases at a decreasing rate with respect to the volume.

Which of the following graphs could depict this situation, where volume, in cubic centimeters, is the independent variable and radius, in centimeters, is the dependent variable?

B.

In this graph, as the volume increases, the radius increases at a decreasing rate.

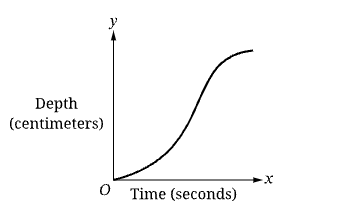
At time t=0, water begins pouring into an empty container at a constant rate. The water pours into the container until it is full. The situation is modeled by the given graph, where time, in seconds, is the independent variable and the depth of water in the container, in centimeters, is the dependent variable. For which of the following containers would the graph be appropriate?

B.

Because the diameter of the container decreases until the middle of the container, then increases, this container corresponds to the behavior shown in the graph. The graph is most steep in the middle portion of the graph with the relationship between the two quantities depth and time.

The function C models the cost, in dollars, for producing x items and is given by Cx=1000+bxx, where b is a constant. It is known that the cost is $115 to produce 10 items and $65 to produce 20 items. What is the average rate of change of C as x changes from x=30 to x=40 ?

A. $-0.83 per item

In function C, the value of b can be found by solving either 115=1000+b1010 or 65=1000+b2020. This results in b=15. Using Cx=1000+15xx, the average rate of change of C on 30,40 is C40-C3040-30=-$0.83 per item. The average rate of change can also be found without solving for b. If Cx=1000+bxx, then C40-C3040-30=1000+40b40-1000+30b3010, which simplifies to 3000+120b-4000-120b120·110=-10001200=-$0.83 per item.

The figure shows the graph of a quartic polynomial function with zeros at A, B, and C. Which of the following statements gives the multiplicity of the zero at C with correct reasoning?

C. 2, because the quartic polynomial function has three real zeros, one of which must have a multiplicity of 2, and the polynomial does not change signs at C.

A quartic polynomial has exactly 4 complex zeros when counting multiplicities. Because 3 of the real zeros are identified, the fourth zero must also be real. Non-real zeros occur in conjugate pairs. Therefore, one of the real zeros must have a multiplicity of 2. Because the graph is tangent to the x-axis at C, that zero has even multiplicity, which in this case means a multiplicity of 2.

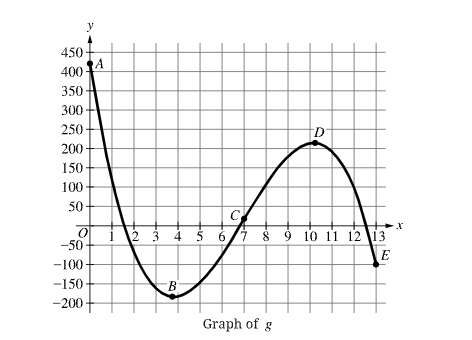
The figure shows the graph of function g for 0≤x≤13. The endpoints of the interval are labeled with points A and E. Two other extrema for g are labeled with points B and D. Point C is the only point of inflection of the graph of g for 0≤x≤13. Let tA, tB, tC, tD, and tE represent the x-coordinates at those points. Of the following, on which intervals is the rate of change of g decreasing?

D. [Tc, Td] and [Td, Te]

These are the intervals on which the graph of g is concave down because the rate of change of g is decreasing.

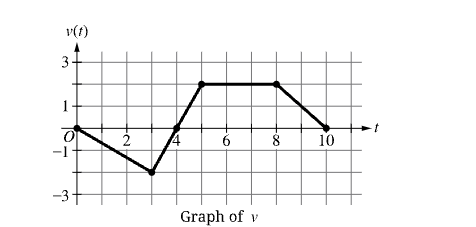
An object travels along a horizontal line with velocity given by the function v. The graph of y=vt, which consists of four line segments, is shown for 0≤t≤10. On which of the following intervals is the object’s velocity decreasing over the entire interval?

D. 0<t<3 and 8<t<1

A function is decreasing over an interval of its domain if, as the input values increase, the output values always decrease. That is, for all a and b in the interval, if a<b, then fa>fb. The velocity function is decreasing on both of these intervals.The object’s velocity is decreasing on the intervals where the graph of y=vt slopes downward consistently.

Let Q represent a mass of radioactive radium (226Ra) (in grams), whose half-life is 1599 years. The quantity of radium present after t years is Q = 5(1/2)^(t/1599). Determine the quantity present after 300 years. Round the answer to the nearest hundredth of a gram if necessary.

b. 4.39 g

Evaluate the function at the indicated value of x. Round your result to three decimal places.

h(x)=250e^0.05x, x=15

d. 529.250

Evaluate the function at the indicated value of x. Round your result to three decimal places.

f(x)=5^x, x=-π

c. 0.006

Evaluate the function at the indicated value of x=0.67. Round your result to three decimal places if necessary.

f(x)=5lnx

d. -2.002

Evaluate the logarithm using the change-of-base formula. Round your result to three decimal places.

log8(0.5)

a. -0.333

Evaluate f(x)=logx at the indicated value of x. Round your result to three decimal places.

x=21.5

b. 1.332

Determine the balance A for P dollars invested at rate r for t years and compounded monthly and compounded quarterly.

P=$1500; r=2%; t=10 years

Monthly: $1831.80

Quarterly: $1831.19

Use a graphing utility to construct a table of values for the function. Round your answers to three decimal places.

f(x)=e^4x

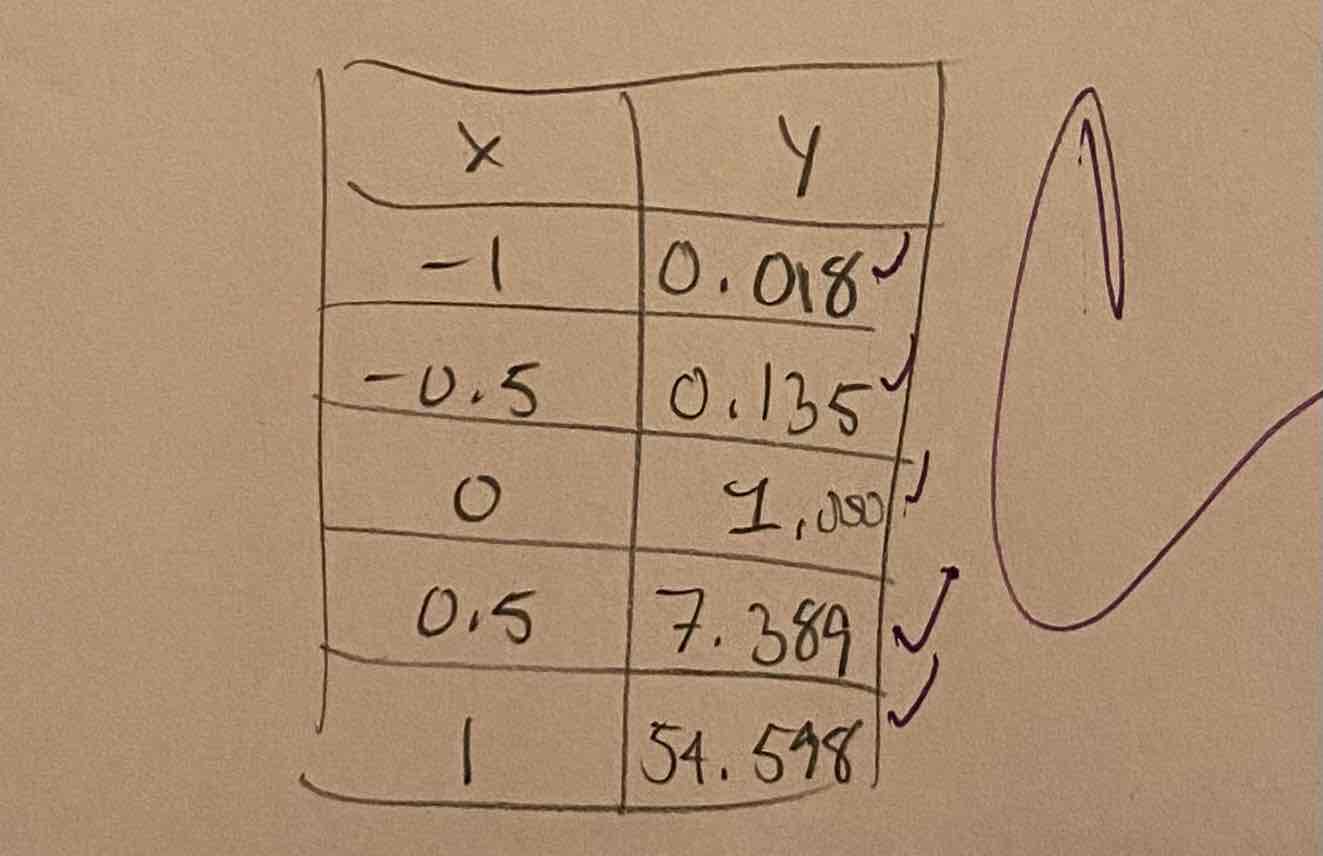
Use a graphing utility to construct a table of values for the function. Round your answers to two decimal places.

f(x)=(1/3)^x

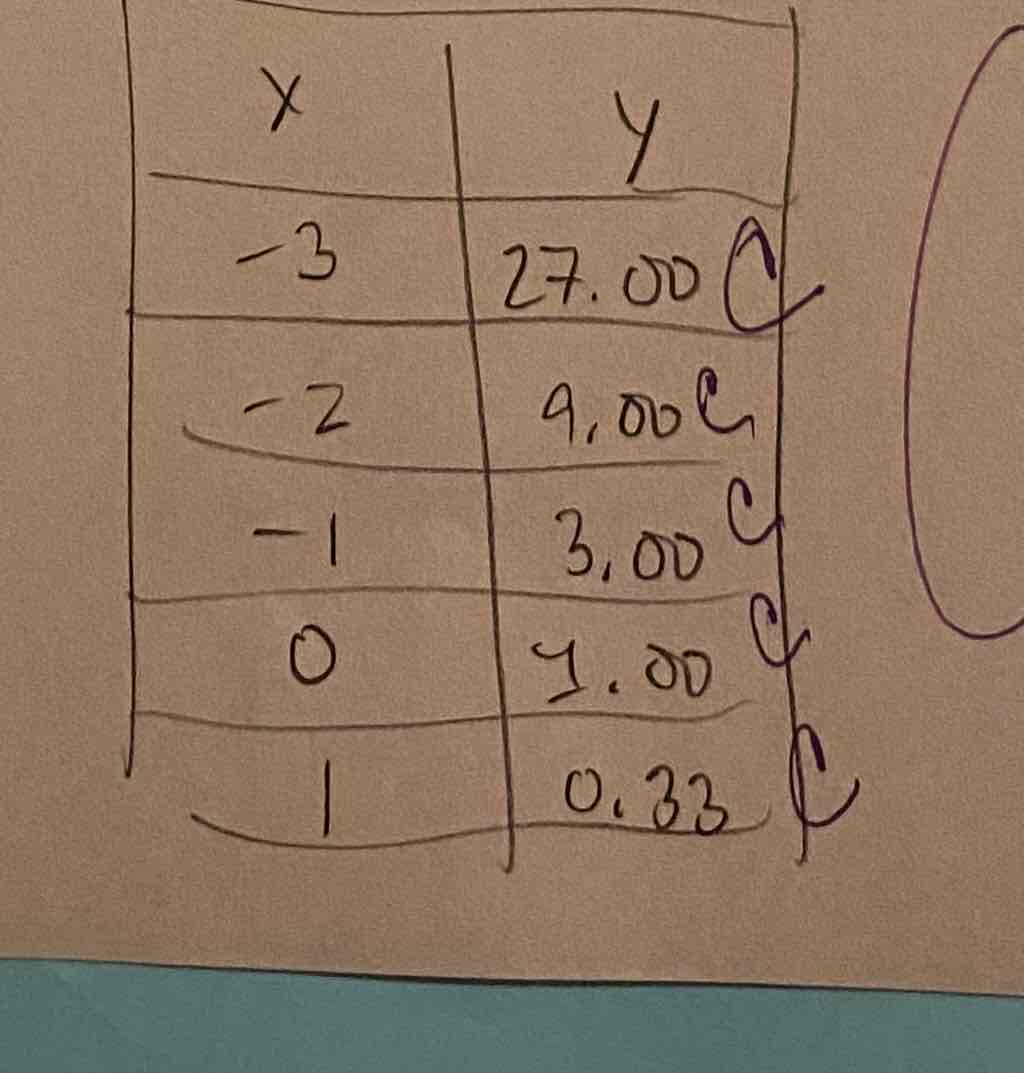
Write the logarithmic equation in exponential form.

Log6(216)=3

d. 6³=216

Write the exponential equation in logarithmic form.

81^(1/2)=9

b. Log81(9)=1/2

Use the properties of logarithms to simplify the expression.

2^(log2(7))

c. 7

Write the exponential equation in logarithmic form.

e^8x=9

d. ln9=8x

Use the One-to-One Property to solve the equation for x.

e^(x²-5)=e^4x

x=5, -1

Evaluate the function at the indicated value of x=81

f(x)=log3(x)

f(81)=4

use the properties of logarithms to expand the expression as a sum, difference, and/or constant multiple of logarithms. (Assume all variables are positive.)

Log(11x³y)

Log(11)+3log(x)+log(y)

Condense the expression to the logarithm of a single quantity.

Ln(x)-[ln(x+2)+ln(x-2)]

Ln(x/(x+2)(x-2))

Use the properties of logarithms to rewrite and simplify the logarithmic expression.

ln(3e^17)

ln(3)+17

​The function k is given by kx=9x. Which of the following expressions also defines kx ?

B. 3^(2x)

Using the power property for exponents and the fact that 9=3², kx can be expressed in this equivalent form.

To solve the equation log8x-3+log8x+4=1, one method is to apply the properties of logarithms to write a new equation that can be used to identify possible solutions. Of the following, which is such an equation?

D. ​x²+x-12=8

Using the product property for logarithms, the given equation has the same solutions as log8x-3x+4=1. Using the definition of a logarithm, this helpful quadratic equation emerges: 81=x-3x+4=x2+x-12.

An equation involves the expression log9(27^x), which is equivalent to a rational multiple of x. By rewriting the expression in an equivalent form, the value of the rational number can be determined without use of a calculator or complicated calculations. Which of the following is an equivalent expression that satisfies this requirement?

D. (xlog3(27))/(log3(9))

Recognizing that both 27 and 9 are powers of 3 allows the change of base and power properties for logarithms to be used. log927x=xlog327log39, which is equivalent to 32x. The rational number is 32.

Let x and y be positive constants. Which of the following is equivalent to 2lnx-3lny ?

A. ln(x²/y³)

The power and product properties for logarithms have both been appropriately applied to rewrite the logarithmic expression in equivalent form. 2lnx-3lny=lnx2+lny-3=lnx2y-3.

What are all values of x for which lnx3-lnx=4 ?

C. x=e² only

The natural log side of the equation can be rewritten in an equivalent form as lnx3x=lnx2,  resulting in the equation lnx2=4. Writing as an exponential equation gives e4=x2 and solving for x results in x=e2 and x=-e2. However, x=-e2  is not in the domain of the original equation because the value of x=-e2 is negative. 

At time t=0 years, the population of a certain city was 23,144. During each of the next 10 years, the population decreased by 4% per year. Based on this information, which of the following models the population as a function of time t, in years, for 0≤t≤10 ?

C. 23,144(0.96)^t

Based on the context of population decreasing by the same percent per year, this is an exponential decay function model of the form abx. The initial value, a, is 23,144 at time t=0 years. The base of the exponent, b, can be understood as a growth factor of 96% per year, which corresponds to a decrease of 4% per year. Therefore, an appropriate model for the population as a function of time t, 0≤t≤10, is given by 23,144(0.96)^t.

The function h is given by h(x)=5·3^(-x/2). What is the value of h(1)?

D. 5/root 3

This is the result of correctly applying the negative exponent property to get 

The function h is given by h(x)=8·2^x. For which of the following values of x is h(x)=256 ?

B. x=5

Solve the equation 8·2x=256. This can be rewritten as 2x=32 by dividing both sides by 8. Therefore, x=5. An alternate approach is to rewrite hx as hx=23·2x=23+x and 256 as 28. Using properties of exponents, 3+x=8 and therefore x=5.

The exponential function g is given by g(x)=5^x. Which of the following expressions defines g^-1(x)?

A. log5(x)

The inverse of an exponential function of base 5 is the logarithmic function of base 5.

Consider the functions g and h given by g(x)=4^x and h(x)=16^(x+2). In the xy-plane, what is the x-coordinate of the point of intersection of the graphs of g and h ?

A. -4

To find the x-coordinate of the point of intersection of the graphs of the two functions, solve the equation 4x=16x+2. Because 16x+2=42x+2, the equation can be rewritten as 4x=42x+2. Therefore, the exponents are equal and solving x=2x+2 results in x=2x+4, which means x=-4.

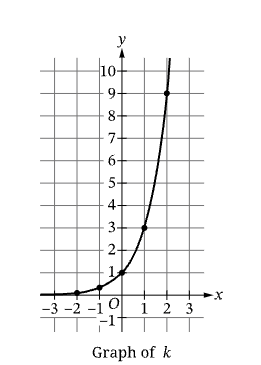
The figure shows the graph of an exponential function k, where kx=bx for b>0 and b≠1. Consider the logarithmic function h (not shown) given by hx=logbx. Of the following pairs of points, which are on the graph of h?

D. (3,1) and (9,2)

Because functions k and h are inverses of each other, if s,t is a point on the graph of k, then t,s is a point on the graph of h. The points 1,3 and 2,9 are on the graph of the exponential function k. Therefore, 3,1 and 9,2 are on the graph of the logarithmic function h.

​The function m is given by m(x)=36^(x/2). Which of the following expressions could also define m(x) ?

A. 6^x

Using the product property, 36x/2=361/2x. The fractional exponent 12 indicates the square root of the value, or 361/2=6.

Which of the following expressions is equivalent to log3(x^5) ?

C. 5log3(x)

Using the power property for logarithms, log3x5 can be rewritten as 5log3x.

​If m=log3(81), which of the following is also true?

B. 3^m=81

This is the result of correctly translating an equation involving a logarithmic expression to one involving an exponential expression.

The function f is given by f(x)=log2(x). What input value in the domain of f yields an output value of 4 ?

B. 16

The function f yields an output value of 4 when log2(x)=4. This is equivalent to 2^4=x, and the input value is x=16.