C21 - Kinetic Theory of Gases

Kinetic theory of gases

Describes microscopic movements of gas molecules in a container

• cubic container, side length d

• identical molecules, large N

• V_gas « V_container

• Elastic collisions only, no IMFs

  • Elastic collisions occur with walls & other molecules

• isotropic motion (any speed, any direction)

pressure-KE_micro theorem

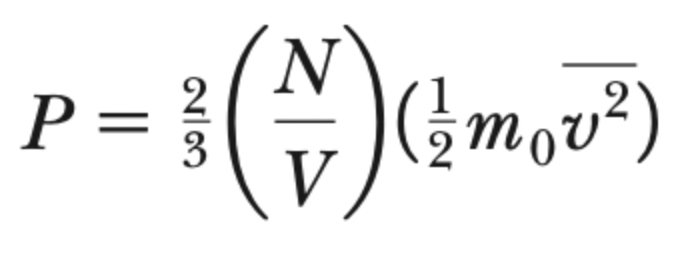
temperature-KE_micro theorem

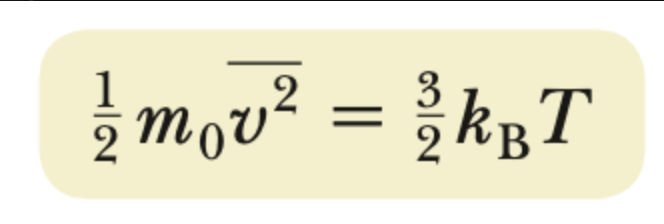
K_{total translational}

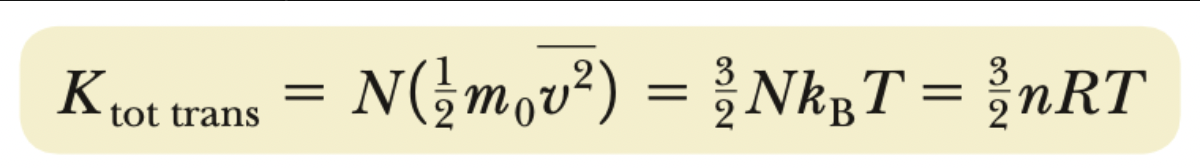
v_rms

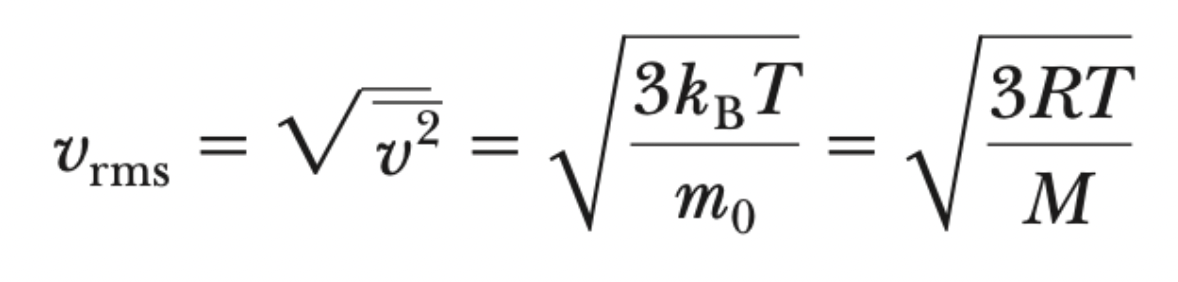
v_mp

v_mp = sqrt(2RT/M)

v_avg

v_avg = sqrt(8RT/πM)

theorem of equipartition of energy

each degree of freedom contributes an equal amount of energy to the system, E = k_bT/2

degrees of freedom

individual means of storing energy

• translation, x, y, z (3)

• rotation, x-axis, y-axis (2)

  • I_z-axis negligible for linear molecules

• vibration: U_elastic, KE (2)

Molar specific heat

amount of energy required to increase 1 mol of a substance by 1K (based on process)

• Q_{isovolumetric} = nC_v∆T

• Q_isobaric = nC_P∆T

  • C_P > C_v

C_V (general eqn)

C_V = (1/n)(dE_int/dT)

C_P (general eqn)

C_P = R + C_V

γ (general eqn)

γ = C_P/C_V

molar specific heat constants

translation:

• C_V = 3R/2 = 12.5 J/(mol • K)

rotation:

• C_V = 5R/2 = 20.8 J/(mol • K)

vibration:

• C_V = 7R/2 = 29.1 J/(mol • K)

adiabatic processes

• PV^γ = constant

• TV^γ-1 = constant

distribution of molecular speeds

• v_rms > v_avg > v_mp

  • v_rms: assume all particles have v_rms, calculate accurate values for pressure or energy

  • v_mp: speed that most particles have at any given point in time

  • v_avg: averaged speed

k_b (again)

1.38 × 10^-23 J/K