Fourier Transforms and Spectroscopy

Signal to Noise ratio

• General goal getting the ratio as large as possible

• Or achieve equal S/N in less time

Fellget Advantage

Two Experiments to Lower S/N

Can get signal by getting peak height or area, and get the noise by getting flat section of baseline and take the standard deviation and get the noise.

The sum of the two peaks creates a peak that is twice as big due to constructive interference and the noise < double the noise whereas the signal is doubled, running the experiment twice causes the time to take twice as long.

Achieve the same improvement in S/N without increasing time

Need to increase the amount of data we collect in a fixed-time interval: achieve a greater flow rate of useful data. → multiplex

Fellget/Multiplex Advantage

 This improves the S/N by a factor of sqrtN → is number of repetitions (objects being weighed at once)

Fellgets advantage is only realized for noise sources that are detector limited rather than source limited

Detector Limited

 function of the equipment being used, and independent of the sample and it’s size

Source Limited

function of the sample and it’s size

Multiplex Weighing

• Means weighing multiple objects at once, which means that the mass on the pan is higher.

• If the uncertainty of the weighing procedure gets larger with the mass increase, you nullify your Fellgett’s advantage

• Not really an issue with the balance

Infrared Spectrophotometry

Light→ monochromator→ sample → detector→ data system

Fourier Transform Infrared Spectrophotometry

Beam is made out of KBr

• Impact of this: Thrown out 50% of our incoming beam intensity

• Starting position is the Beam Stop, translates to the ZPD, then reverses and moves back to the Beam Stop

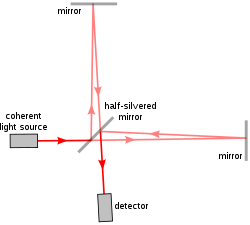
Old Way

-scan the monochromator from 4000 cm^-1 to 600 cm^-1, collecting an analog stream of %T data as the instrument scanned cm^-1

Took 2-3 mins

Revising the Old Method

• Involved in a single data point at a time in series

• Need to multiplex (increase flow of information) to achieve Fellgets advantage

• How? Remove monochromator and work with all the wavelengths of light at once

• major multiplexing, so no linearly independent equations

• Have a spectrum that consists of one data point

Zero Path Difference

At this point, the moving mirror is equidistant from the beam splitter compared to the fixed mirror

• At ZPD, 2 beams are split by the beam splitter, travel equal distances to the mirrors and back, and are recombined to go to the detector

• Since the paths are exactly the same, the light waves are exactly in phase

• The position of ZPD +/- ¼ wavelength varies with every different wavelengthFrequency Do

Interferogram

Output of the summed light beams as the mirror moves

Frequency Domian

signal gathered when plotting cm^-1 on the X axis in IR

Interferogram

 Is not an IR spectrum, but it contains all the information to produce one

Since the translating mirror moves at a constant rate, the X axis is equivalent to time (time domain signal)

Fourier transform Algorithm

• Best results, sum together the multiple scans as interferograms, then take the FT of the sum at the end, to get good data for the multi-scan, the interferometer must be able to reproduce exactly the movement of the translating mirror - speed and pathlength

To ensure reproducibility, a He-Ne laser is bounced off the moving mirror to allow precise monitoring of its movement

FT application (chemometric methods)

Smoothing of noisy data - common for chromatography

“Boxcar” averaging: averages multiple points in a certain data set (11 points) eliminated high frequency noise

Smoothing with FT

• Takes advantage of the fact that most analytical signals are low-frequency effects

• Bulk of noise is high frequency variety

Transition Point

(vertical line from a multiplier 1 to 0) is referred to as the frequency cutoff

Low frequency bandpath

 lets low frequencies pass, meaning the high frequencies are filtered out

How to do smoothing

Take the noisy data set, apply FT algorithm

Converts time domain to the frequency domain, draws resultant trace

Take the post FT trace, and apply a low frequency bandpass filter

Normally this is an optical piece or an electronic circuit, but in this case with the algorithm a digital filter

The FT data is multiplied by the digital filter and then inverse FT algorithm is applied, converts back to the time domain