Biostatistics exam 3 - Adjusting for multiple comparisons

Family-wise error rate (FWER) equation

α = alpha

n = number of comparisons (# of tests)

• gives you the probability of committing a type I error

• Examples:

- chocolate study: 60% probability of Type I error

- astrological study: 70% probability of Type I error

• the more tests you run, the higher the probability of a Type I error

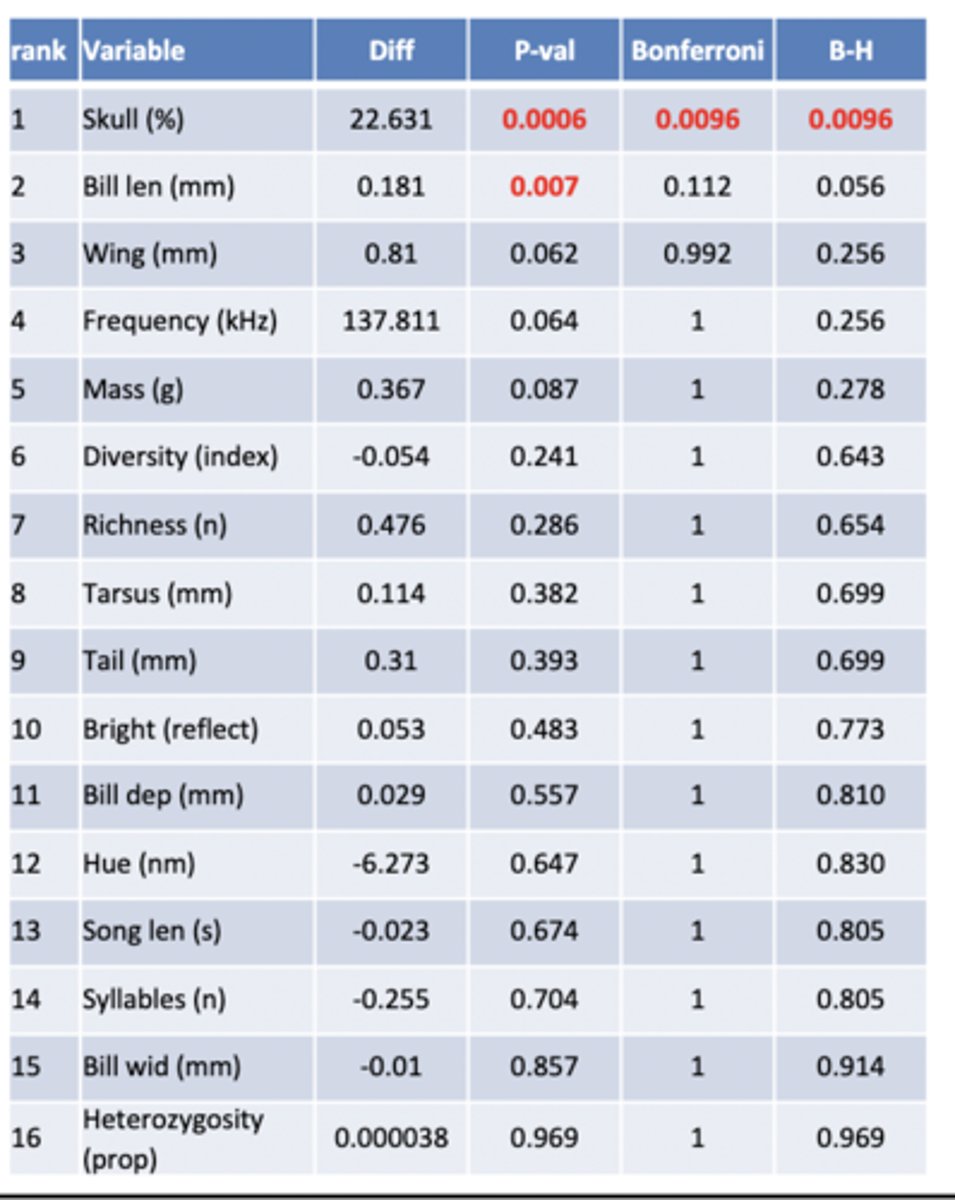
Bonferoni adjustment

• used to help adjust P-values due to multiple tests

• you run the adjustment on each other of the tests

Padj = P * k

• k = number of tests

• P = orignal p-valus

• Note: Maximun Pajd is 1

• some people say it is too harsh

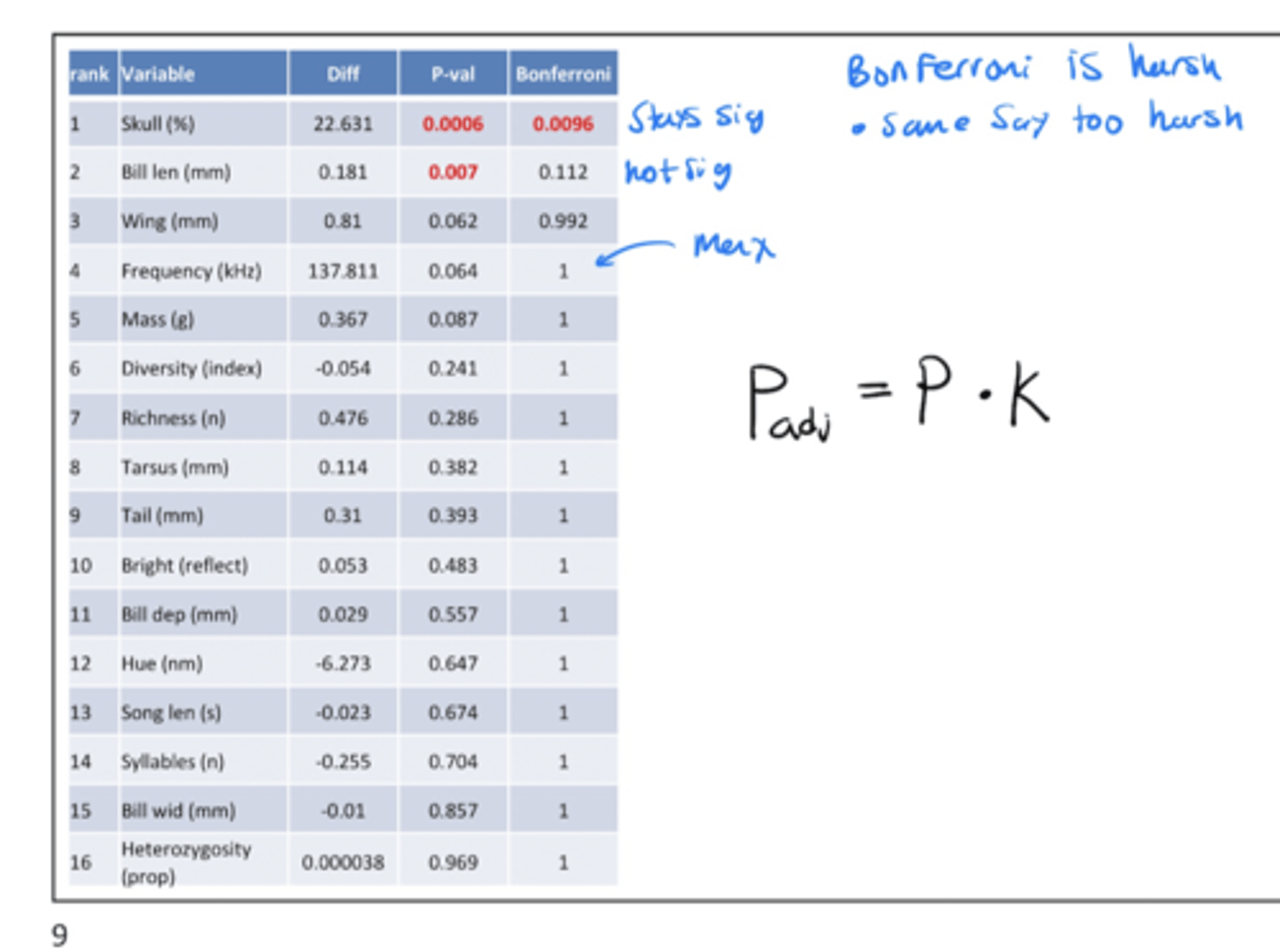
Benjamini-Hochberg adjustment

• Much more permissive and popular method

- Alias "False discovery rate"

• Sorts P-values low to high

• NOTE: the value cannot exceed BH of rank i+1

- Any adjusted P-val can't be higher than the one next to it

• k = number of tests

• i = rank of that particular test

- lowest p-val i = 1

* The highest rank will have the the same p-val from OG test bc k/i = 16/16 (in this test example)

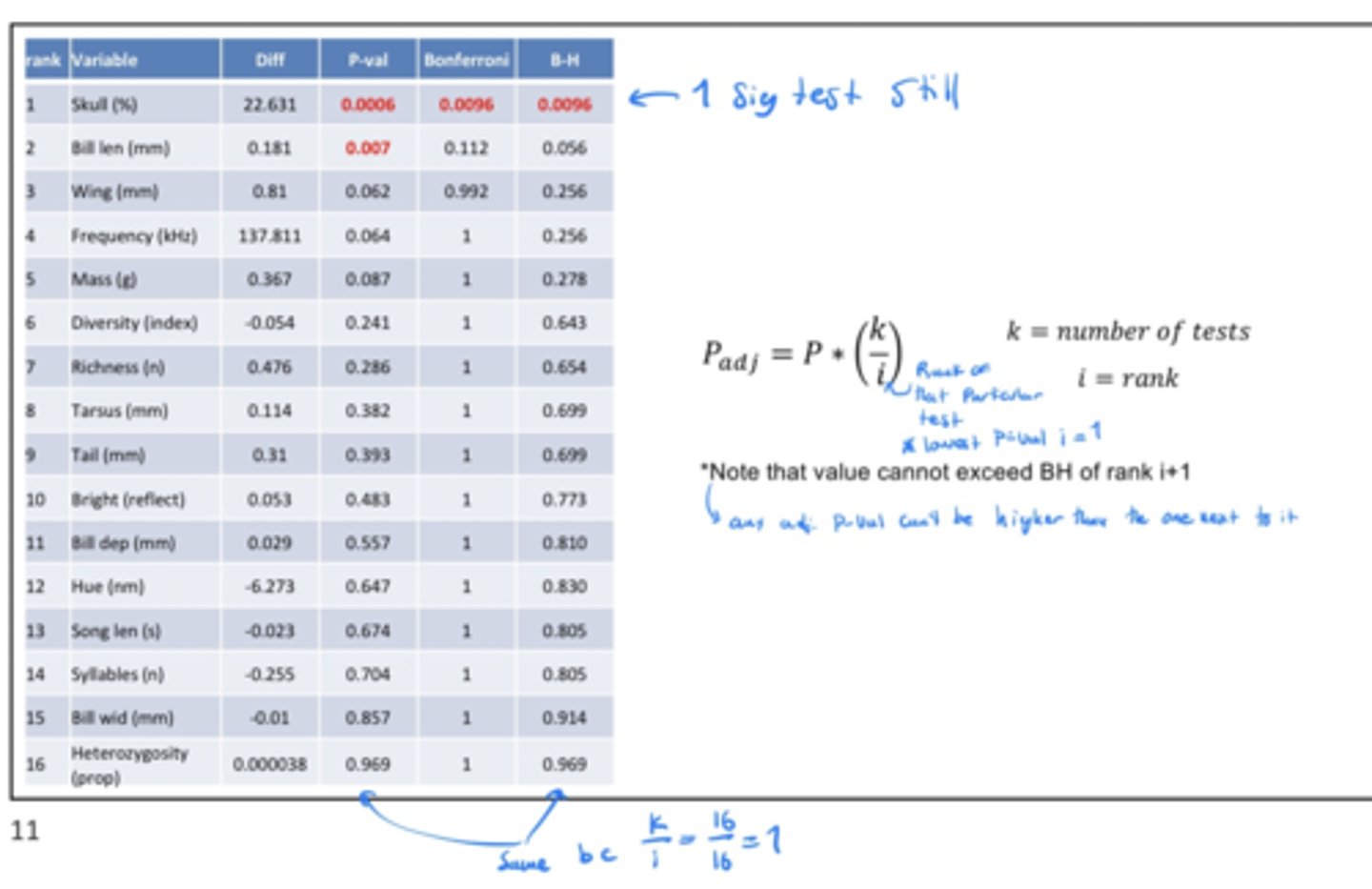
Importance of adjusting P-values

• changes biological interpretation

In this example:

• No correction

- 2 significant variables

- 3 additional variables have a P-val between 0.05 and 0.1 ("marginally significant") (so an inc. in sample size might make it significant)

• With correction

- 1 significant variable

- 1 marginally significant variable