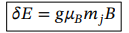Quantum mechanics term 1

Compton scattering equation

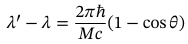
Equation for energy levels in an atom

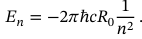
Postulates of Bohr’s model of the atom

-electrons move in fixed circular paths around the nucleus

-electrons in orbit do not radiate

Equation for electron angular momentum in Bohr’s model

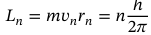
Equation for electron orbital radius in Bohr model

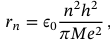
Heisenberg’s uncertainty principle

Schrodinger Equation

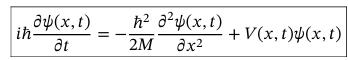
Probability of finding a particle in strip x —> x + dx

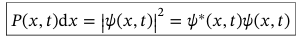
Normalisation condition for 1D system

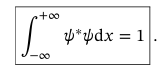
Time Independent Schr. Eq (TISE)

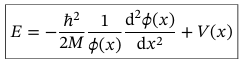
Solution to TISE

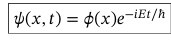
What effect does time dependence have on the probability of finding a particle in x—> x+dx and when is it significant?

-change of phase of wavefunction

-relevant when there are two contributions with different phases

Energy for each wavefunction describing a particle in an infinite potential well

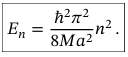
Conditions for a valid wavefunction

-function must be continuous and single valued for all positions and times

-integral of modulus squared of the function must be finite as to be normalised

-first derivative of wave function must be continuous everywhere except where potential has infinite step

Potential of mass-spring system

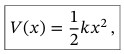
Energy for state n of the harmonic oscillator

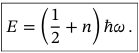
Zero Point energy

The lowest possible energy that a quantum mechanical system may have, which is not zero. In the case of a harmonic oscillator, it corresponds to the energy of the ground state.

Hermite Polynomials

A set of orthogonal polynomials that arise in the solution of the quantum harmonic oscillator, associated with the energy eigenstates.

Postulate 1 of quantum mechanics

For every dynamical system there is a wavefunction that is a continuous, square-integrable and single valued function of space and time.

Hamiltonian operator

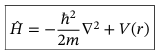
Momentum operator

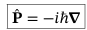
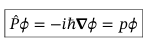
Eigenfunctions of the momentum operator

Plane waves with eigenvalues p = ℏk

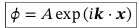
Hermitian operators

Operators that satisfy this equation

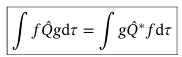
Postulate 2 of QM

Every dynamical variable is represented by a Hermitian Operator who’s eigenvalues represent possible results of measurements of a given variable

Postulate 3 of QM

Position and momentum operators are r and −𝑖ℏ∇. All other operators are the same as in classical physics

Orthonormality relation

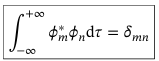
General wavefunction of the system

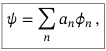
Coefficients in equation for general wavefunction of a system

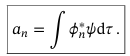
Eigenvalue equation for continuous variables

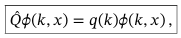
Orthonormality of eigenfunctions for continuous variables

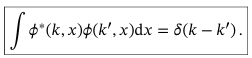
General wavefunction for continuous variables

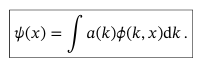
Coefficients a(k) in the equation for general wavefunction of continuous variables

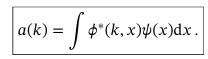
Expectation value

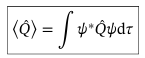
Commutator between x component of momentum operator and the position operator

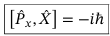
Commutators between i and j components of position operator and i and j components of momentum operator

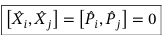
Commutator between i component of momentum operator and j component of position operator

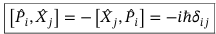
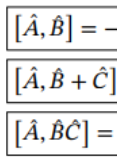
Commutator identities

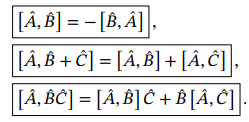
Generalised Heisenberg Uncertainty principle

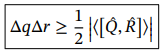
5th Postulate of QM

Between measurements, the development of the wavefunction with time is governed by the TISE

Time dependent wavefunction

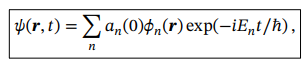
Degeneracy

two or more states with distinct wavefunctions which have the same eigenvalue of a dynamical variable

Ladder operators definition

operators that move us up and down the ladder of states where each step is a particular energy eigenstate

Angular momentum operator

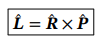
Operator for the square of the magnitude of angular momenum

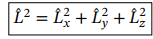
Angular momentum ladder operators

Schrodinger equation in 3D

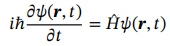
Hamiltonian operator in 3D

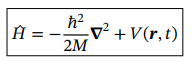
Potential energy operator in 3D

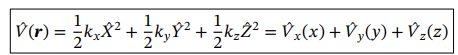
Potential function from a nucleus

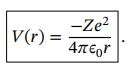
Condition between n (quantum number) and l (orbital angular momentum) for a hydrogen like atom

l < n

Energy levels in hydrogen like atoms in terms of energy of the ground state

E_{n}=-\frac{13.6Z^2}{n^2}eV

Change in energy of state when an energy level with fixed n and l splits due to the value of magnetic quantum number, m

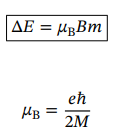
Adding two angular momenta possibilities

• each result has a distinct probability

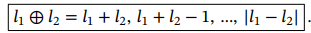
Pauli Matrices for fermions

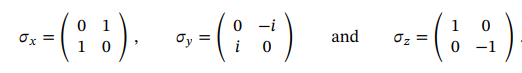
Spin ½ operators in terms of Pauli matrices

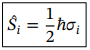
total angular momentum

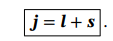
Spin orbit coupling operator

f\left(r\right)=\frac{\mu_0Ze^2}{4\pi M^2r^3}

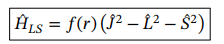
Hamiltonian operator of the effect of an external magnetic field

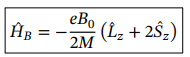
Correction to energy states, including both external magnetic field and spin-orbit coupling

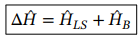
Correction to energy for strong field zeeman effect

m_l and m_s eigenvalues of operators L_z and S_z

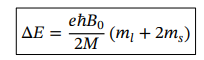
Correction to energy for weak field Zeeman effect