AP Calc BC Integrals Pt 2

Remember +C

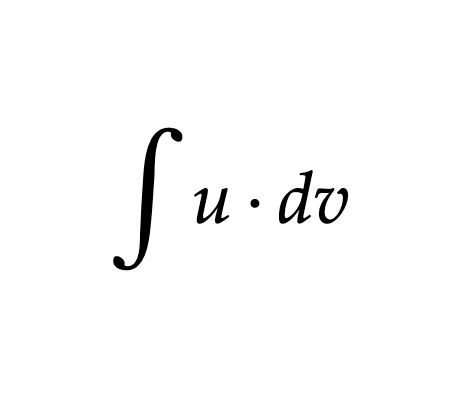
Integration by Parts

Use integration by parts, or tabular method.

• Use tabular method if the derivative of u eventually goes to 0

• Otherwise, do uv - integral(v du)

  • Let u = x² or any other x to the n UNLESS ln(x) is present; then let u = ln(x)

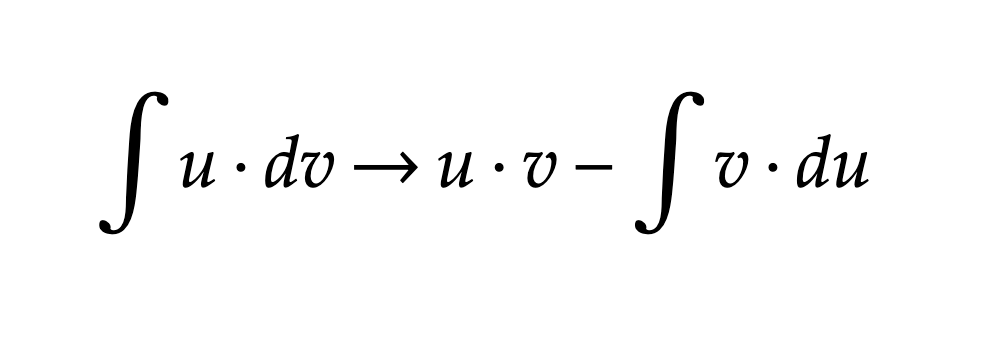
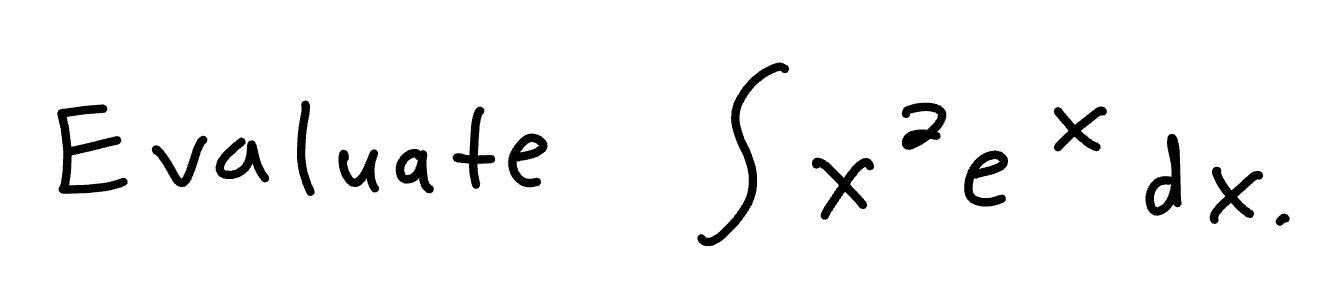
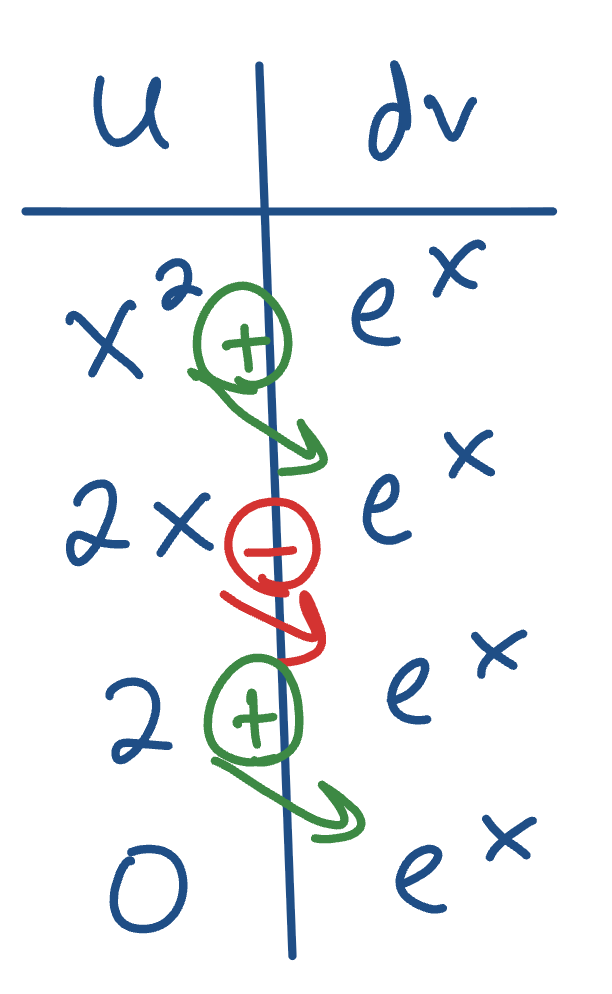
Tabular Method Example

Take derivative of u until it reaches 0, integrate dv until you reach the 0 on the left side; then alternate + or - diagonally going down

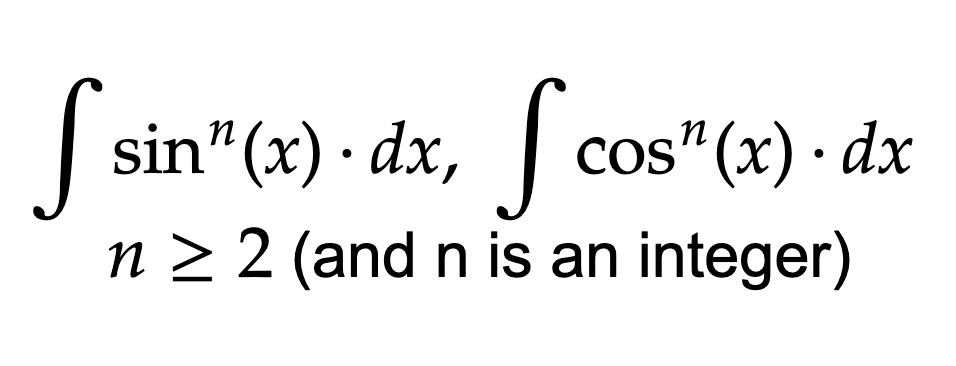
Form 1 of Trig Integrals

If n is odd, save a factor, use a pythagorean identity to convert everything to the other trig function, u substitute so the factor you saved becomes du, then solve.

If n is even, write it as a power of a trig squared. Then use a power reducing identity on the trig squared and FOIL out what you get. Then, distribute the integral and solve (you may have to do multiple power reducing steps).

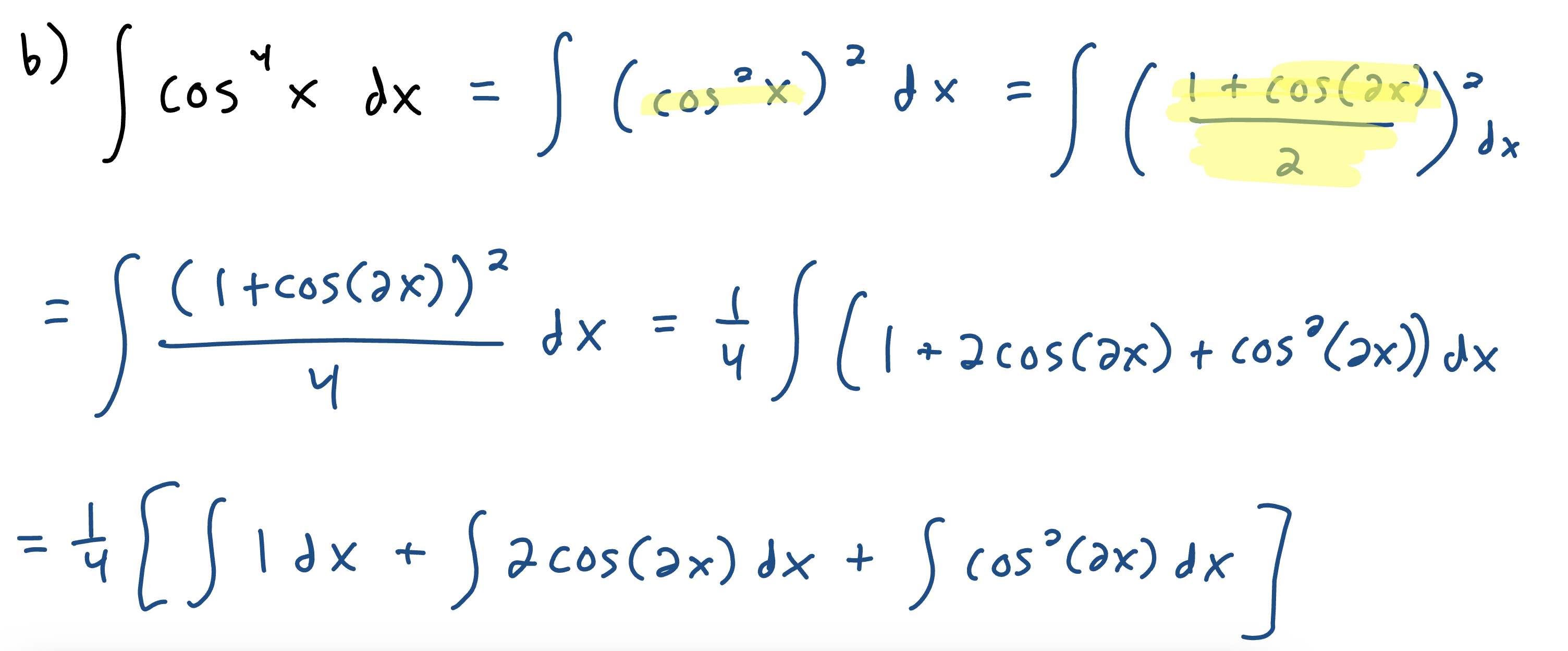
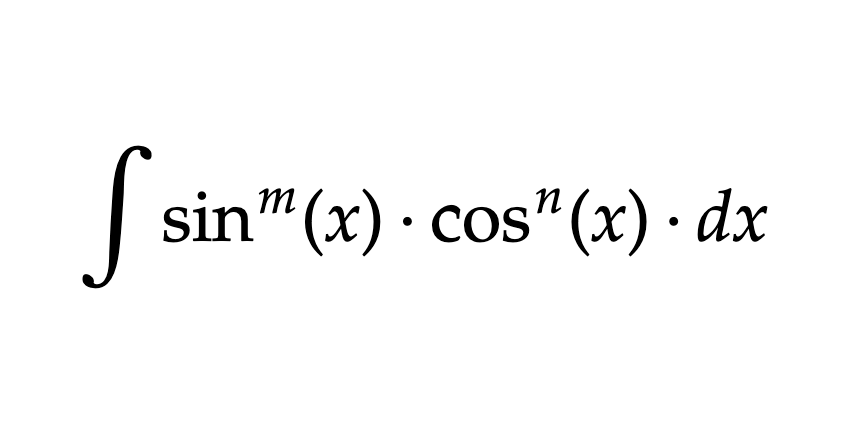
Form 2 of Trig Integrals

If at least one power is odd, save a factor of any odd power. Use a power reducing formula and convert everything left into the other trig function. Then, u sub for the other trig function, so the factor you saved becomes du.

If both powers are even, use power reducing to get everything into the same trig function. Then, use Form 1 to solve the integrals you get.

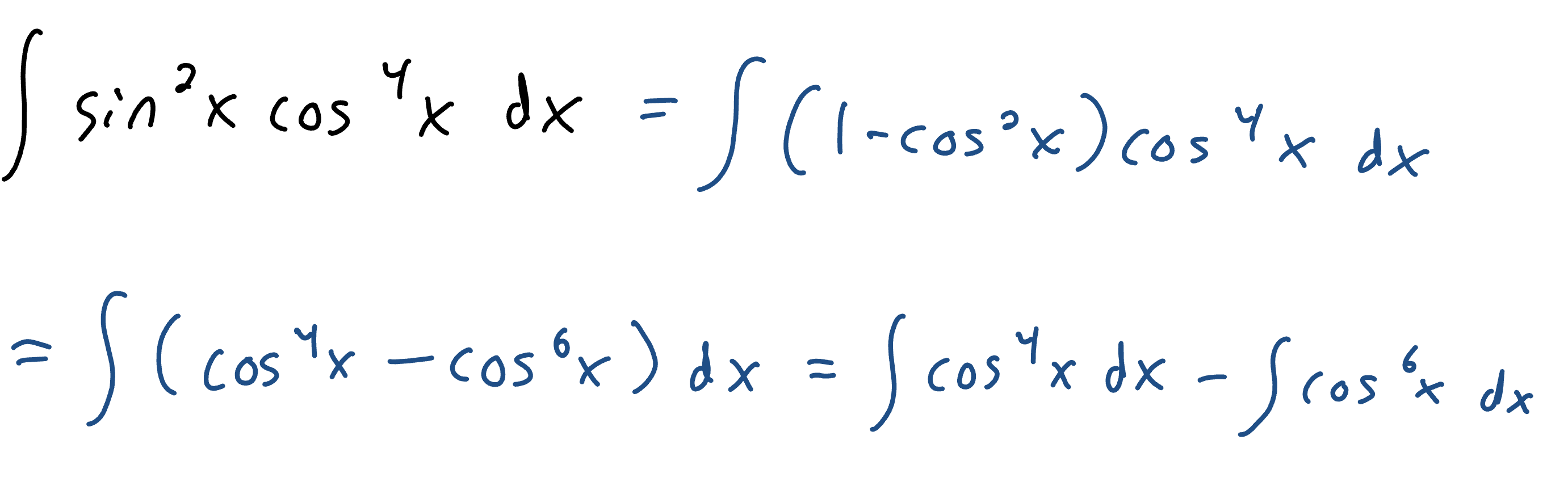
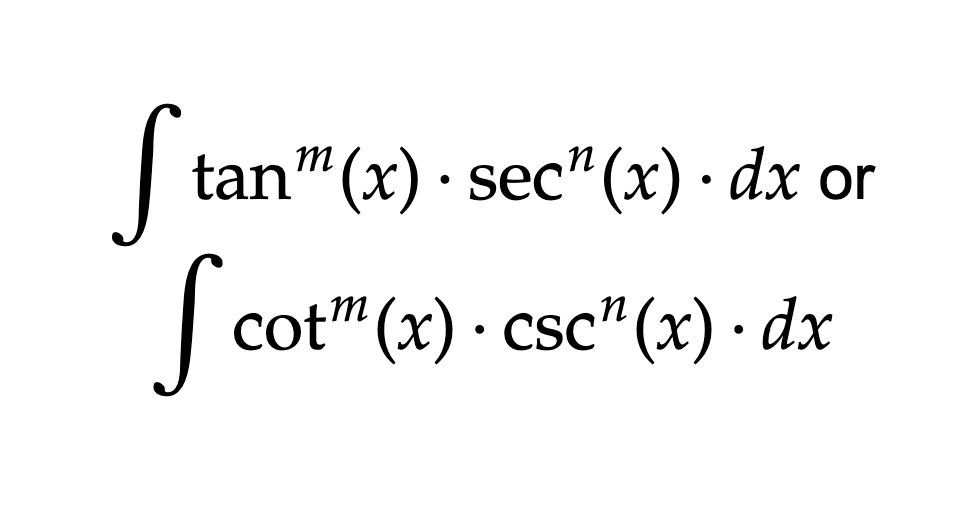
Form 3 of Trig Integrals

If n is even, save a sec²x or csc²x and convert the other sec’s or csc’s into tan/cot. U sub and your du should be what you saved.

If both n and m are odd, save a sec(x)tan(x) or csc(x)cot(x). Convert the tangents/cotangents into secants/cosecants using pythagorean identity; u sub, and your du should be the saved bit (watch out for negatives on the csc/cot integral).

If n is odd but m is even (or 0), you need to use Integration by Parts; let I (or any letter) equal the integral, and you’ll see the I pop up later while integrating. Then just replace the integral with I, and solve for I by getting it on one side.

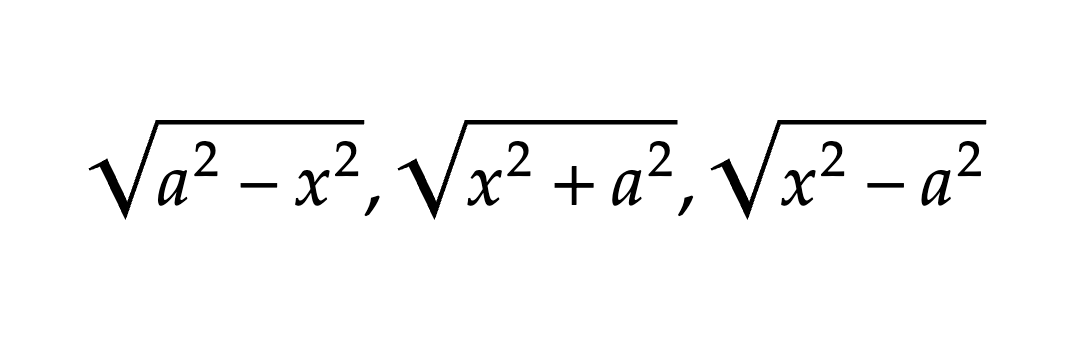
Trig Substitution

Follow the substitution in the image; replace x in the entire integral with your plug in, not just under the root, and make sure to find dx and plug that in as well.

• if it’s a definite integral, plug the limits into x = a * … so you get (limits) = …; then solve for theta and replace your limits

Once you plug in everything, you should be able to simplify what’s under the root into something that you can use a Pythagorean identity on. Then, cancel out everything and solve. Once you get your final answer, draw a triangle and plug in your original substitution; convert your result based off this triangle.

• Only convert your result if you are NOT doing definite integral. Since you convert the limits while doing a definite integral, you can just plug into theta after you find the antiderivative.

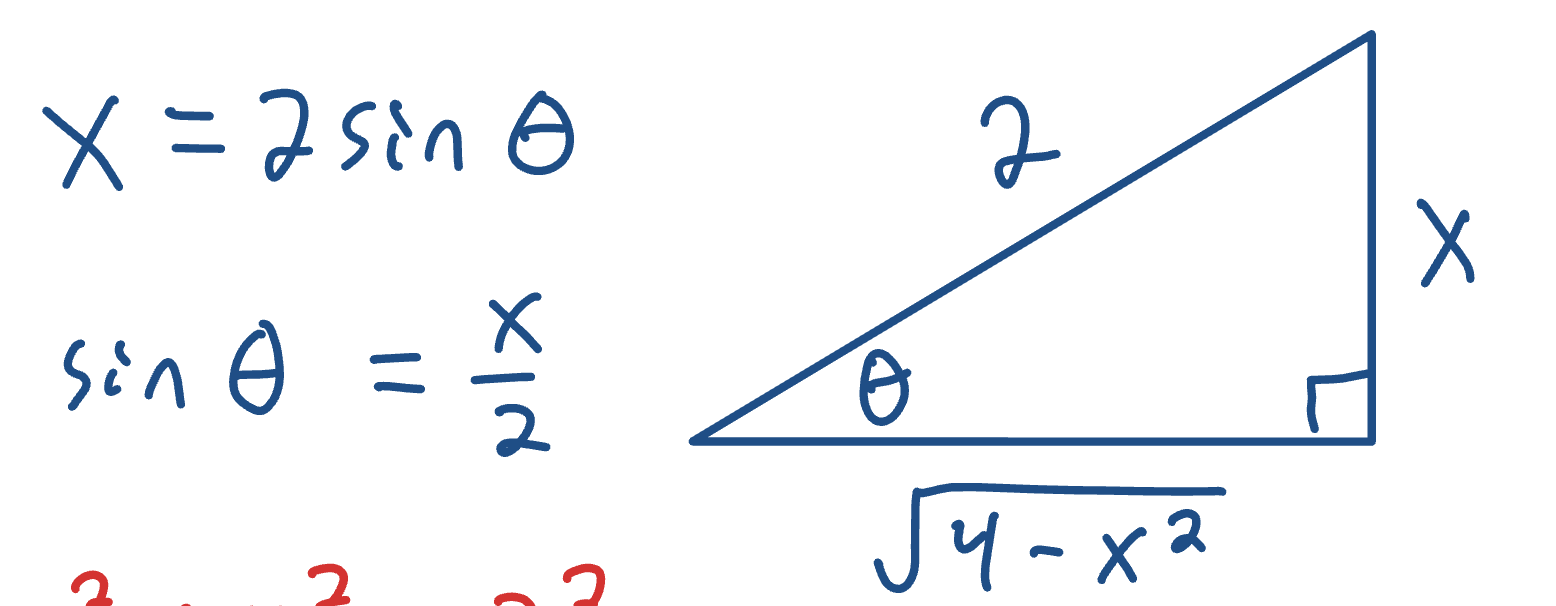
Trig Sub: Triangle

For this example, the substitution created a triangle as shown. If (for example) you ended up with cos(theta) in your answer, it would become √(4-x²) over 2.

If you end up with theta by itself in your answer, solve for theta from the original substitution; in this case, theta would be inverse sin of (x/2)

• Again, only convert theta back to a function of x if it is an indefinite integral

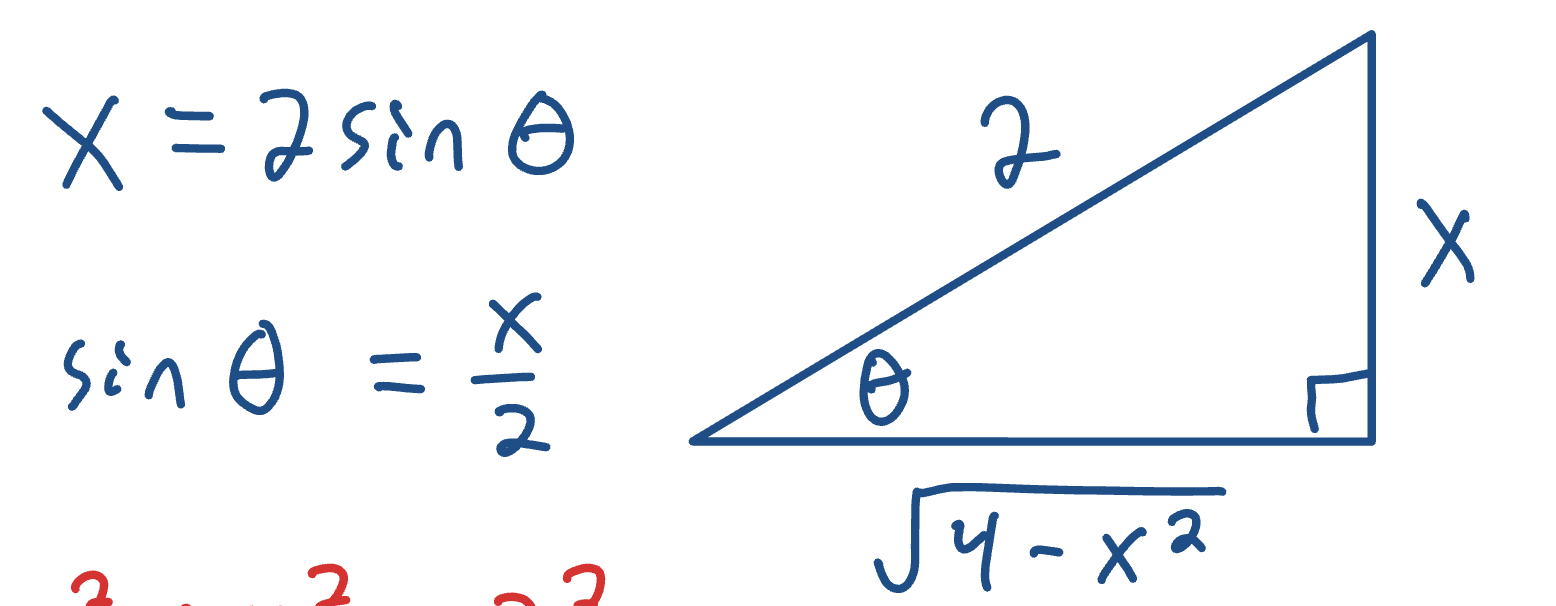
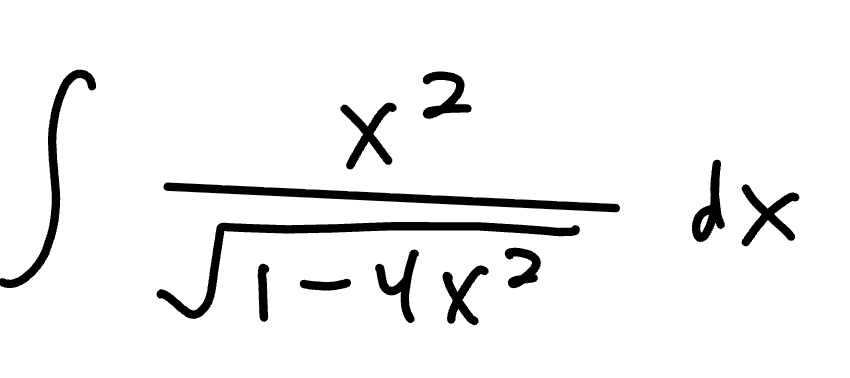
Trig Sub: 2 step with U sub

If the x under the square root has a coefficient, you need to U sub for it in order to use a trig sub. After you u sub and get a root with u with no coefficient, then trig sub as normal. At the end, convert theta back into u, and then plug your u sub into the u’s in your answer.

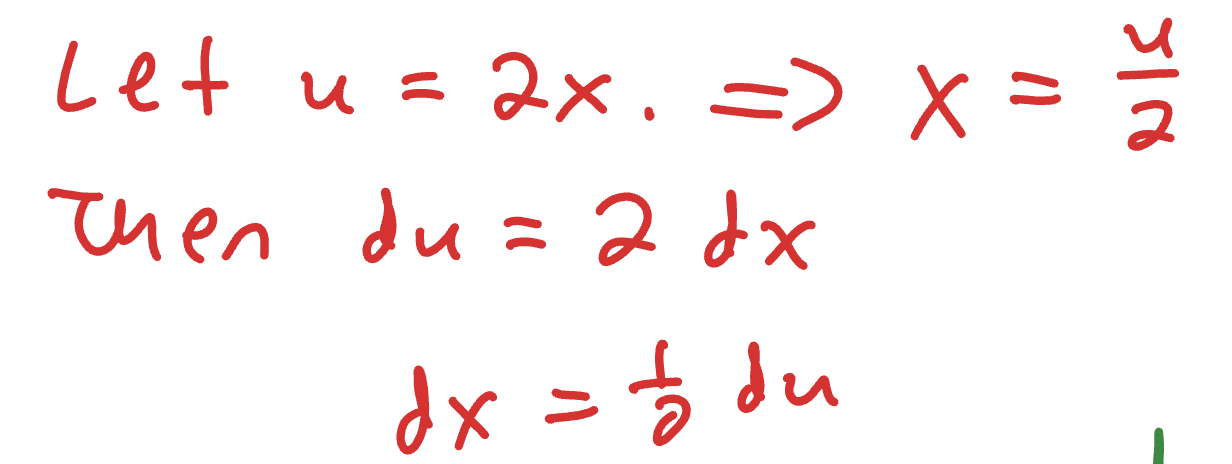
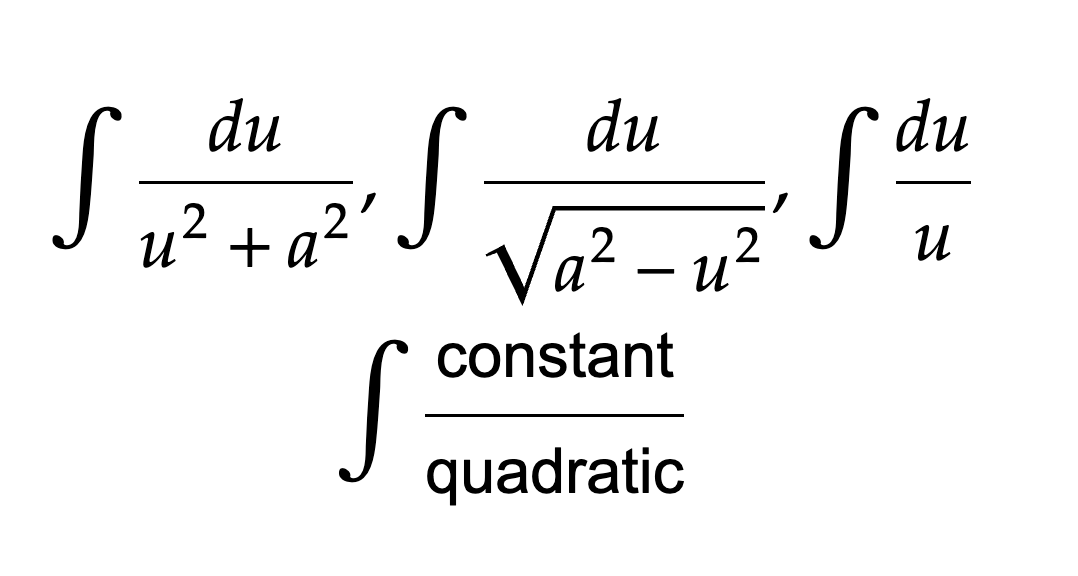
Rational Integrals: Shortcuts

In the image are some shortcuts to save time on a trig sub. You can do the inverse trig shortcuts by hand, but it’s much faster just to know the formula, especially since these show up a lot when integrating rational functions.

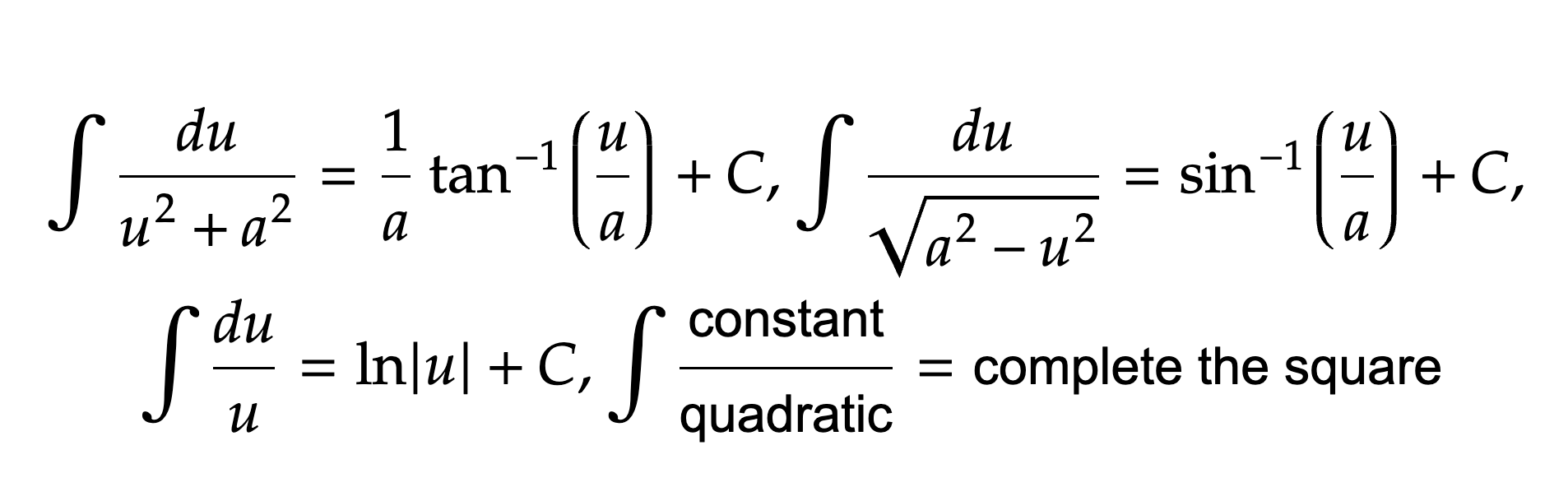
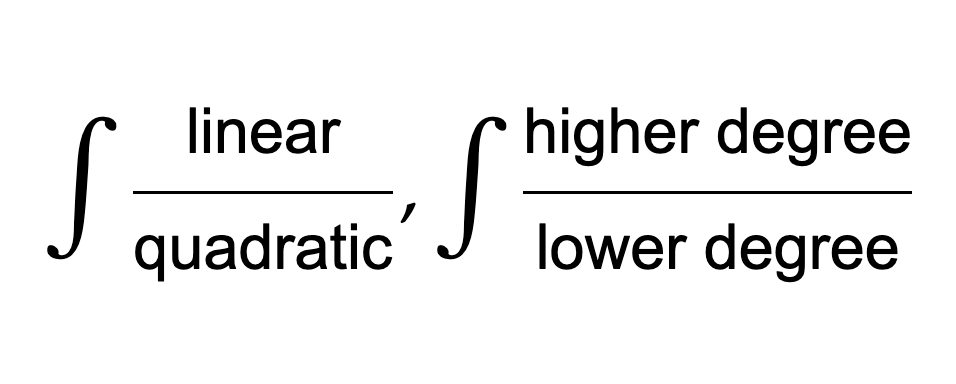
Rational Integrals: Complicated Fractions

If you end up with a linear over a quadratic, split it into two fractions:

• One fraction should be u prime over u (you may need to multiply out some constants to get this to work) so you can use the ln formula

• The other fraction should be a constant over quadratic, so you can complete the square and use an inverse trig shortcut

If the degree on top is larger than the degree on bottom, long divide (or synthetic division if the divisor is a linear term with no coefficient, but long division always works). You will end up with a regular function of x that should be a simple integral plus a fraction that you should be able to solve using the other methods here (the degree on top won’t be bigger anymore).

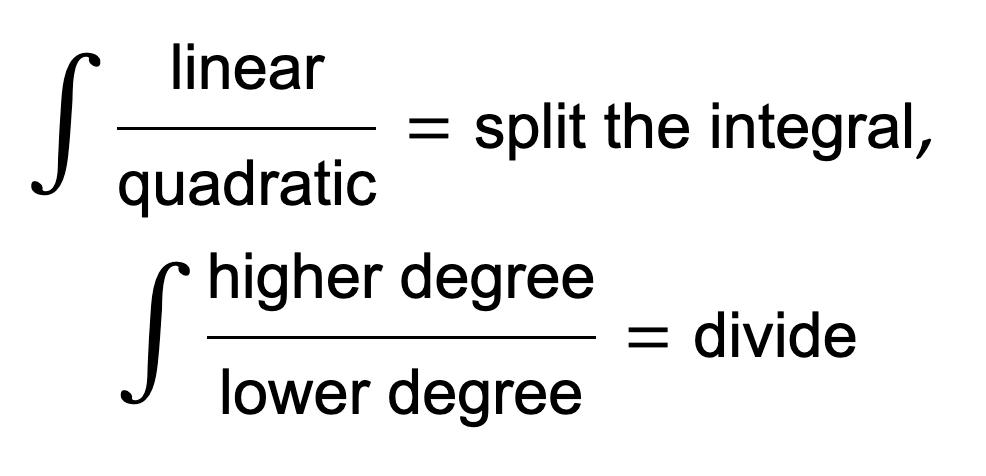
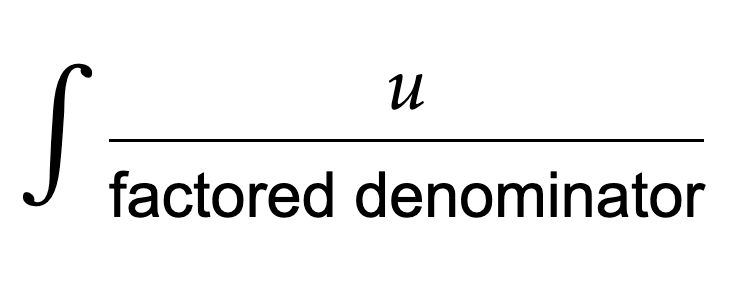
Rational Integrals: Factored Bottom

If the bottom of the integral is factored, use partial fraction decomposition. This will split up the integral into multiple fractions, each of which should be solvable using other methods like u sub, ln shortcut, or linear over quadratic strategy.

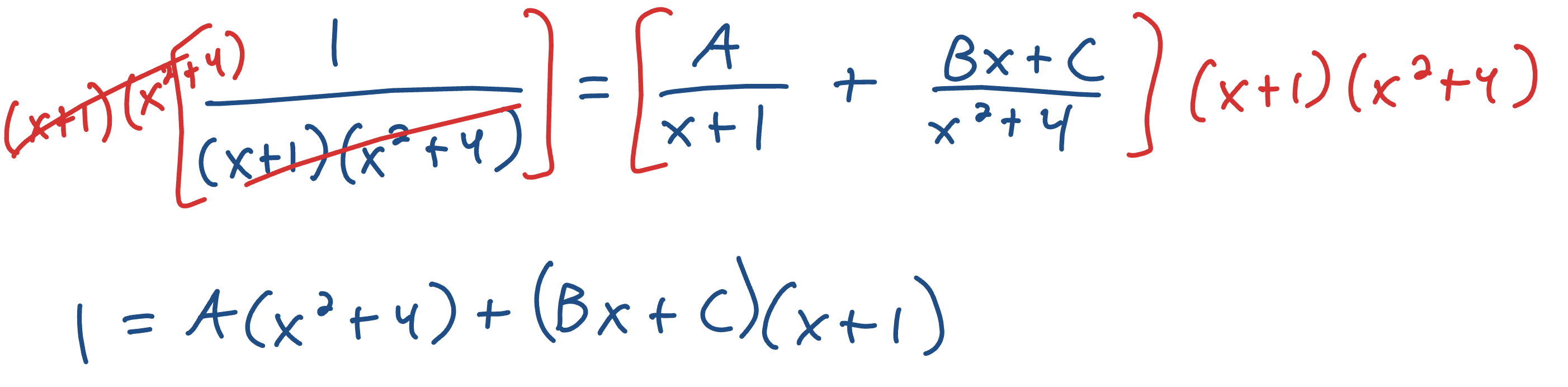
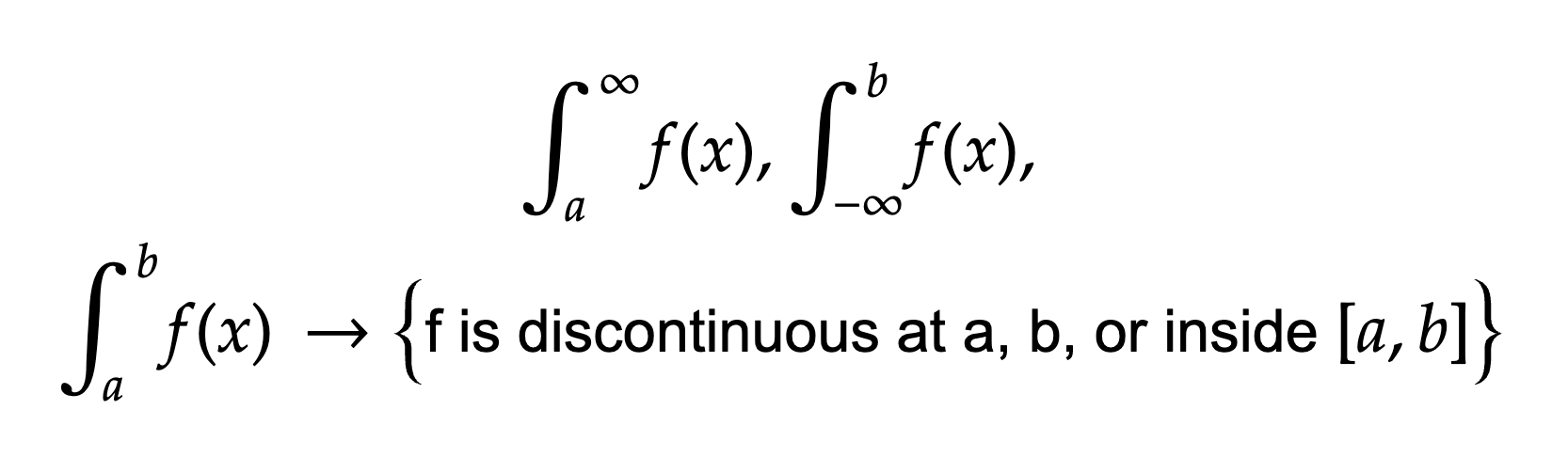
Improper Integrals

If any of the conditions are satisfied:

• If a or b are infinity (or negative infinity), do a limit as a/b approaches infinity/negative infinity. After you find the integral, try and see the end behavior or what happens as a/b approaches infinity. If it approaches a value, add that to the other bit of the definite integral and write it converges to that. If it does not approach a value (like sin(x)), write diverges

• If the integral is discontinuous at the limits, write a limit where a/b approaches the limit from the right or left of the integral. Then look at what happens to the integral as you get really close to the limit. If it converges on a value, write that (plus the other bits of the definite integral). If it doesn’t, write diverges

• If the integral is discontinuous between the limits, split it into two integrals and write two limit integrals (for example 0 to 2 discontinuous at 1 would become 0 to 1 and 1 to 2) and see what happens from the left and right of the discontinuous point

If a limit “converges” to infinity, do not write that it equals infinity. Do not plug infinity into a limit statement either. If a limit approaches infinity, write diverges, since infinity is not a number.

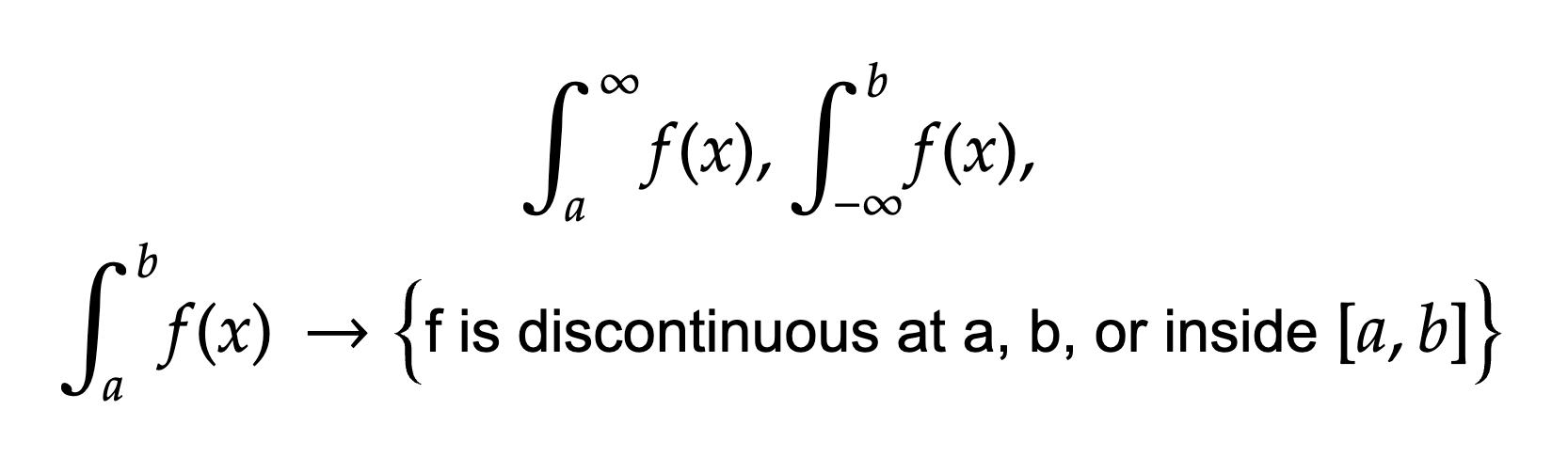
Other Useful Formulas (not already shown)

• Integral of tan(x) dx is ln|sec(x)| + C

• Integral of sec(x) dx is ln|sec(x) + tan(x)| + C

• sin²x + cos²x = 1

• 1 + tan²x = sec²x

• 1 + cot²x = csc²x

• cos²x = (1 + cos(2x)) over 2

• sin²x = (1 - cos(2x)) over 2

• sin(2x) = 2sin(x)cos(x)

• cos(2x) = cos²x - sin²x (Probably don’t need this one)