Course 8 - Models of product differentiation

Introduction - Products

Most products ≠ perfectly substitutable → Reasons:

1. Physical characteristics of products ≠ idem

2. Products = branded differently / designed for specific consumer groups

Economists distinguish vertical & horizontal product differentiation

HORIZONTALLY product differentiation - Definition

• When each product = preferred by at least 1 consumer group

OR

• When for same P consumers disagree on product they prefer

Ex.: Marketeers in fast moving consumer goods design product offers for groups of consumers according to their age, social-economic groups, passions, …

Introduction - Products

Most products ≠ perfectly substitutable → Reasons:

1. Physical characteristics of products ≠ idem

2. Products = branded differently / designed for specific consumer groups

Economists distinguish vertical & horizontal product differentiation

HORIZONTALLY product differentiation - Definition

• When each product = preferred by at least 1 consumer group

OR

• When for same P consumers disagree on product they prefer

Ex.: Marketeers in fast moving consumer goods design product offers for groups of consumers according to their age, social-economic groups, passions, …

HORIZONTALLY product differentiation - Firm perspective

In horizontally differentiated product markets, fims choose:

• price of the product &

• its position in the product space

Usually assumed that consumers = located on a line (Hotelling) / circle (Salop) & incur cost when purchasing product far from them

→ Geographical interpretation:

Consumers incur higher cost to move a more distant shop

→ Products ≠ perfectly substitutable, consumers incur psychological transportation cost when consuming product that ≠ ideal

Proof:

1) Show that in Bertrand model where firms = located in different positions on the line, both firms set P above MC & enjoy positive profits

2) If firms choose locations, but not choose P, they choose to be located in same place

3) Firms choose P & location with linear & quadratic transportation costs

Proof - (1) P choice in differentiated product market (Bertrand model)

Bertrand model where 2 firms produce differentiated products:

• 2 producers denoted 1 & 2 with MC c = located at extreme locations of the [0,1] interval on which consumers = uniformly distributed

• Firms max π_i = (p_i - c)Q_i(p_i,p_j)

• Indirect U fct of consumer located in x with preferred product U r & consuming 1 unit of product i located in l_i = r - T |l_i - x| - p_i

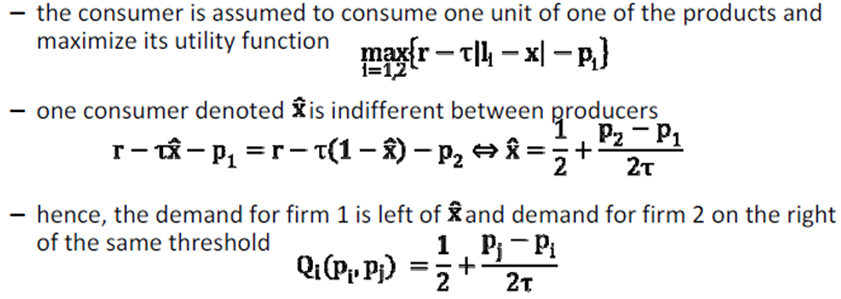
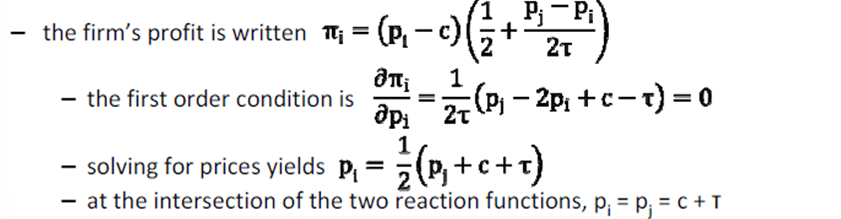
Due to product differentiation, equilibrium P > MC:

→ Each firm faces D fct that ≠ perfectly elastic

→ Producers of more differentiated products (higher τ) enjoy higher price-cost margins

Proof - (2) Location choice in differentiated product market

Assume 2 firms ≠ choose P BUT choose location:

Model describes industries in which P = regulated (p*), but firms choose non-P aspects of their product offer

• Mass 1 of consumers = assumed to have tastes uniformly distributed on interval [0,1]

• Indirect U fct of consumer located in x, consuming 1 unit of product i located

  l_i = v_i(x) = r - T |l_i - x| - p*

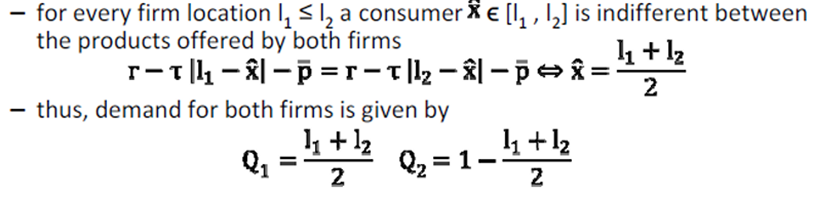
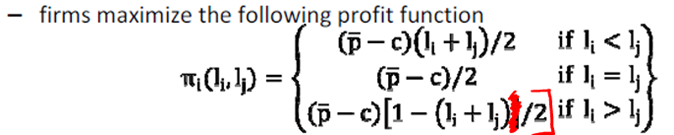
In unique NE of location game, both firms locate at center of support

• No firm has an incentive to deviate from this equilibrium, bc it would serve smaller proportion of market

• If firm 1 moves to the right, firm 2 has an incentive to also move to the right & serve larger proportion of market

This simple model shows that firms that have opportunity to differentiate their products, choose not to do so:

• From social perspective, total transport costs = minimized at locations ¼ & ¾

• Intro of competition ≠ improve welfare: If fixed production costs, customers better off with single firm

Proof - (3) P & location choice in differentiated product market (Part 1)

Firms simultaneously choose P & location

• Reservation value r for their ideal product, a mass 1 of consumers have tastes uniformly distributed on interval [0,1] & have U fct v_i(x) = r - T |l_i - x| - p*

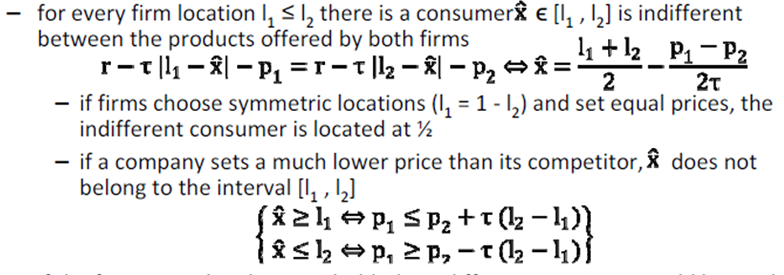
If first inequality ≠ hold, indifferent customer would be on left of l₁ or in other terms, also consumers on left of l₁ prefer good 2 to good 1

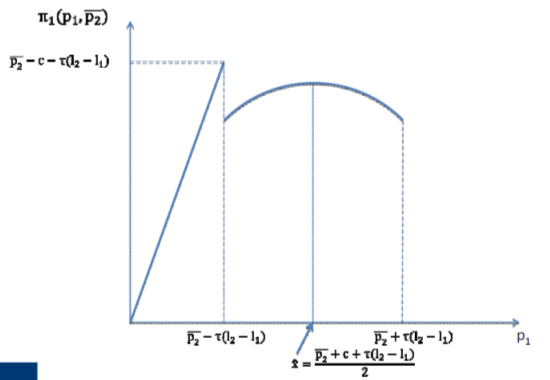
• There = non-linearity at P₁ = p₂ + T(l₂ - l₁)

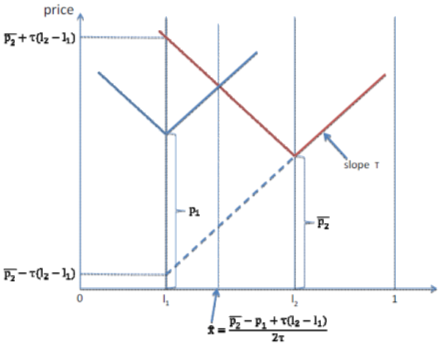
Proof - (3) P & location choice in differentiated product market (Part 2)

Profits = price-cost difference times demand:

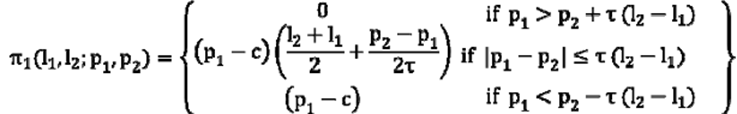
Profit fct shows downward jump when firm starts sharing market with producer of good 2

• Similarly, profit fct drops to 0, when no customer buys a good 1

Profit fct ≠ quasi-concave & has 2 local suprema

• First order approach can lead to errors

Locations ≠ necessarily at the extremes:

• Assuming that prices = such that the indifferent buyer belongs to

• For l₁ = l₂ unique P equilib = p₁ = p₂ = c

• Other P equilibria exist, but it can be demonstrated that, in dynamic setting, firms have a tendency to move closer to one another (offer closer substitutes) to increase D, which leads to instability in competition

Proof - (3) P & location choice in differentiated product market (Part 3)

The subgame perfect equilibrium (SPE) of the 2-stage game with quadratic transportation costs, firm choose l*₁ = 0 & l*₂ = 1

• With quadratic transportation costs, firms seek differentiate their product offerings in order to build some monopoly power vis-à-vis consumers located in their vicinities

In general, there are always 2 forces at play:

• Competition effects drives firms apart in order to increase product differentiations & raise market power

• Market size effect brings firms closer & reduces product differentiation  

VERTICALLY product differentiation - Definition

• When consumer groups agree on relative value of products, bc different q of desirable characteristic = embedded in product

Ex.: CPU (GHz), RAM (Mo), size screen of weight for laptops, l/100km or CO²g/km for cars, ABS, air conditioning, horsepower

VERTICALLY product differentiation - Firm perspective (Part 1)

Products = vertically differentiated, when consumer groups agree on the relative value of products

→ products = different qualities

Quality = described by a number : s_i ∈ [▁s,s ̅ ] ⊂ R⁺

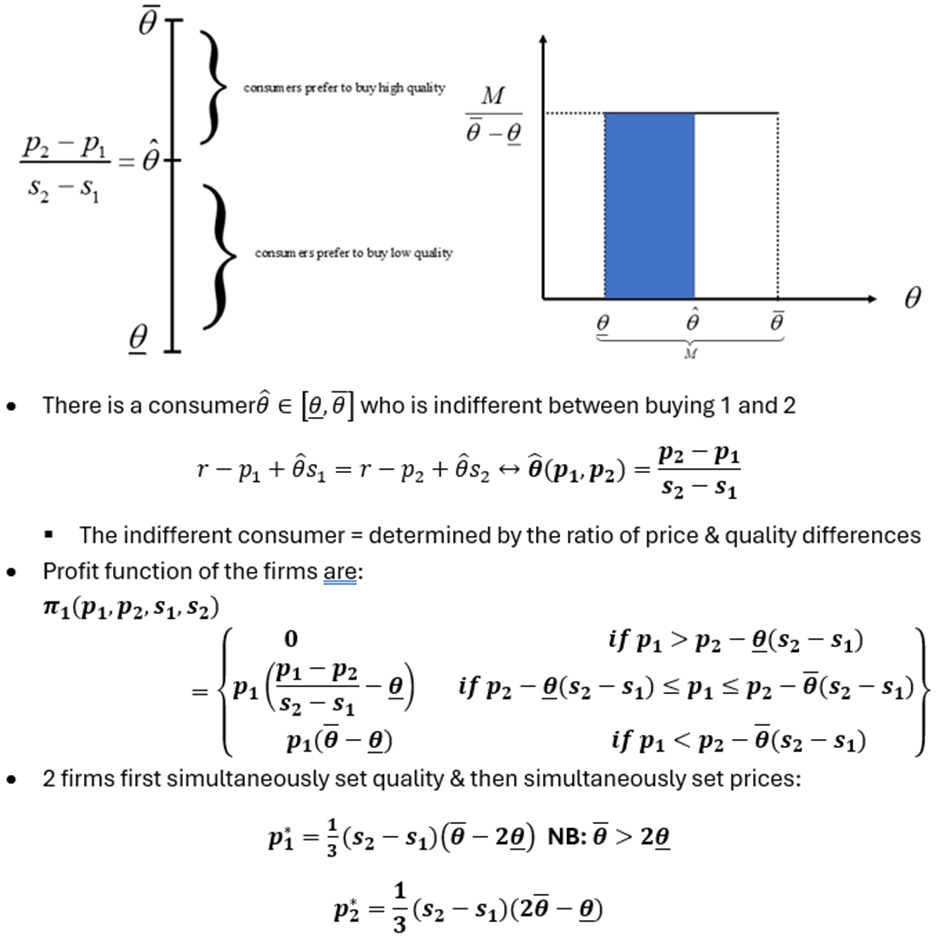
• Consumers agree: high quality = better than low, but differ in intensity of their preferences → θ ∈ [▁θ,θ ̅ ] ⊂ R⁺

• θ = uniformly distributed on its support & consumers = of mass M = θ ̅ - ▁θ

Consumer’s U fct:

• u₁ = q₀ + θ(s₁ - s ̅ )

• with outside option u₀ = q₀ - r - θs ̅ &

• budget constraint y = r + θs ̅

Consumers choose whether to buy product maximizing:

v(p, y ; θ)=max⁡[0, max((r - p₁ + θs₁)]

2 firms = assumed to have 0 MC (independent of quality) but firm 2 produces higher quality good s₁ < s₂ & set P below r(p₁, p₂ < r)

VERTICALLY product differentiation - Firm perspective (Part 2)

Equilibrium P only depend on quality differences:

→ Not only P of high quality firm increase with quality difference

BUT P of low quality firm also increases with quality difference (which = more surprising & due to assumption that all consumers buy in market)