Pchem 2 exam 1 vocab (ch 1, 2, 3, 4)
0.0(0)
Card Sorting
1/110
Earn XP
Description and Tags
kms
Last updated 2:32 PM on 2/16/23
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
111 Terms
1
New cards
Classical Physics
the study of the laws of nature that describe the motion and behavior of objects under normal circumstances, without taking into account the effects of quantum mechanics or relativity. predates modern, more complete, or more widely applicable theories.
2
New cards
Blackbody
absorbs and emits all frequencies, called an ideal body. serves as an idealization for any radiating material
3
New cards
Blackbody Radiation
the thermal electromagnetic radiation within, or surrounding, a body in thermodynamic equilibrium with its environment, emitted by a black body.
4
New cards
Boltzmann constant
k(B). 1.380649 × 10-23 m^2 kg s^-2 K^-1
5
New cards
Rayleigh-Jeans law
Expression derived in classical physics for the plot of the intensity of blackbody radiation versus frequency for several temperatures.
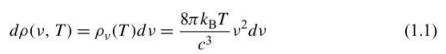
6
New cards
ultraviolet catastrophe
Note that the Rayleigh- Jeans law reproduces the experimental data at low frequencies. At high frequencies, however, the Rayleigh- Jeans law predicts that the radiant energy density diverges as v^2.
the frequency increases as the radiation enters the ultraviolet region. Failure of classical physics.
the frequency increases as the radiation enters the ultraviolet region. Failure of classical physics.
7
New cards
Planck constant
6\.62607015 × 10^-34 m^2 kg / s
8
New cards
Planck distribution law for blackbody radiation
Derived to solve the issue w Rayleigh-Jeans law for blackbodies, because it doesnt diverge at large frequencies
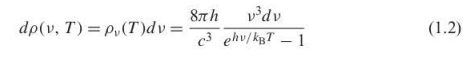
9
New cards
Wien displacement law
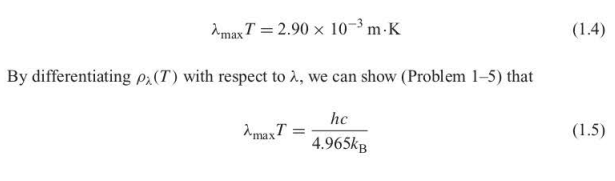
10
New cards
Stefan-Boltzmann law

11
New cards
Stefan-Boltzmann constant
sigma. 5.6697 x 10^-8 J m^-2 K^-4 s^-1
12
New cards
photoelectric effect
The ejection of electrons from the surface of a metal by radiation. German physicist Heinrich Hertz discovered that ultraviolet light causes electrons to be emitted from a metallic surface. experimental observations of the photoelectric effect are in stark contrast with the classical wave theory of light. Experimentally, the kinetic energy of the ejected electrons is independent of the intensity of the incident radiation.
13
New cards
threshold frequency
v(0). characteristic of the metallic surface, below which no electrons are ejected, regardless of the intensity of the radiation. Above v0, the kinetic energy of the ejected electrons varies linearly with the frequency v. These observations served as an embarrassing contradiction of classical theory.
14
New cards
photons
Einstein proposed instead that the radiation itself existed as small packets of energy, E = hv
15
New cards
work function
circle crossed through symbol. of a metal, is analogous to an ionization energy of an isolated atom.
16
New cards
kinetic energy
Einstein derived

17
New cards
derivations from einstein’s kinetic energy
shows that a plot of KE versus v should be linear and that the slope of the line should be h (plancks constant)
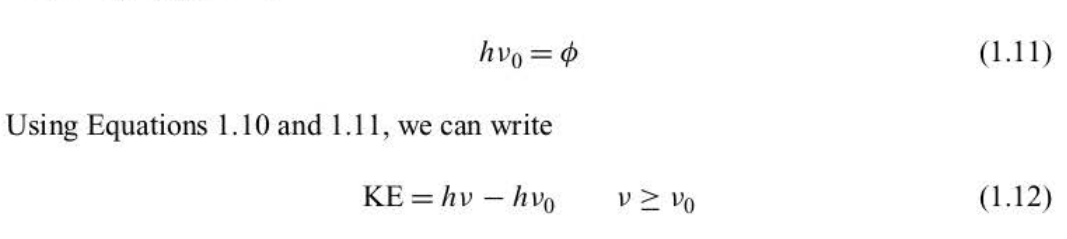
18
New cards
eV conversion
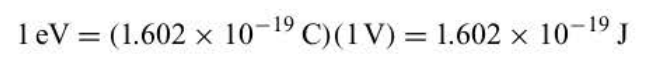
19
New cards
molar gas constant
R, 8.314 J K^-1 mol^-1
20
New cards
mechanical vibrations
of atoms, are subject to quantization. Einstein assumed that the oscillations of the atoms about their equilibrium lattice positions are quantized according to the formula e = nhv or delta e = hv.
21
New cards
law of Dulong and Petit
law states that the specific heat of an atomic solid times the atomic mass is approximately 25 J. A more fundamental, but equivalent, version of the law says that the molar heat capacity at constant volume, C(v), is equal to 3R, where R is the molar gas constant. The classical result is seen to occur at high temperatures, but C(v) decreases and goes to zero as the temperature is lowered. These low-temperature heat capacities are quite contrary to classical theory.
22
New cards
line spectra
every atom, when subjected to high temperatures or an electrical discharge, emits electromagnetic radiation of characteristic frequencies. each atom has a characteristic emission spectrum that consists of only certain discrete frequencies
23
New cards
wave number
The standard units used in spectroscopy. cm- 1
24
New cards
Balmer ‘s formula
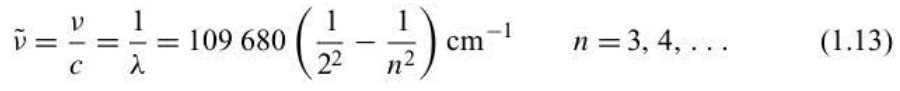
25
New cards
Balmer series
This series of lines, the ones occurring in the visible and near ultraviolet regions of the hydrogen atomic spectrum and predicted by Balmer's formula
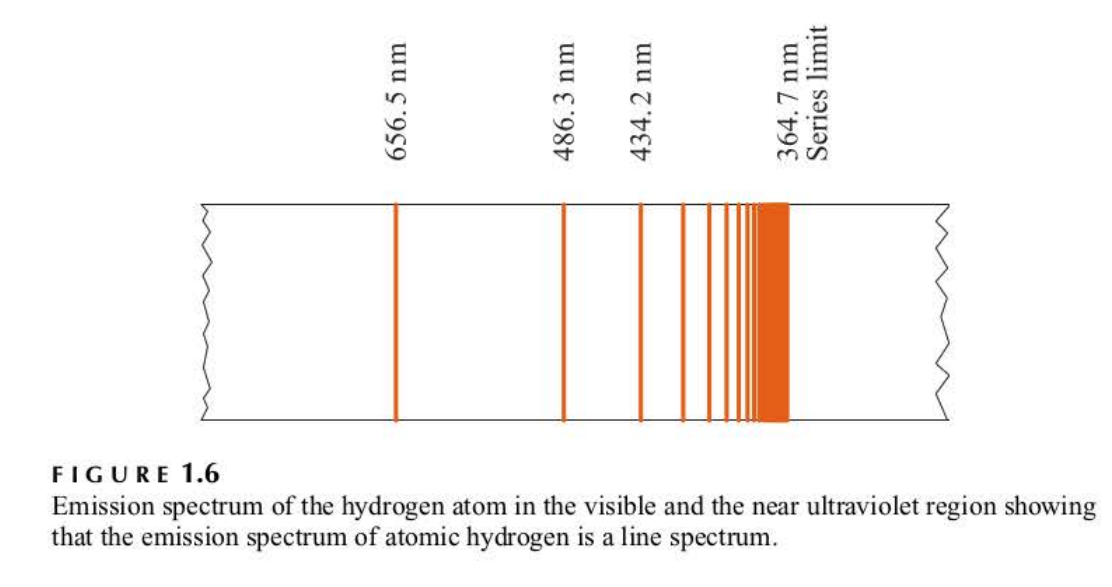
26
New cards
series limit
aka wavelength = 364.7 nm
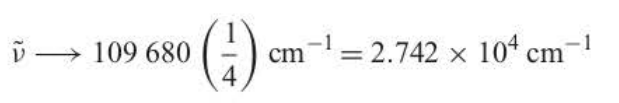
27
New cards
Lyman

28
New cards
Balmer
n1, n2, region of spectrum
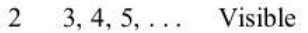
29
New cards
Paschen
n1, n2, region of spectrum. The term "near infrared" denotes the part of the infrared region of the spectnun that is near to the visible region.

30
New cards
Brackett
n1, n2, region of spectrum.

31
New cards
Rydberg formula
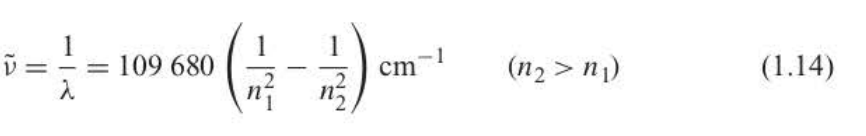
32
New cards
Rydberg constant
R(H). 109,677.57 cm^-1.
33
New cards
Ritz combination rule
describes the relationship of the spectral lines for all atoms. it is possible to find pairs of spectral lines, which have the property that the sum of their wavenumbers is also an observed spectral line.
34
New cards
The kinetic energy of the revolving particle
T = KE
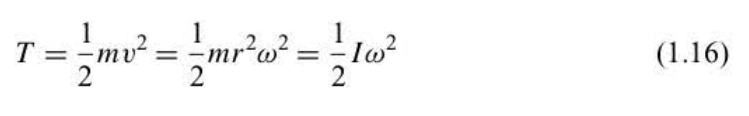
35
New cards
moment of inertia
I = mr^2
36
New cards
Linear momentum
p = mv. fundamental quantity in linear systems
37
New cards
angular momentum
fundamental quantity associated with rotating systems

38
New cards
The Correspondences Between the Motion of Linear Systems and Rotating Systems
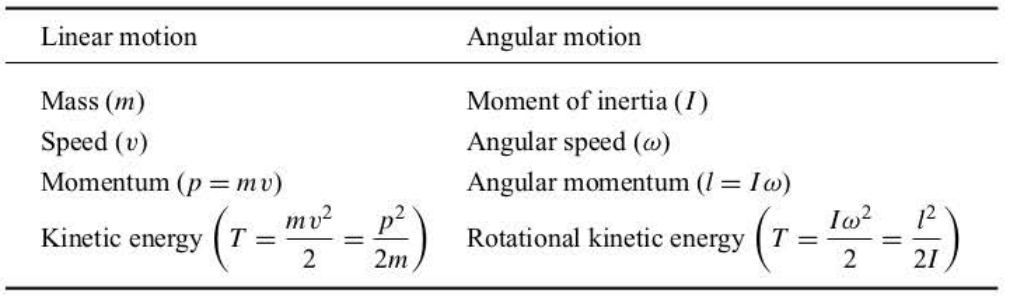
39
New cards
ground-state energy
the state of lowest energy, n=1
40
New cards
excited slates
states of higher energy, n=2+. generally unstable with respect to the ground state
41
New cards
Bohr frequency condition
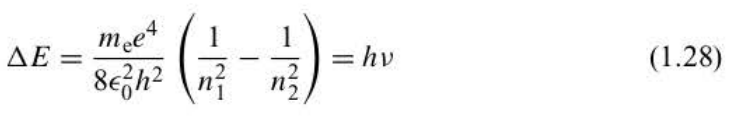
42
New cards
Bohr frequency condition in the form of the empirical Rydberg formula
hv = hcv with \~ above the v
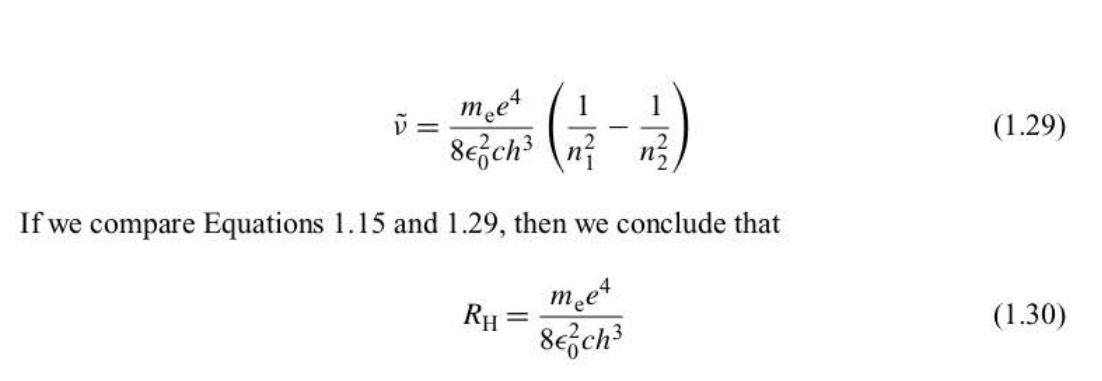
43
New cards
reduced mass µ
can be used in the rydberg constant for m(e)

44
New cards
Bohr frequency condition for non-hydrogen-like atoms
hydrogen-like ion = He^+ Li^2+ Be^3+
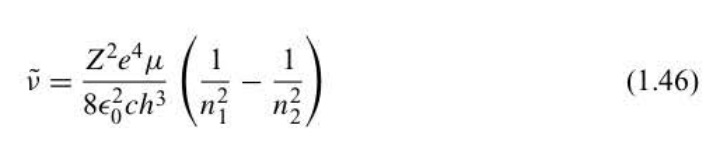
45
New cards
wave-particle duality of light
light appears wavelike in some instances and particle-like in others
46
New cards
De Broglie wavelength
also written to = h/p
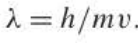
47
New cards
The de Broglie Wavelengths of Various Moving Objects
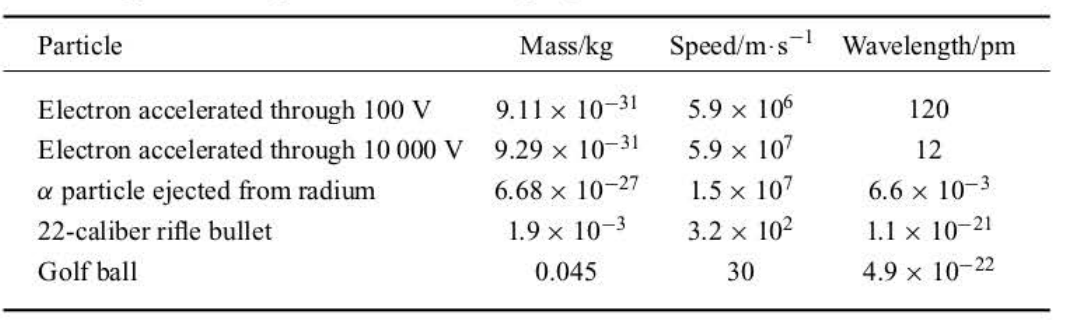
48
New cards
quantum condition

49
New cards
Bohr quantization condition

50
New cards
X-ray diffraction
When a beam of X rays is directed at a crystalline substance, the beam is scattered in a definite manner characteristic of the atomic structure of the crystalline substance. occurs because the interatomic spacings in the crystal are about the same as the wavelength of the X rays.
51
New cards
light and matter
have the characteristics of both waves and particles
52
New cards
Heisenberg’s uncertainty principle
states that if we wish to locate any particle to within a distance delta x, then we automatically introduce an uncertainty in the momentum of the particle and that the uncertainty is given by the equation

53
New cards
Schrodinger equation
a differential equation whose solution, psi(x), describes a particle of mass m moving in a potential field described by V (x).
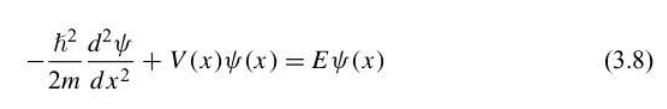
54
New cards
amplitude
The maximum displacement of something from its equilibrium horizontal position.
55
New cards
classical wave equation
let u(x, t) be the displacement of the string, then u (x , t) satisfies the equation. v is the speed with which a disturbance moves along the string

56
New cards
partial differential equation
n equation containing an unknown function of two or more variables and its partial derivatives with respect to these variables.
57
New cards
independent variable
a variable (often denoted by x ) whose variation does not depend on that of another.
58
New cards
linear partial differential equation
If the dependent variable and all its partial derivatives occur linearly in any partial differential equation (its derivatives appear only to the first power and there are no cross terms)
59
New cards
boundary conditions
specify the behavior of u(x, t) at the boundaries.
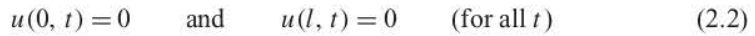
60
New cards
separation of variables
any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation
61
New cards
ordinary differential equations
an equation which is defined for one or more functions of one independent variable and its derivatives.
62
New cards
degeneracy

63
New cards
wave functions
solutions to the Schrodinger equation
64
New cards
stationary-state wave functions
Solutions to the time-independent Schrodinger equation
65
New cards
particle in a box
the time-independent Schrodinger equation applied to a free particle of mass m that is restricted to lie along a one-dimensional interval of length a.
66
New cards
spatial amplitude
of a wave
67
New cards
h-bar
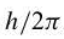
68
New cards
operator
a symbol that tells you to do something to whatever follows the symbol. i.e. dy/dx or d/dx, SQRT, integral symbol & dx, a constant in front of a value, etc. Denoted as the A in the image.
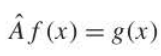
69
New cards
linear operators
c1 and c2 are constants. the picture shows a method that proves this
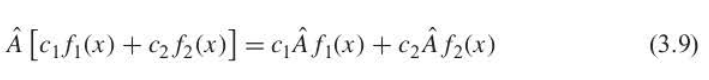
70
New cards
eigenfunction
in an eigenvalue equation, the function of an operator A and eigenvalue a

71
New cards
eigenvalue
The constant a

72
New cards
eigenvalue problem
Determining the function and constant of a given operator

73
New cards
Schrodinger equation as an eigenvalue problem

74
New cards
Hamiltonian operator
The wave function is an eigenfunction, and the energy is an eigenvalue of this. If V(x) = 0, the energy is all kinetic energy and can be defined as an operator T
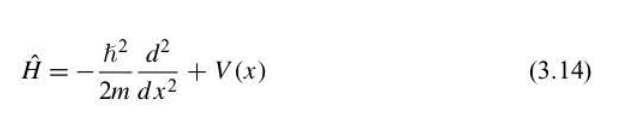
75
New cards
Kinetic energy operator

76
New cards
momentum operator
\
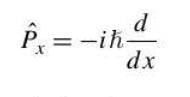
77
New cards
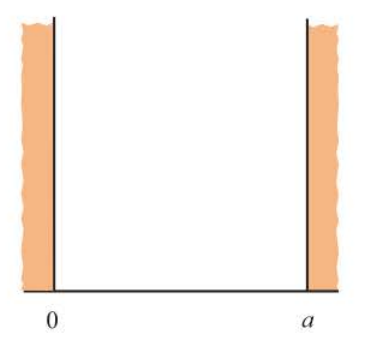
problem of a particle in a one-dimensional box
the case of a free particle of mass m constrained to lie along the x axis between x = 0 and x =a
78
New cards
free particle
experiences no potential energy. V (x) = 0. Equation in 1-D box
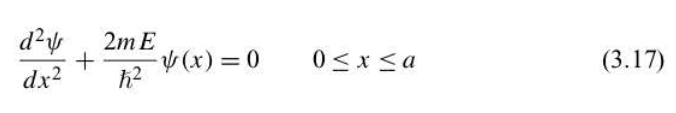
79
New cards
probability that the particle is located between x and x + dx
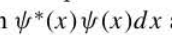
80
New cards
quantum number
integer n, seen in this equation and many others. related to excitement state of electrode

81
New cards
energy of a particle

82
New cards
The wave function corresponding to the energy of a particle
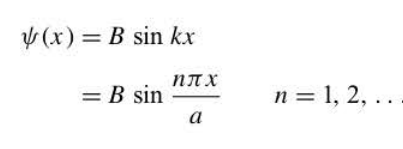
83
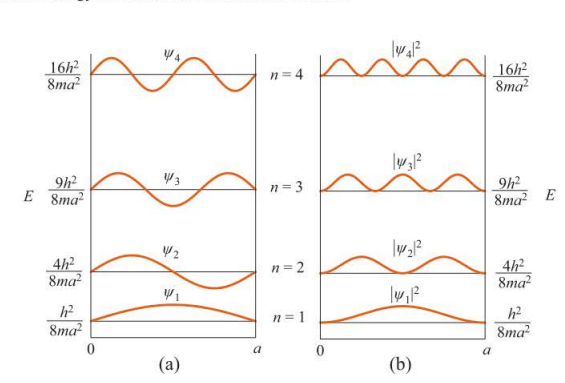
New cards
energy levels, wave functions (a), and probability densities (b) for the particle in a box
84
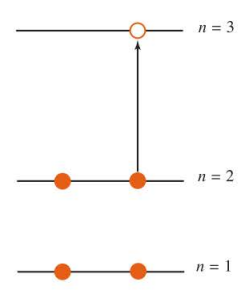
New cards
free-electron model energy-level scheme example
for butadiene
85
New cards
normalized wave function
satisfied this equation
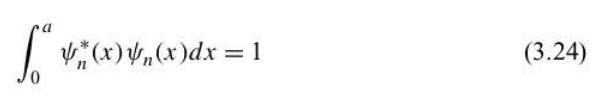
86
New cards
normalization. constant
the constant that multiplies a wave function is adjusted to assure that Equation 3.24 is satisfied

87
New cards
correspondence principle
quantum-mechanical results and classical-mechanical results tend to agree in the limit of large quantum numbers. the particle tends to behave classically in the limit of large n (fairly uniformly distributed). The large quantum number limit is often called the classical limit
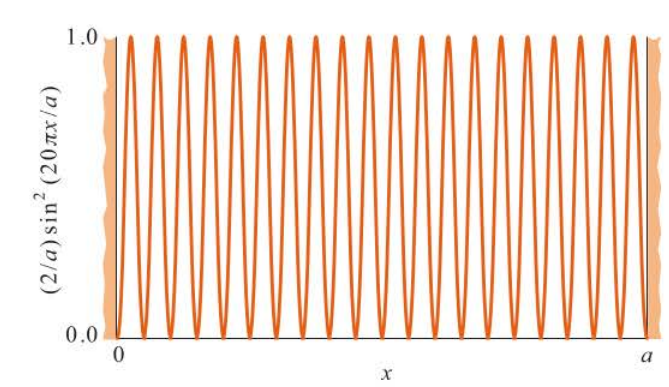
88
New cards
root-mean-square momentum
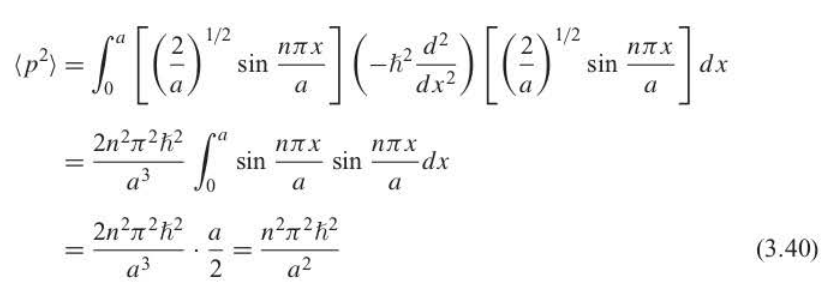
89
New cards
Heisenberg uncertainty principle

90
New cards
three-dimensional particle in a box
the particle is confined to lie within a rectangular parallelepiped with sides of lengths a, b, and c
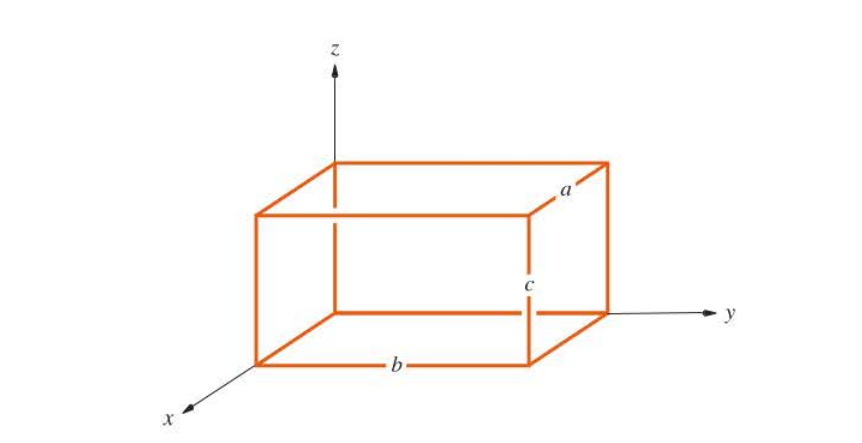
91
New cards
Schrodinger equation for a three-dimensional particle in a box

92
New cards
Laplacian operator
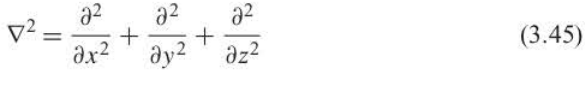
93
New cards
The energy levels for a particle in a cube, showing degeneracies

94
New cards
dynamical variables
quantities such as position, momentum, angular momentum, and energy
95
New cards
observable
A measurable dynamical variable
96
New cards
trajectory
The vector r (t) describes the position of the particle as a function of time, and is known as this property.
97
New cards
Postulate 1
The state of a quantum-mechanical system is completely specified by a function psi (r, t) that depends on the coordinates of the particle and on time. This function, called the wave function or state function, has the important property that psi\*(r, t)psi(r, t)dxdydz is the probability that the particle lies in the volume element dxdydz located at r at time t.

98
New cards
Postulate 2
To every observable in classical mechanics there corresponds a linear, Hermitian operator in quantum mechanics
99
New cards
Classical-Mechanical Observables and Their Corresponding Quantum-Mechanical Operators

100
New cards
Postulate 3
In any measurement of the observable associated with the operator A, the only values that will ever be observed are the eigenvalues a, which satisfy the eigenvalue equation