Geometry-Regents

undefined terms

point, line, plane

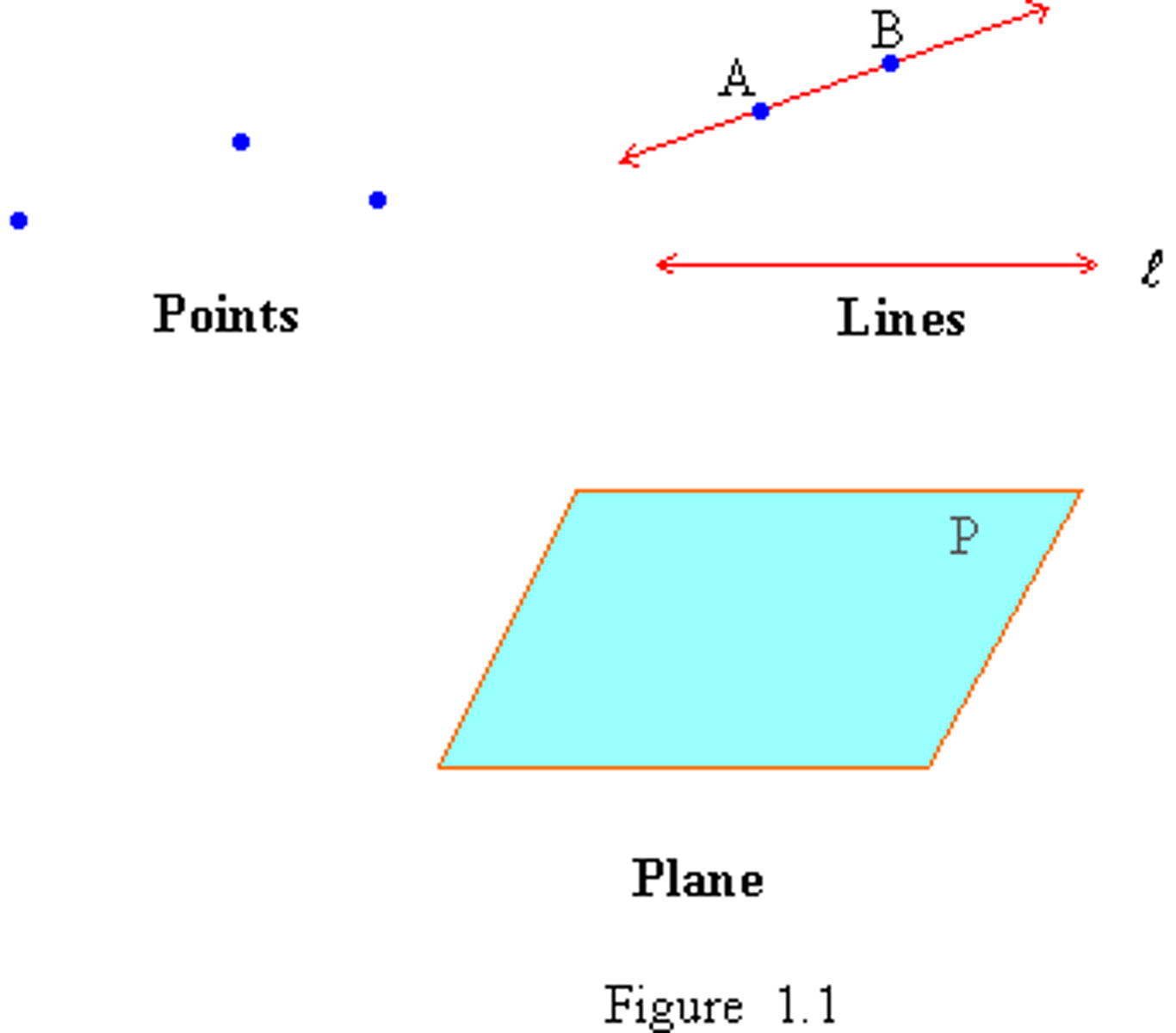
colinear points

points that lie on the same line

*notation for a point is a capital letter

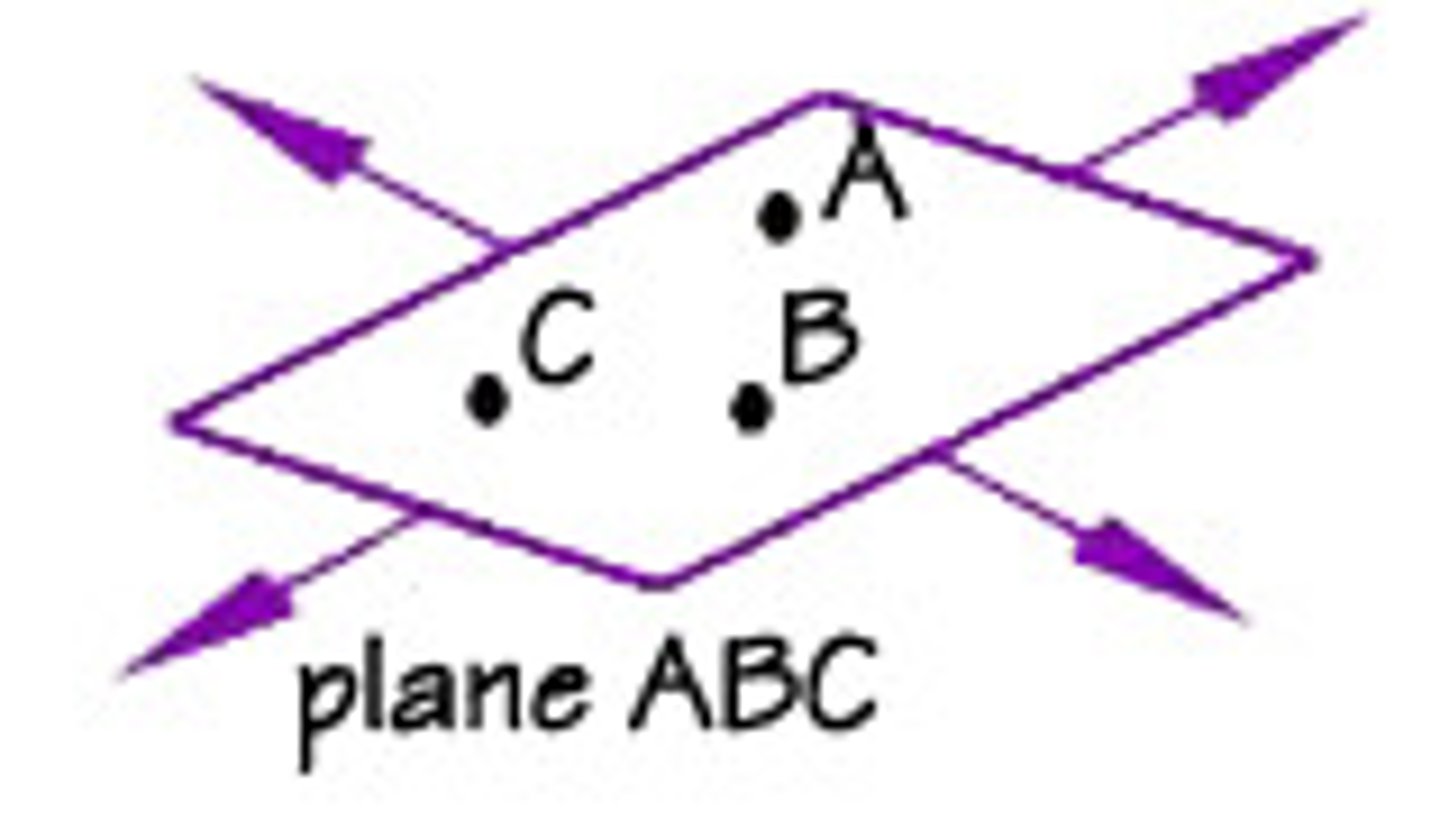
coplanar points

points that lie on the same plane

*notation for a point is a capital letter

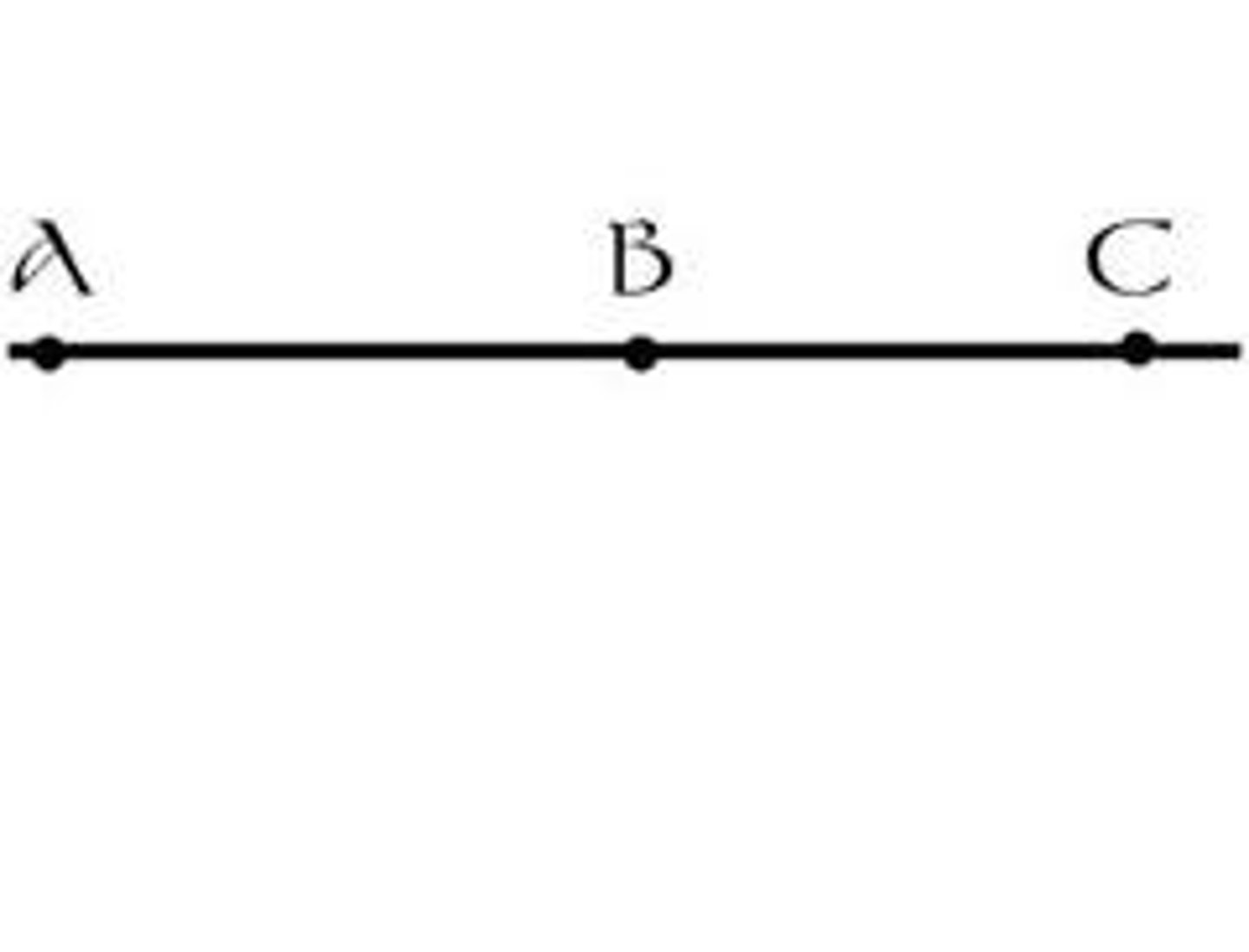
how many points are require to create a unique line?

2 points

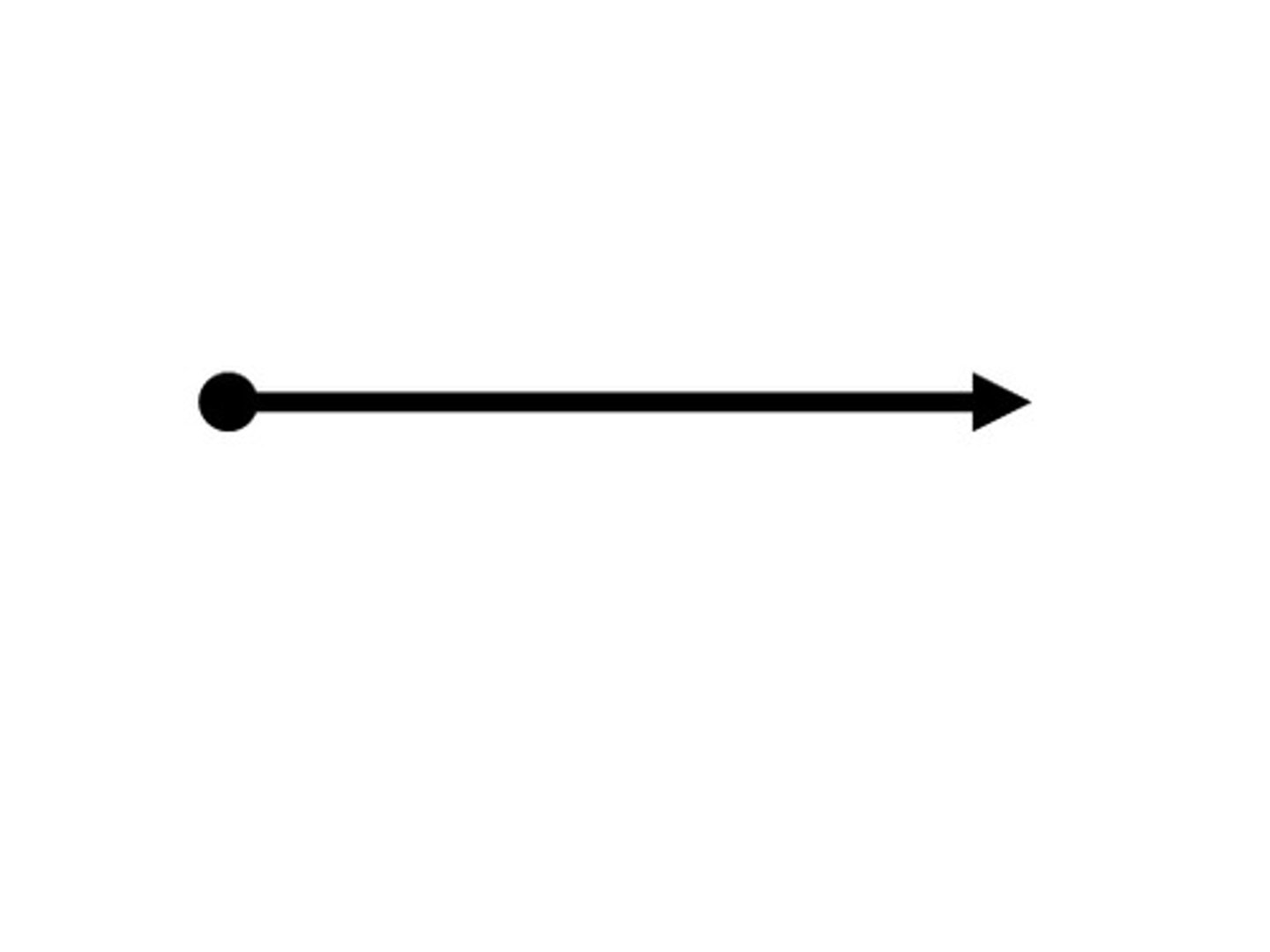
ray

a part of a line that starts at an endpoint and extends forever in one direction

line segments

Part of a line with two end points.

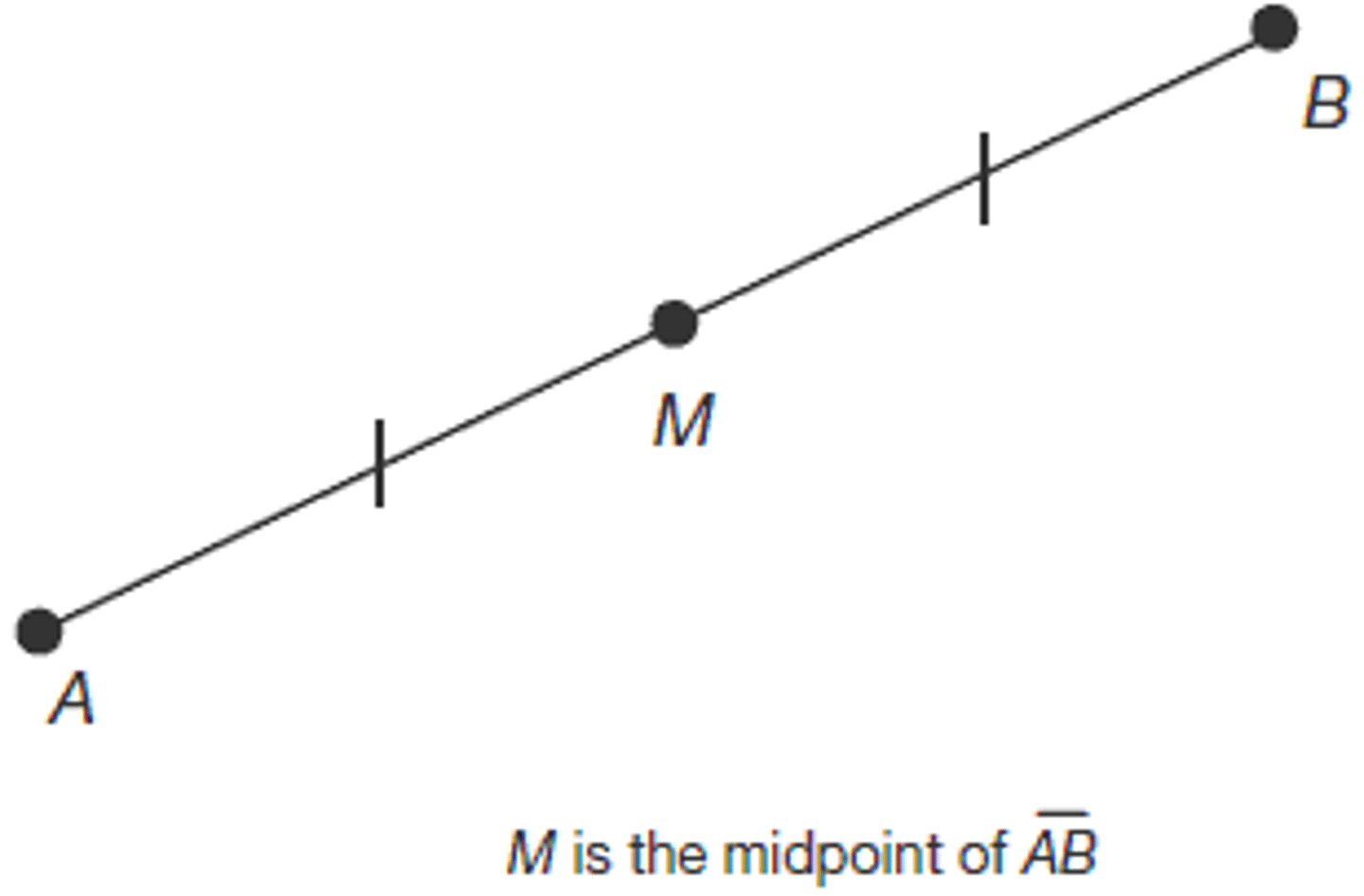
midpoint of a segment

A point that divides a segment into two congruent segments

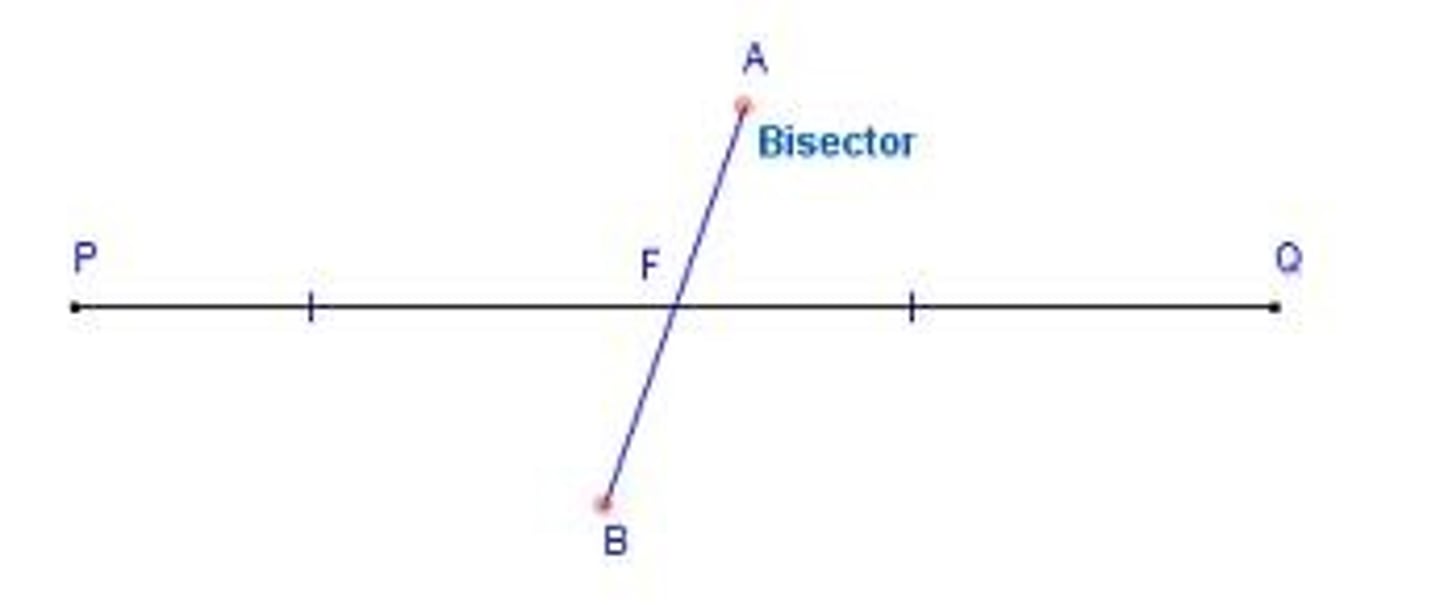
bisector of a segment

a line, segment, ray, or plane that intersects the segment at its midpoint

what is the difference between the bisector of a segment and the midpoint of a segment?

A bisector is a line or ray that goes through the midpoint.

(they co-exist)

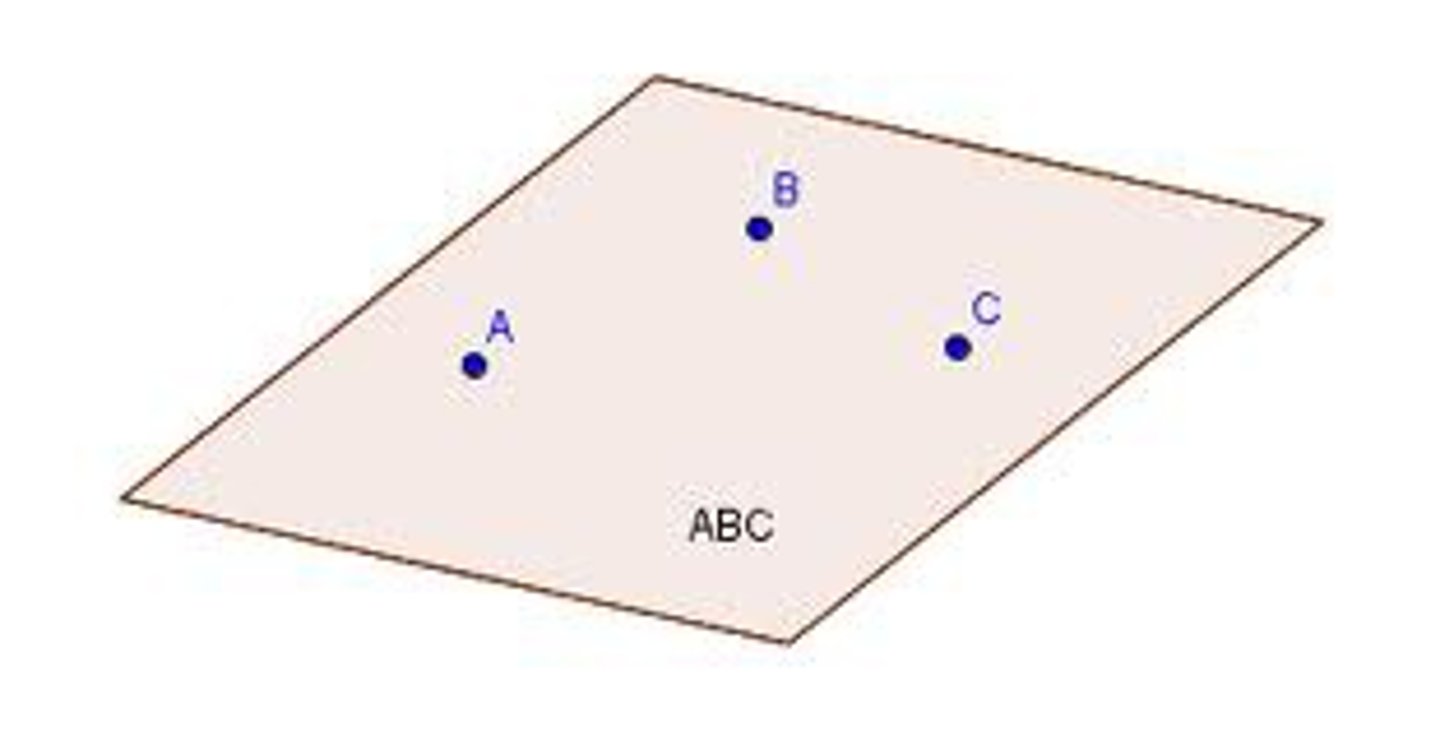
How many points are required to create a unique plane?

3

Congruence

Two objects that have the same size and shape

intersection

the set of points the figures have in common

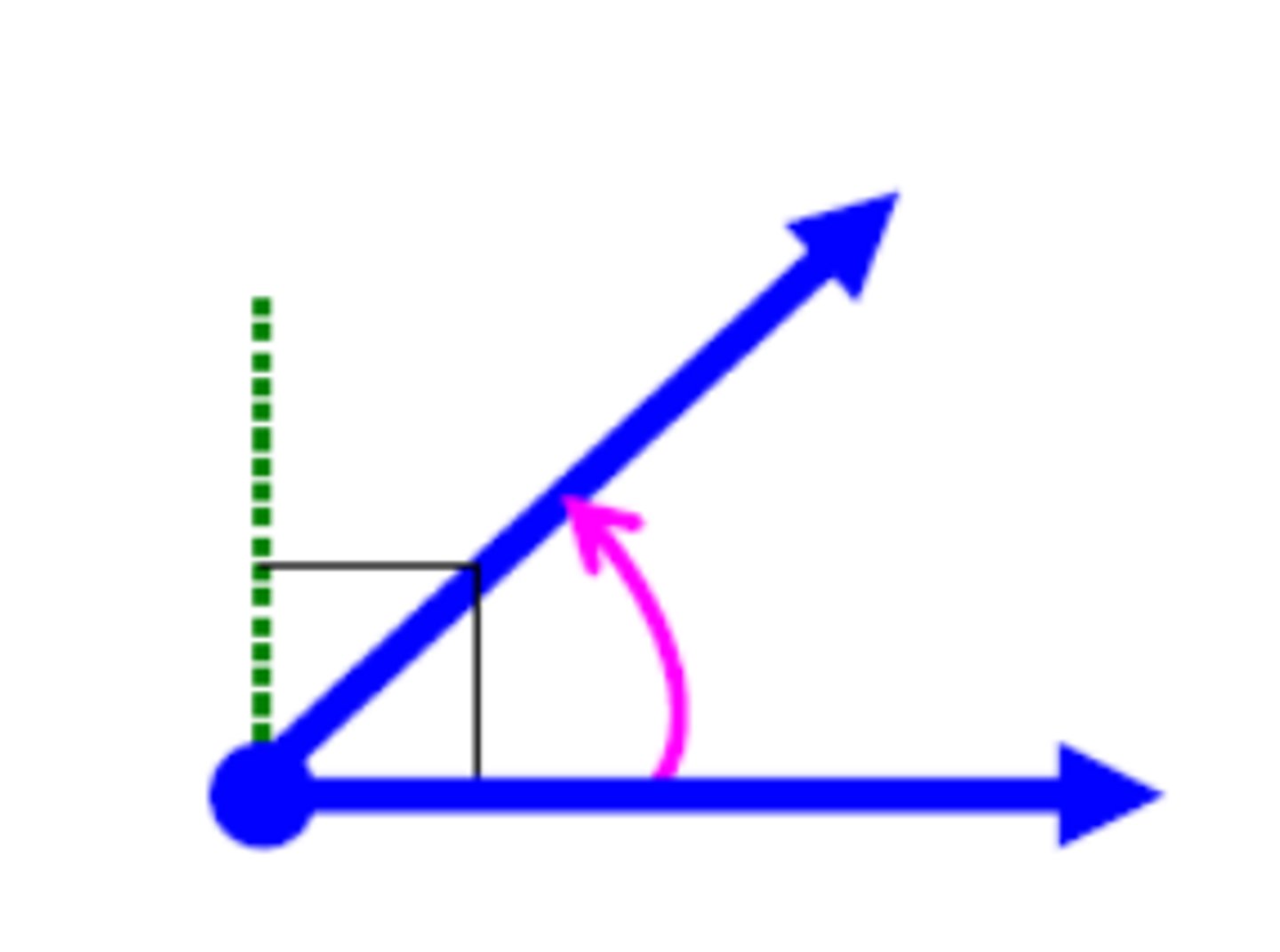
right angle

an angle that measures 90 degrees

(created by perpendicular lines) *have to write this in proof

acute angle

an angle that measures less than 90 degrees

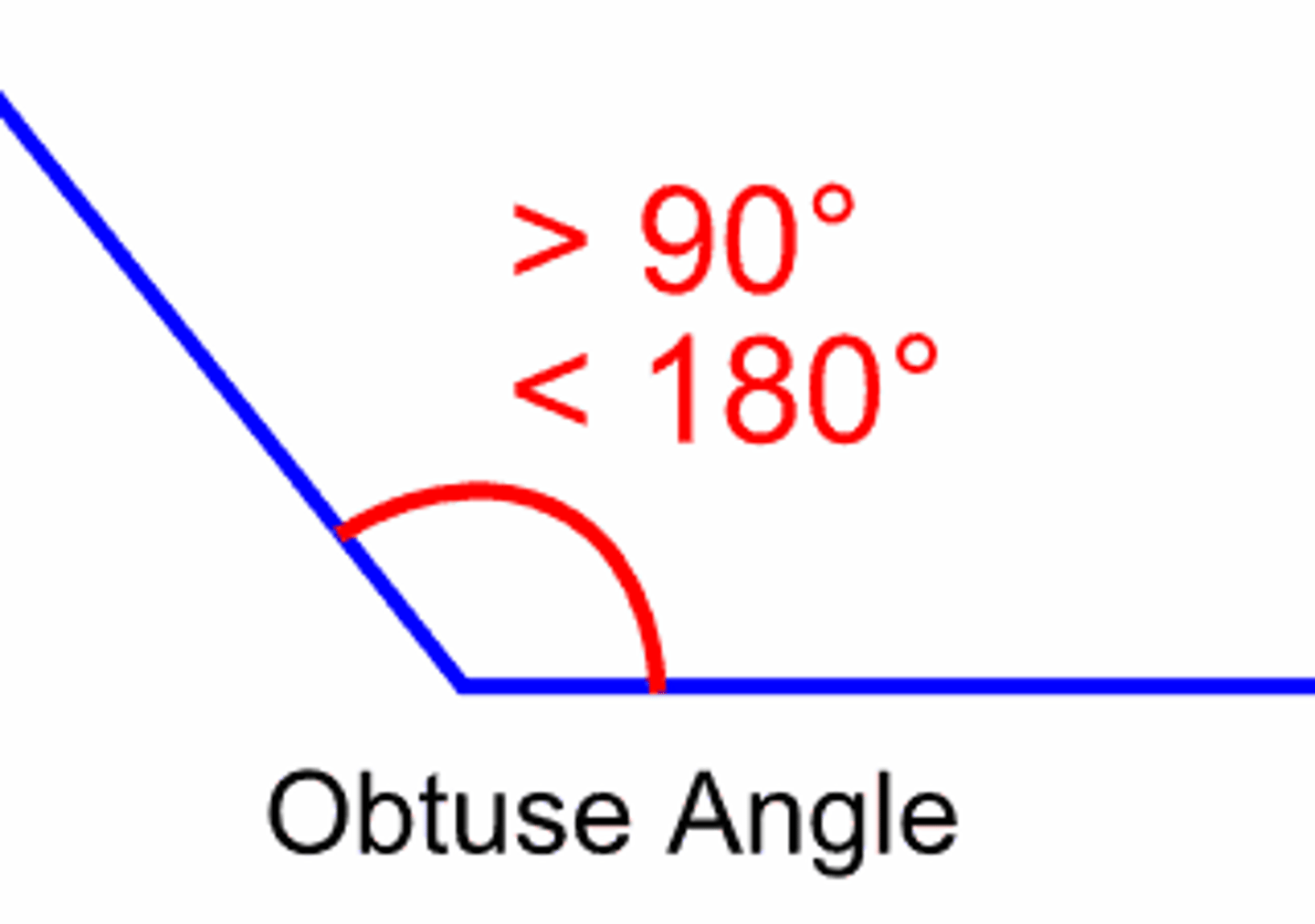
obtuse angle

An angle that measures more than 90 degrees but less than 180 degrees

congruent angles

angles that have the same measure

angle bisector

a ray that divides an angle into two congruent angles

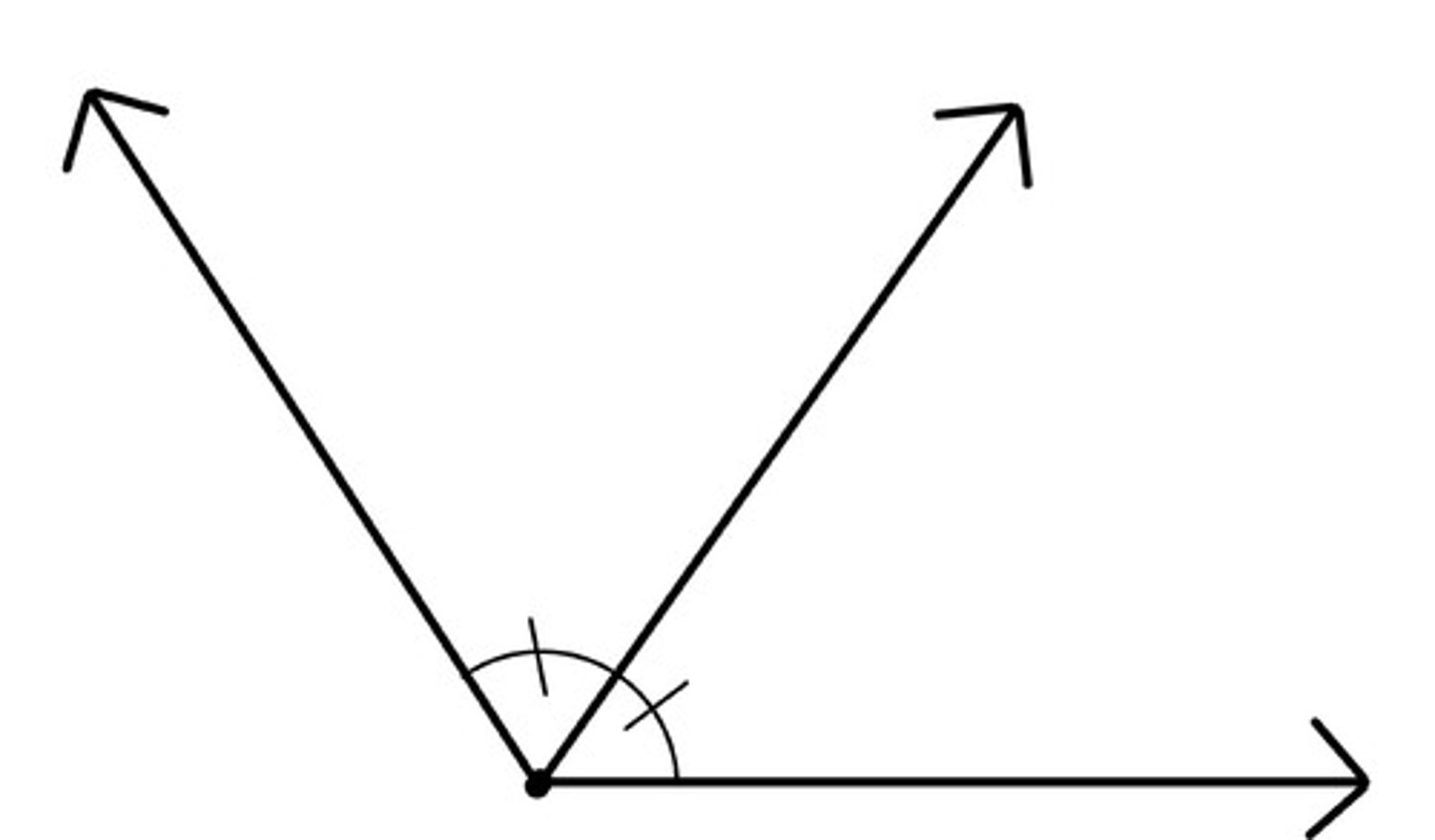
adjacent angles

Angles that have a common side and a common vertex (corner point).

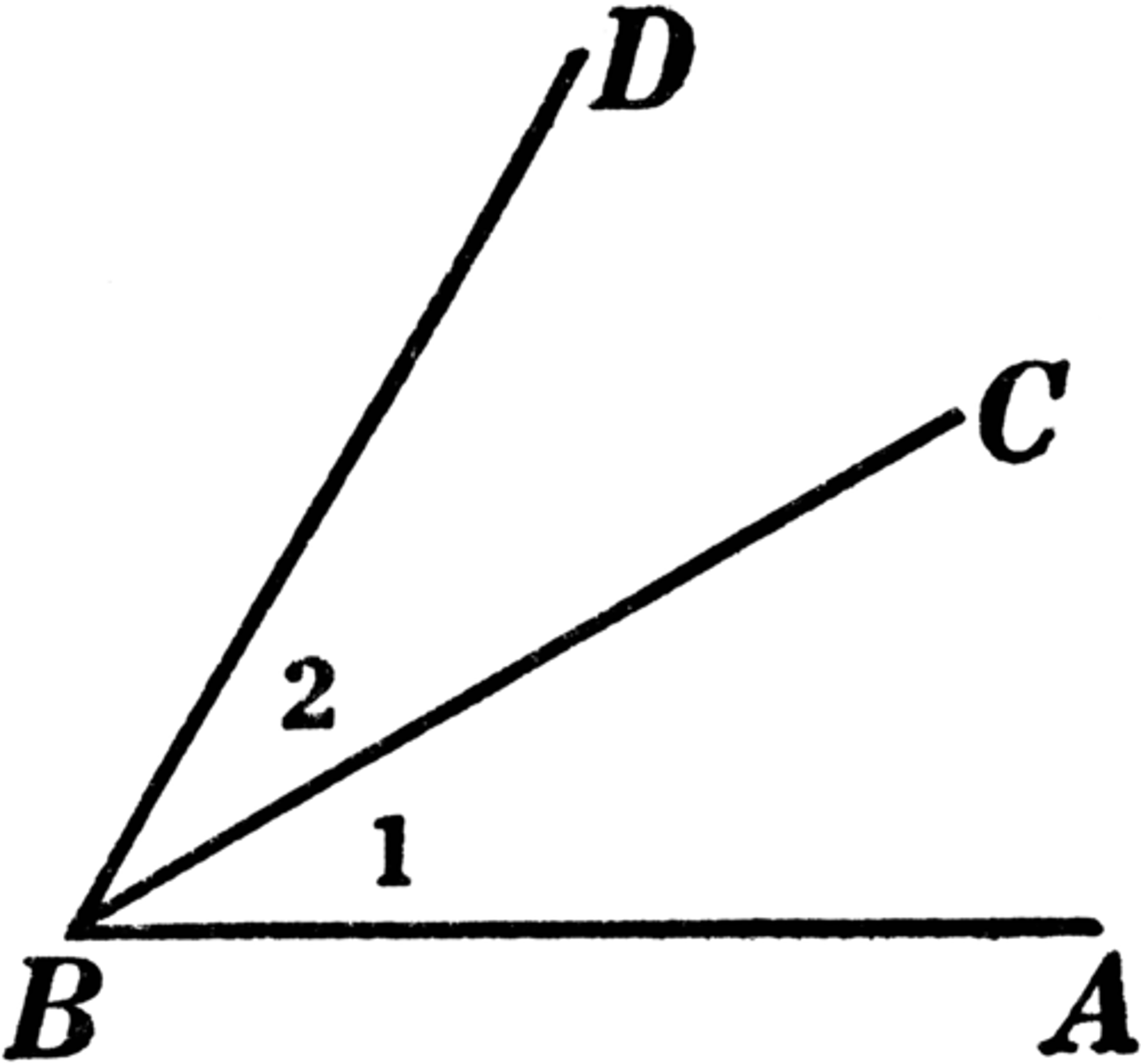
postulate

a statement that is accepted as true without proof

Theorem

a statement that can be proven

Addition Postulate

If equal quantities are added to equal quantities, the sums are equal.

if a = b and c = d then a + c = b + d

Subtraction Postulate

If equal quantities are subtracted from equal quantities, the differences are equal.

If a = b and c = d, then a-c = b-d

Multiplication postulate

If equal quantities are multiplied by equal quantities, the products are equal.

(also Doubles of equal quantities are equal.)

Division Postulate

If equal quantities are divided by equal nonzero quantities, the quotients are equal.

(also Halves of equal quantities are equal.)

Substitution Postulate

a quantity may be substituted for its equal in any statement of equality

If a = b but a = c, then c = b.

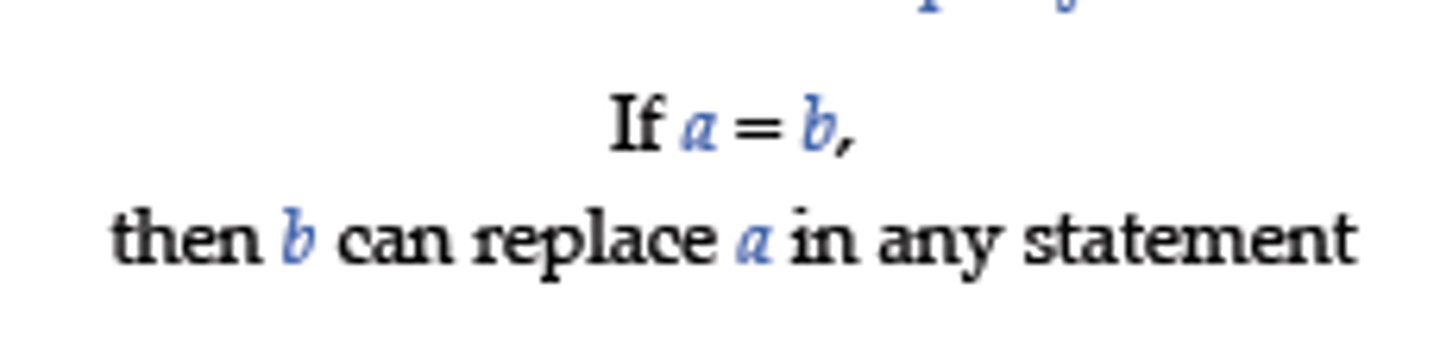
Partition Postulate

The whole is equal to the sum of its parts.

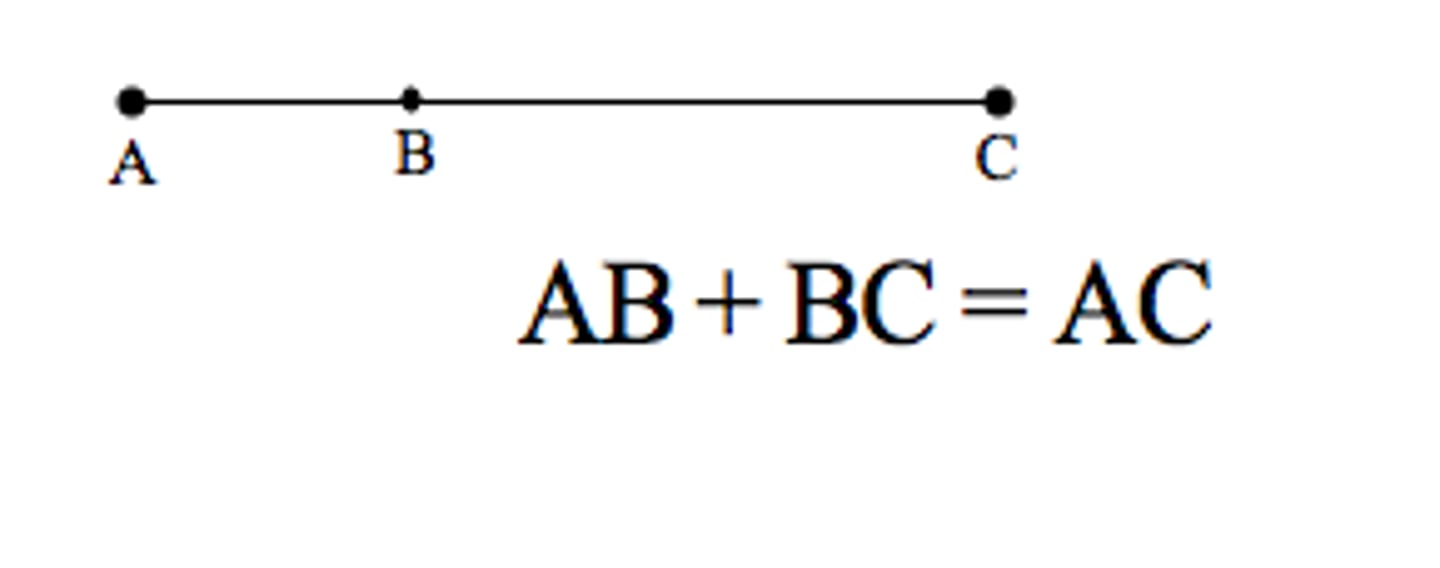
equivalence relation

a relation that is reflexive, symmetric, and transitive

Reflexive Property

A quantity is congruent (equal) to itself.

a = a

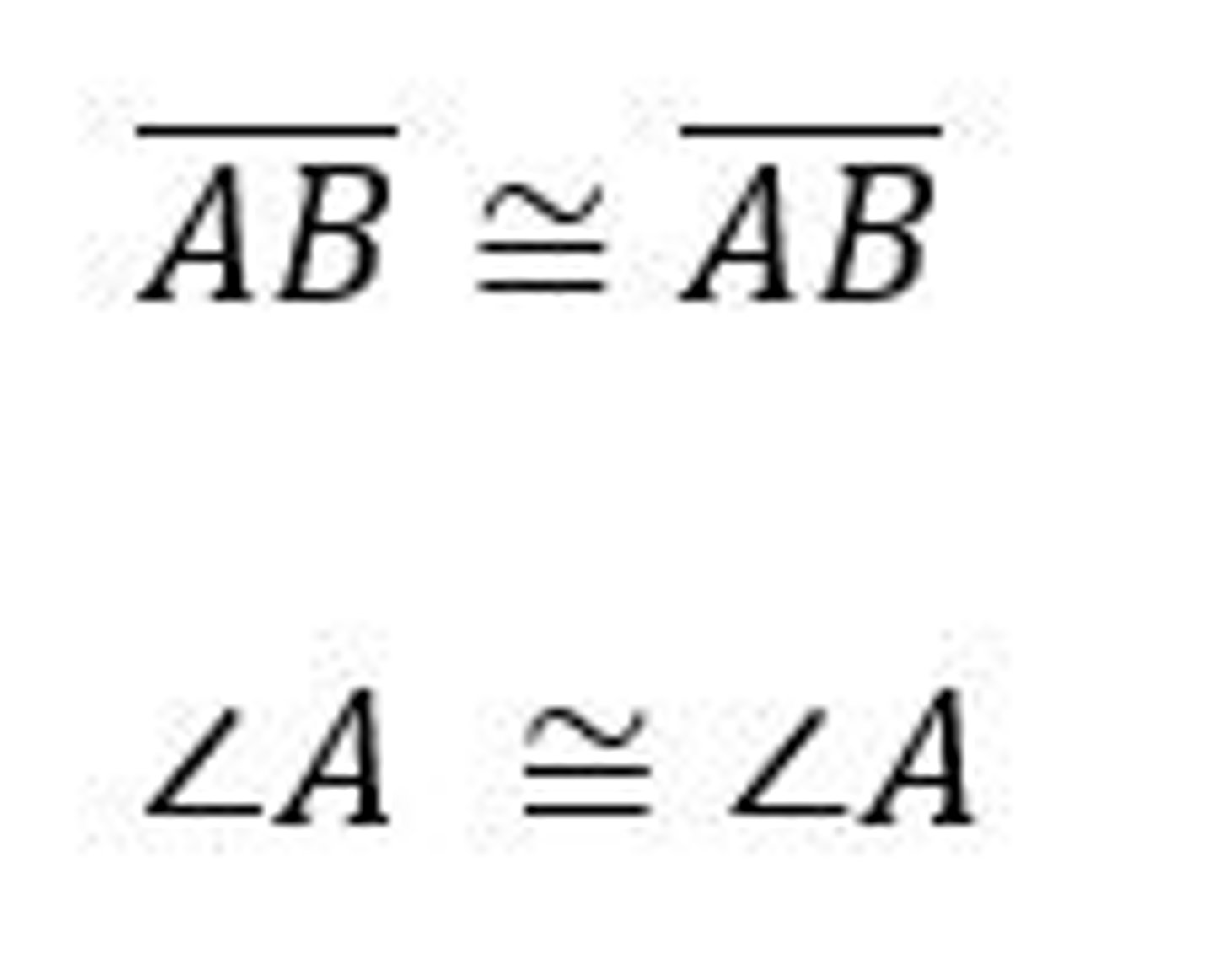
Symmetric Property

if a=b, then b=a

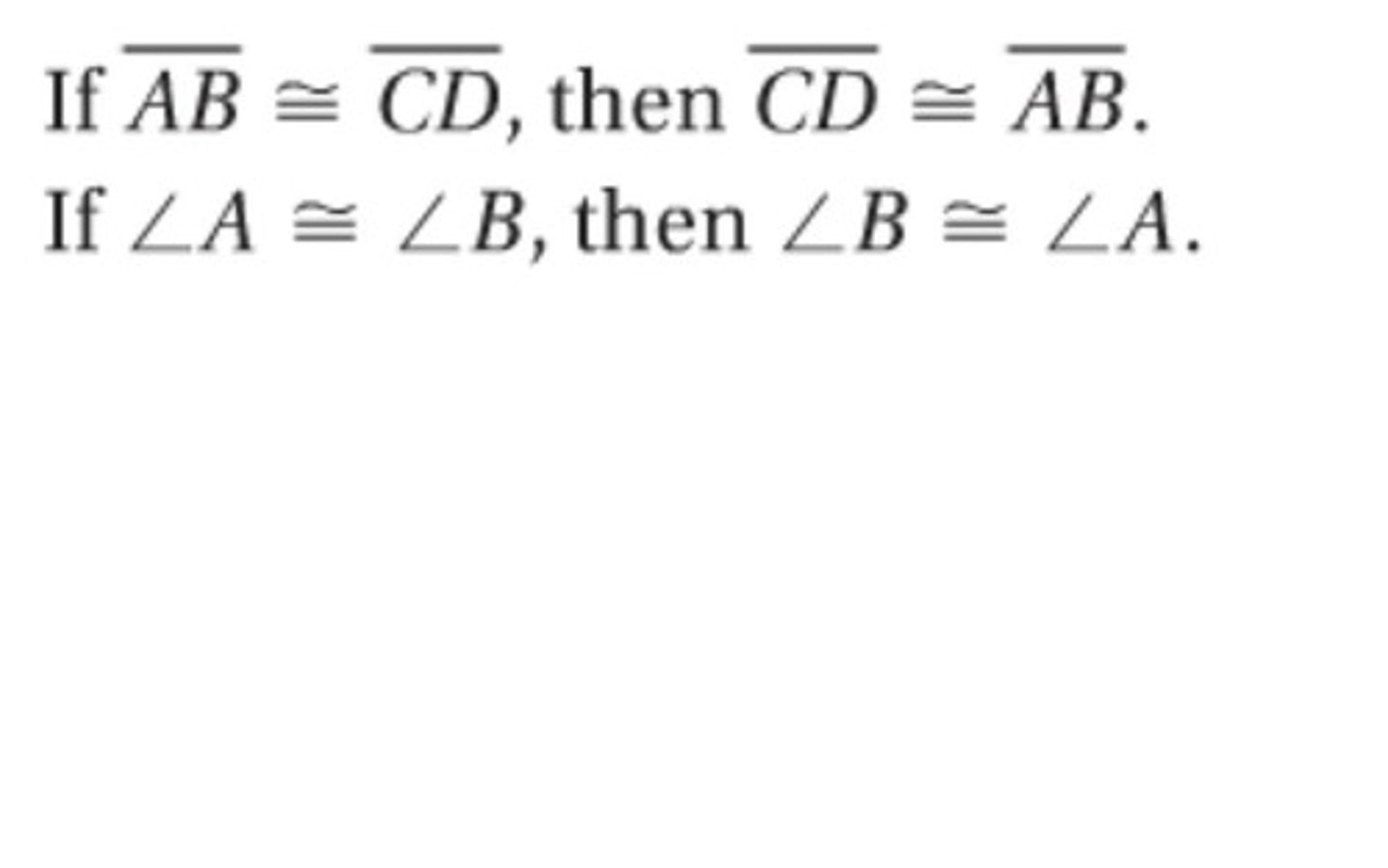
Transitive Property

If a=b and b=c, then a=c

*must be in order

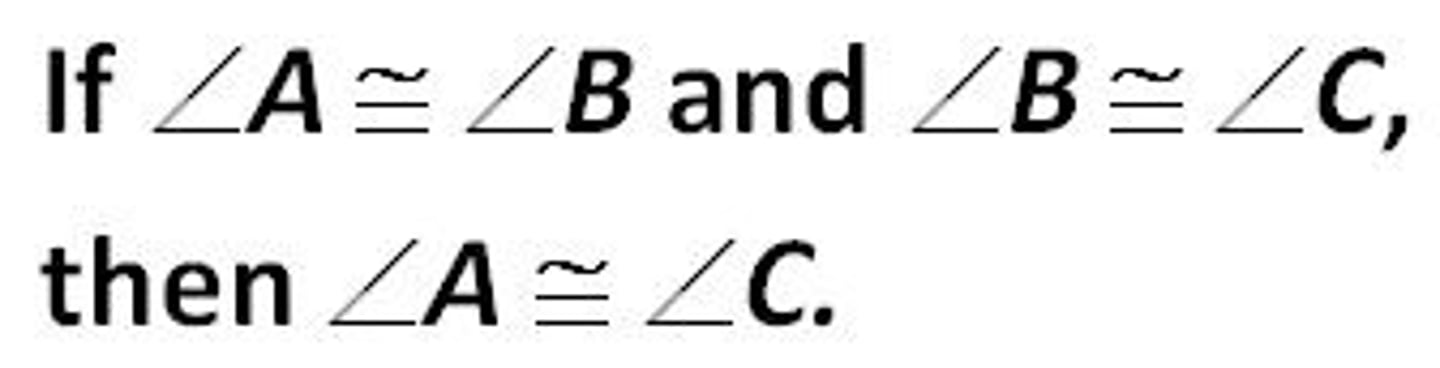
complimentary angles

two angles that add up to 90 degrees

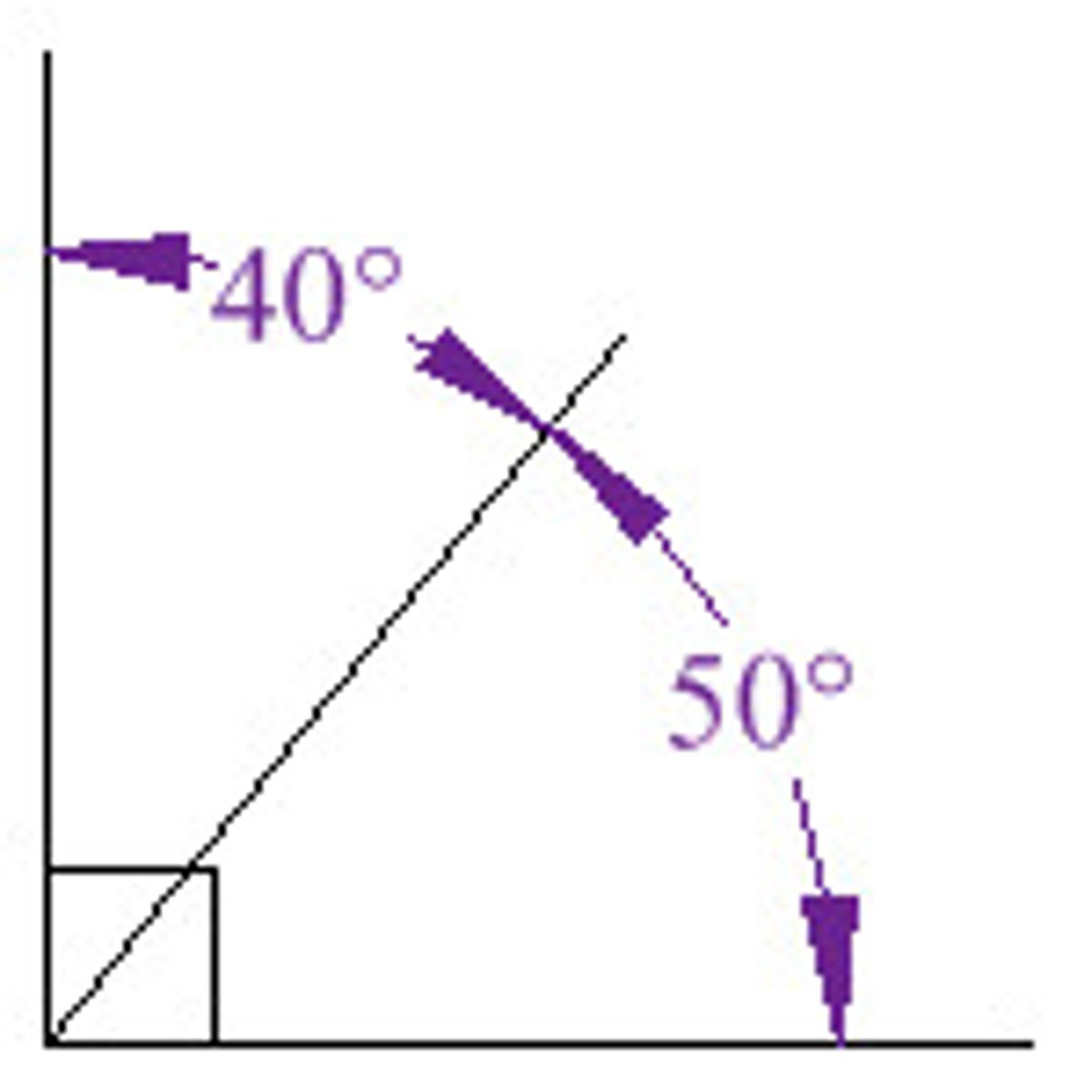
Suppplementary angles

Two angles whose sum is 180 degrees

vertical angles

A pair of opposite congruent angles formed by intersecting lines

- measures are equal

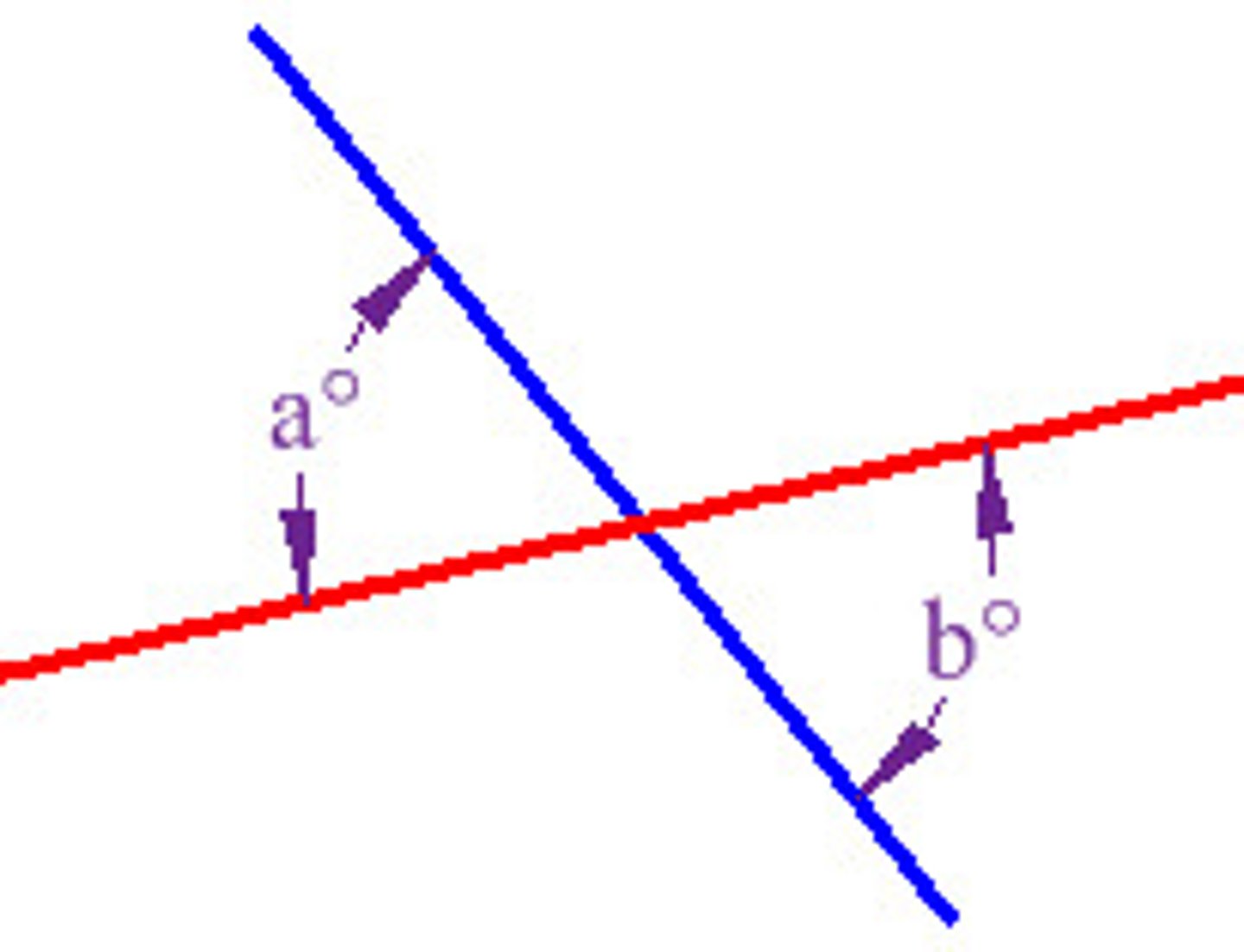
linear pair of angles

two adjacent angles whose sum is a straight angle

- the sum is always 180

-supplementary angles

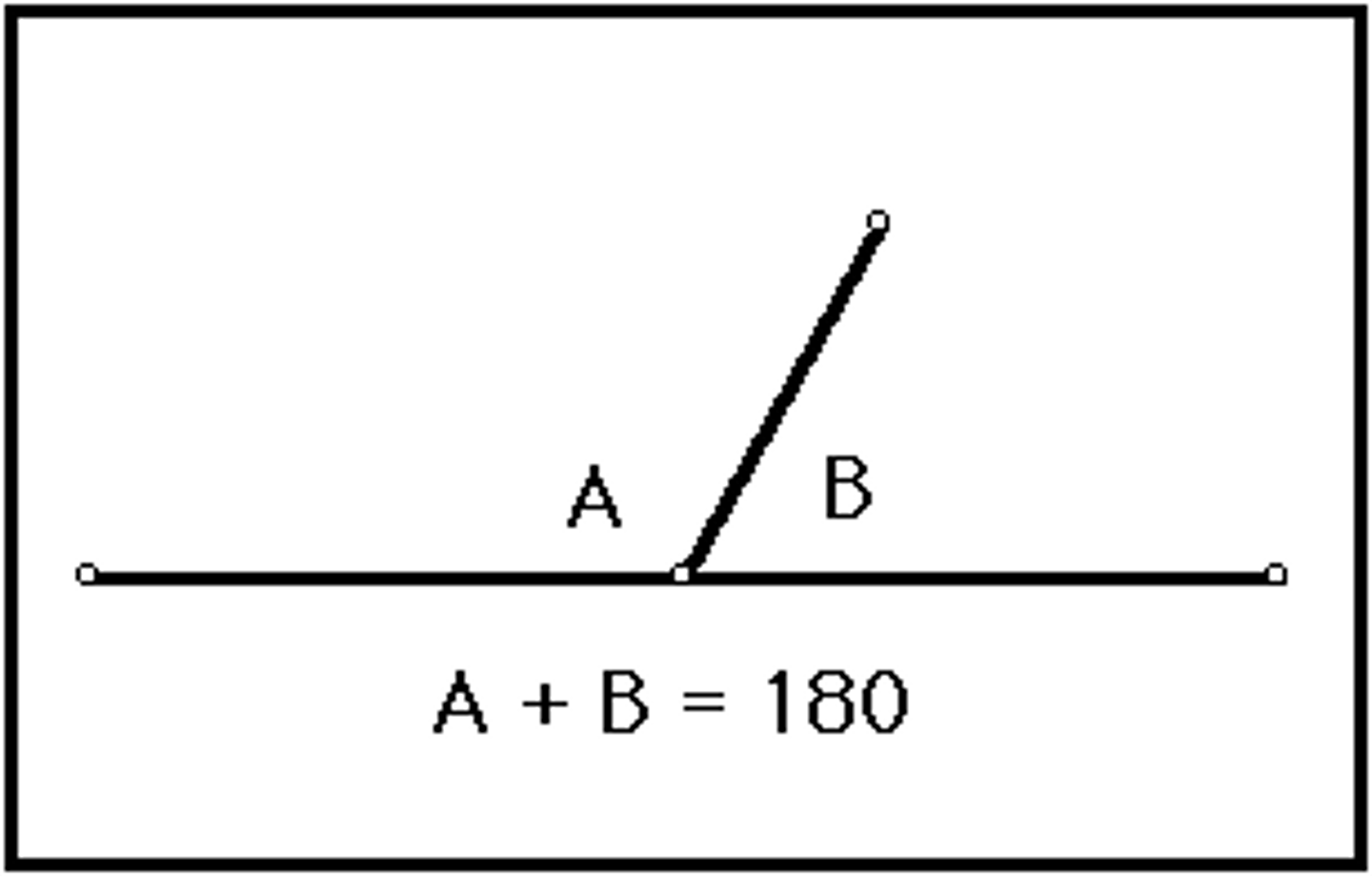
Orthogonal Pair (of Angles)

adjacent angles that form right angles

-the sum is 90

-complementary

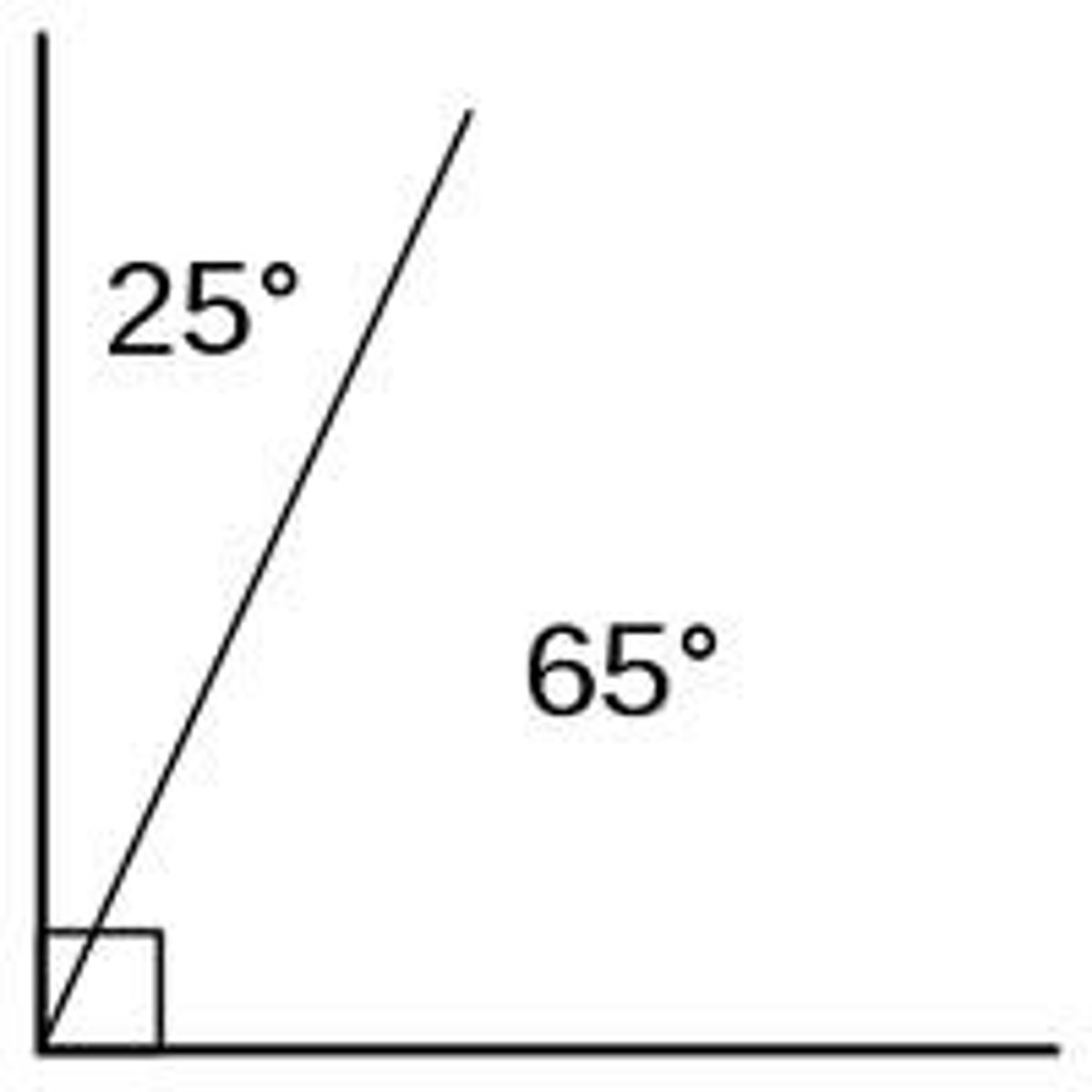
perpendicular lines

Lines that intersect to form right angles

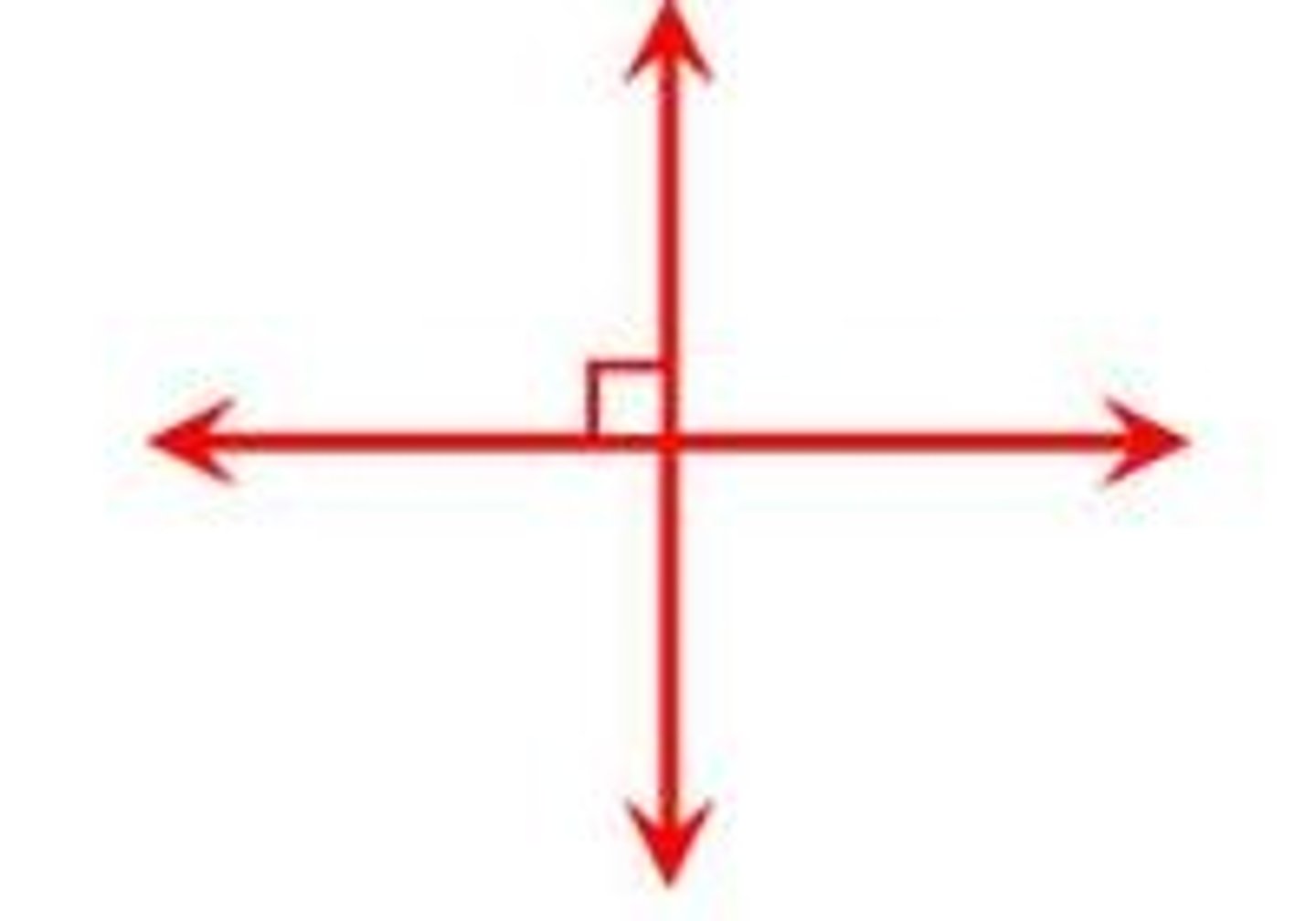
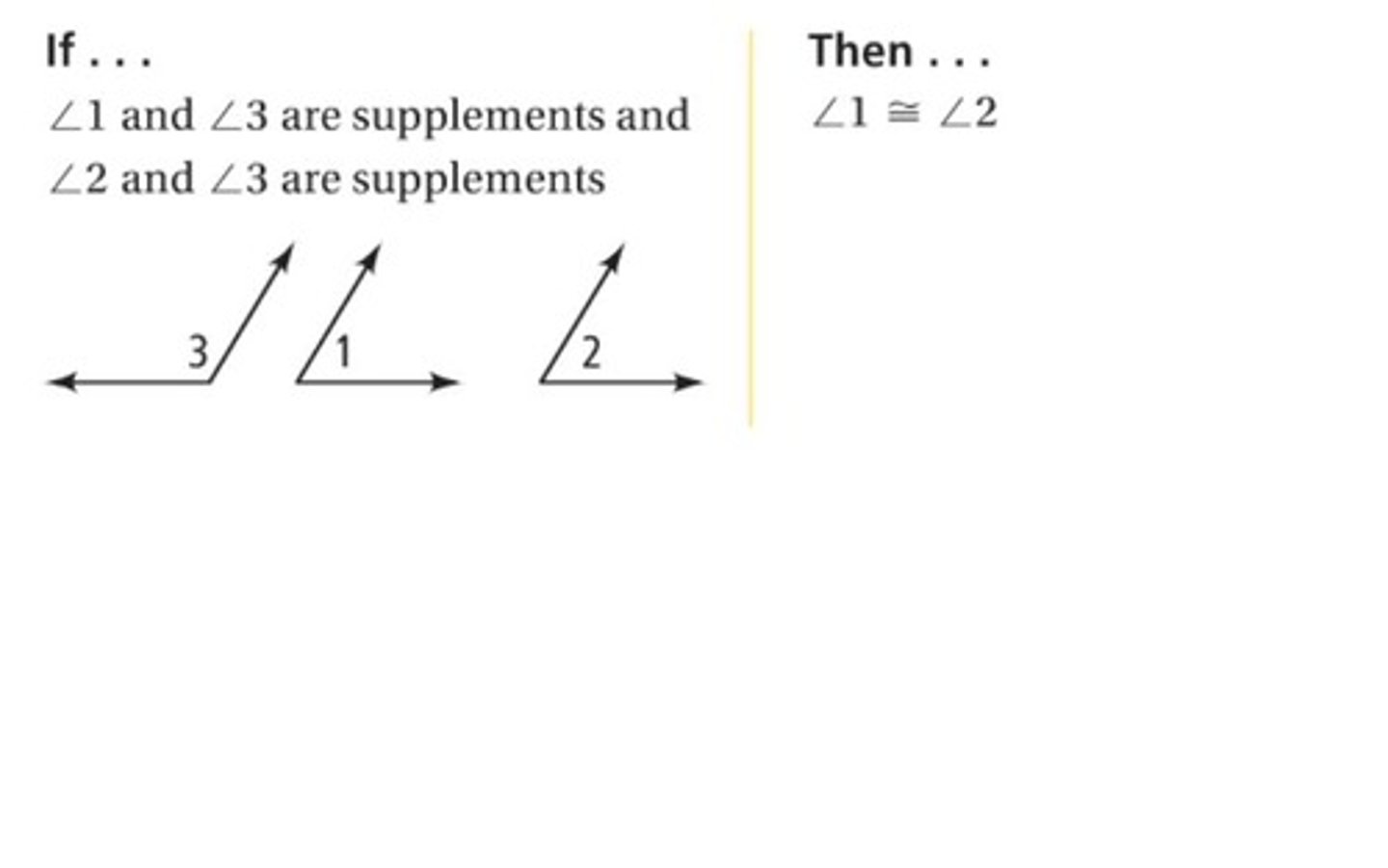
if two angles are supplements of the same angle, then...

two angles are congruent (same angle)

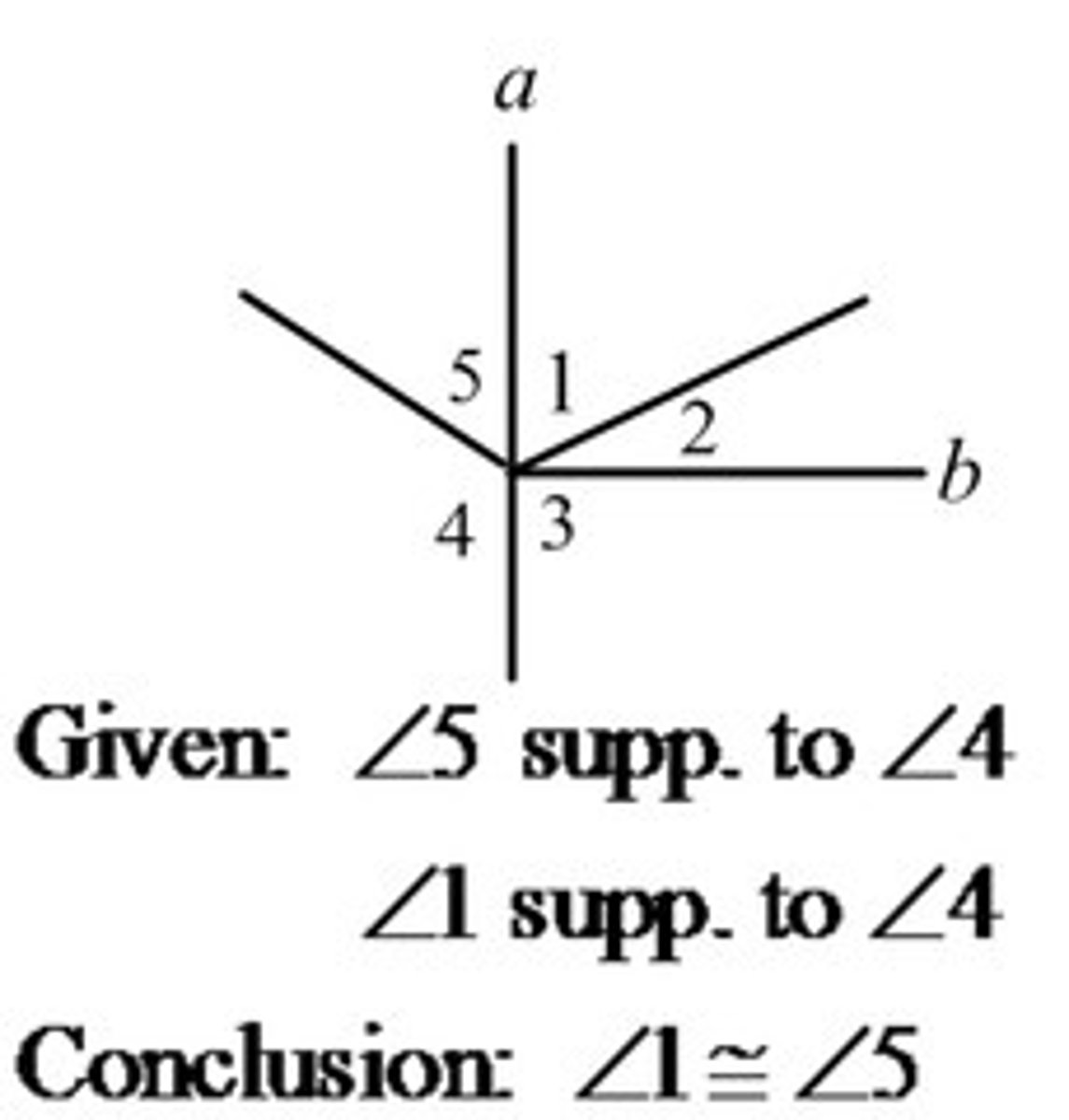
Vertical angles are..

congruent

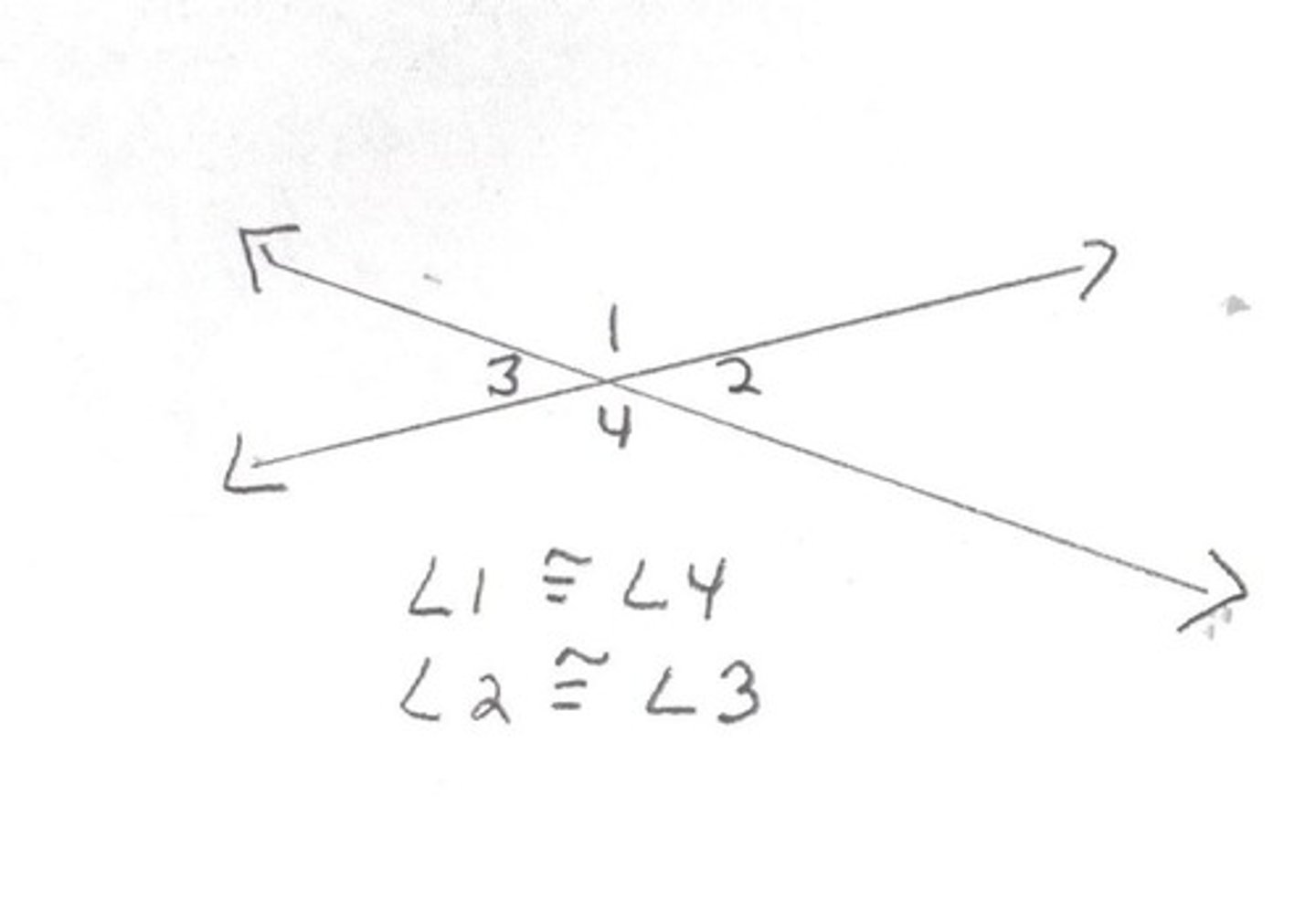
If two angles are supplements of the congruent angles,

the two angles are congruent (congruent angles)

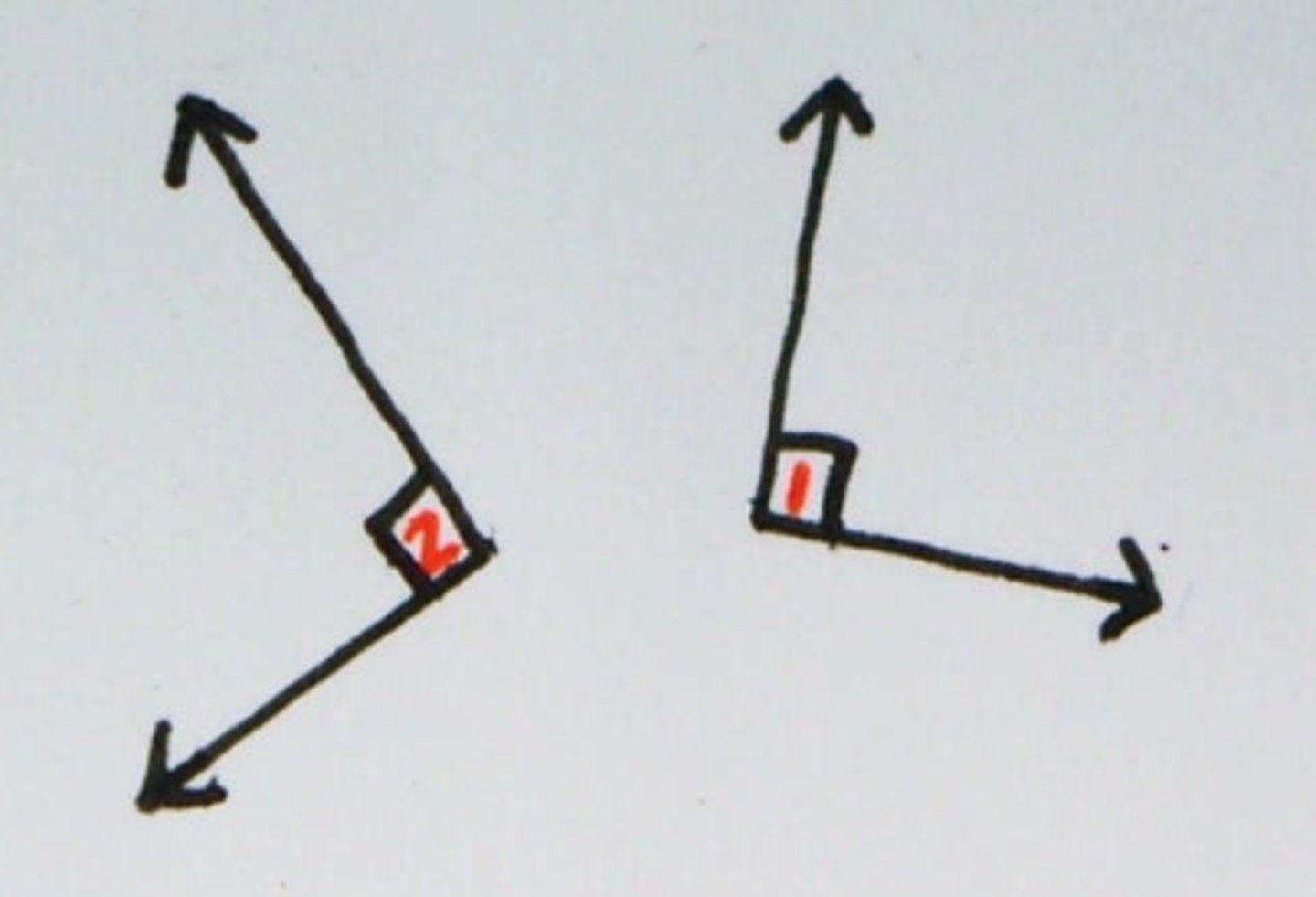
Right Angle Congruence Theorem

All right angles are congruent

(must write def)

If two lines are perpendicular, they form ______ ______ angles

congruent adjacent

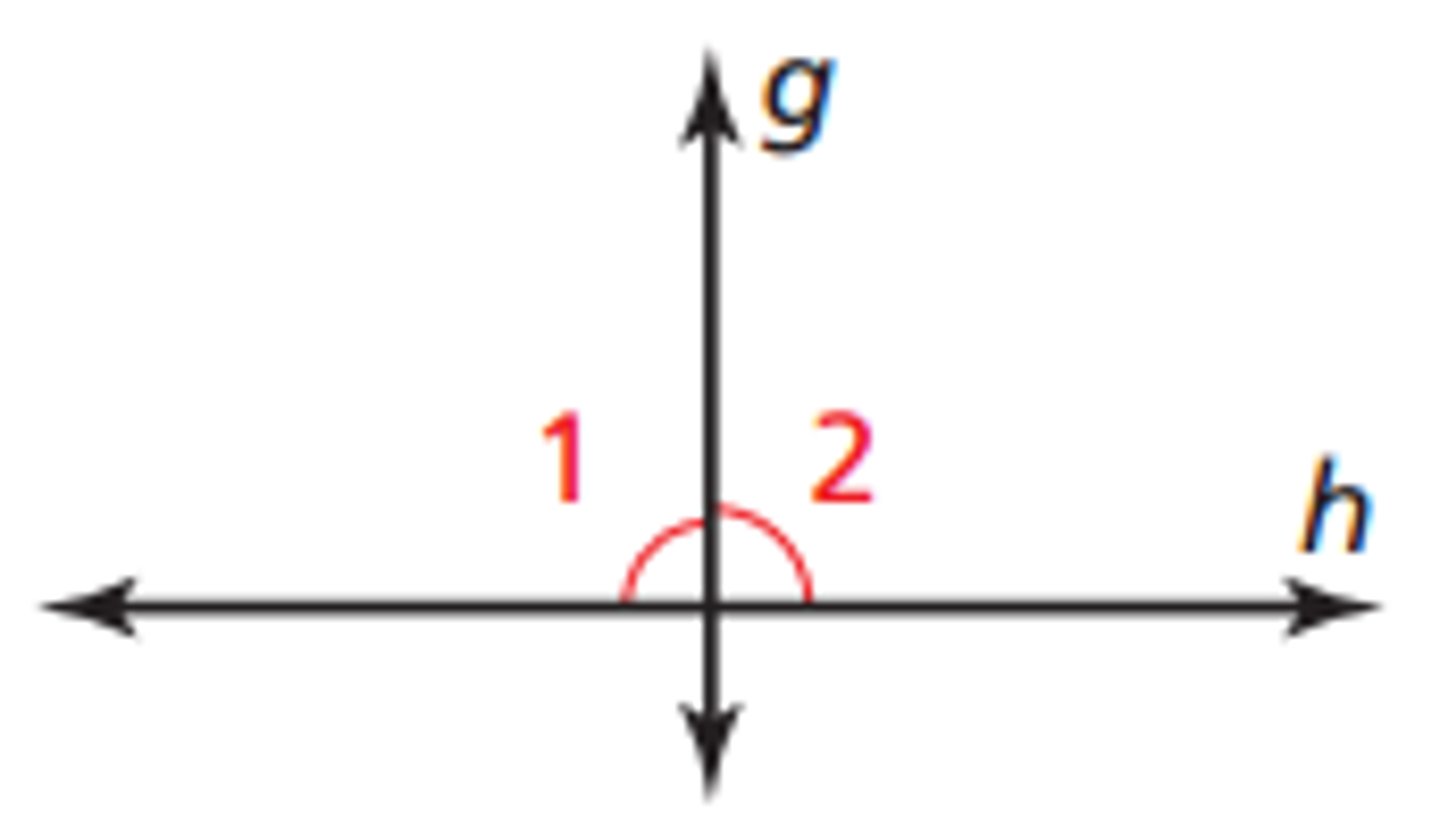
If two lines form congruent adjacent angles, then the lines are....

perpendicular

if an angle is bisected, then the measure of the resulting angle is _____ as large as the original

angle is half

The midpoint of a line segment divides that segment into two segments that are each ---- as large as the original segment.

each half as large

parallel lines

Coplanar lines that do not intersect.

- Their slopes are equal.

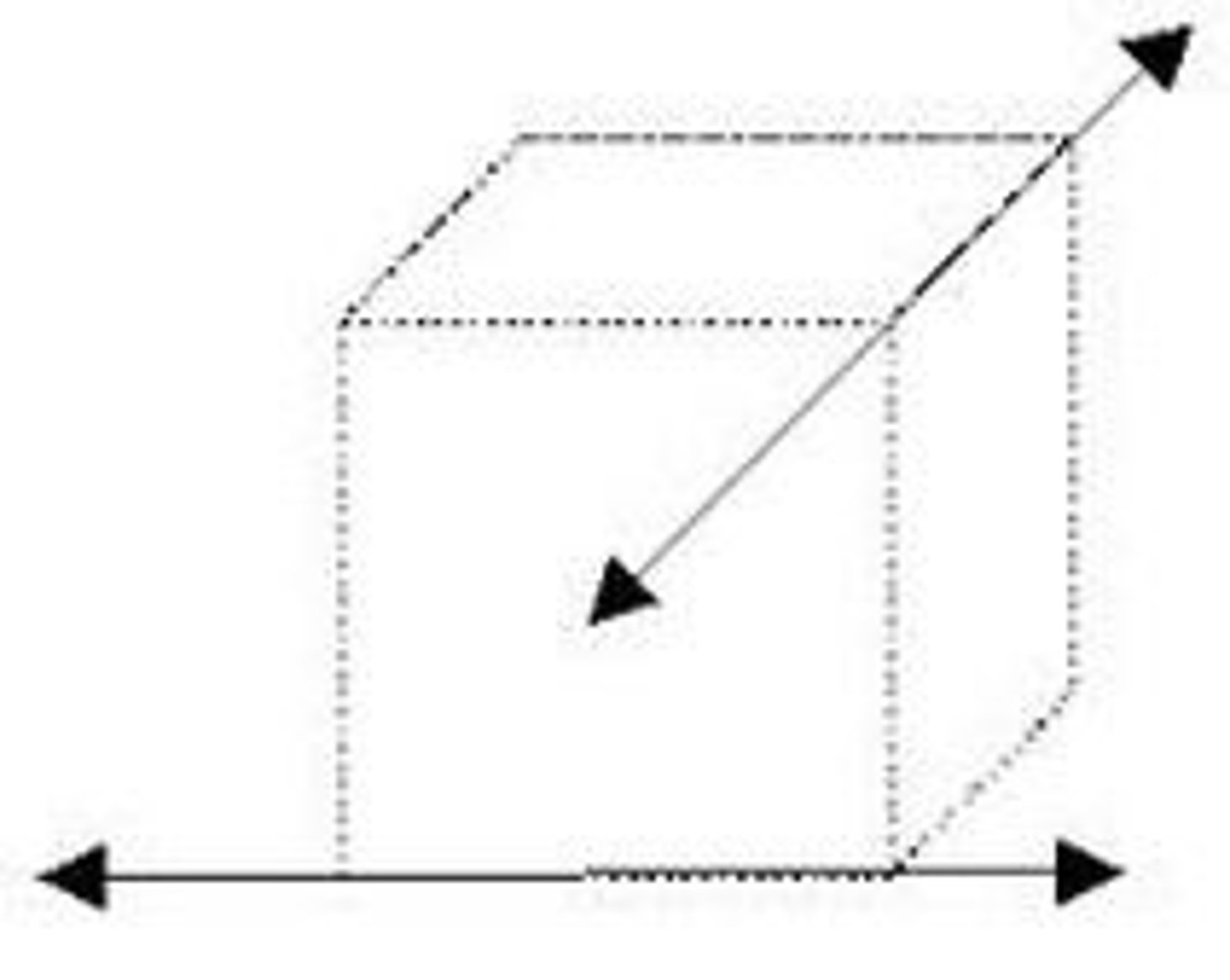
skew lines

Lines that do not intersect and are not coplanar

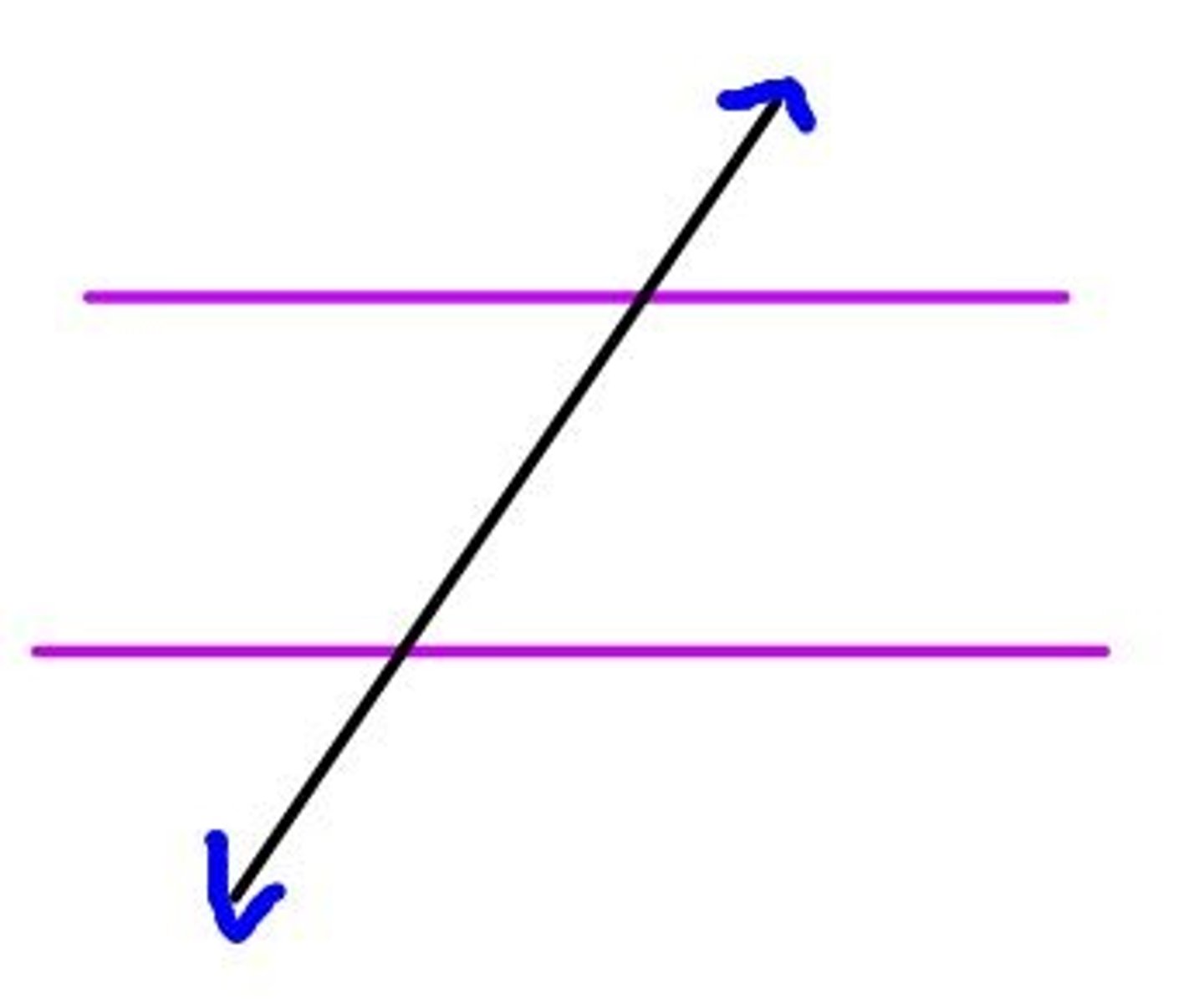
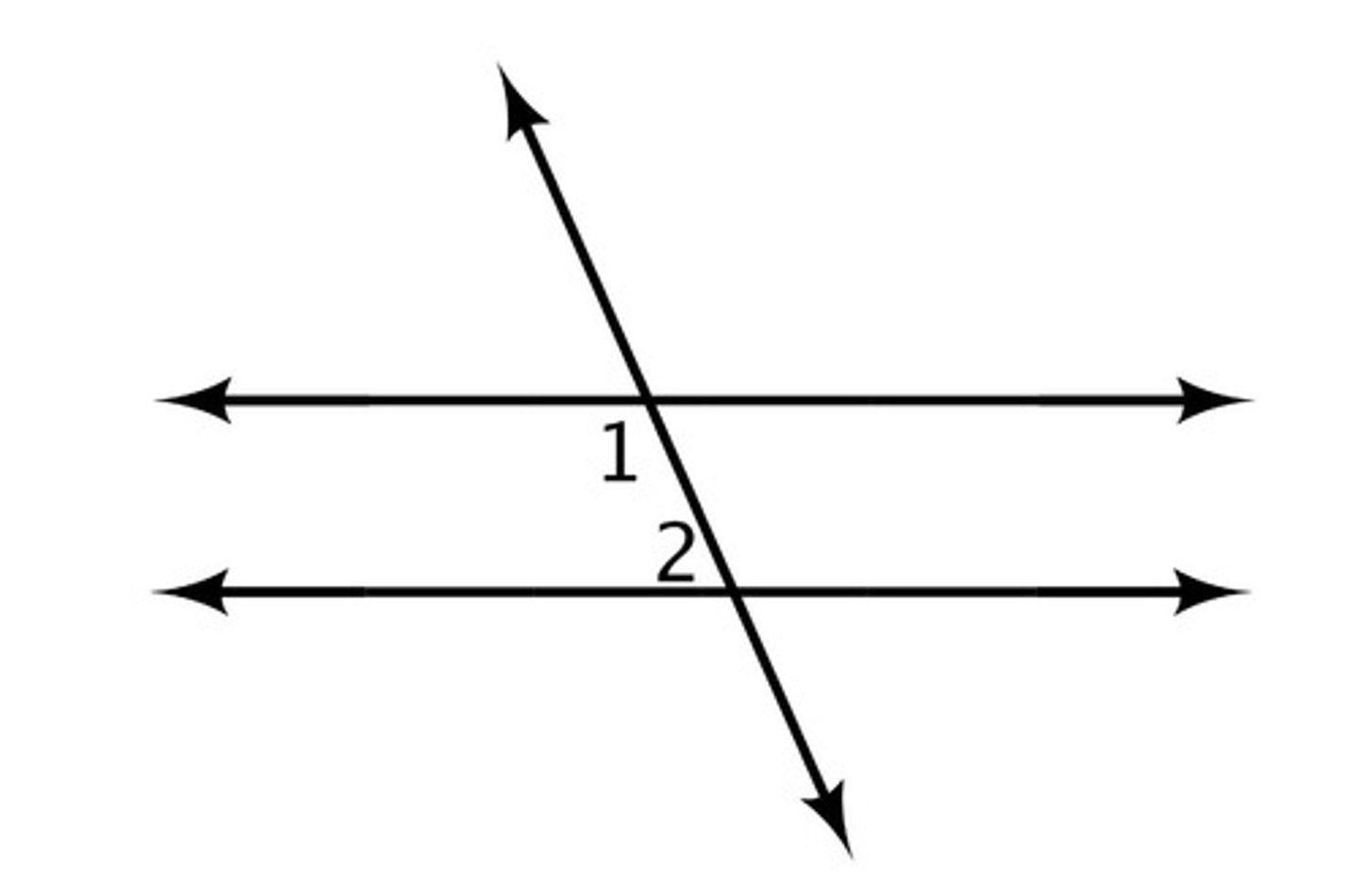
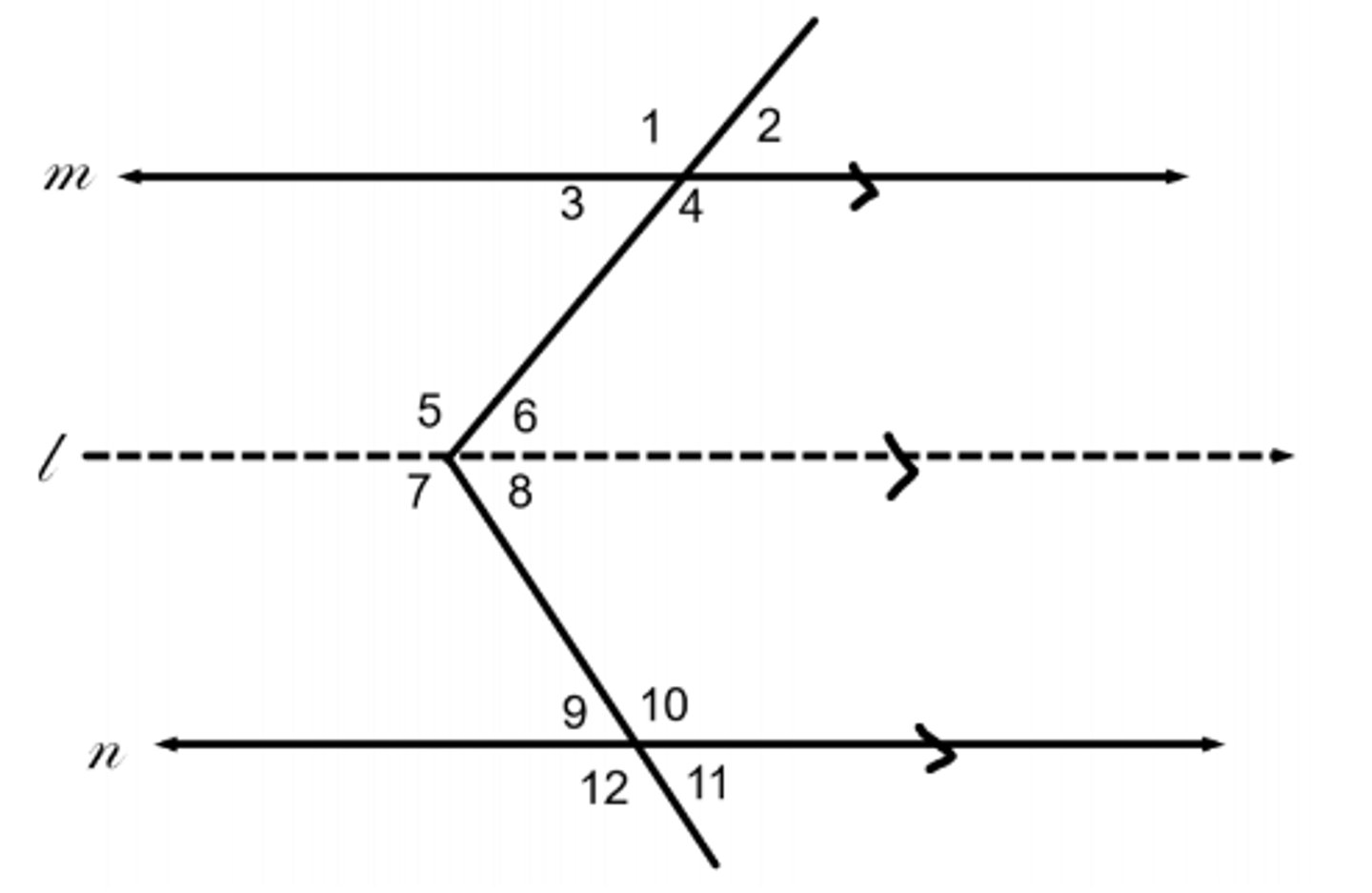
transversal

a line that intersects two or more coplanar lines at different points

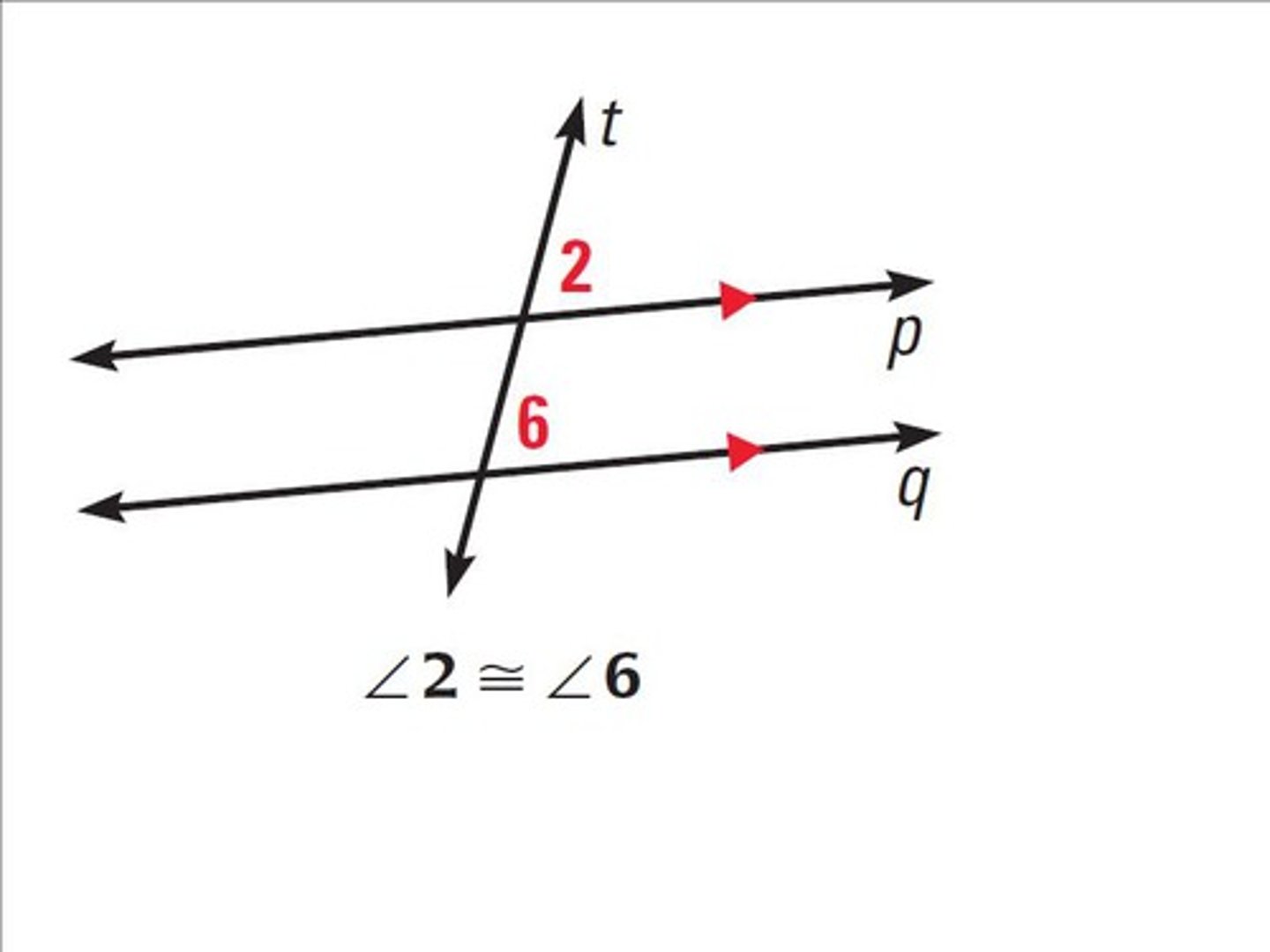
corresponding angles

lie on the same side of the transversal and in corresponding positions

alternate interior angles

nonadjacent interior angles that lie on opposite sides of the transversal

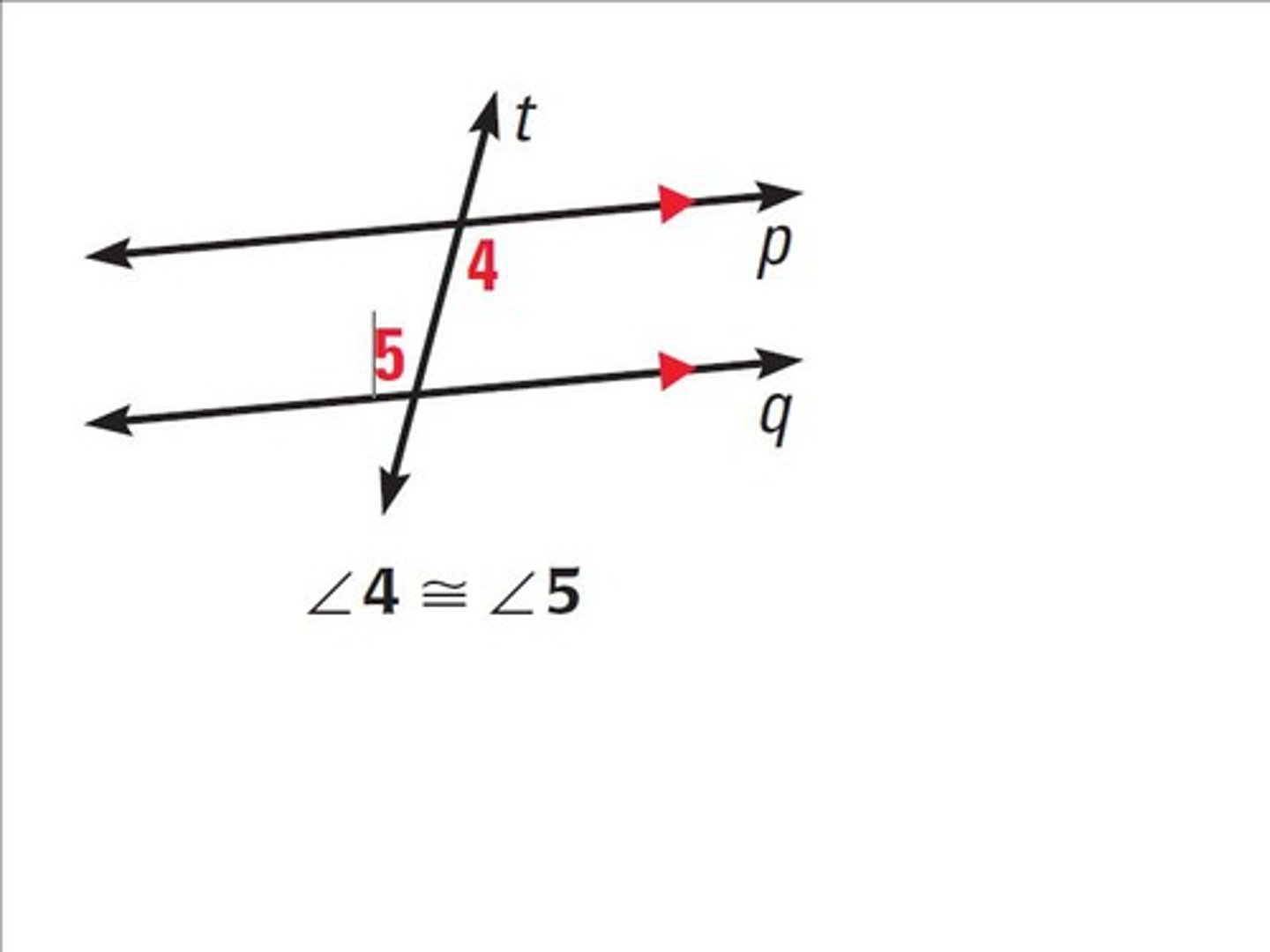
same side interior angles

two interior angles on the same side of the transversal

Corresponding angle postulate

If two parallel lines are cut by a transversal, the corresponding angles are congruent.

(works the other way around) ->

if two lines are cut by a transversal, and corresponding angles are congruent, then the two lines are paralell

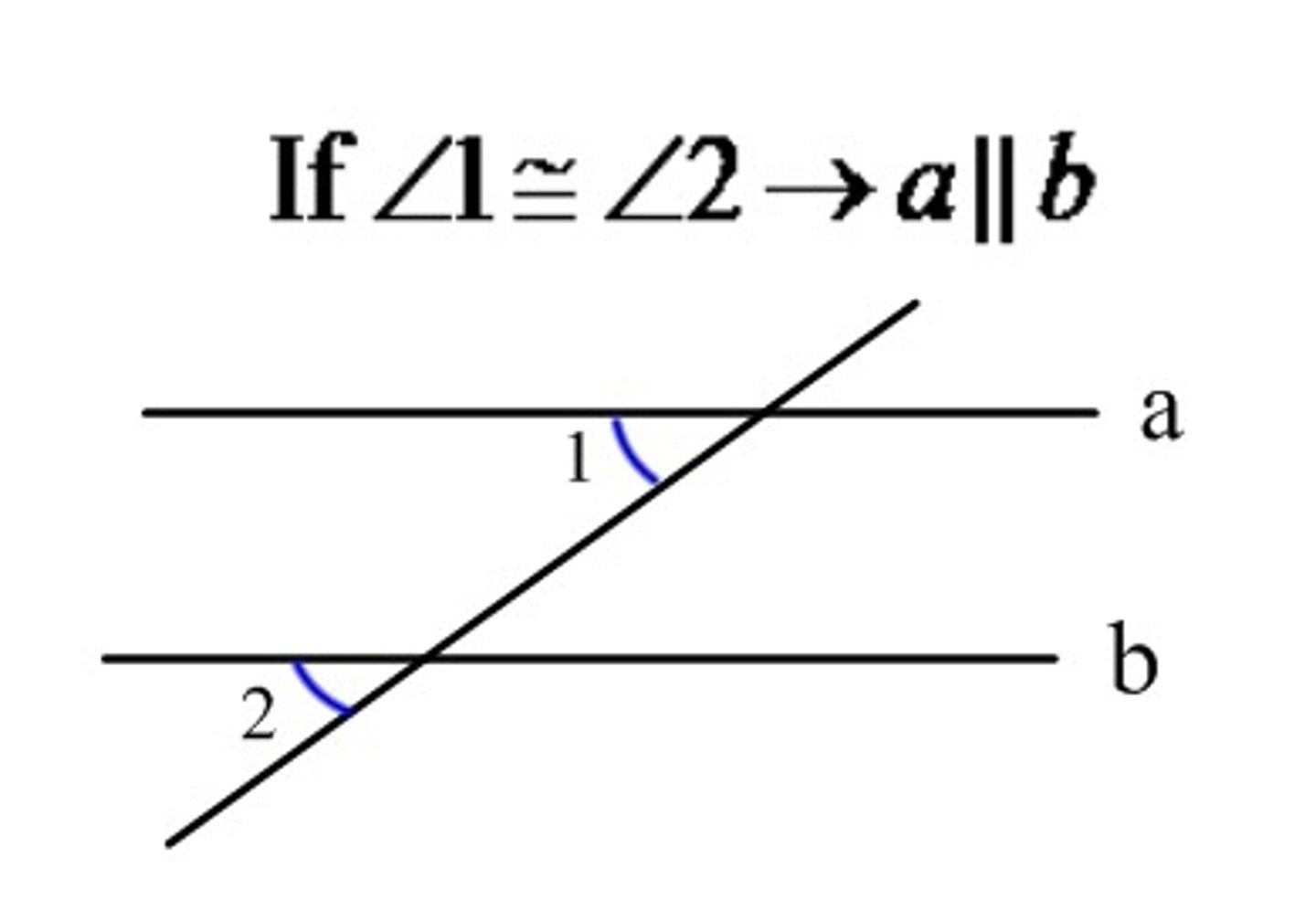
Through a point outside a line, there is ---- --- line parallel to the given line

only one

Alternate Interior Angles Theorem

If two parallel lines are cut by a transversal, then alternate interior angles are congruent.

(works the other way around) ->

if two lines are cut by a transversal and alternate interior angle are congruent, then the two lines are parallel.

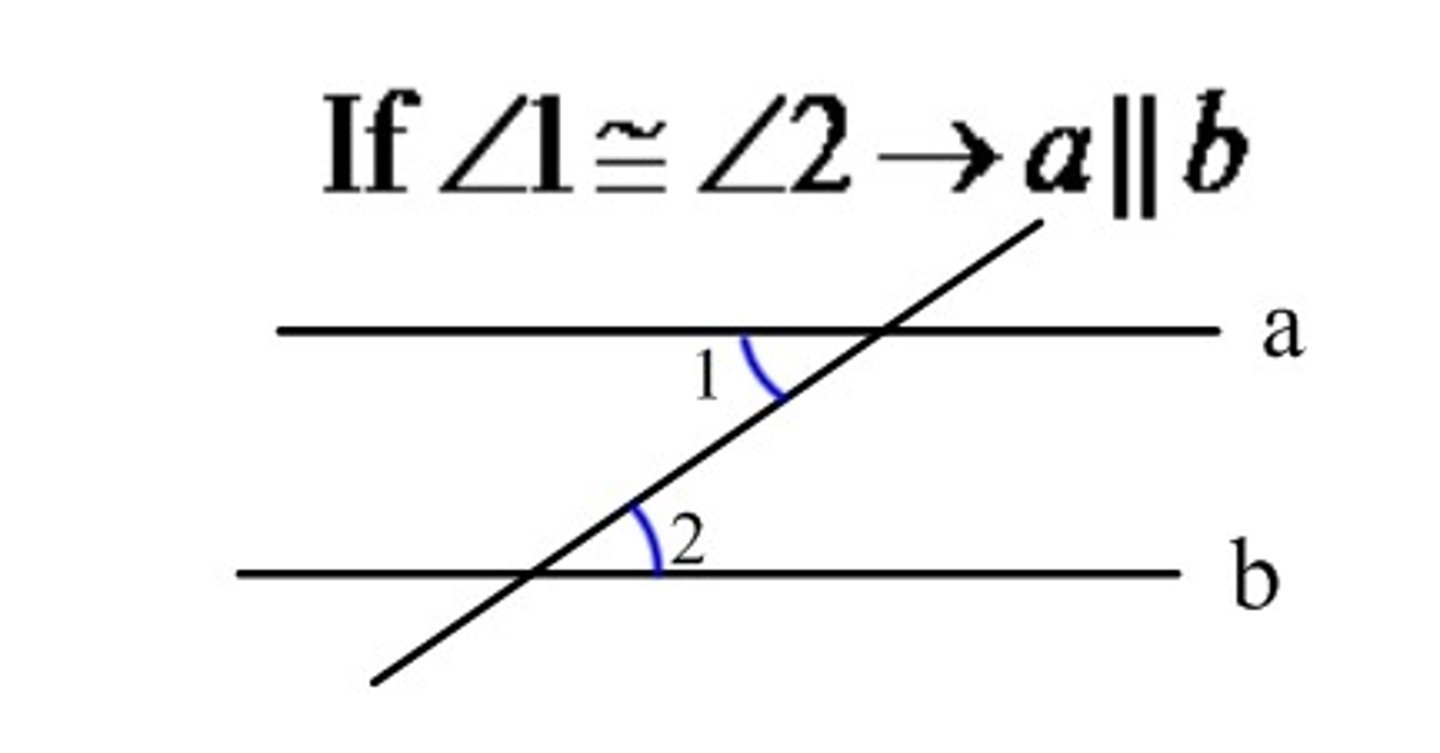
Same-Side Interior Angles Theorem

If a transversal intersects two parallel lines, then same-side interior angles are supplementary.

(works the other way around) ->

if two lines are cut by a transversal and same side interior angles are congruent, then the two lines are parallel.

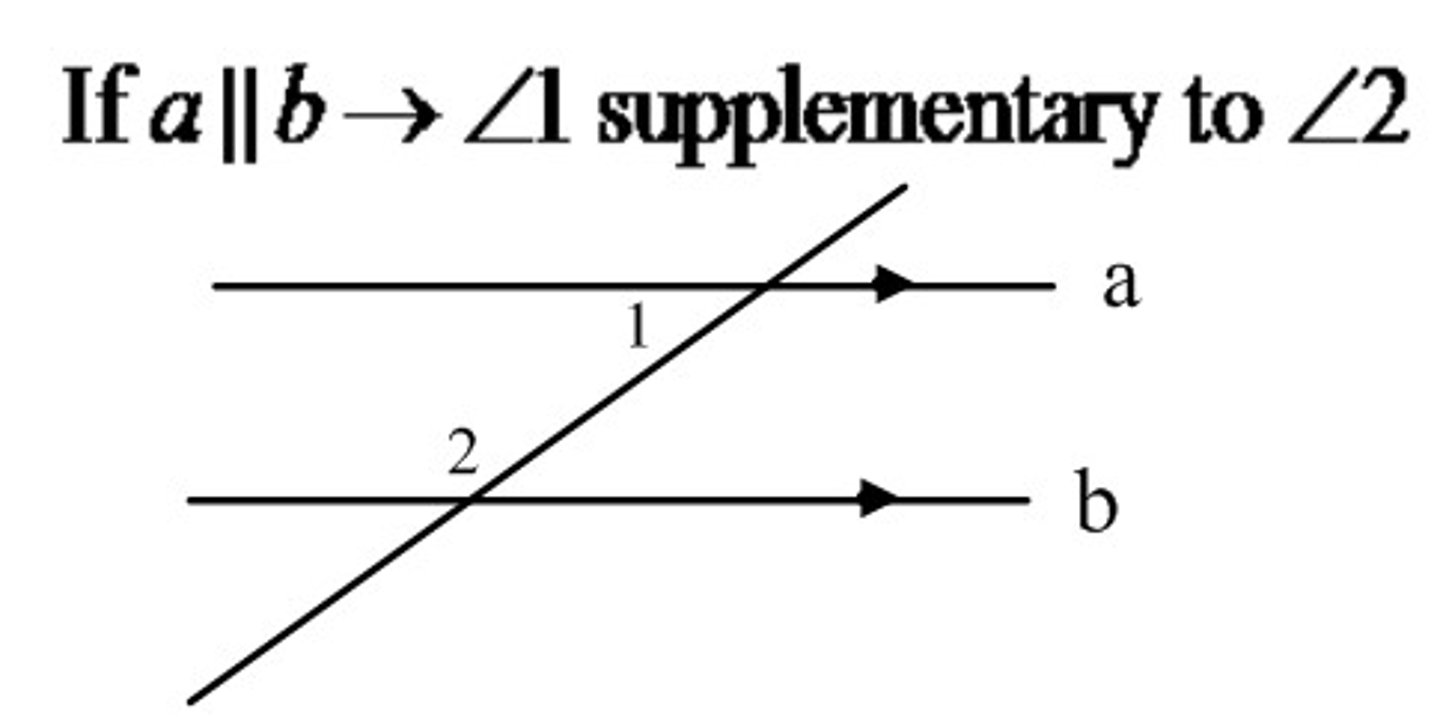
Alternate Exterior Angles Theorem

If two parallel lines are cut by a transversal, then the pairs of alternate exterior angles are congruent.

(works the other way around) ->

if two lines are cut by a transversal, and alternate exterior angles are congruent, then the two lines are parallel.

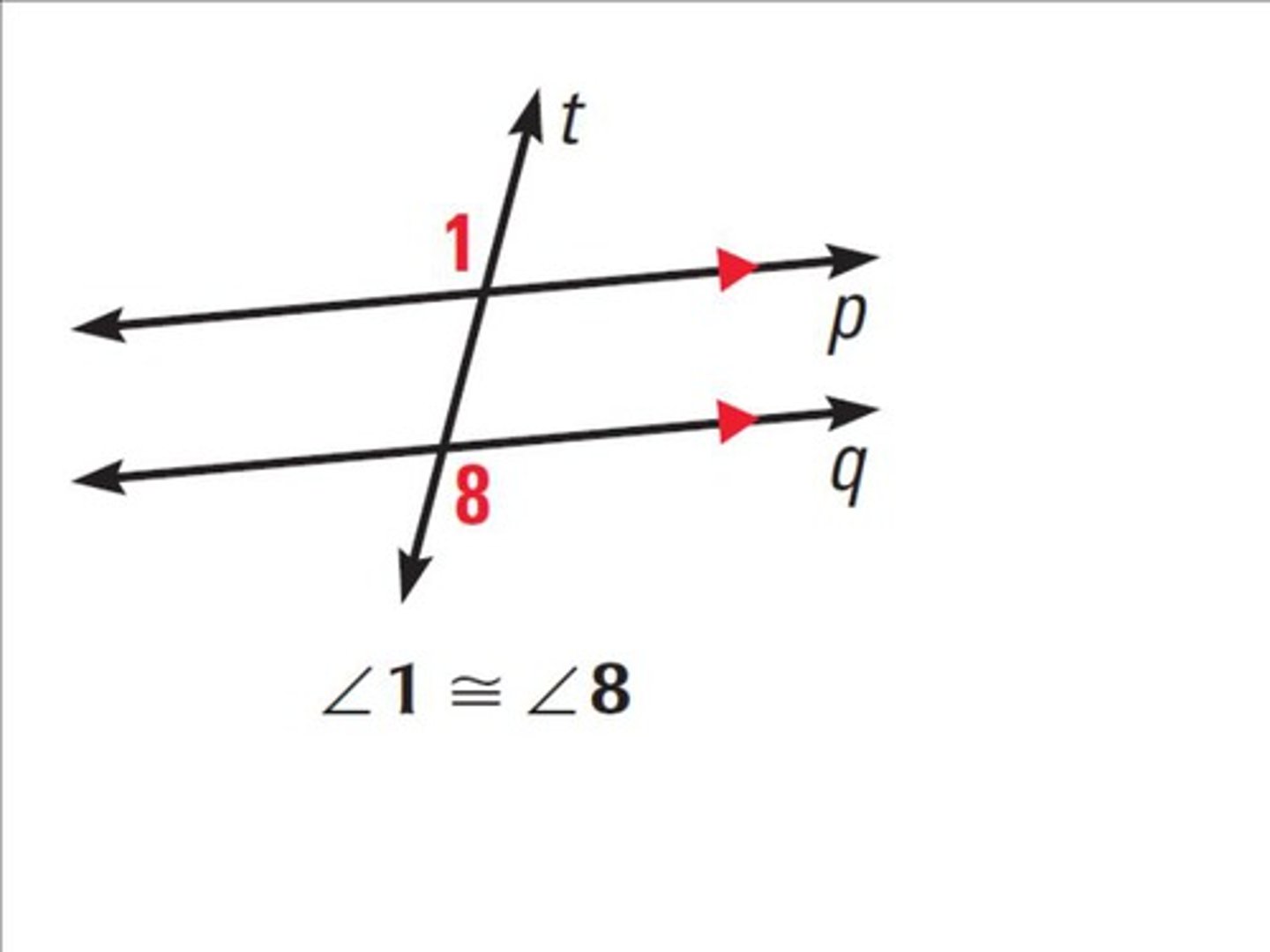
Perpendicular Transversal Theorem

If a transversal is perpendicular to one of two parallel lines, then it is perpendicular to the other.

(works the other way) ->

if two lines are perpendicular to the same line, then the two lines are parallel.

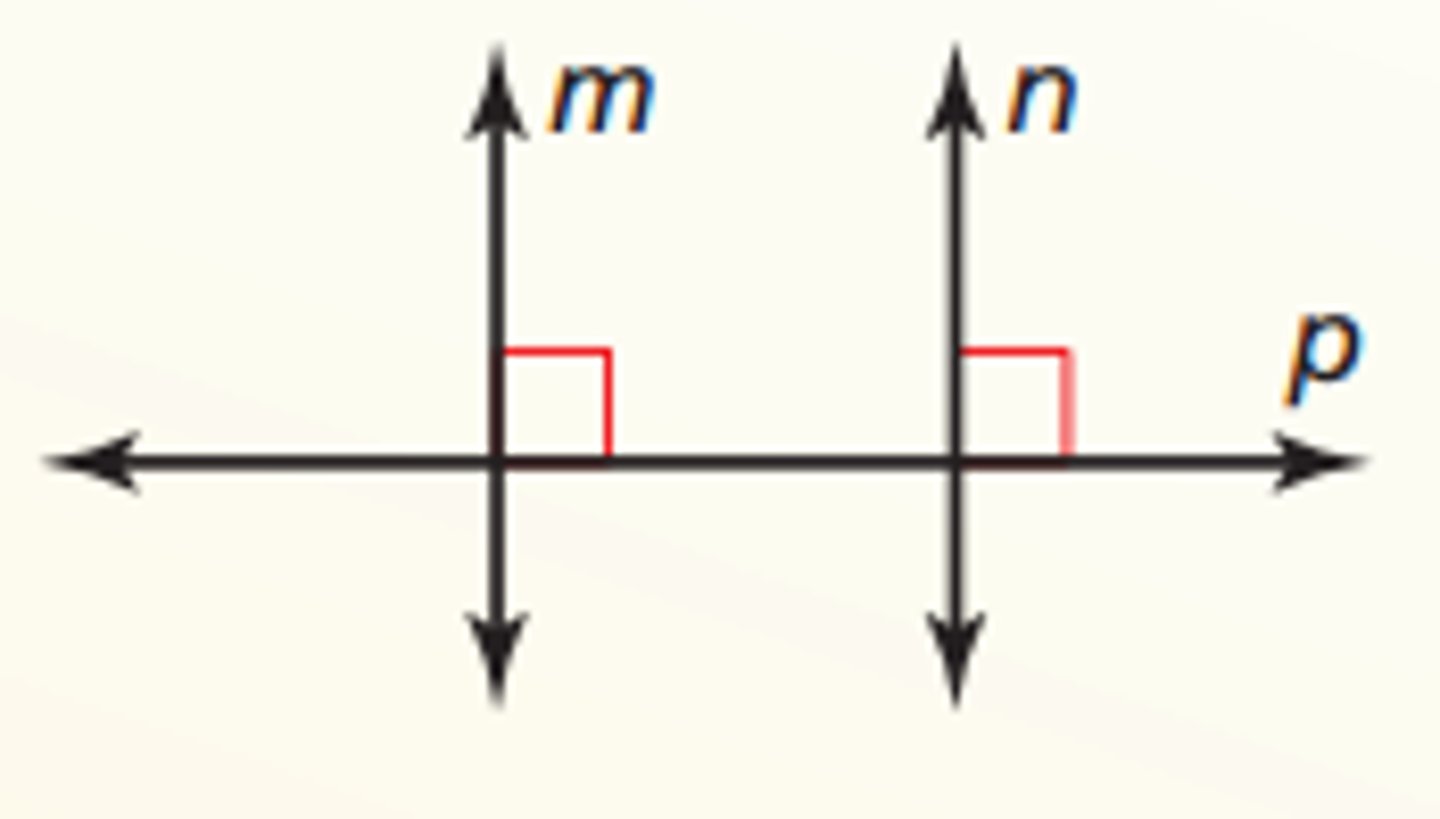
parallel line theorem

If 2 lines are parallel to a third (same) line, then they are parallel to each other

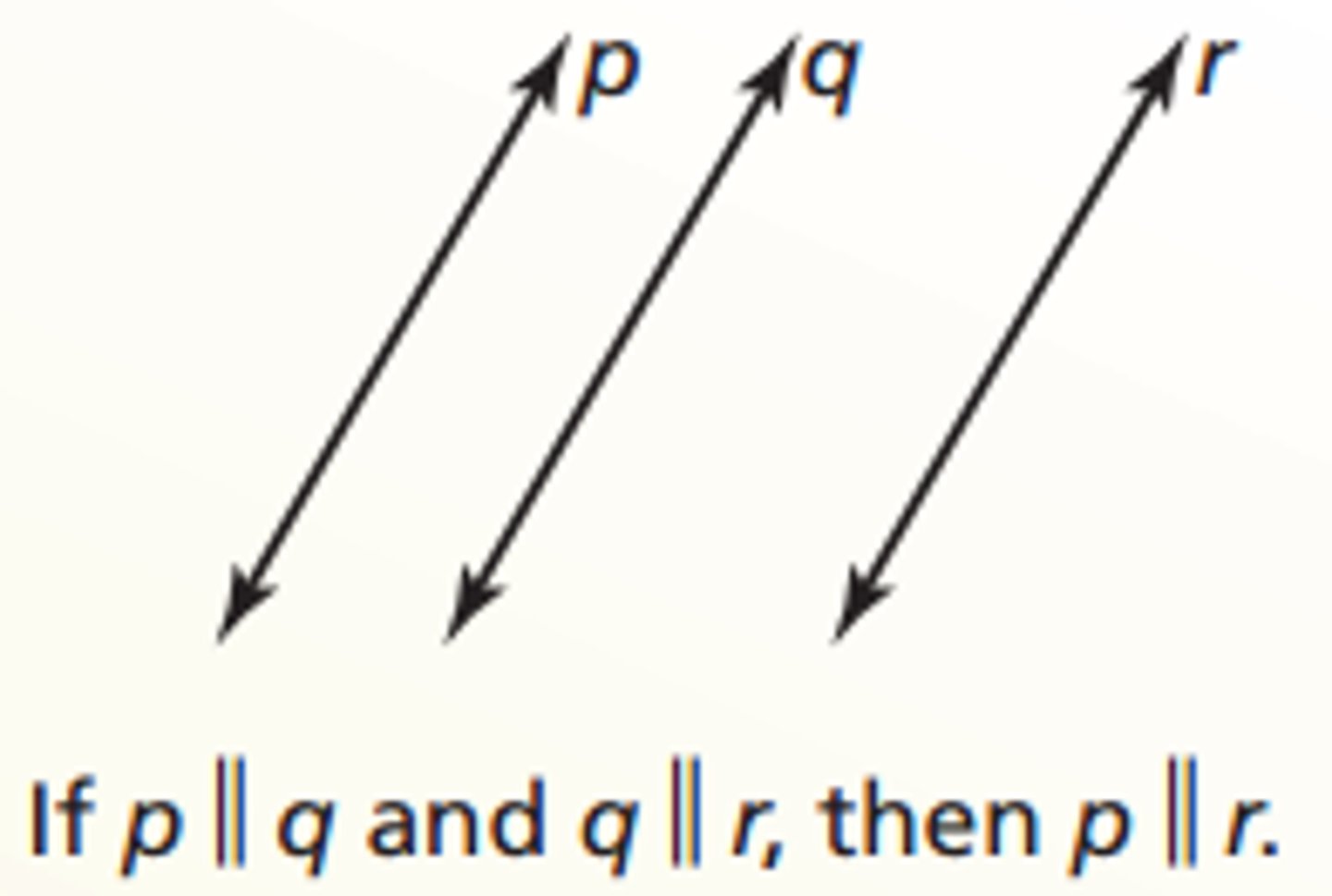
through a point outside a line there is _____ ___ line perpendicular to the first line

only one

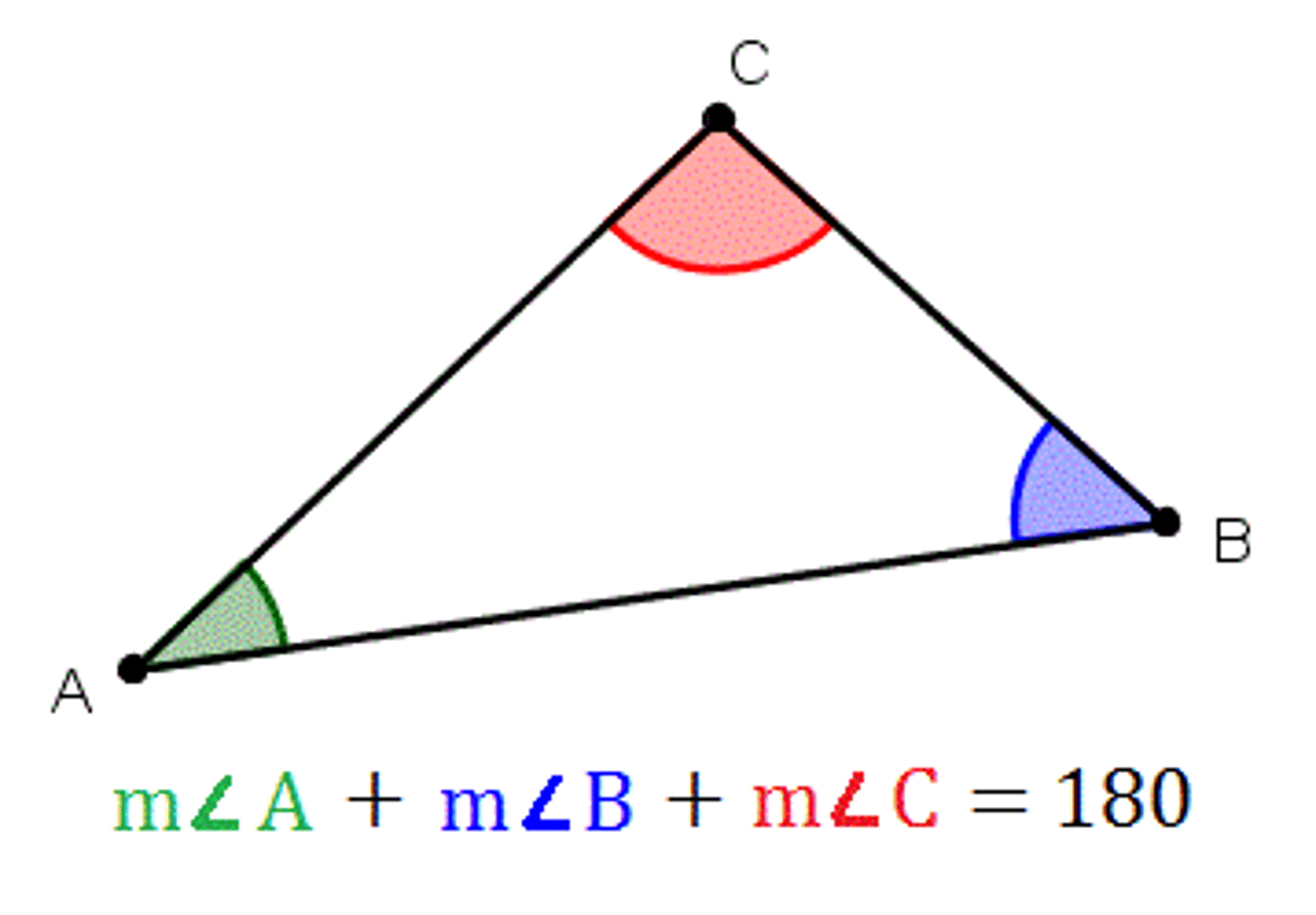
Triangle Sum Theorem

The sum of the measures of the angles of a triangle is 180.

(write out def in a proof)

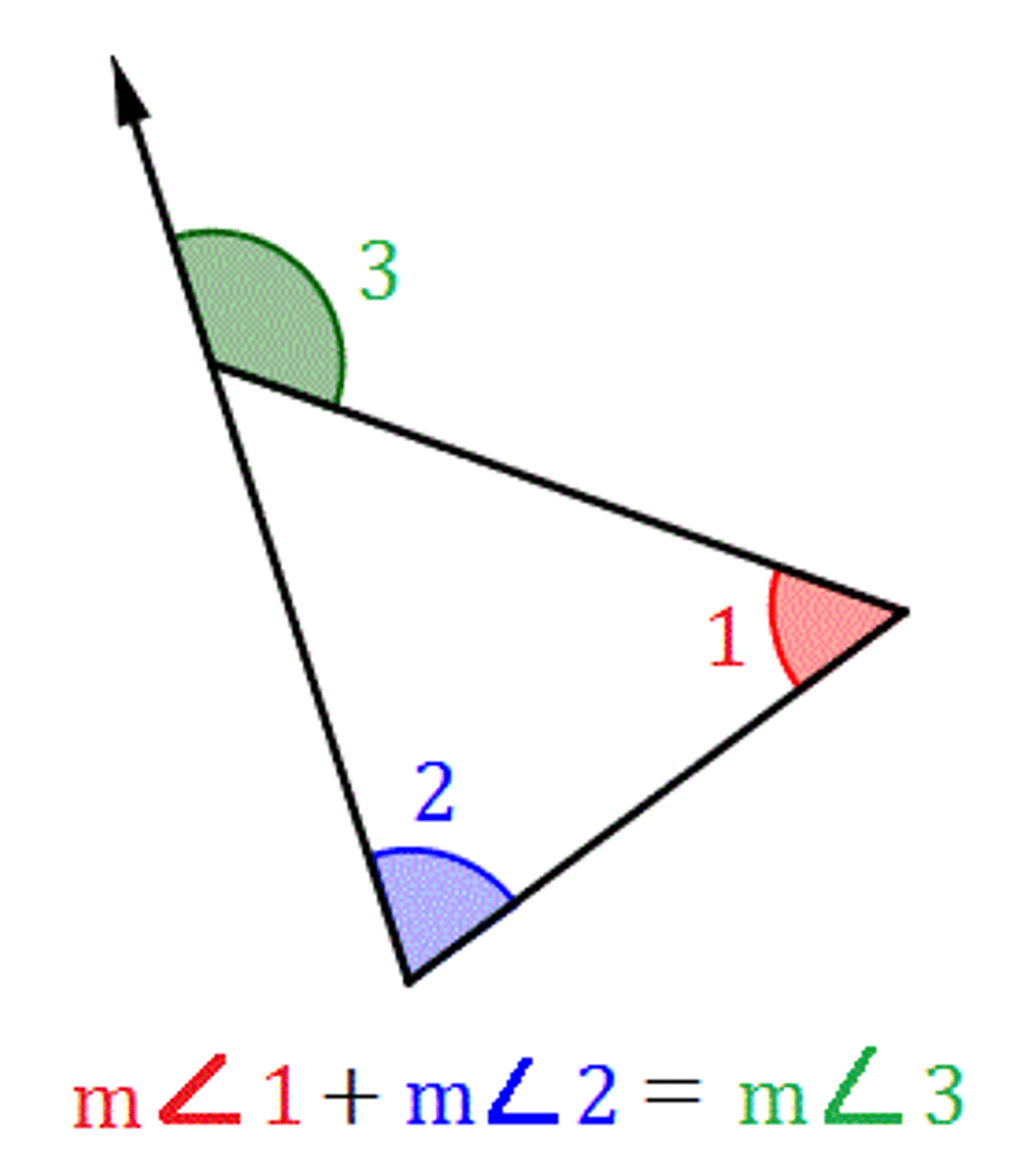
Exterior Angle Theorem

The measure of an exterior angle of a triangle is equal to the sum of the measures of the two nonadjacent(remote) interior angles.

Convex Polygon Interior Angle Sum Theorem

The sum of the interior angle measures of any convex polygon is (n-2)180

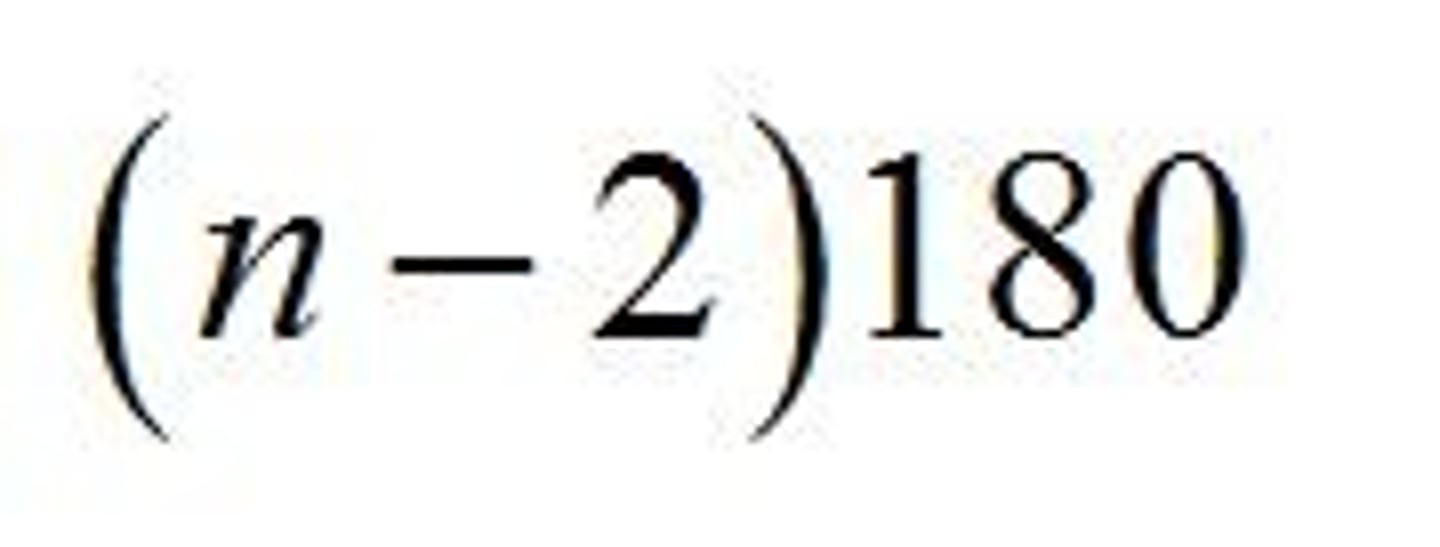
convex polygon exterior angle sum threom

the sum of the measures of the exterior angles of any convex polygon (one angle at each vertex) is 360.

corollary

a statement that can be easily proved using a theorem

Corollary #1 of Triangle Sum theorem

- angle type

in a triangle, there can be at most one right or obtuse angle.

Corollary #2 Triangle Sum Theorem

- measure of equilateral triangle angles

each angle of an equilateral/equiangular triangle has a measure of 60 degrees

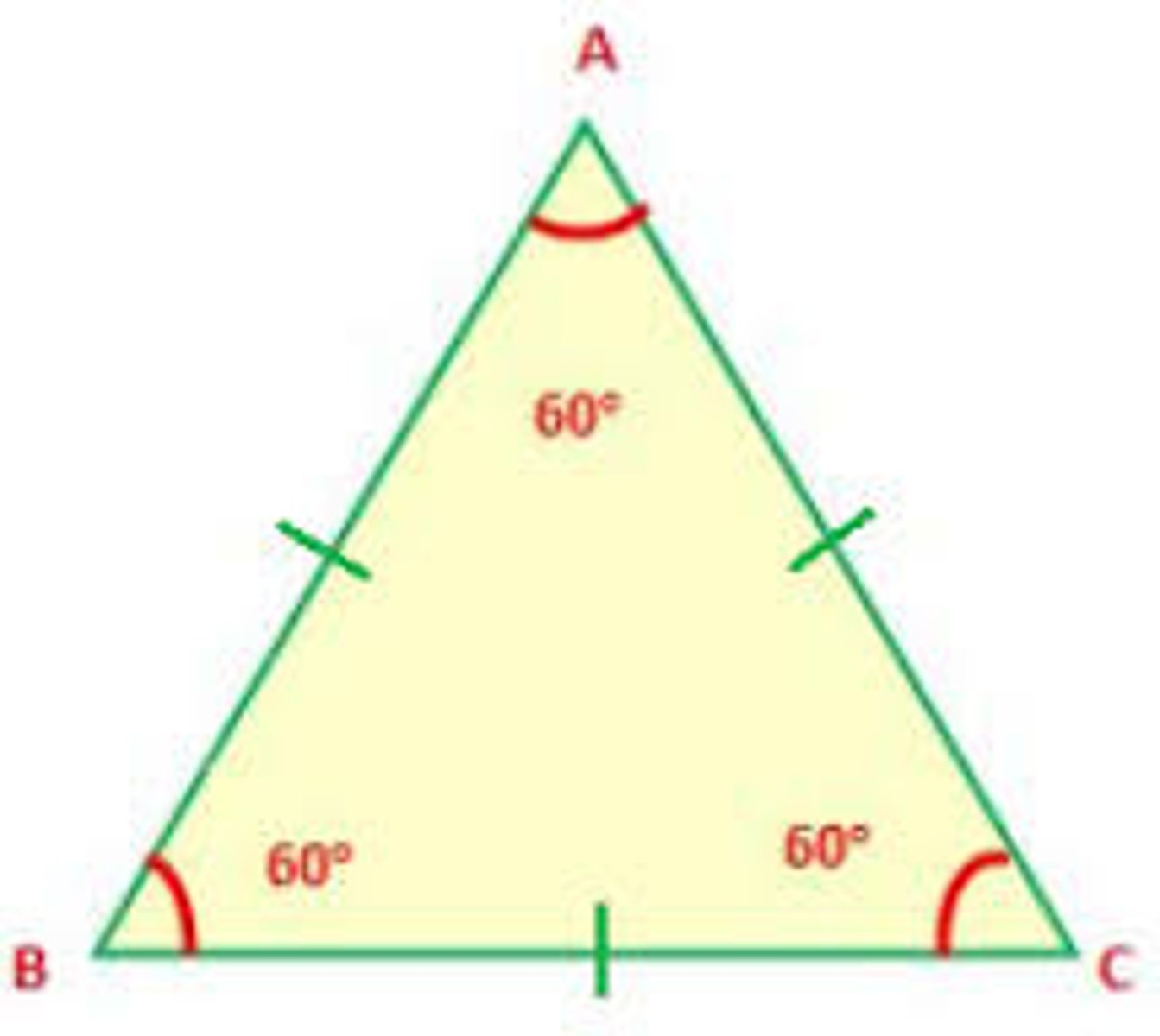
Corollary #3 of Triangle Sum Theorem

- Angles of a right triangle

The acute angles of a right triangle are complementary

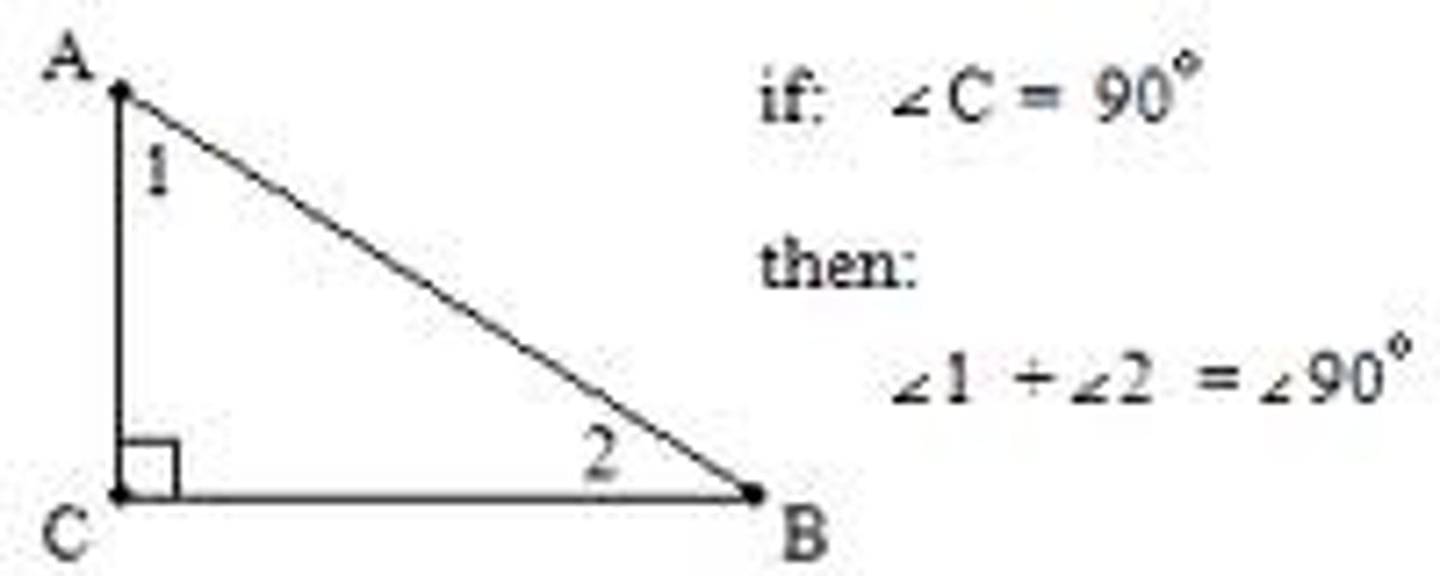
Corollary #4 of Triangle Sum Theorem

- angle congruence

if two angles of one triangle are congruent to two angles of another triangle, then the third angles are congruent.

polygon

A closed plane figure made up of coplanar line segments.

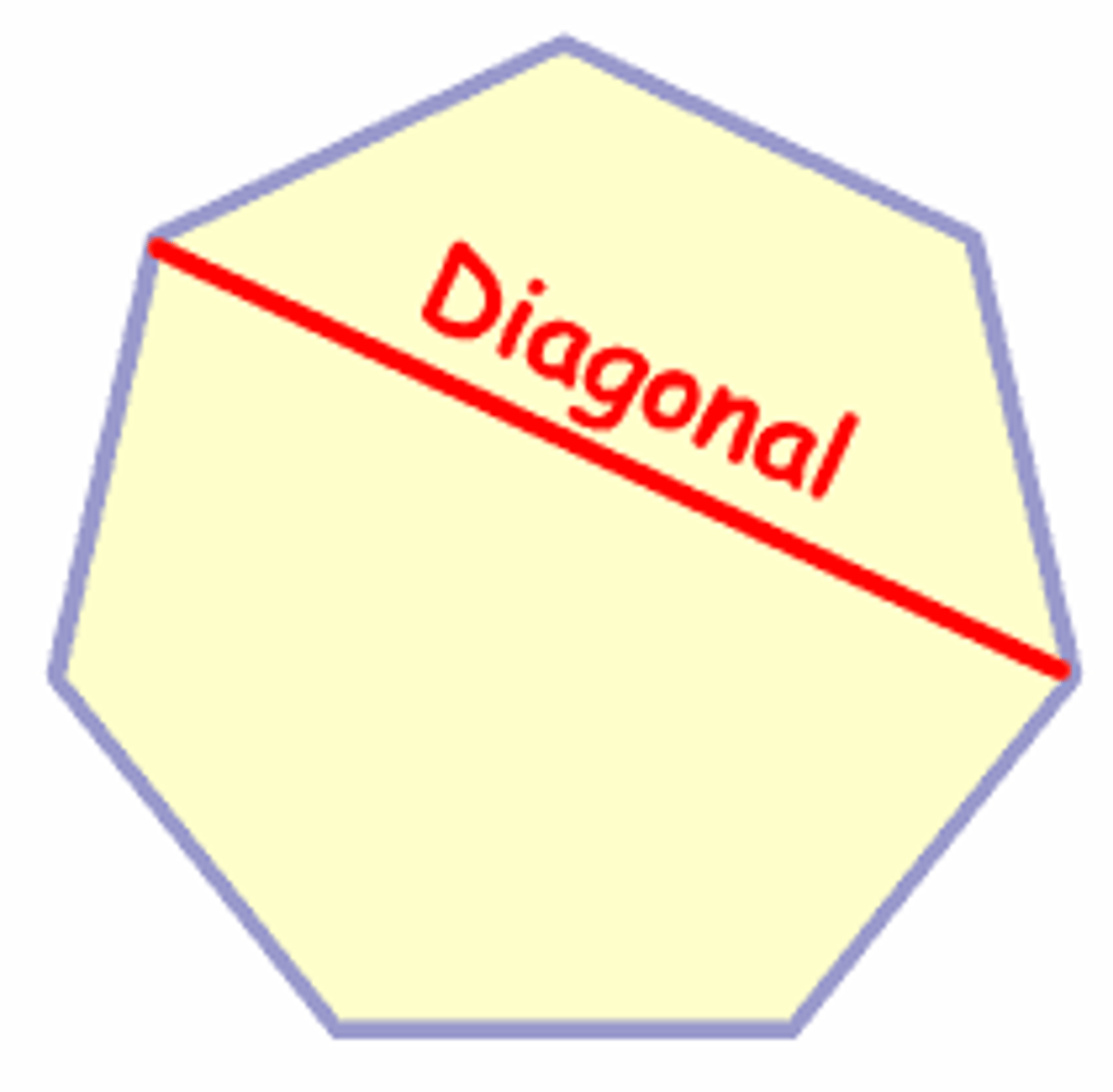
diagonal of a polygon

a segment connecting two nonconsecutive vertices of a polygon

regular polygon

a polygon that is both equilateral and equiangular

irregular polygon

a polygon with sides that are not all congruent or angles that are not all congruent

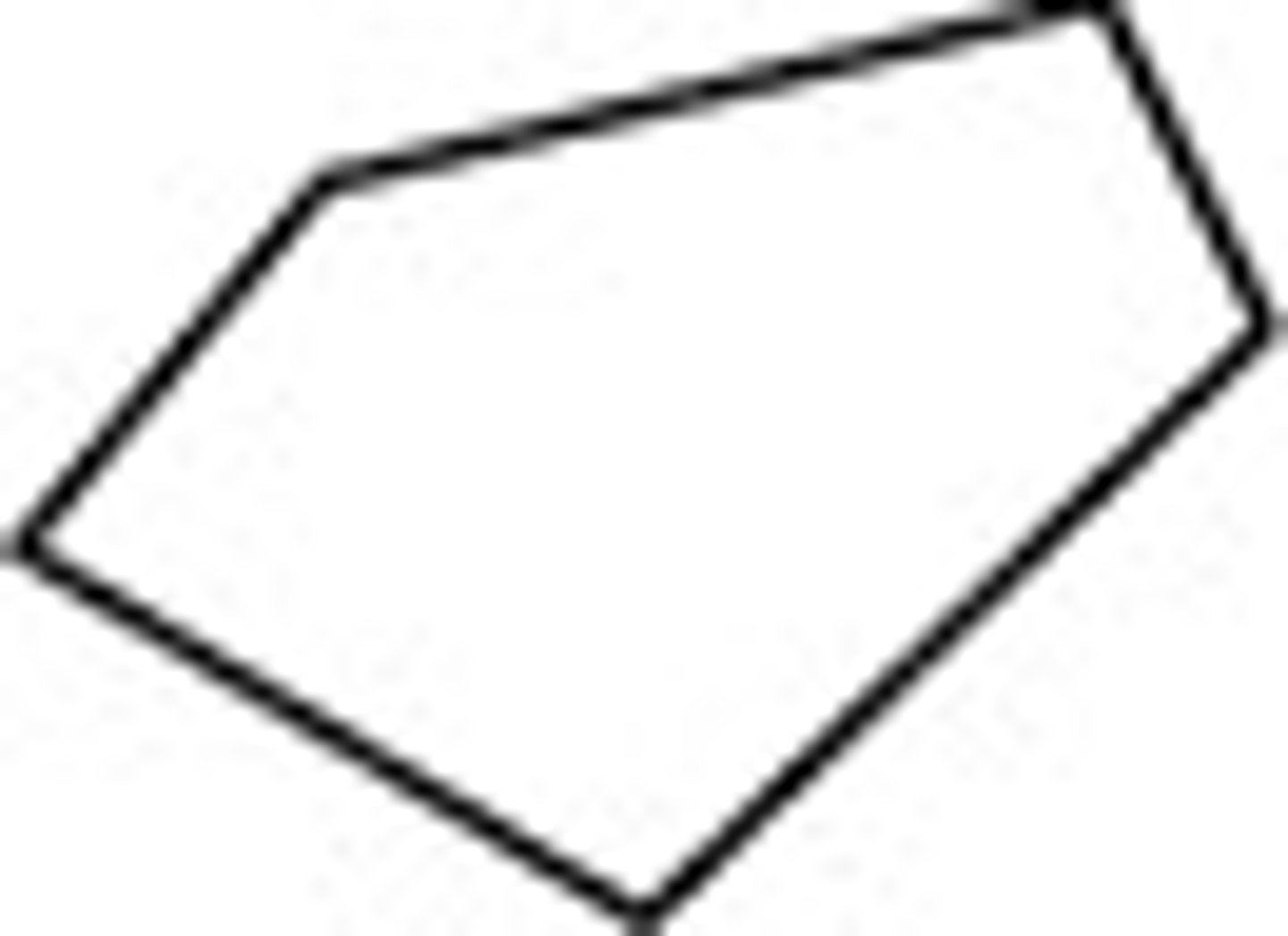
convex polygon

a polygon such that no line containing a side of the polygon contains a point in the interior of the polygon

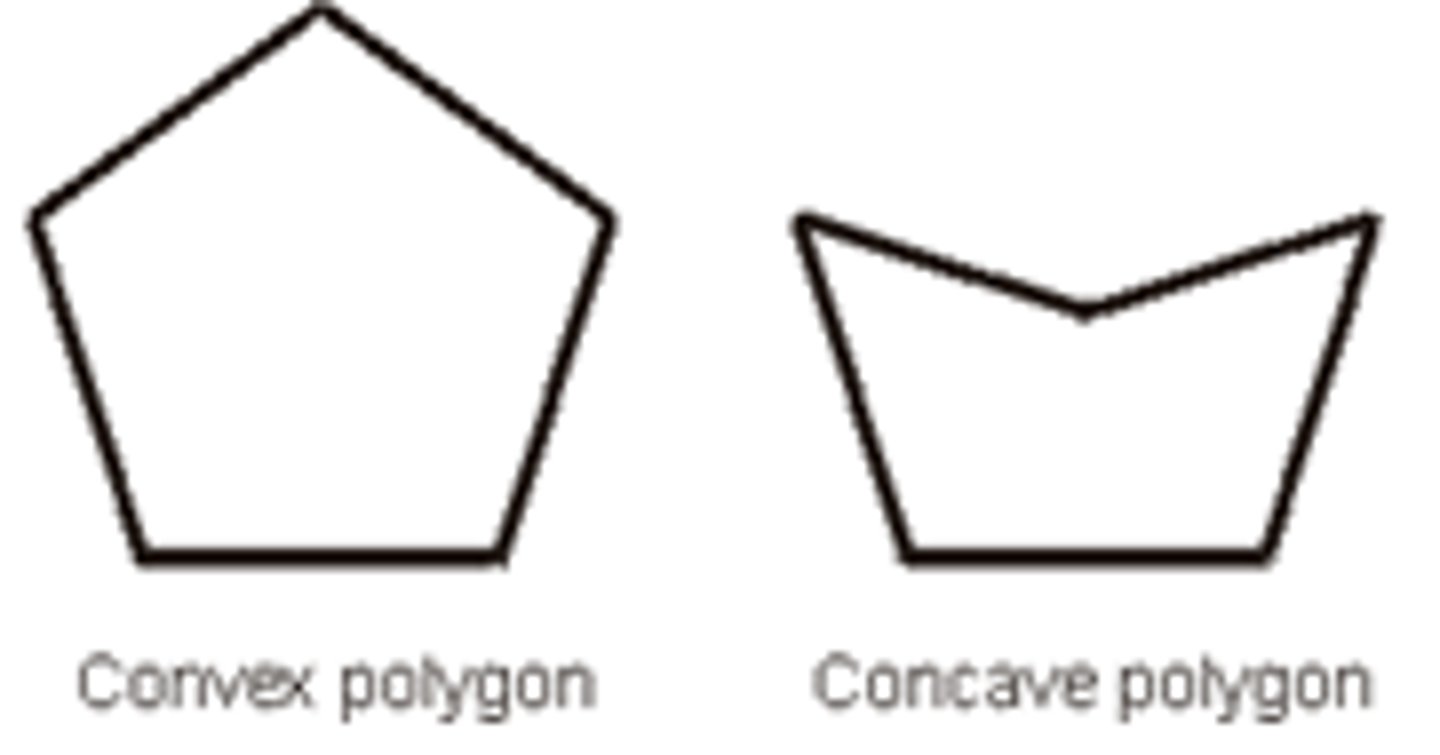
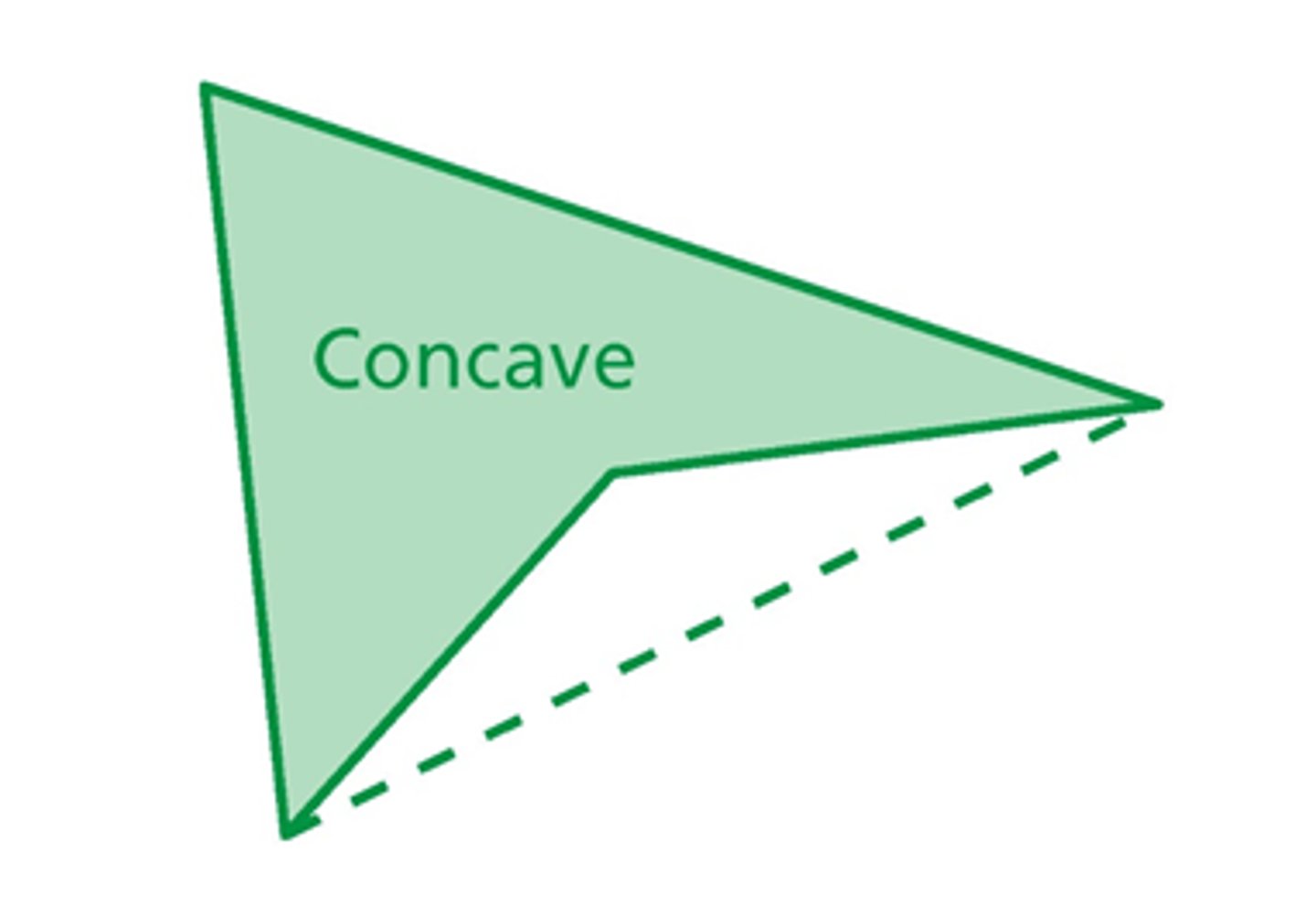
concave polygon

has at least one diagonal with points outside the polygon

formula to find sum of interior angles of a polygon

(n-2)180

formula to find the amount of diagonals in a polygon

(n-3)n/2

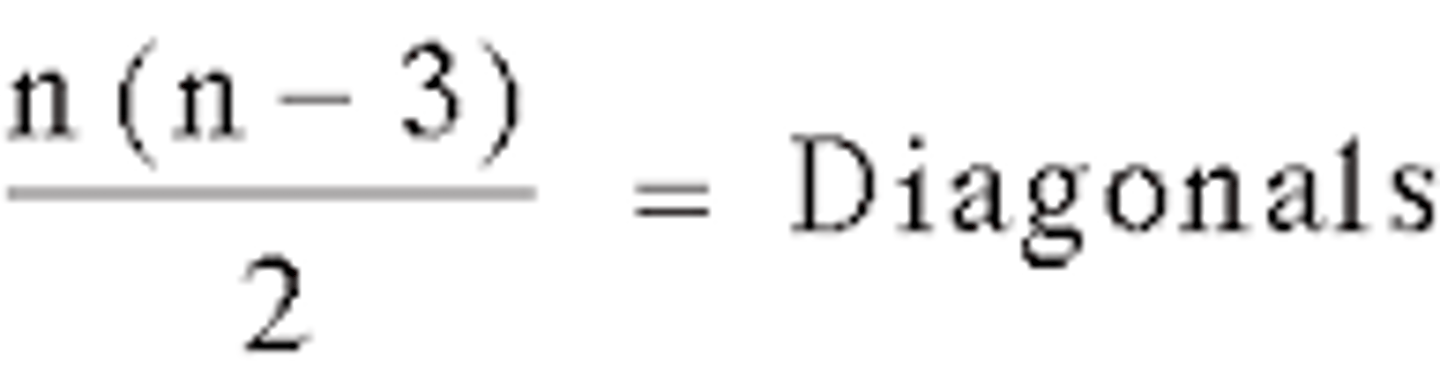
auxiliary line

a line drawn in a figure to aid in a proof

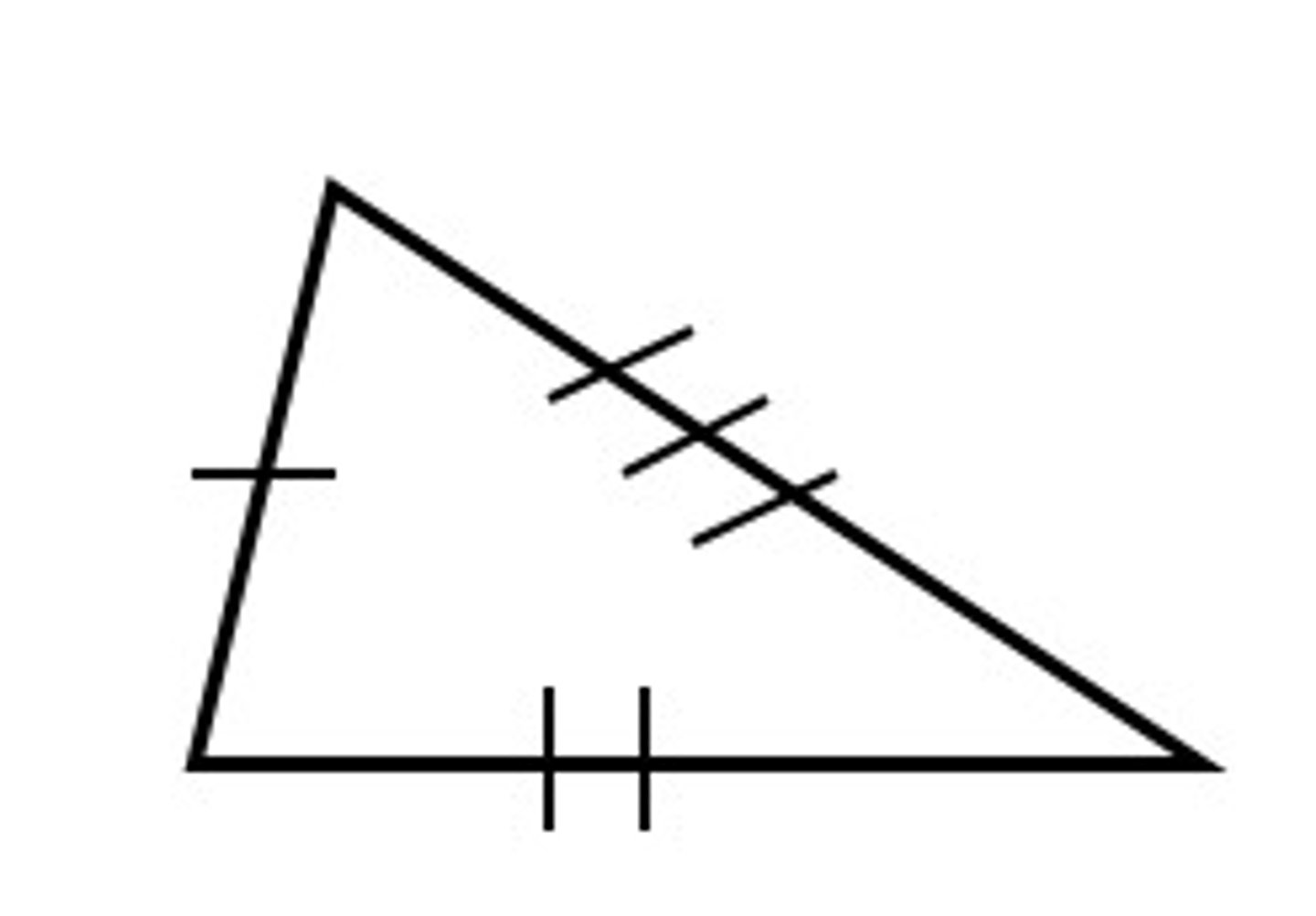
scalene triangle

a triangle with no congruent sides

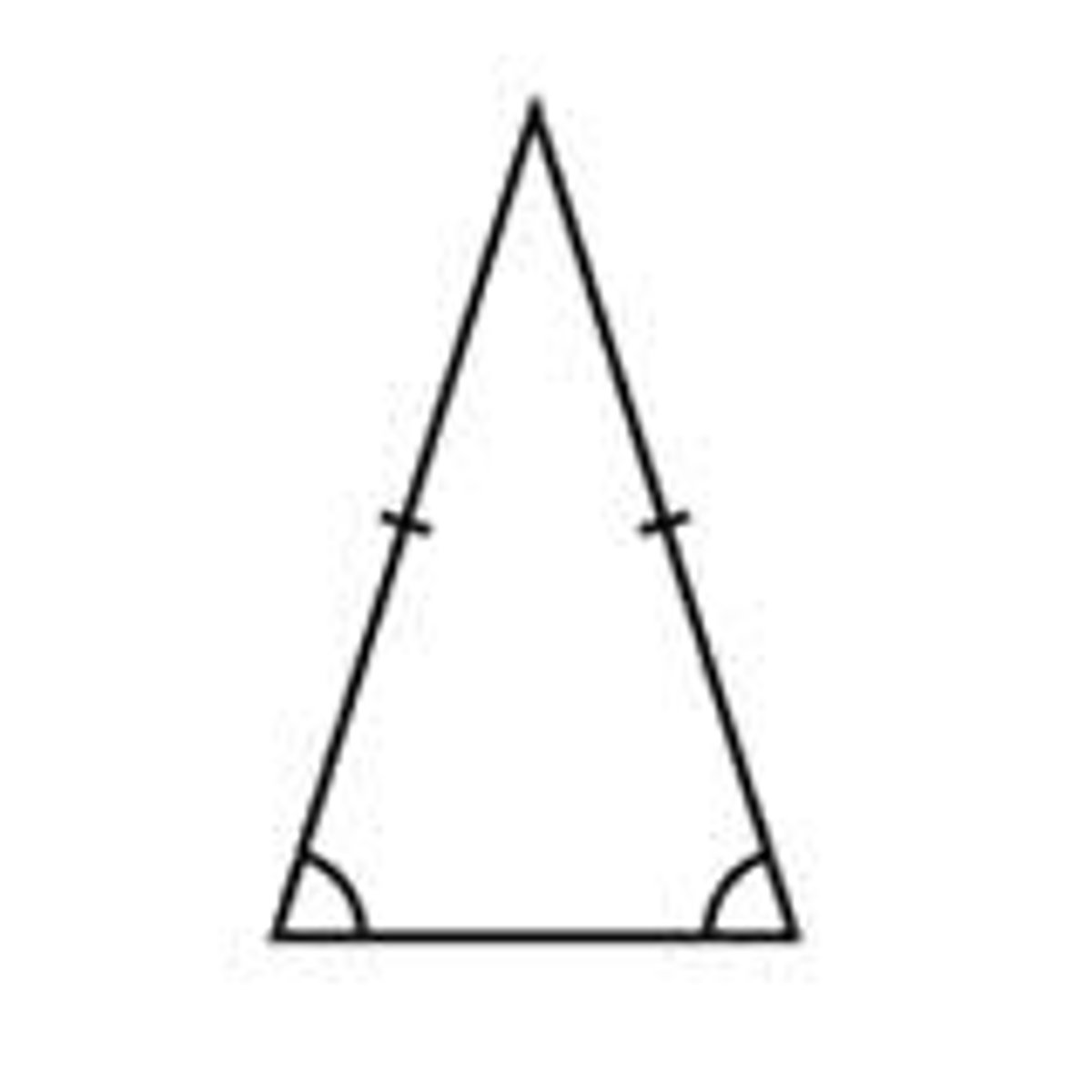
isoceles triangle

a triangle that has at least 2 congruent sides

(angles across from congruent sides are also congruent)

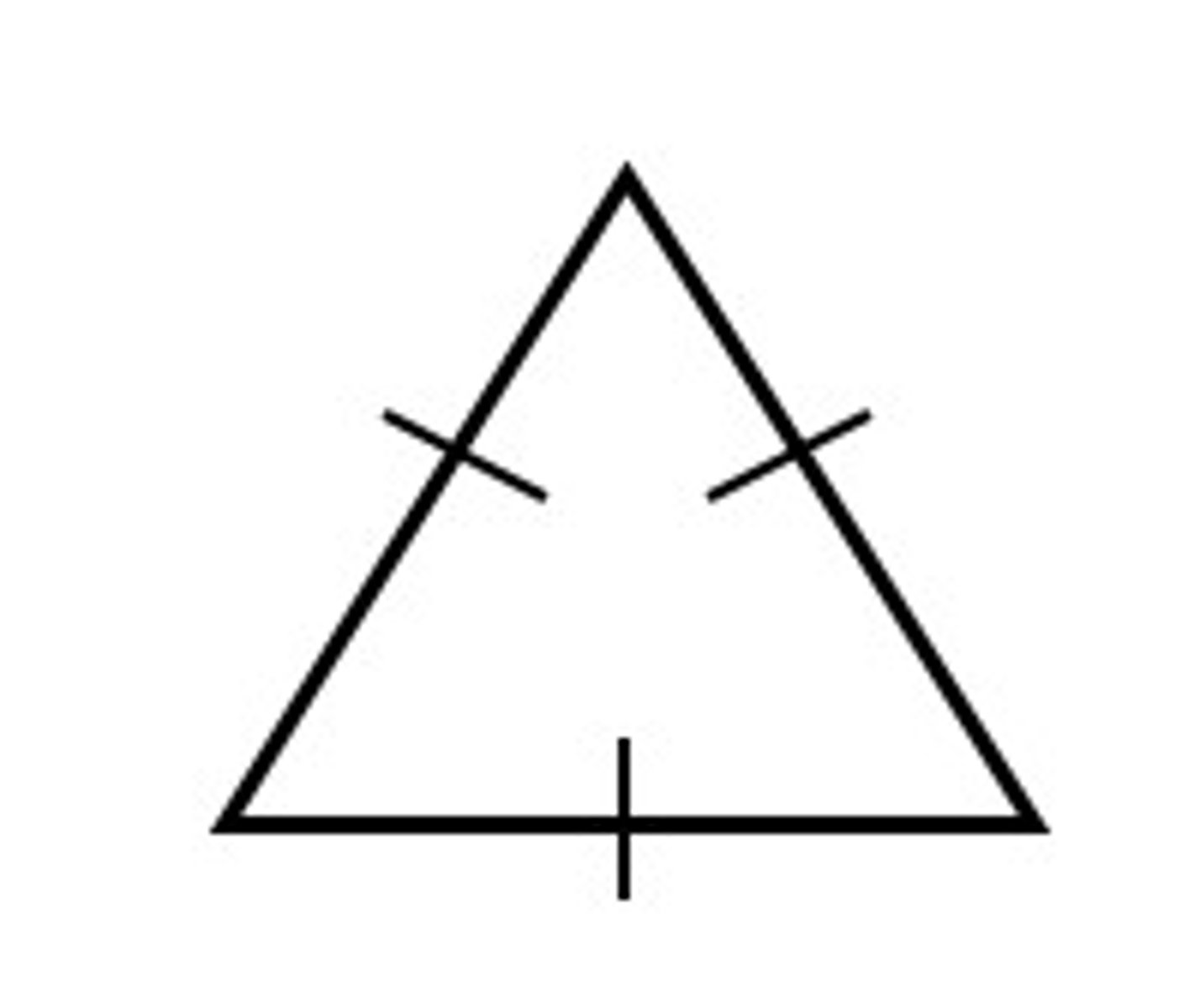
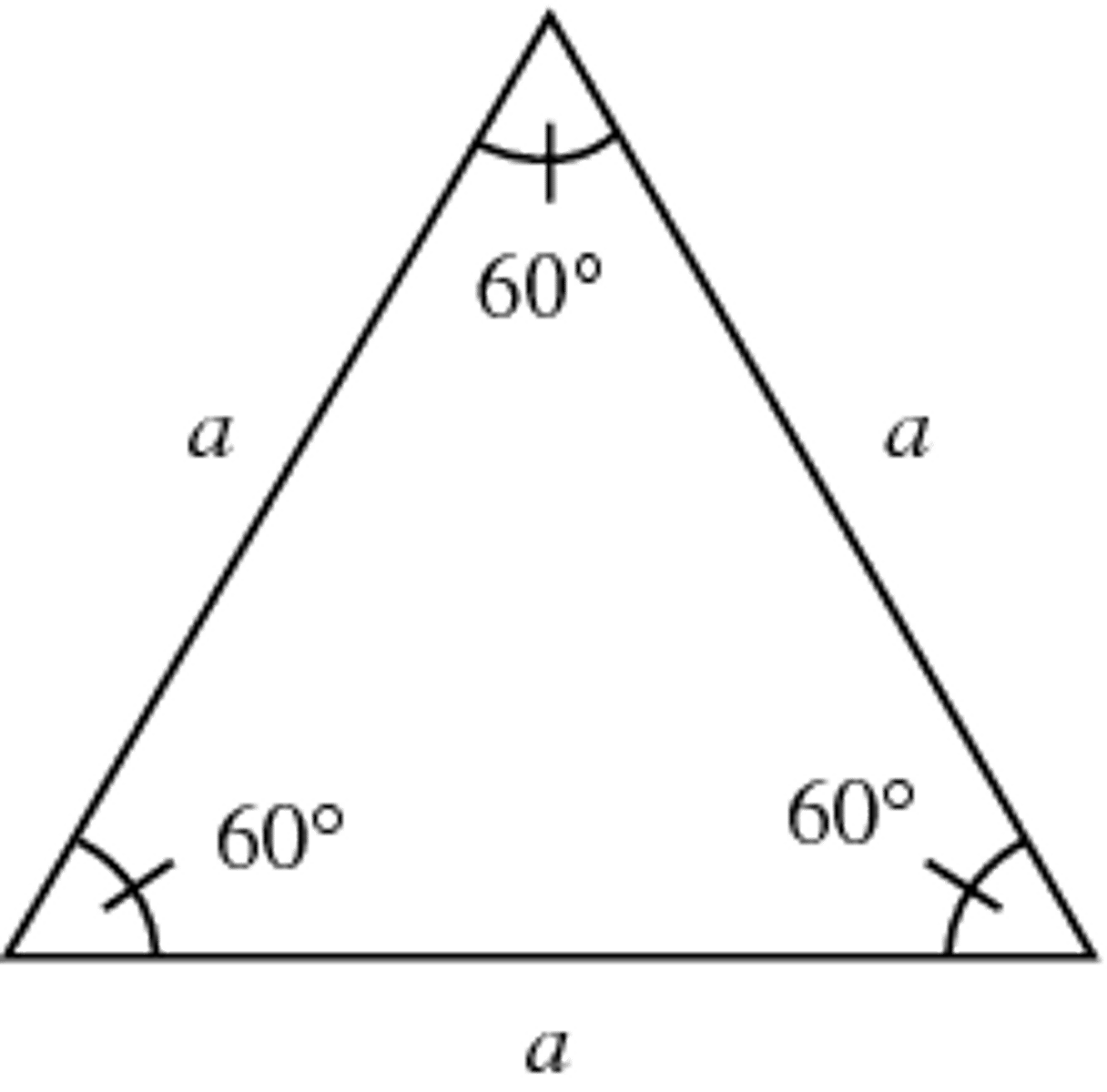
equilateral triangle

A triangle with three congruent sides

(is also isosceles)

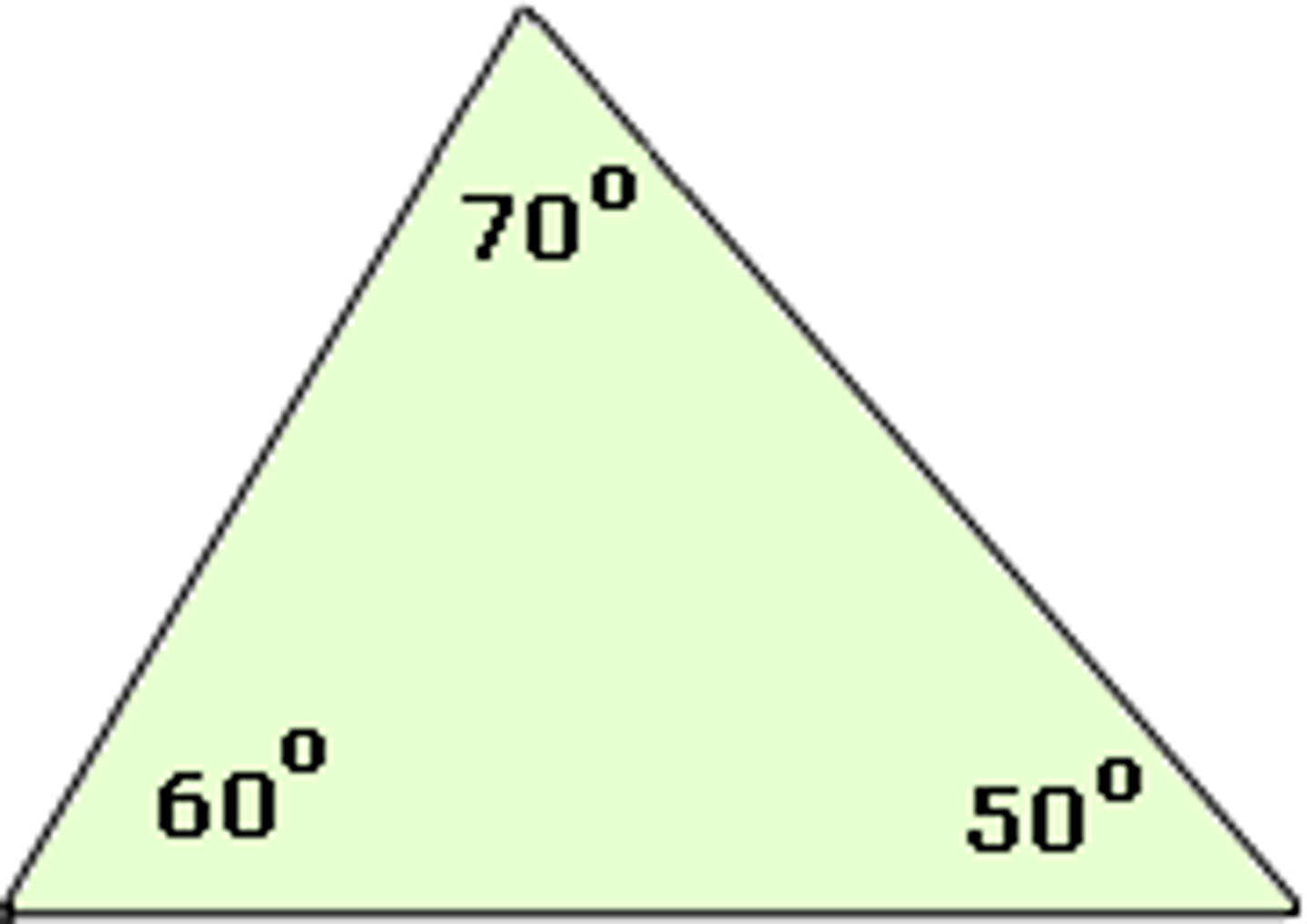
acute triangle

A triangle with 3 acute angles

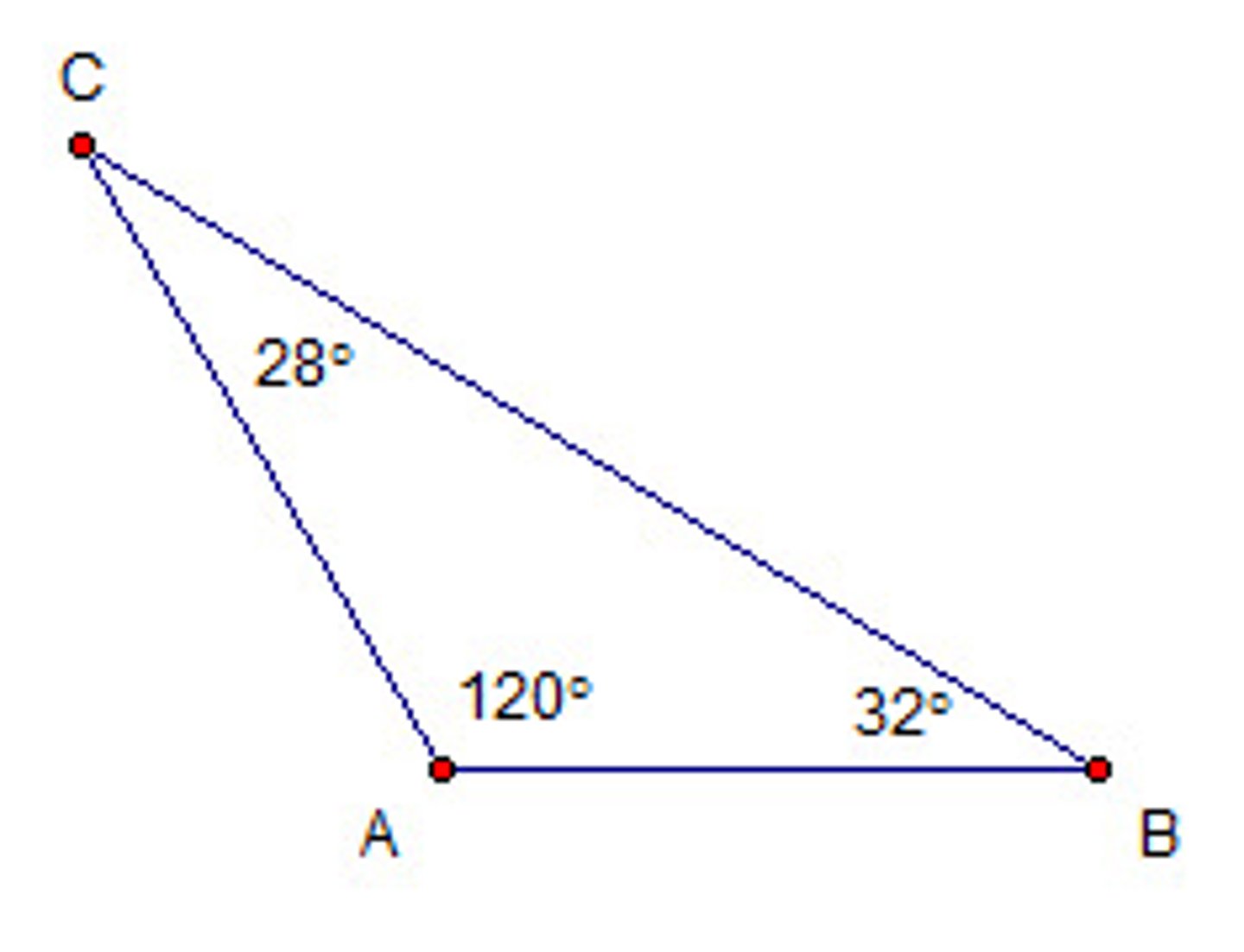
obtuse triangle

a triangle with one obtuse angle

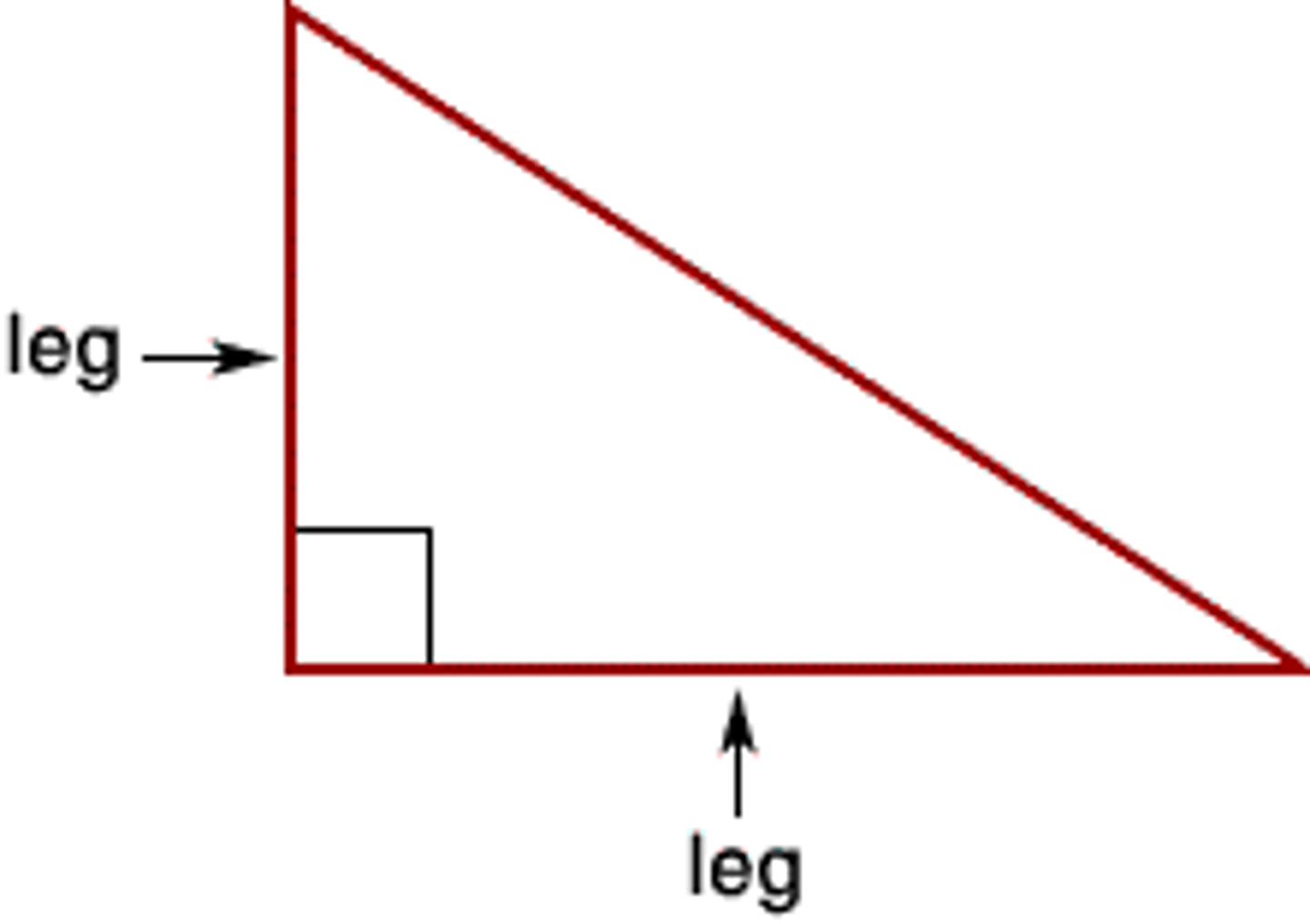
right triangle

a triangle with one right angle

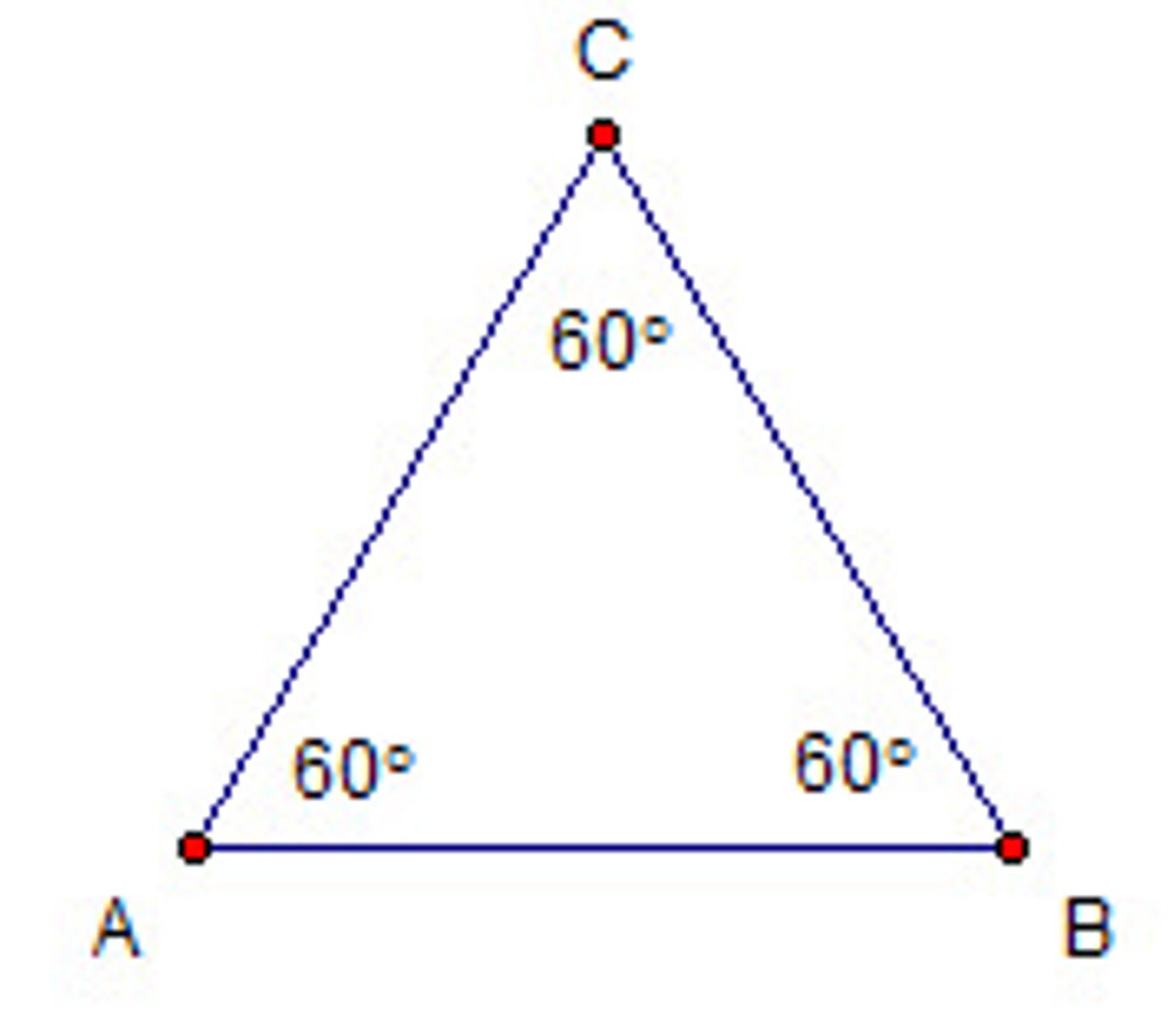
equiangular triangle

A triangle with 3 congruent angles

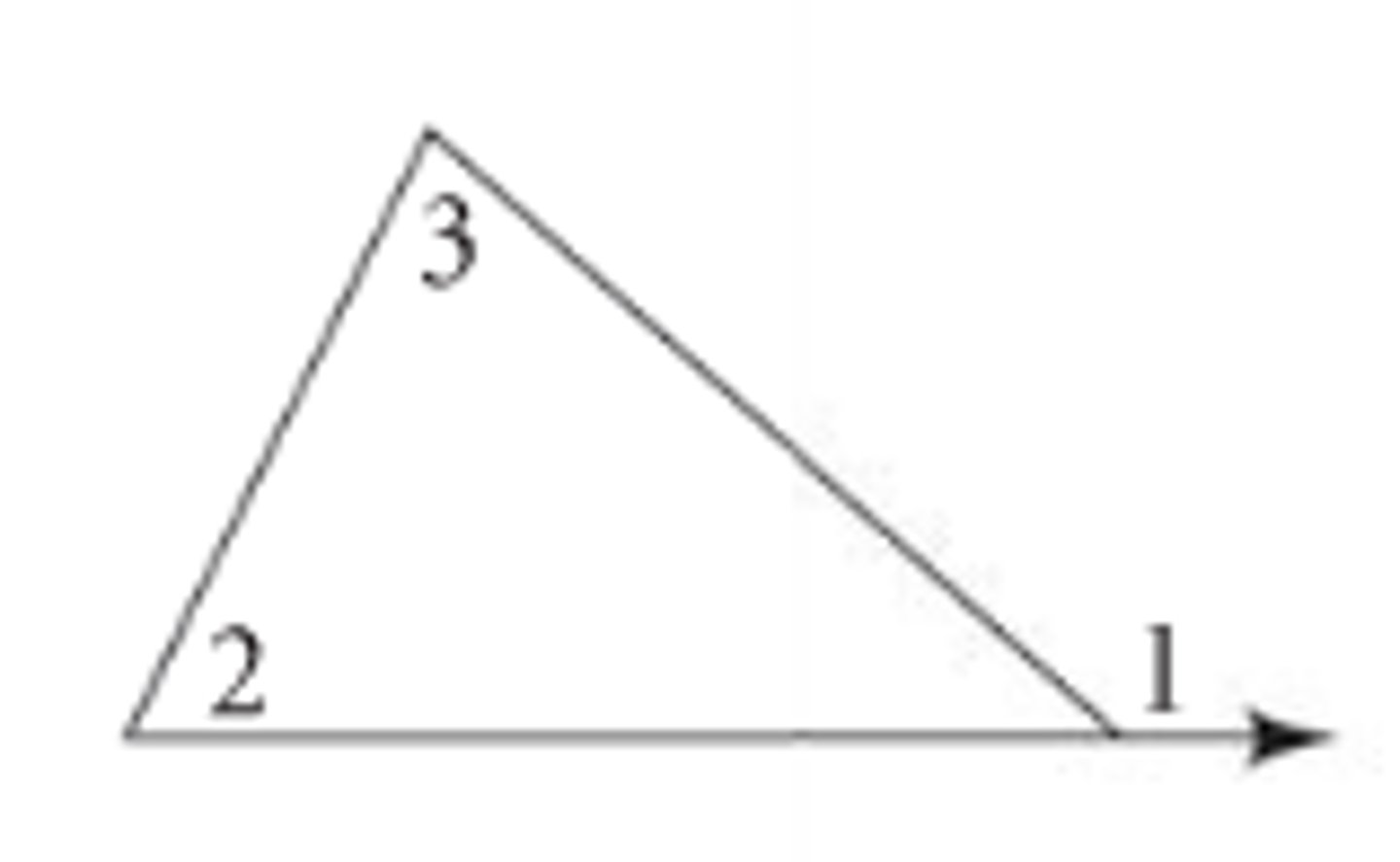
exterior angles of a shape

the angle formed when one side of the shape is extended

- adjacent interior angles is the linear angle inside the triangle

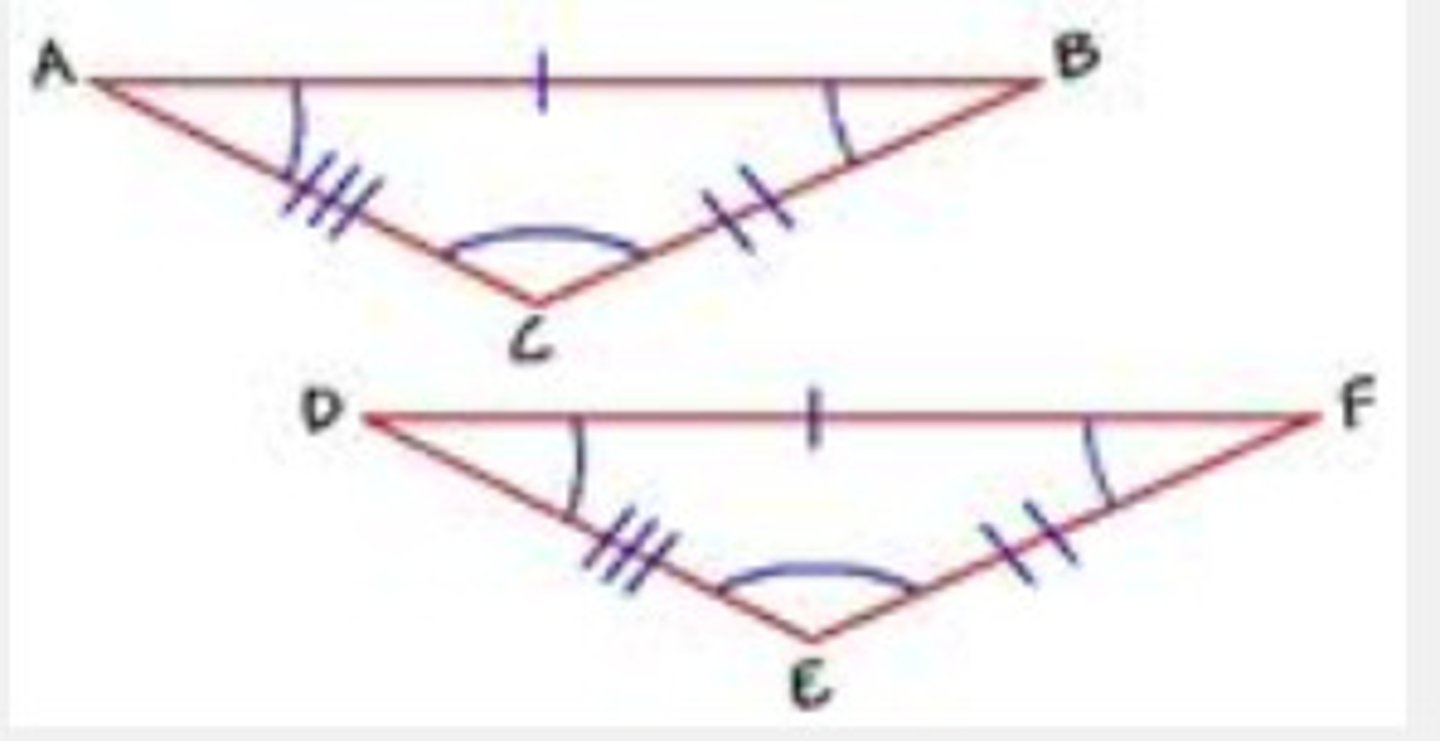
congruent figures

Figures that have the same size and shape

- when naming congruent figures, keep orientation in mind

CPCTC

corresponding parts of congruent triangles are congruent

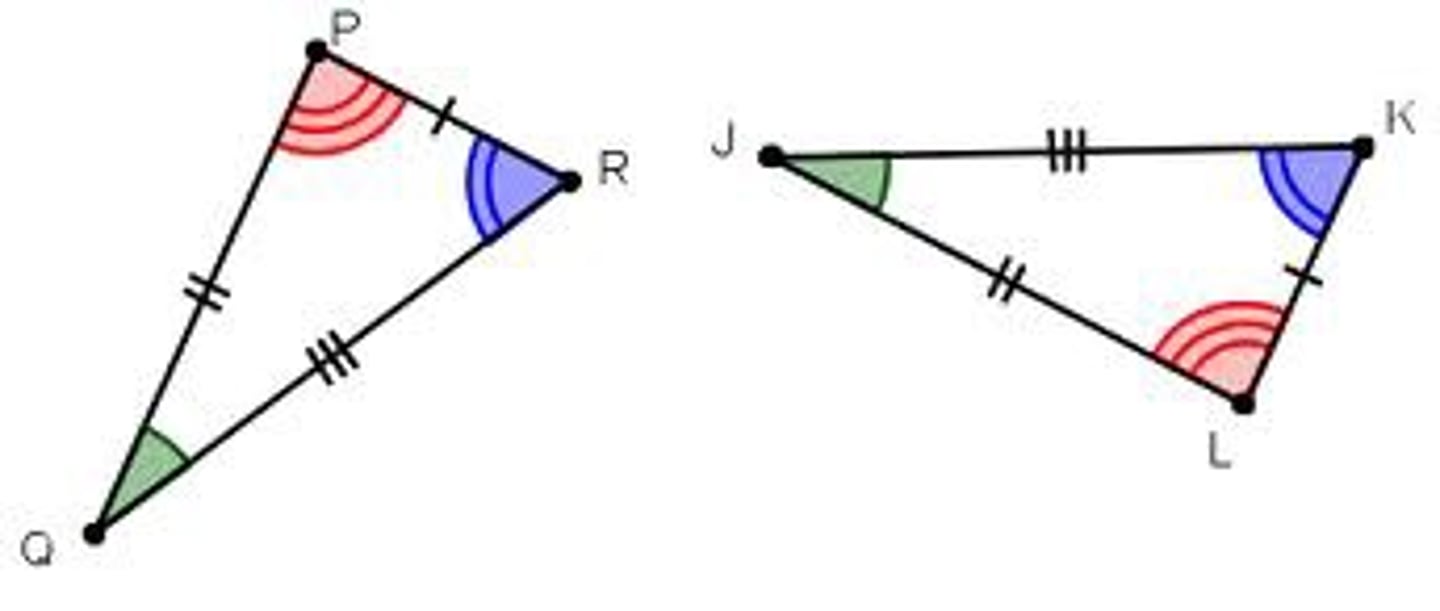
SSS Postulate (Side-Side-Side)

If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent.

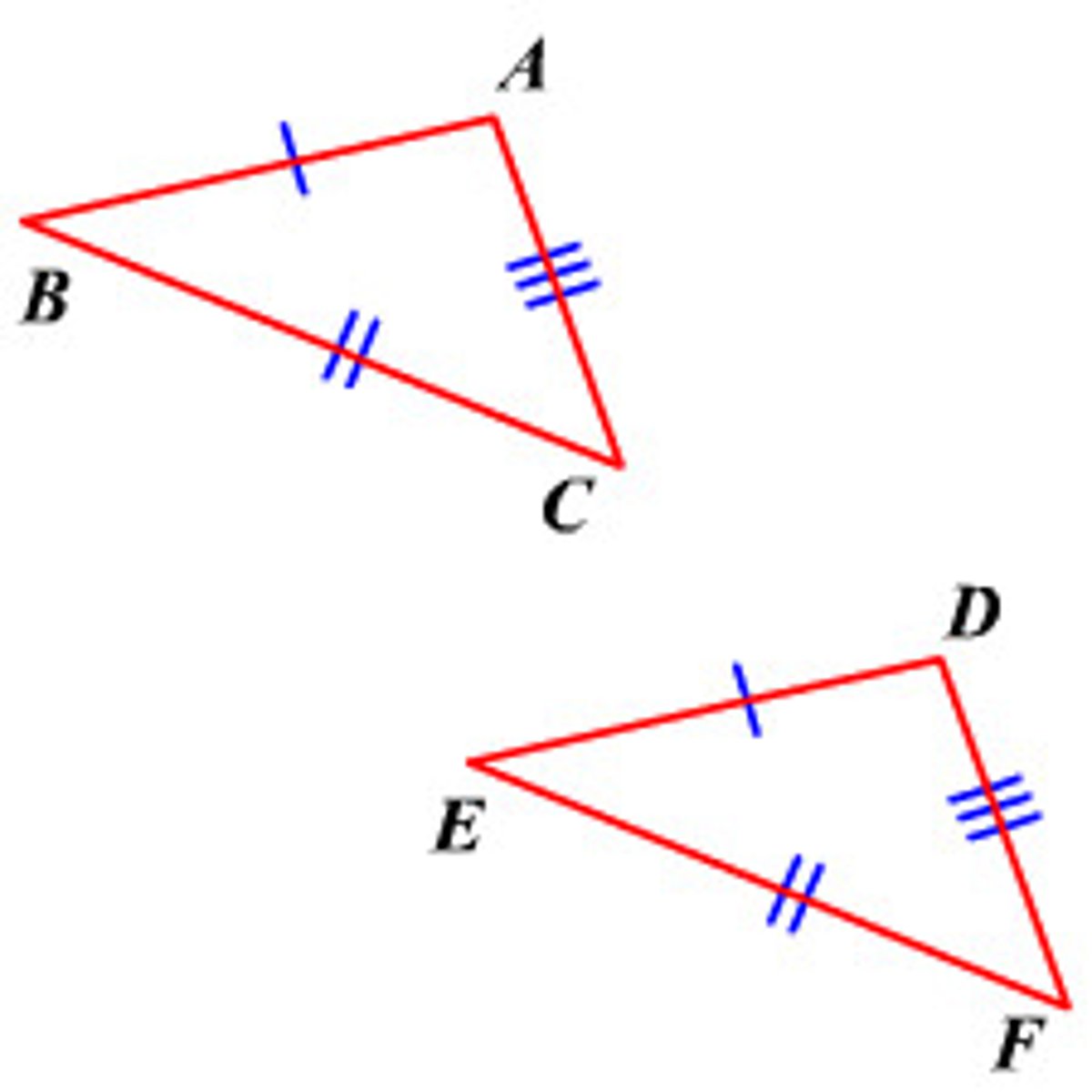
SAS Postulate (Side-Angle-Side)

If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.

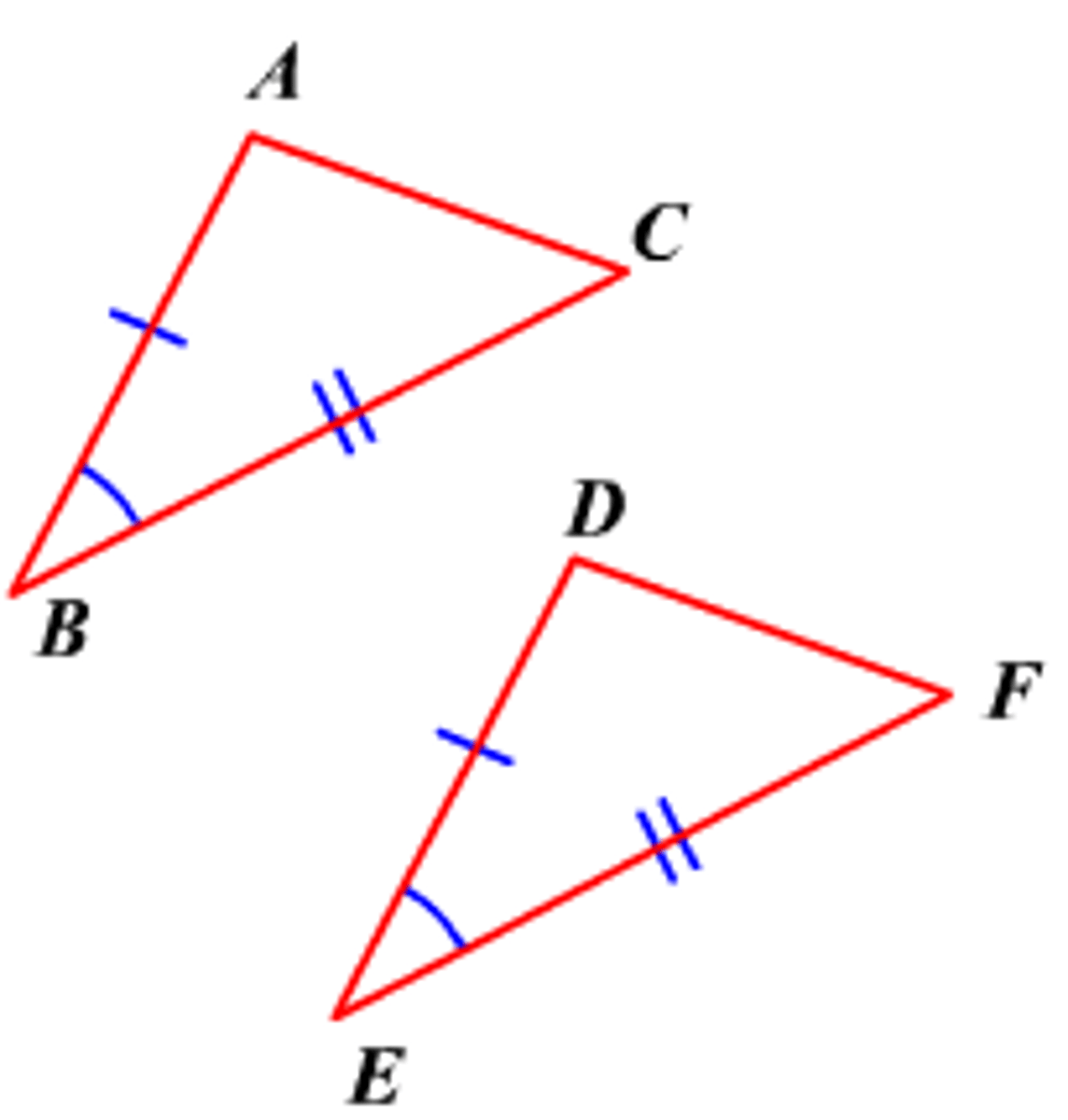
ASA Postulate (Angle-Side-Angle)

If 2 angles and the included side of 1 triangle are congruent to 2 angles and the included side of another triangle, then the triangles are congruent

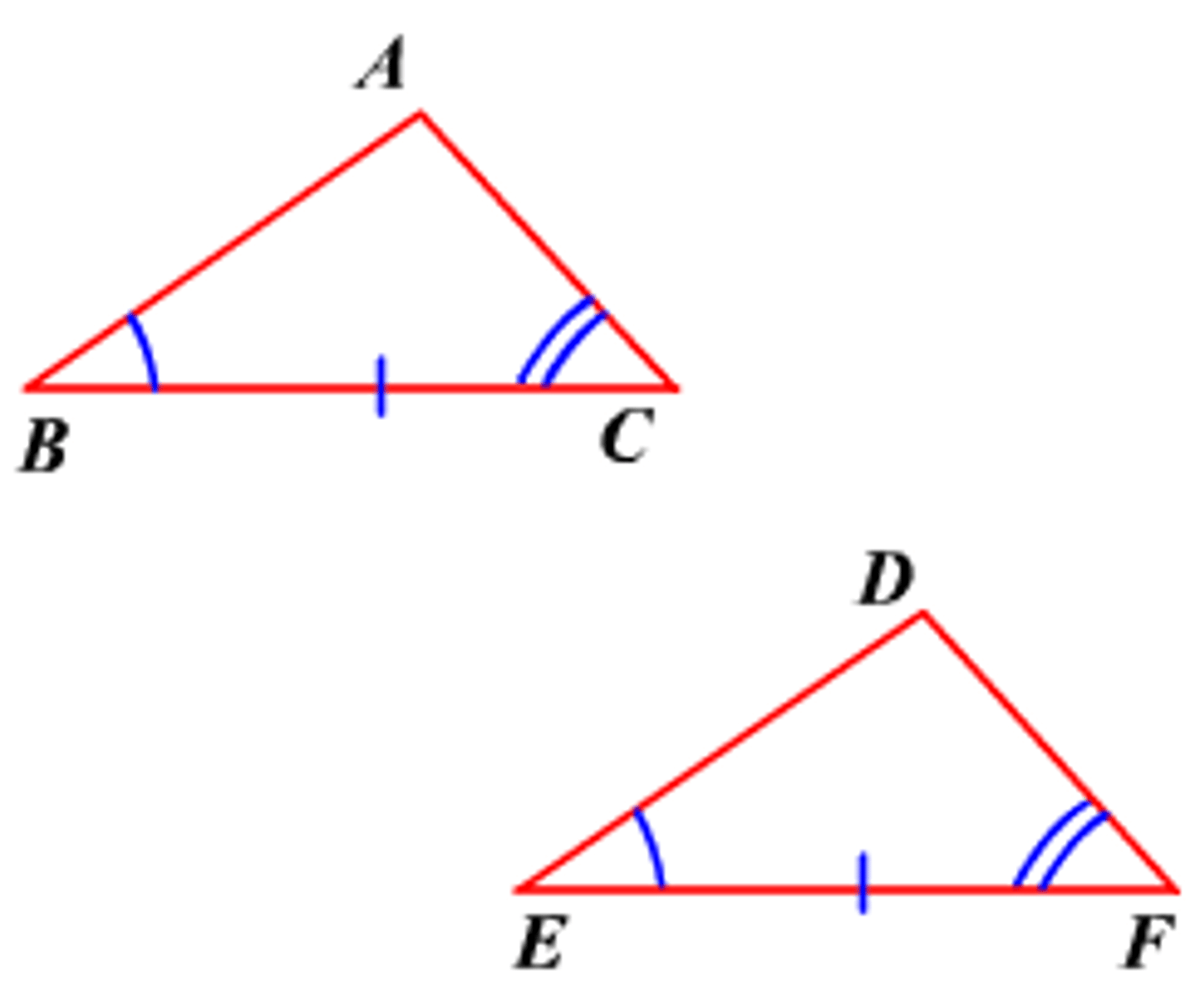
AAS Theorem (Angle-Angle-Side)

If two angles and a non-included side of one triangle are congruent to the corresponding parts of another triangle, then the triangles are congruent.

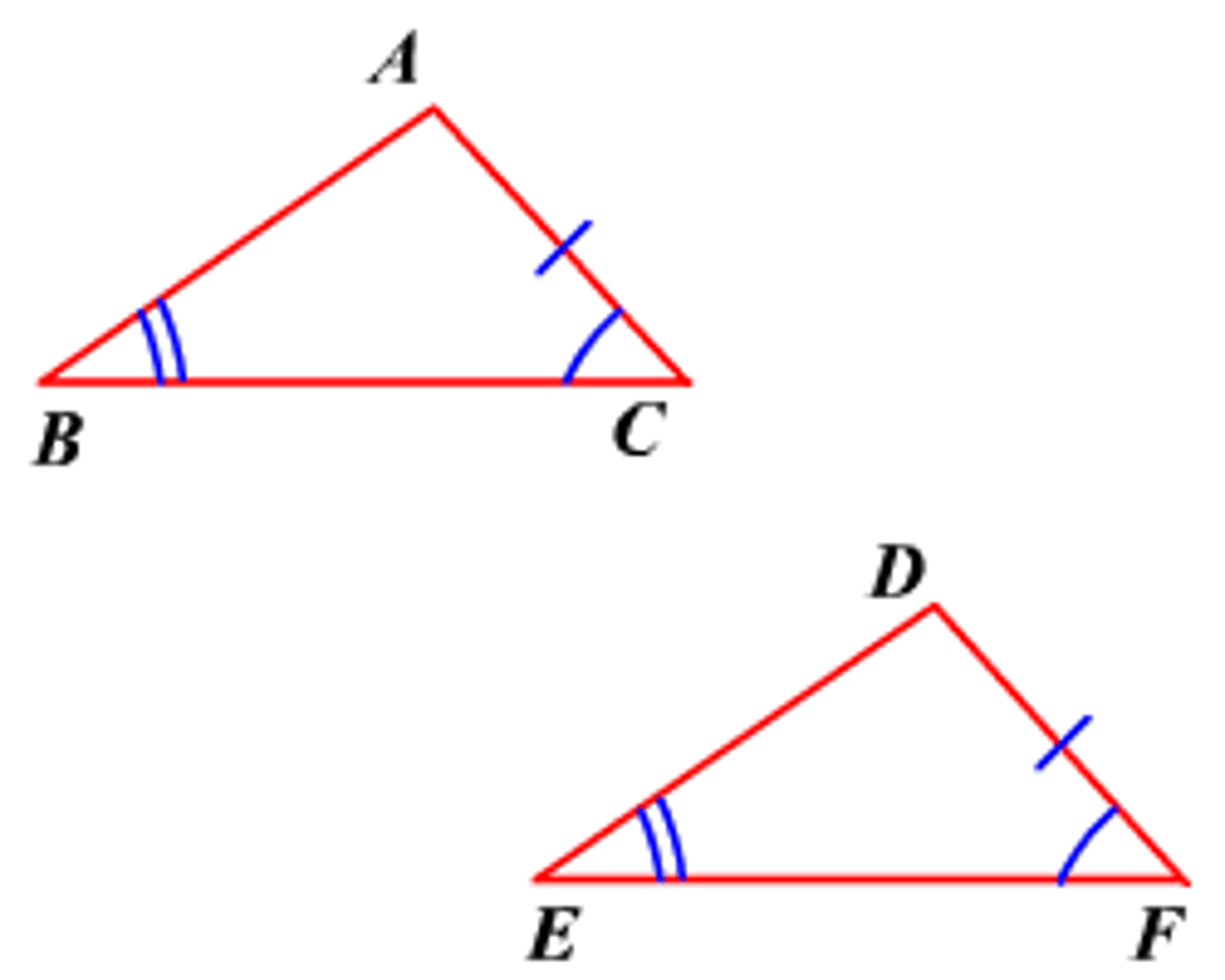
Isosceles triangle theorem

If two sides of a triangle are congruent, then the angles opposite those sides are congruent.

(works the other way around) ->

if two angles of a triangle are congruent, then the sides opposite those angles are congruent

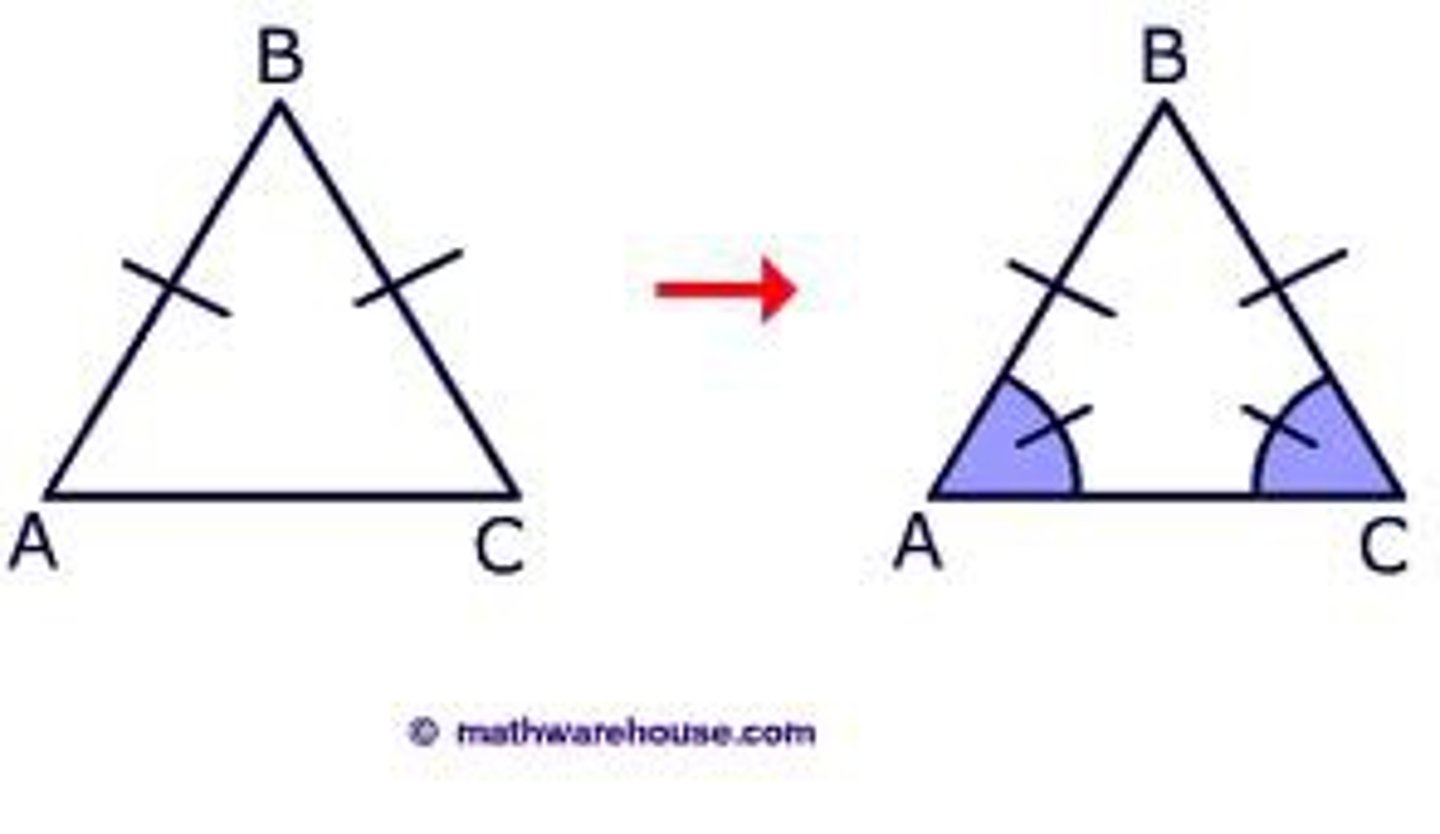
corollaries of the isosceles triangle theorem->

1. An equilateral triangle is also equiangular

2. An equilateral triangle has three 60 degree angles

3. The bisector of the vertex angle of an isosceles triangle is perpendicular to the base at it's midpoint

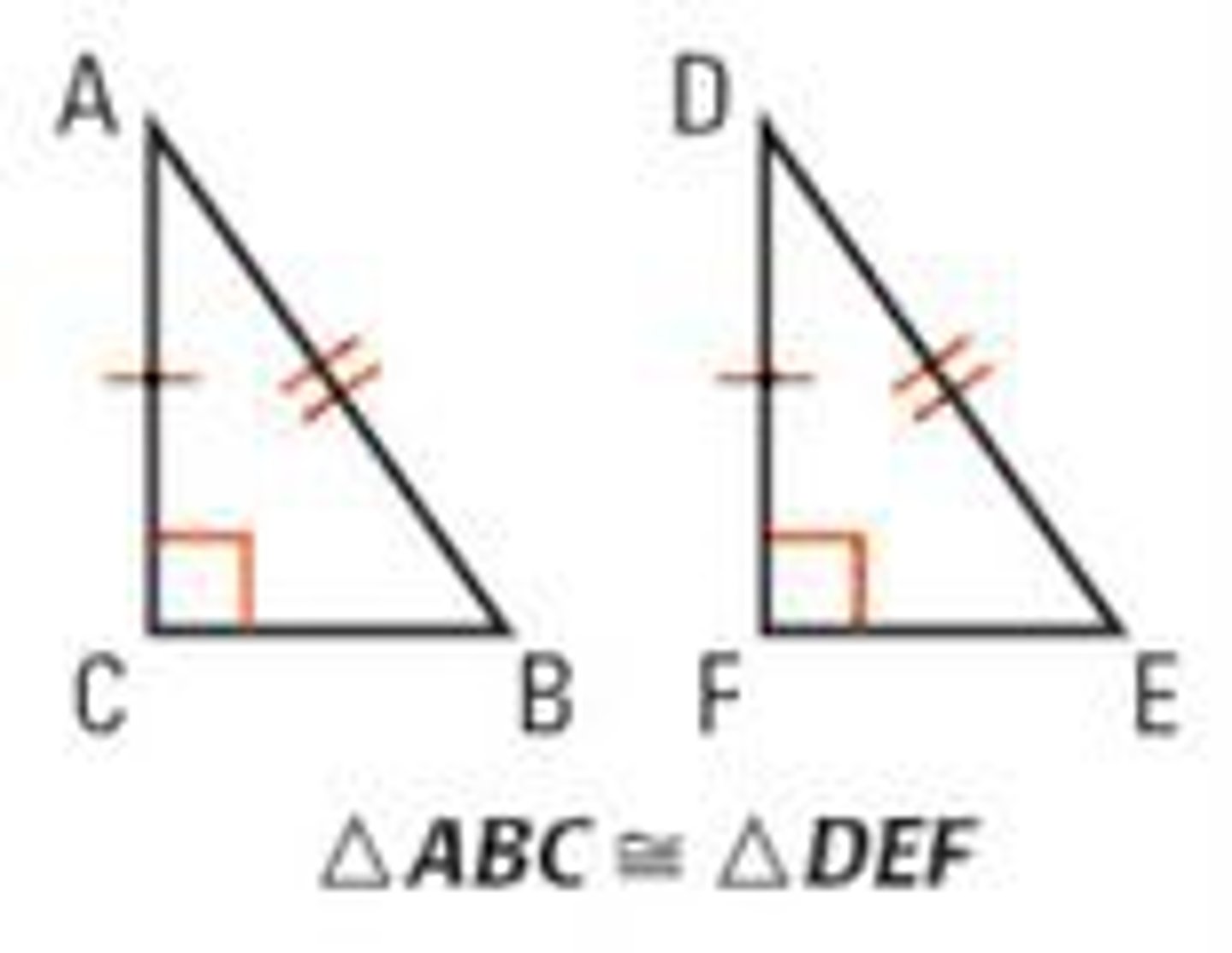
HL Theorem (hypotenuse-leg)

If the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of another right triangle, then the triangles are congruent.

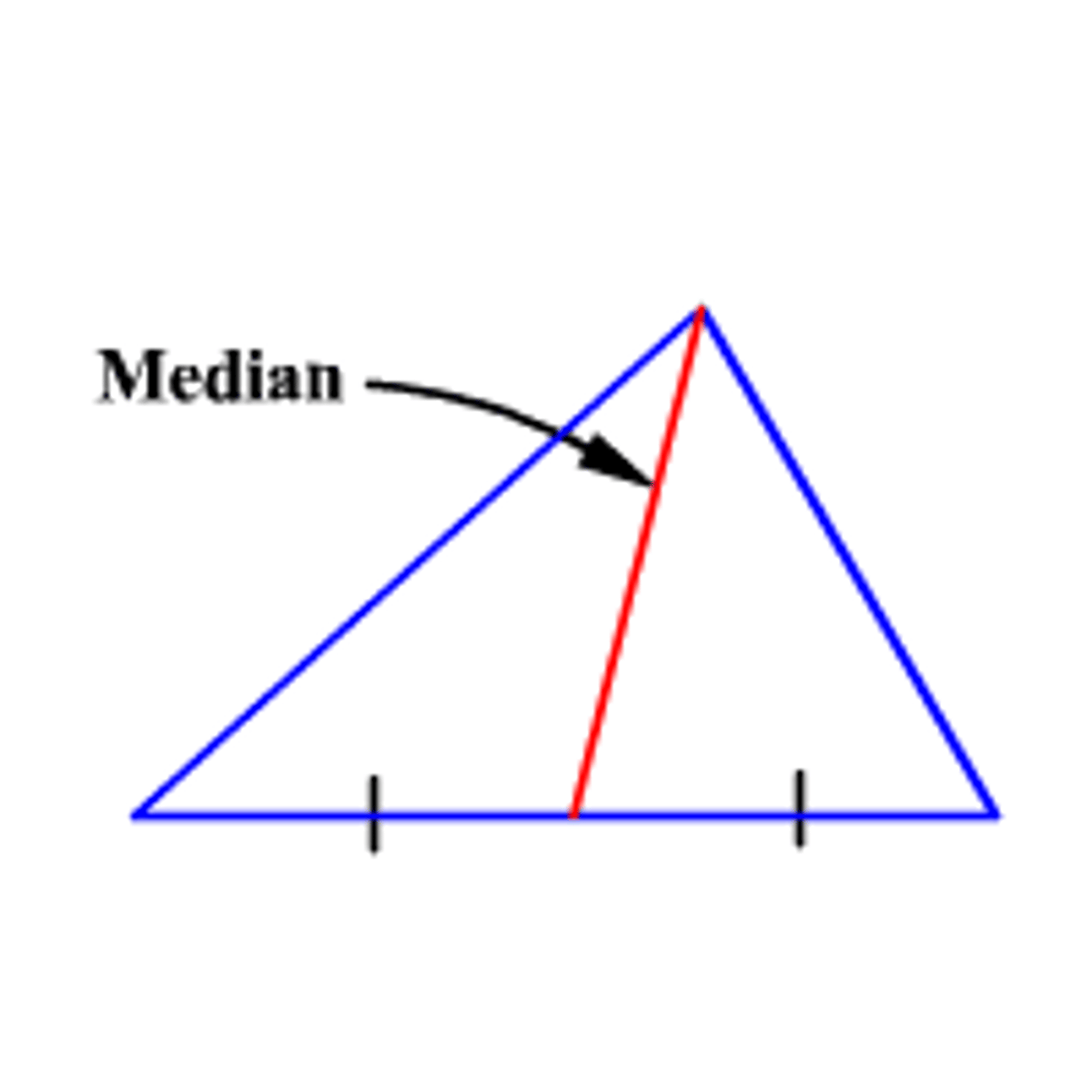
median of a triangle

a segment from a vertex to the midpoint of the opposite side

*not angle bisector

*ALWAYS IN THE TRIANGLE (SO THE INTERSECTION OF ALL MEDIAN MUST BE IN THE TRIANGLE)

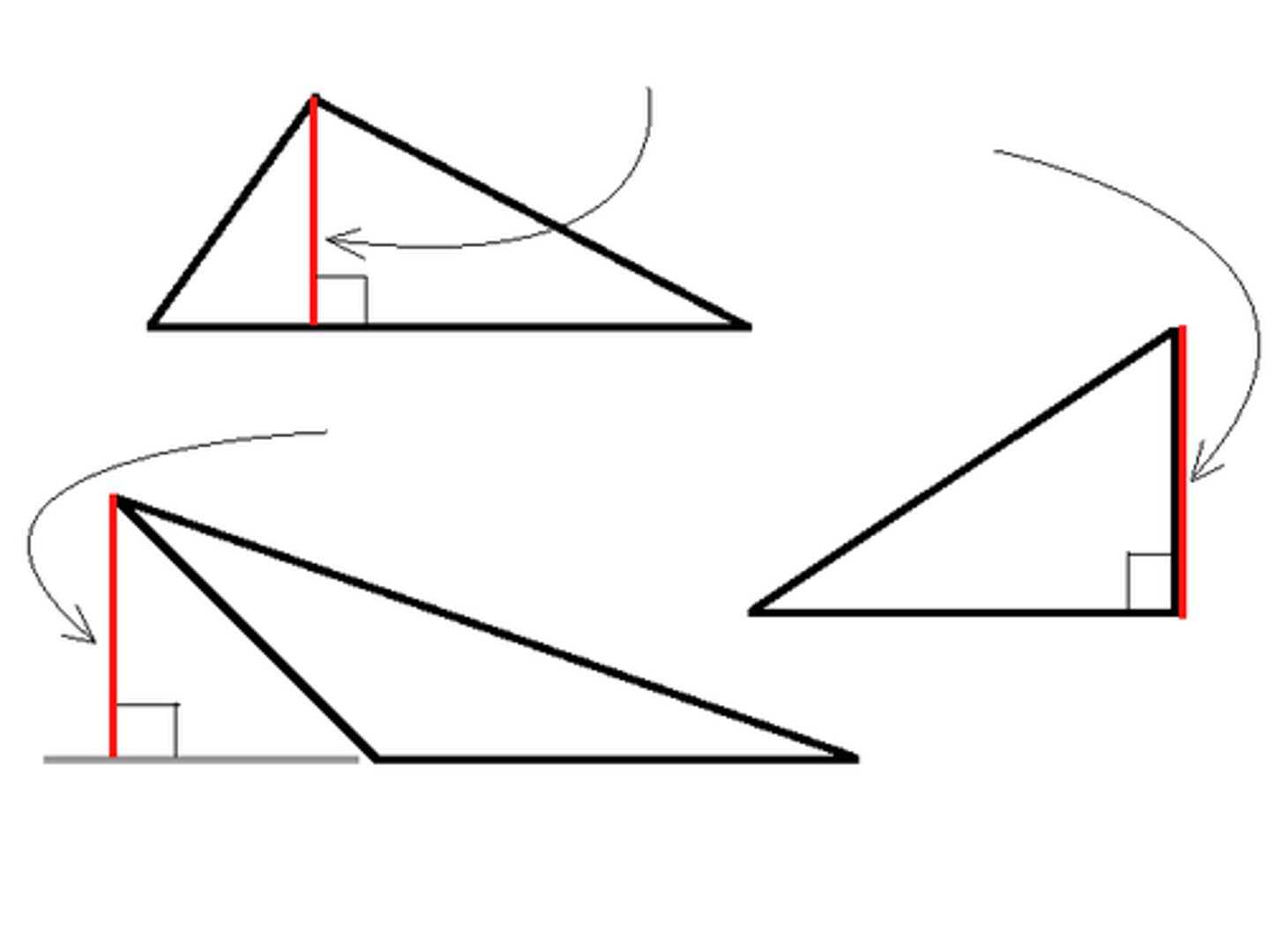
altitude of a triangle

a perpendicular segment from a vertex to the line containing the opposite side

*in isosceles triangles, (so that the altitude is between congruent sides) the altitude is also the median, the angle bisector, and perpendicular bisector.

*is not always in the triangle

perpendicular bisector

A line that is perpendicular to a segment at its midpoint.

-for obtuse triangles, the intersection is OUTSIDE the triangle.

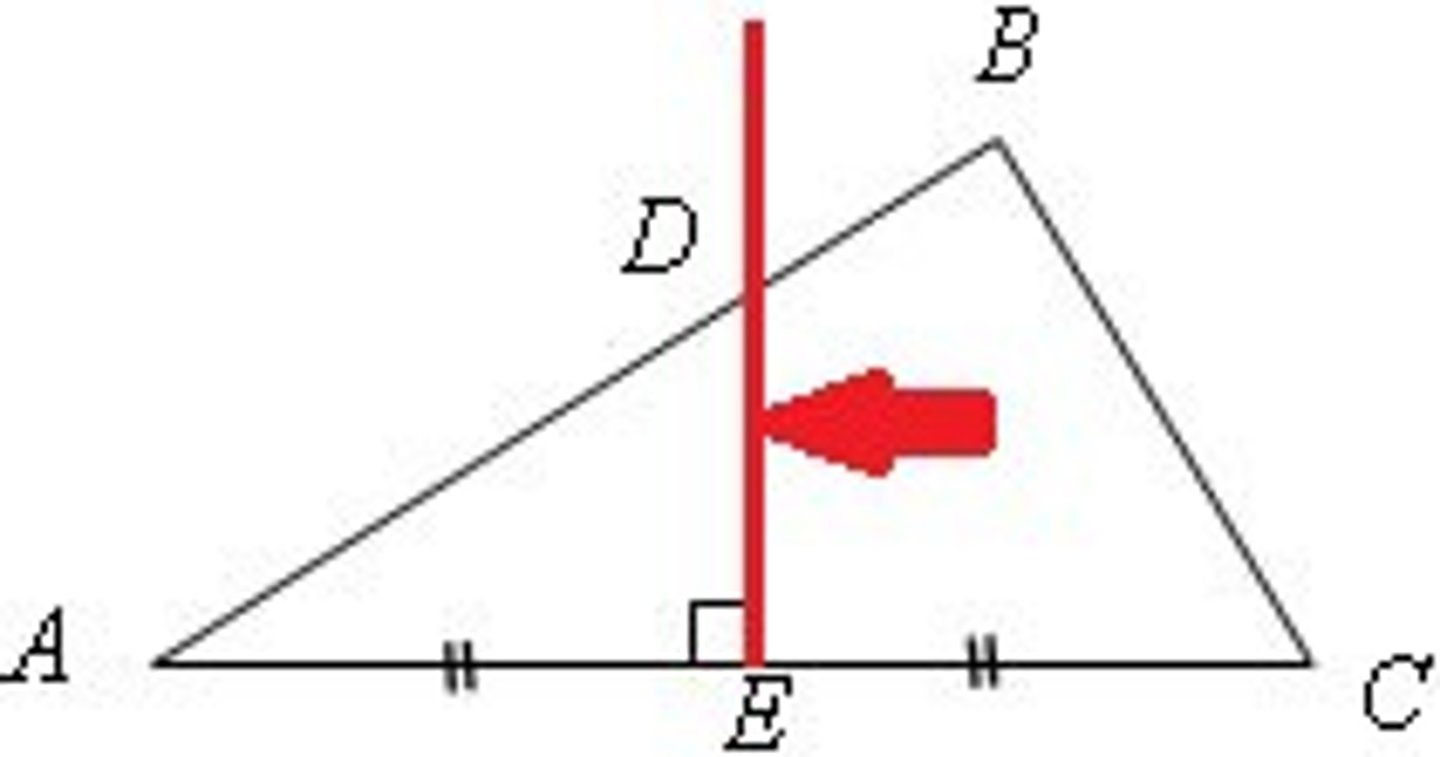
Equidistant theorems #1 and #2

- perpendicular bisector of a segment

1) If a point lies on the perpendicular bisector of a segment, then it is equidistant from the endpoint of a segment.

2) if a point is equidistant from the endpoints of a segment, then the point lies on the perpendicular bisector of the segment.

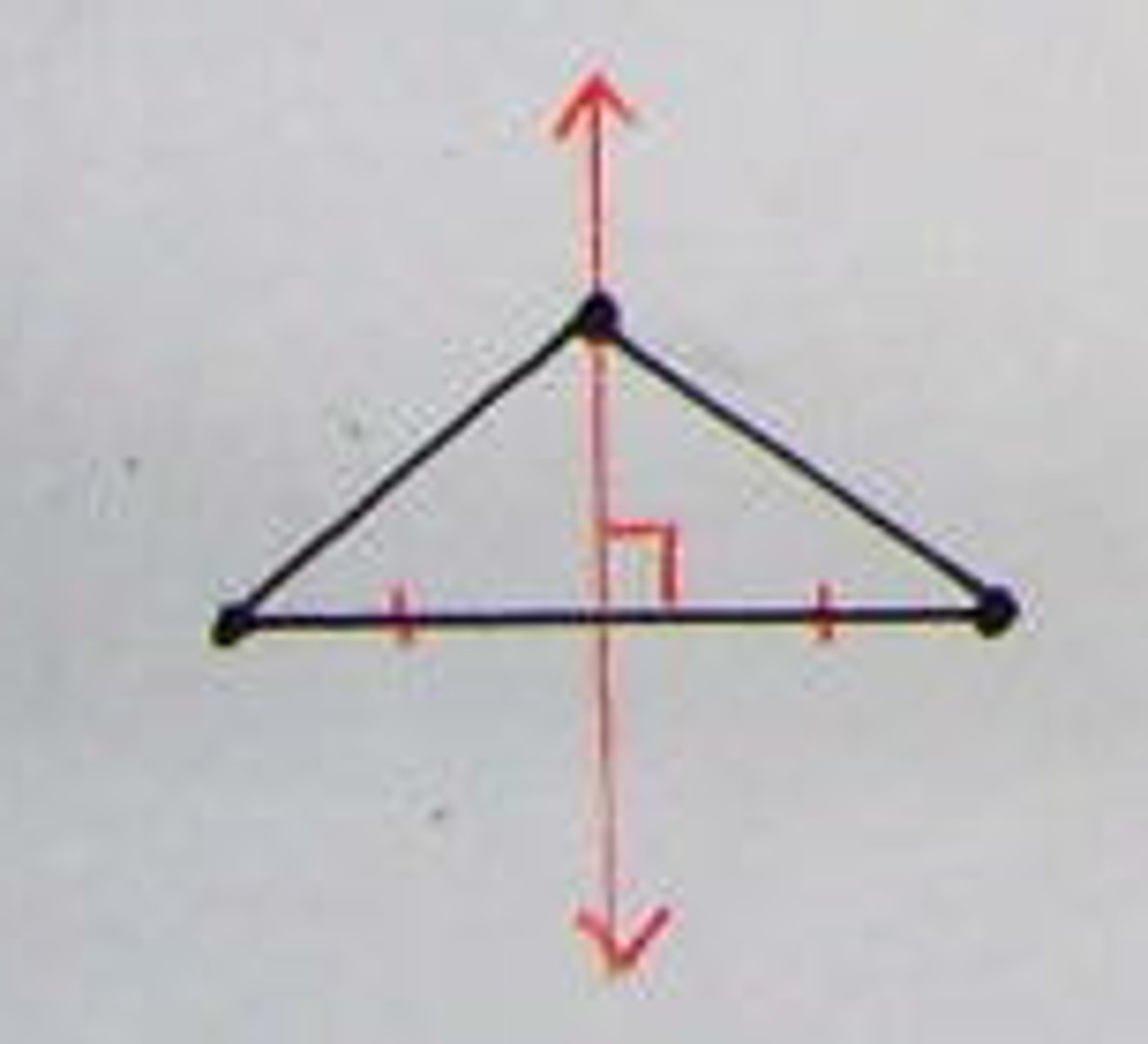
Equidistant Theorems #3 and #4

- Angle Bisector

3) if a point lies on the bisector of an angle, then the point is equidistant from the sides of the angle.

4) If a point is equidistant from the sides of an angle, then the point lies on the angle bisector.

A whole is _______ than its parts.

greater

Trichotomy Postulate

exactly one of the following is true (for real numbers): a>b or a=b or a