Operations Management chap 5, 6, 7, 8, 11, 16

Final definition study guide.

What are the three types of Integer Programming Models?

Total Integer Model, 0-1 (Binary) Integer Model, and Mixed Integer Model.

What is a Total Integer Model?

A model where all decision variables are required to be integers.

What is a 0-1 (Binary) Integer Model?

A model where all decision variables are constrained to be either 0 or 1 (typically used for 'yes/no' decisions).

What is a Mixed Integer Model?

A model where some decision variables are required to be integers, while others can be non-integers (continuous).

Traditional approach used to solve integer programming problems?

The Branch and Bound Method.

What is the primary issue with rounding non-integer solutions in Integer Programming?

Rounding can lead to solutions that are either infeasible or sub-optimal compared to the true integer optimum.

How does rounding a non-integer solution up affect an IP problem?

Rounding a non-integer solution up can frequently lead to a solution that violates one or more constraints, making it infeasible.

How does rounding a non-integer solution down affect an IP problem?

Rounding a non-integer solution down usually results in a feasible solution, but it is often sub-optimal (less than the best possible value).

What is the difference between a Mixed Integer Model and a Total Integer Model?

In a Mixed Integer Model, only a subset of decision variables must be integers, whereas in a Total Integer Model, all variables must be integers.

Integer Programming Graphical Solution always guarantees the optimality of an obtained solution.

False

Branch and Bound Method

Feasible solutions can be partitioned into smaller subsets and the smaller subsets are evaluated until best solution is found.

Branch and Bound Method Drawbacks

Method is a tedious and complex mathematical process.

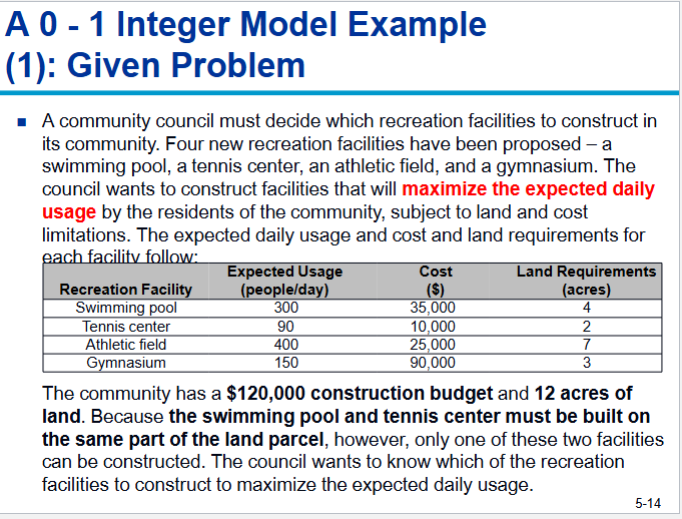
Chap 5 slide 14 example of a integer model. Solve.

Decision Variables: x1 = a swimming pool, x2 = a tennis center, x3 = an athletic field, and x4 = a gymnasium

OBJ func: Max Z= 300x1 + 90x2 + 400x3 + 150x4

Constraints:

Budget of $120,000-

35,000x1 + 10,000x2 + 25,000x3 + 90,000x4 <= 120,000

Available lands-

4x1 + 2x2 + 7x3 + 3x4 <= 12 acres

Designated land parcel for the swimming pool or tennis center=-

x1 + x2 <= 1

Constraints for decision variables-

x1, x2, x3, x4 =0 or 1

Transportation Model

A mathematical model used to determine the most cost-effective way to transport goods from multiple suppliers to multiple consumers, while satisfying supply and demand constraints.

Resource Allocation Optimization for Transportation problem.

A product is transported from a number of sources to a number of destinations at the minimum possible cost.

The linear programming model has constraints for supply at each source and demand at each destination.

-Each source is able to supply a fixed number of units of the product, and each destination has a fixed demand for the product.

Types of Transportation Model: Balanced.

All constraints are equalities and supply = demand.

Types of Transportation Model: Unbalanced.

Constraints have inequalities in them and supply does not equal demand.

The Transshipment Model Characteristics

Extension of the transportation model.

Intermediate transshipment points are added between the sources and destinations.

For a transhipment model, items can be transported from:

• Sources through transshipment points to destinations

• One source to another

• One transshipment point to another

• One destination to another

• Directly from sources to destinations

• Some combination of these

Assignment model

• Special form of linear programming model similar to the transportation model.

• Supply at each source and demand at each destination limited to one unit.

Transhipment example problem: network routes

Number of tons of wheat transported from location i to j =X_ij

_{For ij= (i, j)= (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 6), (3,7), (3, 8), (4, 6), (4, 7), (4, 8), (5, 6), (5, 7), (5, 8)}

Obj Func:

Min Z= 16_×13 + 10_×14 + 12_×15 + 15x₂₃ + 14x₂₄ + 17x₂₅ + 6x₃₆ + 8x₃₇ + 10x₃₈ + 7x₄₆ + 11x₄₇ + 11x₄₈ + 4x₅₆ + 5x₅₇ + 12x₅₈

S.T.

Sources-

x₁₃ + x₁₄ + x₁₅ = 300

x₂₃ + x₂₄ + x₂₅ = 300

Destinations

x₃₆ + x₄₆ + x₅₆ = 200

x₃₇ + x₄₇ + x₅₇ = 100

x₃₈ + x₄₈ + x₅₈ = 300

Transshipments

x₁₃ + x₂₃ - x₃₆ - x₃₇ - x₃₈ = 0

x₁₄ + x₂₄ - x₄₆ - x₄₇ - x₄₈ = 0

x₁₅ + x₂₅ - x₅₆ - x₅₇ - x₅₈ = 0

x_ij >= 0

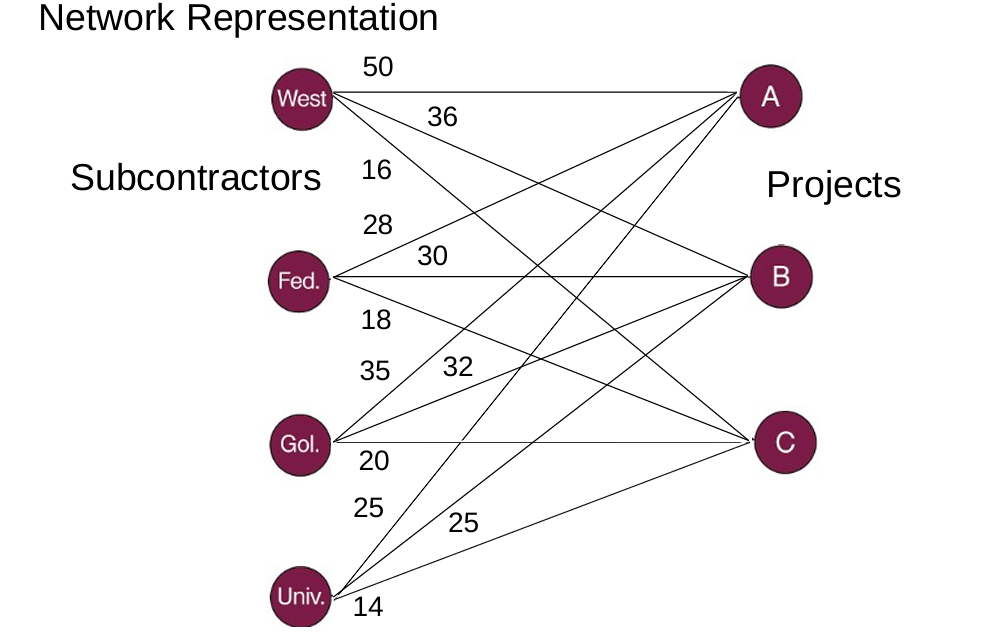
Assignment Problem: Example

LP formulazation:

Min Z= 50x₁₁ +36x₁₂ +16x₁₃ +28x₂₁ +30x₂₂ +18x₂₃ +35x₃₁ +32x₃₂ +20x₃₃ +25x₄₁ +25x₄₂ +14x₄₃

S.T.:

x₁₁ + x₁₂ + x₁₃ <= 1

x₂₁ + x₂₂ + x₂₃ <=1

x₃₁ + x₃₂ + x₃₃ <=1

x₄₁ + x₄₂ + x₄₃ <=1

xij = 0 or 1 for all I and j