Chapter 1: Mathematics and Measurements

1.1 Orders of Magnitude and Significant Figures:

In physics, we use a range of magnitudes, from very, very big to very, very small. To easily express these we write them to the power of ten (for example 10000 would be written as 10^4).

• 10 = 10^1

• 100 = 10²

• 1000 = 10³

• 10000 = 10^4

• 100000 = 10^5

1.2 Uncertainties:

The uncertainty is an estimate of the difference between the measurement reading and the true value. The two types of measurement errors that can lead to uncertainties are random and systemic errors.

• random error: unpredictable fluctuations in measurement readings due to uncontrolled factors.

• systematic error: due to the use of faulty systems or flaws in the experimental method

There are three different types of uncertainties:

• absolute uncertainty: when uncertainty is given as a fixed quantity

• fractional uncertainty: when uncertainty is given as a fraction of the total measurement

• percentage uncertainty: when uncertainty is given as a percentage of the total measurement

There are different uncertainties in different situations:

• in a reading: ± half the smallest division

• in a measurement: ± the smallest division

• in repeated data: half the range (i.e. +-1/2(largest-smallest value)

• in a digital reading: ± the last significant digit unless otherwise quoted

• in the natural log of a value: uncertainty in x divided by x

Combining uncertainties:

• addition and subtraction: y=a+b or y=a-b

  • Δy = Δa + Δb (the sum of the absolute uncertainties)

• multiplication and division: y=ab or y=a/b

  • Δy/y = Δa/a + Δb/b (the sum of the fractional uncertainties)

• power: y=a^n

  • Δy/y = n(Δa/a) (the magnitude of n times the fractional uncertainty)

1.3 Scalars and Vectors:

A scalar is a quantity that has magnitude and a vector is a quantity that has both magnitude and direction. Distance is a scalar quantity and displacement is a vector quantity as only displacement accounts for the direction that the movement is in.

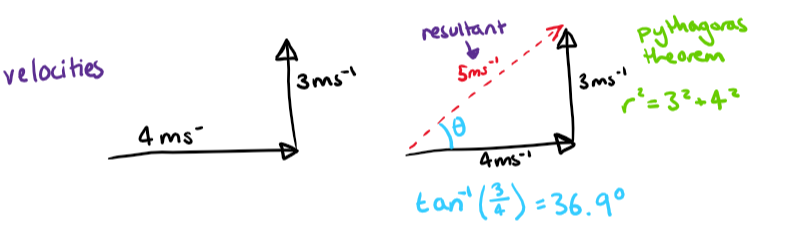
Vectors are represented by arrows. The arrowhead indicates the vector's direction and the arrow's length indicates its magnitude. To combine vectors, link them head to tail and use Pythagoras’ Theorem (or other trigonometric methods) to find their magnitude.

1.4 Graphs:

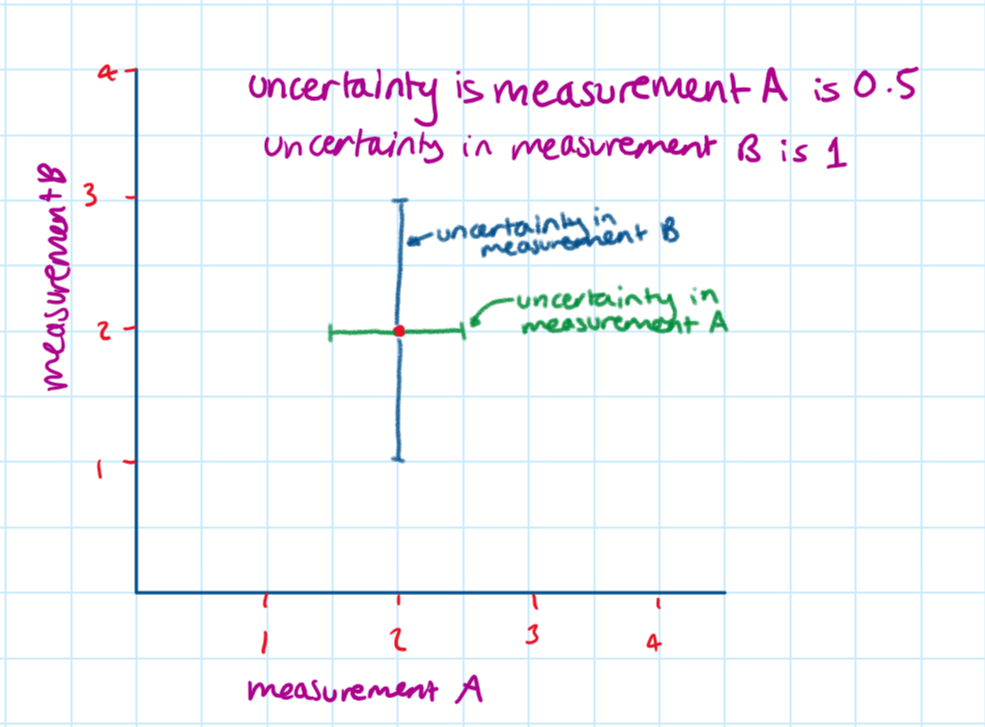
You can draw error bars by adding a vertical and horizontal bar to each point which is the length of the uncertainty in the measurement on that axis.

We draw lines of best-fit by drawing a straight line which attempts to minimise the distance between the points and the line - this means that some points are above and some points are under the best-fit line.

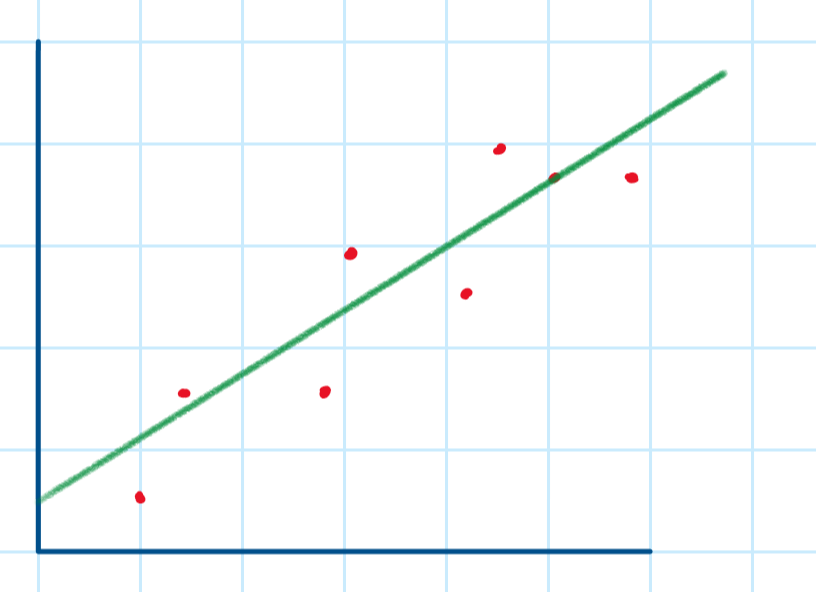
The lines of the minimum and maximum gradient are drawn by connecting a point on the lowest point’s error bar to a point on the top point’s error bar.

We can find the uncertainty in the gradient (line of best fit) by using these values in the formula:

ΔK= (k_max - k_min)/2

where:

• k = gradient

• ΔK = uncertainty in the gradient

Chapter 2: Mechanics

2.1 Kinematics

Important terms:

• distance (d, x, r, y, z) - how far travelled in any direction measured in meters (m)

• speed (v) - how fast travelled in any direction measured in meters per second (ms^-1)

  • formula for speed:distance/time

• instantaneous speed (v) - the speed at a specific distance measured in meters per second (ms^-1)

• average speed (v) - the speed over a total distance measured in meters per second (ms^-1)

• displacement (s) - distance in a specific direction measured in meters (m)

• velocity (v) - speed in a specific direction measured in meters per second (ms^-1)

• acceleration (a) - change in speed over time measured in meters per second squared (ms^-2)

  • formula for acceleration:velocity/time

Vectors are measurements that have magnitude and direction whereas scalars are measurements with only magnitude. Therefore, distance and speed are both scalars and acceleration, velocity and displacement are vectors.

Equations of Uniform Motion (SUVAT):

• there are 4 kinematic equations (known as SUVAT) that can describe any object moving with constant or uniform acceleration.

  • s = displacement

  • u = initial velocity (at t=0)

  • v = final velocity

  • a = acceleration

  • t = time interval

• the four kinematic (SUVAT) equations are

  • v=u+at

  • s=ut+(1/2)at²

  • v²=u²+2as

  • s=((v+u)/2)t

We can make many assumptions about the nature of one or more of the SUVAT components based on the wording of the question:

• if the question says “starts from rest” or does not mention the initial velocity, u and t can be assumed to equal zero

• if the object is at its maximum height, v must equal zero

• if the object is falling (or being thrown upwards) a is equal to g, therefore meaning its value must be 9.81 (or -9.81)

Projectile Motion:

The trajectory of an object undergoing projectile motion consists of two components, a vertical component and a horizontal component. We must evaluate these two components separately.

Key things to remember are:

• the acceleration due to gravity is g and is downwards and constant throughout the motion

• the horizontal velocity V_v is constant and in the direction of the object throughout the motion

• the vertical velocity V changes in direction and magnitude throughout the motion e.g. at the top V_v=0

Graphs:

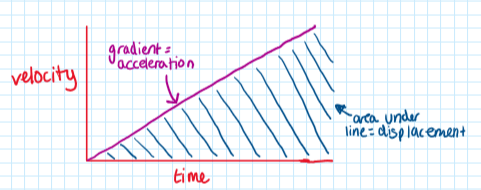
Displacement-time graph:

Velocity-time graph:

2.2 Forces and Motion

Newton’s First Law:

Newton’s first law of motion states:

If the resultant force acting on an object is zero, it is said to be in translational equilibrium. Therefore, the body must either be at rest or moving at a constant velocity.

Newton’s Second Law:

Newton’s second law of motion states:

We can also write this as: F=ma

• F= resultant force (N)

• m = mass (kg)

• a = acceleration (ms^-2)

This means that objects will accelerate if there is a resultant force acting upon them.

Newton’s Third Law:

Newton’s third law of motion states:

Forces arise in pairs, therefore if object A exerts a force on object B, then object B exerts an equal and opposite force on object A. A Newton’s third law force pair must be the same type of force, the same magnitude, opposite in direction and on different objects.

Contact Forces:

A contact force is defined as:

Examples of contact forces include:

• friction - a force that opposes motion and occurs when objects rub against one another

  • static friction occurs when a body is stationary on a surface and is equal to Ff<µsFn

    • Ff = surface frictional force (N)

    • µs = coefficient of static friction (between 0 or 1 but not one of those numbers)

    • Fn = normal reaction force (N)

  • dynamic friction occurs when a body is in motion on a surface and is equal to Ff=µdFn

    • Ff = surface frictional force (N)

    • µd = coefficient of dynamic friction

    • Fn = normal reaction force (N)

• air resistance - a type of friction that occurs when an object moves through air

• tension - a force that pulls two objects connected by a length of something (often string or rope) and occurs when a force is applied to the length

• normal/reaction force - a component of the contact force acting perpendicular to the surface that counteracts the body and occurs when an object is supported by a surface

Non-Contact Forces:

A non-contact force is defined as

Examples of non-contact forces include:

• gravitational force - an attractive force experienced by two objects with mass in a gravitational field

• electrostatic force - a force experienced by charged objects in an electric field which can be attractive or repulsive

• magnetic force - a force experienced between magnetic poles in a magnetic field that can be attractive or repulsive

Hooke’s Law:

Hooke’s Law states that:

This is represented by the equation Fh=-kx

• Fh = elastic restoring force (N)

• k = spring constant (Nm^-1) (the larger this number the stiffer the material)

• x = extension (m)

Stoke’s Law:

Viscous drag is defined as:

It is calculated using Stoke’s Law: Fd=6πηrv

• Fd = viscous drag force (N)

• η = fluid viscosity (Nsm^-2 or Pa s)

• r = radius of the sphere (m)

• v = velocity of the sphere through the fluid (ms^-1)

The size of the force depends on the speed, size and shape of the object.

Archimedes principle:

Buoyancy is experienced by a body partially or immersed in a fluid. The size of the force that produces this (known as upthrust) is equal to the weight of the water displacement.

It is equal to Fb=pVg

• Fb = buoyancy force (N)

• p = density of the fluid (kgm^-3)

• V = volume of the fluid displaced (m³)

• g = gravitational field strength (ms^-2)

Conservation of Linear Momentum:

The momentum of an object is defined as the product of mass and velocity. It is equal to p=mv.

• p = momentum (kgms^-1)

• m = mass (kg)

• v = velocity (ms^-1)

Momentum is a vector quantity, it has both magnitude and direction and therefore can have both a negative and a positive value. The principle of conservation of linear momentum states that:

Impulse and Momentum:

Impulse is equal to the change or momentum of a system: J=Δp=mv-mu

• J = impulse (Ns)

• Δp = change in momentum (kgms^-1)

• m = mass (kg)

• v = final velocity (ms^-1)

• u = initial velocity (ms^-1)

It can also be defined in terms of the average resultant force: J=FΔt

• J = impulse (Ns)

• F = average resultant force (N)

• Δt = time of contact (s)

Force and Momentum:

The resultant force on a body is the rate of change or momentum, defined as: Δp=pf-pi

• Δp = change in momentum (kgms^-1)

• pf = final momentum (kgms^-1)

• pi = initial momentum (kgms^-1)

It can also be expressed as F= Δp/Δt

• F = resultant force (N)

• Δt = change in time (s)

Collisions and Explosions:

In both explosions and collisions momentum is always conserved. However, kinetic energy isn’t always. A collision (or explosion) is either elastic, if the kinetic energy is conserved, or inelastic, if it is not.

Angular Velocity:

The speed of an object going around in a circle remains constant, however its velocity changes. The speed of the object going around is equal to: 2πr/T

• r = radius of the circle (m)

• T = the time period (s)

Its frequency can be determined from the equation: f=1/T

• f = the frequency (Hz)

• T = the time period (s)

The angular speed of a body in circular motion (which is a scalar quantity) is defined as:

We calculate it using the equation: ω= Δθ/Δt

• ω = angular speed (rads^-1)

• θ = angular displacement (rad)

• t = time taken (s)

The linear speed is related to the angular speed by the equation: v=rω

• v = linear speed (ms^-1)

• r = radius of circle (m)

• ω = angular speed (rads^-1)

Centripetal Force:

The centripetal force is defined as:

It can be found using the equation: F=mv²/r

Or by the equation: F=mrω²

• F = centripetal force (N)

• v = linear speed (ms^-1)

• ω = angular speed (rads^-1)

• r = radius of the orbit (m)

• m = mass (kg)

Centripetal Acceleration:

Centripetal acceleration is defined as:

It can be defined using the equation: a=v²/r

Or using the equation: a=ω²r

• a = centripetal acceleration (ms^-2)

• v = linear speed (ms^-1)

• r = radius of the circular orbit (m)

• ω = angular speed (rads^-1)

Work, Energy & Power

Principle of Conservation of Energy:

The principle of conservation of energy states that:

Therefore, the total amount of energy in a closed system (one without outside interference) must be constant

Chapter 3: Thermal physics

3.1 Thermal Concepts

Molecular Theory of Solids, Liquids, and Gasses

• Molecules are held together by intermolecular forces.

• Plasma state is a highly ionized, electrically conductive gas with charged ions and free electrons; it exhibits conductivity in high-temperature environments

Temperature and Absolute Temperature

• Temperatures describe an object's hotness or coldness, determining heat flow direction.

• Heat transfer: higher to lower temperature; termed "heat."

• Thermal equilibrium: objects share the same temperature.

• Kelvin temperature is calculated by adding 273.15 to the Celsius temperature.

• Absolute temperature (Kelvin) is proportional to the average kinetic energy per molecule.

• Absolute zero: 0K or -273°C, particles at zero average kinetic energy.

Internal Energy

• Internal energy: sum of total kinetic and potential energy.

• Kinetic energy is associated with molecular motions.

• Potential energy is linked to intermolecular forces.

Specific Heat Capacity

• Substance-specific heat capacity: heat needed to raise 1kg by 1K.

• Different substances have distinct heat capacities due to varying properties.

• Thermal capacity: Q = cθ (or Q = cΔT) - or the heat to raise the object's temperature by 1K.

  • Heat (Q): The unit of heat is typically measured in joules (J) in the International System of Units (SI).

  • Thermal capacity (c): The unit of thermal capacity is also joules per Kelvin (J/K) in the SI system.

  • Temperature change (θ or ΔT): The unit of temperature change is Kelvin (K) in the SI system.

Phase Change

• Solid to Liquid (Melting)

  • Kinetic energy is unchanged; potential energy increases.

• Liquid to Solid (Freezing)

  • Kinetic energy is unchanged; potential energy decreases.

• Liquid to Gas (Boiling)

  • Kinetic energy is unchanged; potential energy increases.

• Gas to Liquid (Condensation)

  • Kinetic energy is unchanged; potential energy decreases.

• During phase change, temperature and kinetic energy remain constant, while potential energy changes.

Specific Latent Heat

• Specific latent heat: heat needed for phase change without temperature change.

• Latent Heat of Fusion

  • Heat to change 1kg from solid to liquid.

• Latent Heat of Vaporization

  • Heat to change 1kg from liquid to gas.

3.2 Modeling a Gas

Pressure

• Pressure: normal force per unit area.

• Equation: P = F/A.

  • Pressure (P): The unit of pressure is measured in pascals (Pa) in the International System of Units (SI). One pascal is equivalent to one newton per square meter (N/m²).

  • Force (F): The unit of force is measured in newtons (N) in the SI system.

  • Area (A): The unit of area is measured in square meters (m²) in the SI system.

Equation of State for an Ideal Gas

• Ideal gas equation: PV = nRT, where R = 8.31 (J/mol/K).

  • Pressure (P): The unit of pressure is typically measured in pascals (Pa) in the International System of Units (SI).

  • Volume (V): The unit of volume is typically measured in cubic meters (m³) in the SI system.

  • Amount of substance (n): The unit of amount of substance is measured in moles (mol).

  • Gas constant (R): The unit of the gas constant depends on the units used for pressure, volume, and temperature in the equation. In this case, R = 8.31 J/mol/K, where the unit of R is joules per mole per Kelvin (J/mol/K).

  • Temperature (T): The unit of temperature is measured in Kelvin (K) in the SI system.

Kinetic Model of an Ideal Gas

• Assumptions:

  • Perfectly elastic molecule collisions.

  • Identical spherical molecules.

  • Negligible molecular volume compared to gas volume.

  • No interaction except during collisions.

• Implications:

  • Absolute temperature is directly proportional to average kinetic energy and speed.

Mole, Molar Mass, and Avogadro Constant

• Mole:

  • Unit of quantity, like a “dozen.”

  • 1 mole = 6.022*10²³ atoms or molecules (Avogadro’s constant).

• Molar Mass:

  • Mass of 1 mole of any element or compound.

• Avogadro’s Constant:

  • 6.022*10²³.

Differences Between Real and Ideal Gasses

• Real gasses deviate from ideal assumptions.

• Intermolecular forces exist in real gasses.

• Molecular volume is not negligible.

• Real gasses may resemble ideal gasses under high temperatures and low pressure.

Chapter 4: Oscillations and waves

4.1 Oscillations

• Periodic Motion:

  • Motion that repeats itself after equal intervals of time. 

    • Examples include the motion of a loaded spring, an object moving in a circle, and a simple pendulum.

• Terms Related to Periodic Motion:

  • Amplitude (A): Maximum displacement from the equilibrium position.

  • Time period (T): Time taken for a complete oscillation.

  • Frequency (f): Number of oscillations per unit time. (f = 1/T)

  • Angular frequency (𝓌): Equivalent of frequency. (𝓌 = 2(π)f)

  • Phase (θ): If the motion starts away from equilibrium, it leads or lags by θ.

  • Isochronous oscillations: Maintain a constant time period regardless of amplitude changes.

• Simple Harmonic Motion (SHM):

  • A type of periodic motion where the restoring force is proportional to the negative displacement from the equilibrium position. 

    • Examples include a spring-loaded with a mass and a simple pendulum with a small amplitude.

  • Equation defining SHM: a - kx where a is accelerated, k is a constant, and x is displacement.

    • Units of constant k: 

      • K = - a/x, so the unit of k is m x s^-2 / m = s^-2.

    • Difference in oscillations of two systems S1 and S2.

      • If S1 has frequency f, S2 with 4k frequency has a frequency of √4f = 2f

• Describing Simple Harmonic Motion:

  • Equation for SHM: x  = Asin(2πft + θ) = Asin(wt + θ), where θ is π/2

• Velocity (v):

  • v = (dx)/(dt) = 𝓌Acos(𝓌t + θ)

• Acceleration(a):

  • a = (dv)/(dt) = -𝓌^2(A)(sin(𝓌t+θ))

• Phase difference between displacement-time graphs:

  • About 25 seconds

  • 0.79 radians

• Circular Motion and SHM: 

  • The projection of an object in circular motion on a diameter follows simple harmonic motion.

• Energy Changes in Simple Harmonic Motion:

  • Kinetic energy: KE= ½(m𝓌^2A^2)

    • Total energy remains constant in the absence of dissipative forces.

• Waves and their types:

  • Mechanical waves: require a material medium to travel

  • Electromagnetic waves: can travel through a vacuum.

• Describing Waves:

  • Wavefront: A surface perpendicular to the direction of wave travel.

  • Amplitude (A): Maximum displacement from equilibrium.

  • Wavelength (⅄): Shortest distance between two points in phase on a wave.

  • Period (T): Time for a complete wavelength to pass a fixed point.

  • Frequency (f): Number of wavelengths passing through a fixed point per unit time.

    • f = 1/T

4.2 Traveling waves

• Transverse waves: Direction of vibration perpendicular to the direction of propagation.

• Longitudinal waves: Direction of vibration parallel to the direction of propagation. 

• Wave Equation:

  • The velocity of a wave (c) is given by c = f⅄

• Electromagnetic waves:

  • Travel with varying electric and magnetic fields at 3 x 10^8 m/s in a vacuum.

4.3 Wave characteristics

• Intensity of Waves:

  • Intensity (I) is power received per unit area. I = (P)/(4πr^2) and is proportional to the square of amplitude (A^2).

  • Example:

    • Intensity at 120m from source: 3 x 10^-6 W/m^2.

• Principle of Superposition:

  • When two waves meet, the total displacement is the vector sum of their individual displacements.

• Polarization:

  • Restriction of oscillation direction to a plane perpendicular to the direction of propagation. Result: Plane-polarized light.

• Malus’s Law:

  • Intensity (I) transmitted by an analyzer is proportional to cos^2(θ) where θ is the angle between the polarizer and the analyzer.

4.4 Wave Behaviour

• Laws Of Reflection And Refraction:

  • Incident, reflected, and refracted rays, and normal lie on the same plane.

  • The angle of incidence equals the angle of reflection.

  • (sinθ1)/(sinθ2) = 1/n (Snell’s Law)

• Reversibility of Light:

  • (sinθ1)/(sinθ2) = 1/n_2 for light going from medium 1 to medium 2, and (sinθ1)/(sinθ2) = 1/n_1 for light traveling in the opposite direction.

• Critical Angle And Total Internal Reflection:

  • The angle of incidence for which the angle of refraction reaches the right angle is the critical angle. 

  • Total internal reflection occurs when the angle of incidence is greater than the critical angle.

• Double-Slit Interference:

  • Two coherent sources create interference patterns. Constructive interference occurs at nλ and is destructive at (n + ½)λ.

  • Example:

    • The path difference at point P is 7λ. The nature of the fringe at P is bright, and there are 7 dark fringes between O and P.

• Diffraction:

  • Wave passed through a narrow gap forms bright and dark fringes. Angular position of minima given by θ = (nλ/a).

  • Example:

    • Path difference at point P is 7λ. 

    • The nature of fringe at P is bright, and there are 7 dark fringes between O and P.

• Interference With Multiple Slits:

  • More slits result in sharper and more intense maxima and minima.

• Dispersion:

  • Different wavelengths of light refract at different angles. White light disperses into its constituent wavelengths.

• Resolution:

  • Rayleigh's criterion states two points are just resolved if the central maximum of the first point falls on the first minimum of the second point.

• Diffraction Grating:

  • For a grating with N slits, R = λ/change in λ = mN

• Reflection Of Light Off Thin Films:

  • Reflected light undergoes a phase change of 180∘ if reflected off a denser medium. 

  • A thin film of thickness t, refractive index n, and incident wavelength λ exhibits interference.

• Doppler Effect In Light:

  • The change in frequency of the light wave is (v/c)(f_0).

• Water Waves:

  • Follow laws similar to light. Exhibit reflection, refraction, interference, and diffraction.

• Wave Propagation:

  • Wavefront consists of infinite new disturbance centers. 

  • Successive wavefronts result from wavelets from these disturbances.

• Reflection Of Water Wave:

  • When a wave hits a barrier, it behaves as if a similar wave is coming from the barrier in the opposite direction.

• Doppler Effect In Sound:

  • The frequency of a moving source changes for an observer at rest or moving toward/away from the source.

4.5 Standing waves

• Boundary Conditions:

  • Reflected off a fixed boundary suffers a phase change of 180∘. 

  • No change in the phase of a free boundary.

• Standing Waves:

  • Formed when two waves of equal amplitude and frequency traveling in opposite directions are superimposed. 

  • Positions of crests and troughs do not change with time.

• Nodes and Antinodes:

  • Nodes are points with zero displacement, antinodes are points with maximum displacement.

• Harmonics On A String:

  • The string is tied at one end and connected to a vibration generator at the other. 

    • Harmonics formed with increasing loops at n times the frequency of the first harmonic.

• Displacement of string at different times:

  • Quarter of a cycle: t = 1/4f

  • Half of a cycle: t = 1/2f

• Frequency of vibration of the spring:

  • Wavelength 2L, wave velocity 240 m/s, frequency 120 Hz.

• Harmonics In A Pipe:

  • Harmonics formed with one end open or both ends open. Nodes form at closed ends and antinodes at open ends.

• Explanation regarding refraction of light: 

  • The speed of light is faster in a vacuum than in water, bending away from normal.

• The critical angle for total internal reflection:

  • sinፀ_c = 1/n

    • where n is the relative refractive index of denser material with respect to rarer material.

• Frequency of the first harmonic if both ends are open: 

  • Twice the frequency of the first harmonic when one end is closed

Chapter 5: Electricity and magnetism

5.1 Electric Fields

Electric Charge:

• Electric charge comes in two forms: positive and negative.

• Like charges repel each other, while opposite charges attract.

• An object with equal positive and negative charges is electrically neutral.

• The unit of electric charge is the coulomb (C).

• The charge of one electron is approximately 1.6 × 10^-19 C.

• Electric charge is conserved, meaning the total charge remains constant even as charges move between objects.

• Conductors allow the flow of electric charge due to the presence of free electrons (e.g., metals, graphite, and humans).

• Insulators do not permit the passage of electric charge (e.g., wood, glass, and plastic).

Electric Field:

• Electric fields can be visualized as electric field lines.

• The direction of the field at a point corresponds to the direction of the field line passing through it, typically from the positive pole to the negative pole.

• The density of field lines around a point represents the field's magnitude.

• In a uniform electric field, field lines are straight, parallel, and evenly spaced.

• Non-uniform electric fields result in curved field lines near edges.

• Electric field strength (E) measures the force per unit charge experienced by a positive test charge placed in the field.

• Coulomb's law de

• scribes the relationship between electric field strength, force, charges, and distance.

5.2 Heating Effect of Electric Currents

Circuit Diagrams:

• An electric circuit is a closed loop of interconnected electrical components.

Resistors:

• Resistors introduce specific resistance in a circuit.

• Variable resistors have adjustable resistance.

• Resistors can be connected in series or in parallel.

Voltmeters:

• Voltmeters measure the potential difference (voltage) between two points.

• They are connected in parallel with the components being measured.

• Ideal voltmeters have infinite resistance.

Ammeters:

• Ammeters measure current flow.

• They are connected in series at the measurement point.

• Ideal ammeters have zero resistance.

Kirchhoff's Circuit Laws:

• Kirchhoff's junction rule enforces the conservation of charge flow.

• Kirchhoff's loop rule ensures the conservation of electric potential energy per charge.

Resistance and Ohm's Law:

• Resistance (R) opposes electric current and is the ratio of potential difference (V) to current (I).

• Ohm's law states that current is proportional to voltage, with a constant resistance (Ohmic conductor).

• Non-Ohmic conductors exhibit non-linear graphs.

Resistivity:

• Resistance depends on the object's length (L), cross-sectional area (A), and resistivity.

• Resistivity is a material-specific constant.

Power Dissipation:

• Power (P) dissipated in a resistor is calculated as P = IV.

• Electrical energy is converted into heat or other forms of energy.

5.3 Electric Cells

Cells:

• A cell is an energy source in a circuit, creating an electric potential difference.

• A battery consists of connected cells.

• Internal resistance affects the EMF  (electromotive force) of a cell.

Secondary Cells:

• Secondary cells, or rechargeable batteries, can be recharged by reversing the current flow.

Terminal Potential Difference:

• The potential difference at a cell's terminals is less than its EMF due to internal resistance.

Electromotive Force (emf):

• The emf is the energy supplied per unit charge by a cell.

• It is measured in volts (V).

5.4 Magnetic Effects of Electric Currents

Magnetic Fields:

• Magnetic fields result from magnets or moving charges.

• Magnets or electric currents experience forces in magnetic fields like electric charges in electric fields.

• Magnetic field strength is measured in tesla (T).

Magnetic Field Patterns:

• Magnetic fields are represented using magnetic field lines.

• The direction and density of field lines indicate the field's strength and direction.

• Magnetic fields can be viewed in 3D with dots (out of the page) and crosses (into the page)

Magnetic Force:

• The force on a current-carrying wire in a magnetic field is calculated using the formula F = BIL, where B is the magnetic field, I is the current, and L is the length of the wire.

• The force acts perpendicularly to both the wire and the field.

• The magnetic force on a moving charge is given by F = qvB, where q is the charge, v is the velocity, and B is the magnetic field.

• The direction of conventional current is opposite to electron flow.

• Magnetic forces cause the charge to follow a circular path, acting as a centripetal force.

• No work is done on the charge by the magnetic field.

Chapter 6: Circular Motion and Gravitation

6.1 Circular Motion

Rotational Motion

In addition to translational motion, objects that are not points, and systems of objects, can rotate. We shall consider only rigid objects (rigid bodies) which have a fixed shape. For now, the rotation is around a single line in space called the axis of rotation.

Polar Coordinates

Every point in the object moves in a circle. Point P has coordinates x,y,z and is a distance r from the axis. At time t the position vector makes an angle θ with the x axis.

Because the motion is circular the coordinates x and y are not very useful. The more useful coordinates are the polar coordinates r and θ.

Angular Velocity

• At time t_1 the angle is θ1; at time t _2 the angle is θ2.

The average angular velocity ω is defined to be: 

ω¯= change in angle/change in time = (θ2−θ1)/(t 2−t 1) = Δθ/Δ t

The units of ω are radians/s (rad/s). By convention, if ω is positive the rotation is counterclockwise (CCW), if it is negative the rotation is clockwise (CW).

• When the time interval approaches zero the average angular velocity becomes the instantaneous angular velocity ω.

Angular Acceleration

At time t_1 the angular velocity is ω1; at time t_2, the angular velocity is ω2.

The average angular acceleration α is defined to be

• α¯= change in angular velocity / change in time = (ω2−ω1)/ (t 2−t 1) = Δ ω / Δt

The units of α are rad/s^2.

When the time interval approaches zero the average angular acceleration becomes the instantaneous angular acceleration α.Any point in the object still has a linear (tangential) velocity, speed and acceleration.

• The velocity vector always points along the tangent to the circle.

If the distance of the point is r from the axis then the linear speed is

• v= r × ω

In a rigid object the tangential speed increases with distance from the axis of rotation.

• The circumference of the circle grows but the period does not.

An object moving in a circle is accelerating. The acceleration is related to the angular acceleration and angular velocity. The general relation is complicated because in general there are two components of the acceleration.

• One points towards the center and is called the centripetal acceleration a_C

• The centripetal acceleration causes the velocity to change direction only.

• The other points in the same direction as the velocity (or opposite it) and is called the tangential acceleration, a_tan.

• The tangential acceleration changes the size of the velocity (speed) only.

They are related to ω and α by the equations.

• a_C=r×ω^2 = v^2/r

• a_tan =r×α

In the special case where a_tan is zero, the acceleration points towards the center of the circle, and the object’s speed is constant.

• This kind of motion is called uniform circular motion.

• In general the acceleration points in a non-central direction. 

  • This kind of motion is called non-uniform circular motion.

Centripetal Force

• The centripetal acceleration occurs due to the application of a force called the centripetal force.

  • Typically the force is a tension in a string, gravity, or a normal force, it is not some new force in the problem.

• Since we know the centripetal acceleration, the force must be:

  • ∑ _radial components F= FC=maC= mv^2 / r = m × r × ω^2

• The sum is over the radial components of the applied forces.

  • If an applied force has no radial component then it doesn't contribute.

  • If the component points towards the axis of rotation it is positive, away from the axis of rotation it is negative.

A rider on a Ferris wheel moves in a vertical cir]cle of radius r at constant tangential speed v.

• How does the normal force that the seat exerts on the rider change compared to the rider’s weight at the top and bottom of the wheel?

  • Another common instance of circular motion occurs when a car rounds a curved road.

• The centripetal force – the force that causes the car to follow the curved road – is friction and/or the normal force if the road is banked.

  • If the wheels are not skidding then the point on the tire in contact with the ground is not moving plus the friction is perpendicular to the motion so the appropriate friction to use is static friction, not kinetic or rolling.

Centrifugal Force

In the frame of reference of an object moving in a circle, there is a force pushing on the object in the outward direction. This force is called the centrifugal force.

• Centrifugal force, often referred to as a "fictitious" or "pseudo" force, is a concept in physics that arises in a rotating or non-inertial frame of reference. It appears to act outward from the center of rotation, opposing the centripetal force, which is directed toward the center of rotation to keep an object in circular motion. Here are some key notes about centrifugal force:

  • Fictitious Force:

    • Centrifugal force is not a real force like gravity or electromagnetism. 

      • It is a perceived force that appears to push objects away from the centre of rotation when you are observing the motion from a rotating frame of reference.

    • It is a consequence of inertia and the tendency of objects to move in a straight line, rather than following a curved path.

  • Centripetal Force:

    • In a rotating system, such as a spinning object or a car moving in a circular path, there must be a centripetal force acting on the object to keep it in its circular path. 

      • This centripetal force is directed toward the centre of rotation.

    • The centrifugal force is often introduced as an apparent force that seems to counteract the centripetal force. 

      • In reality, the object is simply moving in a straight line, but because of its inertia, it appears to be pushed outward.

  • Magnitude of Centrifugal Force:

    • The magnitude of the centrifugal force is directly proportional to the square of the angular velocity (rate of rotation) of the system and the distance of the object from the center of rotation.

    • Mathematically, the centrifugal force can be calculated as F_c = m (ω^2) r, where F_c is the centrifugal force, m is the mass of the object, ω is the angular velocity, and r is the distance from the center of rotation.

• Examples:

  • Common examples of centrifugal force include 

    • the sensation of being pushed outward when turning a curve in a car

    • the clothes sticking to the outer drum of a washing machine during the spin cycle

    • objects moving away from the center of a merry-go-round when it spins.

• Non-Inertial Frames of Reference:

  • Centrifugal force is most often discussed in the context of non-inertial frames of reference. 

    • In an inertial frame (one at rest or moving at a constant velocity), the concept of centrifugal force is not necessary, as objects follow a straight-line path unless acted upon by a real force.

• Understanding Circular Motion:

  • It is important to recognize that centrifugal force is a useful concept for understanding motion from a rotating frame of reference, but it does not represent a real physical force. 

  • The actual force responsible for keeping an object in circular motion is the centripetal force.

6.2 Newton’s Law of Gravitation

Newtonian Synthesis

• Until Isaac Newton, it was thought that the ‘physics’ of things outside the Earth – the celestial - was different from that of things on the Earth – the terrestrial. Newton rejected this division and applied the same physical laws to both.

• The force that causes an apple to accelerate as it falls is the same force that holds the Moon to the Earth.

• This unification of the physics governing the celestial and terrestrial is known as Newtonian Synthesis. 

  • Newtonian Synthesis had such a profound effect that one of its consequences was the American Revolution.

• Newton tried to find one ‘Law of Gravity’ to explain the motion of objects here on Earth and the motion of the planets. He was aided by 3 facts:

• He knew the force of gravity upon objects here on Earth. If ‘1’ is the object and ‘2’ is the Earth then the weight of object 1 due to object 2 is

  • F_on1from2 = m_1×g_2 where g2 is the acceleration due to the gravity from object 2)

• His 3rd Law tells him that this must also be the force on Earth from the object

• F_on2from1=m_2×g_1 where g1 is the acceleration due to the gravity of the object.

• The motion of the planets around the Sun is described by three laws found sometime earlier by Kepler.

Kepler’s Laws

Many decades before Newton, Johannes Kepler discovered three laws of planetary motion based on observation. 

• The path of each planet about the Sun is an ellipse with the Sun at one focus.

• An imaginary line drawn from each planet to the Sun sweeps out equal areas in equal times.

• The square of a planet’s orbital period is proportional to the cube of its mean distance from the Sun.

• Since the Sun is at a focus, the mean distance from the Sun is the same as the semimajor axis.

• T^2∝s^3

• The ratio of s3 / T2 is the same for all planets.

  • s_1^3 / T_1^2 = s_2^3 / T_2^2

Newton’s Law of Universal Gravitation

• The first two ‘facts’ tell Newton the force of gravity between two objects must be proportional to the product of their masses.

  • g1 must be proportional to m1, g2 must be proportional to m2

• What he doesn’t know is if it depends upon anything else. Newton tried an idea that others had suggested: the force of gravity decreases as the square of the distance between the two objects.

  • This is called an inverse square law.

• With this assumption and his three Laws of Motion, he is able to derive Kepler’s three laws.

  • Later he shows that any other scaling with distance does not give Kepler’s three laws.

• Newton’s Law of Universal Gravitation can be stated as:

Every particle in the universe attracts every other particle with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between them. This force acts along a line joining the two particles

• In mathematical form:

• G is a constant called Newton's Gravitational Constant, or Big G, and has a  value of G = 6.67 x 10^-11 N m^2 / kg^2

• Gravity is quite different from the other forces we have met: it acts even though two objects are not in contact.

  • This is sometimes called Action At A Distance.

  • Something must happen to change the space between the two objects.

Gravitational Fields

• "Gravitational field notes" likely refer to observations, measurements, or data collected regarding the gravitational field in a particular location or region. 

  • The gravitational field is a region in which an object with mass experiences a force due to gravity. Here are some key points that might be included in such notes:

• Location and Coordinates:

  • The specific location where the observations or measurements were taken, including latitude, longitude, and elevation.

• Gravitational Field Strength (Intensity):

  • Measurements of the strength of the gravitational field. 

  • This is typically expressed in units like newtons per kilogram (N/kg) or as the acceleration due to gravity (9.81 m/s² on the surface of the Earth).

• Variations in Field Strength:

  • Notes on any variations or anomalies in the gravitational field strength within the area of study. 

  • These could be due to geological features, underground structures, or other factors.

• Instrumentation and Methodology:

  • Details about the equipment or instruments used to measure the gravitational field. 

  • This might include gravimeters, accelerometers, or other specialized devices.

• Temporal Variations:

  • Any observations or measurements related to how the gravitational field strength changes over time. 

  • This could be due to tides, seasonal variations, or other factors.

• Comparisons with Known Data:

  • Comparisons of the collected data with existing records or models of the gravitational field for that region. 

  • This helps to validate the measurements and identify any discrepancies.

• Potential Applications:

  • Speculation or discussion on how the observed gravitational field might impact various applications. 

    • For example, it could be relevant in geophysics, navigation, or even space exploration.

• Other Pertinent Observations:

  • Any additional relevant observations that might affect or be affected by the local gravitational field. 

    • This could include phenomena like subsidence, seismic activity, or magnetic anomalies.

• These field notes would be valuable for researchers, geophysicists, engineers, or anyone working on projects where an understanding of the local gravitational field is important. 

• They serve as a record of the conditions and data collected, which can be referred to for analysis and comparison in the future.

  • If the mass is m then the force of gravity on that object is mg.

  • g = F / m, or Gravitational Field Strength (g) is equal to Gravitational Force (F) over Mass of the Object (m)

Force fields are often represented by field lines.

Chapter 7: Atomic and Nuclear Physics

7.1 Discrete Energy and Radioactivity

Discrete energy:

Emission spectrum represents different possible wavelengths of light emitted by an atom.

• When gas at low pressure is subjected to a strong electric field, it emits light at discrete wavelengths.

• The emission spectrum (e.g., hydrogen, helium, mercury) comprises lines at specific wavelengths, representing photon emissions during electron transitions between energy levels.

• Emission spectrum: Series of bright lines representing the wavelengths that can be emitted by an atom.

• From the excited state, the electron will immediately (within nanoseconds) make a transition down to one of the available lower energy states.This process is called relaxation.

• , h is planck's constant, is the wavelength emitted during relaxation and c is the speed of light, whereas E is the energy released.

• This means that the light that is transmitted through the gas will be missing the photons that have been absorbed.This gives rise to absorption spectra

• Radioactivity: Spontaneous emission of particles and energy from an unstable nucleus.

• Discovered by Henri Becquerel, Marie Skłodowska-Curie (1867–1934), and Pierre Curie (1859–1906).

  • Alpha particles: Helium nucleus emitted during alpha decay.

  • Beta particles: Electrons or positrons emitted during beta decay.

  • Gamma rays: High-frequency electromagnetic radiation from nucleus transitions.

Nuclear transmutation: Transformation of one element to another through nuclear reactions, such as alpha particle collision with nitrogen to produce oxygen and a proton.

Nuclear fission:

Splitting of a heavy nucleus into lighter nuclei, with the release of energy.

Example: Absorption of a neutron by uranium-235, resulting in uranium-236, which then fissions into krypton, barium, and more neutrons.

Chain reaction: Self-sustaining fission process due to released neutrons inducing further reactions.

Critical mass: Minimum mass of fissile material needed to maintain a chain reaction.

Nuclear fusion:

Joining of light nuclei to form a heavier nucleus, releasing energy.

Occurs in stars and hydrogen bombs, but controlled fusion for energy production is still a challenge.

• Nuclear structure: Constituents of a nucleus (protons and neutrons) and their organization.

  • Atomic (proton) number (Z): Number of protons in a nucleus.

  • Mass (nucleon) number (A): Sum of protons and neutrons in the nucleus.

  • Neutrons (N): Calculated as N = A - Z.

Isotopes: Atoms with the same number of protons but different numbers of neutrons. Physical properties vary, but chemical properties are identical due to the same number of electrons.

Radioactive isotopes: Exhibit spontaneous radioactive decay.

Radioactive decay:

Unstable nuclei emit particles and energy spontaneously.

Types of decay: alpha (α), beta (β), and gamma (γ) radiation.

Alpha decay: Emission of an alpha particle (helium nucleus).

Beta decay: Neutron transforms into a proton emitting an electron (beta-minus decay) or proton transforms into a neutron emitting a positron (beta-plus decay).

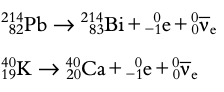
Gamma decay: Emission of a gamma ray, no change in the nucleus's atomic number or mass number.

Half-Life & Probability:

Half-life (t_1/2): The time required for half the quantity of a radioactive substance to undergo decay. A measure of the stability of a radioactive isotope; shorter half-life indicates a more unstable isotope. Determines the rate at which a sample loses its radioactivity.

Exponential decay: The number of undecayed nuclei decreases exponentially over time.

Probability in decay:

Each nucleus has a constant probability of decaying in a given time interval, independent of time.

After one half-life, the probability that a nucleus has not decayed is 50%.

Multiple half-lives follow a predictable pattern: after n half-lives, the fraction remaining is

Decay Series

Radioactive decay series: A sequence of decay events from a parent radionuclide to stable daughter isotopes.

Example: The decay series of uranium-238 to lead-206 involves multiple alpha and beta decays.

Each step in the series has its own characteristic half-life and decay mode.

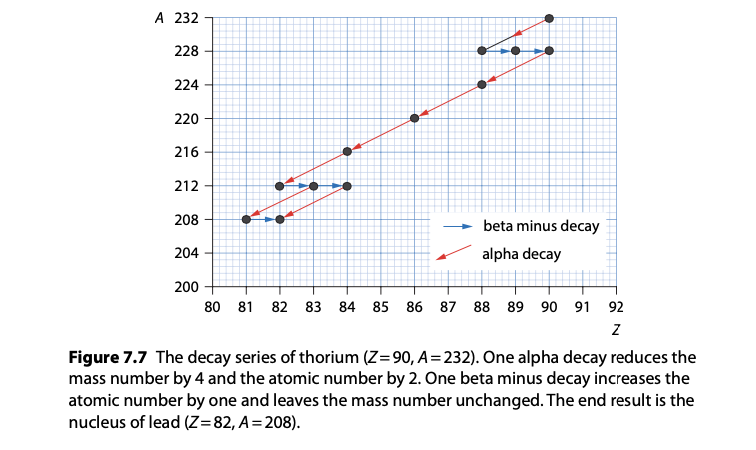
The Law of Radioactive Decay

Radioactive decay law: States that the activity (rate of decay) of a radioactive sample is proportional to the number of undecayed nuclei present at any time.

Mathematically expressed as

, where N is the amount of undecayed nuclei.

7.2 Nuclear Reactions

Transmutation and energy release:

Unified atomic mass unit (u): A standard unit of mass that quantifies mass on an atomic or molecular scale.

1 u is defined as one twelfth the mass of a carbon-12 atom, approximately

1.660539×10^-27 kilograms.

Mass Defect and Binding Energy

Mass defect (Δ): The difference between the mass of the completely separated nucleons and the mass of the nucleus.

Occurs because mass is converted into binding energy when the nucleus forms.

Formula:

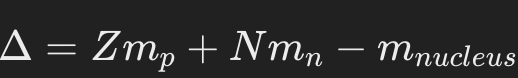
Where is Z is the number of protons, N is the number of neutrons and and is the mass of the proton and mass of the neutron respectively, whereas is the actual mass of the nucleus.

Binding energy: The energy required to disassemble a nucleus into its individual protons and neutrons.

Calculated using Einstein's equation

m is mass defect often given as a lower case delta, and c is the speed of light.

The Binding Energy Curve:

The binding energy per nucleon varies with the nucleon number and has a peak at iron-56, indicating the greatest stability.

Light nuclei (up to iron) gain stability through fusion, while heavy nuclei (beyond iron) gain stability through fission.

Energy Released in Decay

Nuclear fission: A heavy nucleus splits into two smaller nuclei, releasing a large amount of energy.

Example: Uranium-235 undergo fission after capturing a neutron.

Energy released is due to the conversion of mass defect into energy, typically measured in mega-electron volts (MeV).

Nuclear fusion: Lighter nuclei combine to form a heavier nucleus, releasing energy.

Example: Fusion of deuterium and tritium to form helium-4.

Requires high temperatures and pressures to overcome electrostatic repulsion, with the sun being a natural fusion reactor.

7.3 The Structure of Matter

Particle physics:

Investigates fundamental building blocks of matter (quarks and leptons) and their interactions.

Rutherford experiment: Revealed the nucleus and led to the planetary model of the atom.

Fundamental particles:

Quarks: Six types ('flavors') with different properties, combining to form particles like protons and neutrons.

Leptons: Include electrons, neutrinos, and their anti-particles, not subject to the strong interaction.

Exchange particles: Mediate fundamental forces (e.g., photons for electromagnetic force).

Nuclear Forces and Particles:

Strong nuclear force: Binds quarks within protons and neutrons, and these nucleons within the nucleus.

Alpha, beta, and gamma decay: Processes by which unstable nuclei release particles and energy.

The Higgs boson: Particle associated with the Higgs field, which gives mass to other particles in the Standard Model.

Exchange Particles and Fundamental Forces:

Electromagnetic interactions: Mediated by photons.

Weak interactions: Involve W and Z bosons, responsible for processes like beta decay.

Strong interactions: Governed by gluons, binding quarks together within nucleons.

Gravitational interactions: Attributed to gravitons, though not yet experimentally confirmed.

Conservation Laws in Particle Physics

Baryon number: Conserved in nuclear reactions; associated with quarks and baryons.

Lepton number: Conserved for electrons, muons, and their respective neutrinos.

Strangeness: Quantum number conserved in strong interactions, may change in weak interactions.

Electric charge: Conserved in all types of interactions.

Feynman Diagrams:-

Visual representations: Depict particle interactions, with particles as lines and interactions as vertices.

Interaction vertices: Show the exchange of force carriers like photons and W/Z bosons.

Important for calculations: Simplify understanding of complex interactions in quantum field theory.

Exam Tips

• Be prepared to apply knowledge of discrete energy levels and transitions to solve problems.

• Remember to convert eV to joules for energy-related calculations.

• Understand the significance of the binding energy curve and its implications for nuclear stability.

• Be familiar with Feynman diagrams to represent particle interactions and decays.

Chapter 8: Energy Production

8.1 Energy Sources

• Specific Energy and Energy Density of Fuel Sources

  • Specific energy and energy density are vital for quantifying the energy released during combustion.

  • Specific energy: energy per unit mass (energy/mass).

  • Energy density: energy per unit volume (energy/volume).

  • Sankey Diagrams and Energy Degradation

  • Cyclical processes are needed for continuous conversion of thermal energy to work.

  • Some energy is lost to the surroundings, termed degraded energy.

  • Sankey diagrams visually represent energy flows.

8.2 Thermal Energy Transfer

• Conduction, Convection, and Thermal Radiation

  • Conduction and convection require a medium; radiation can transfer through a vacuum.

• Black-Body Radiation

  • A black body absorbs all incident electromagnetic radiation.

  • Black-body radiation follows the Stefan-Boltzmann law.

• Albedo and Emissivity

  • Albedo

    • Measures the ratio of total scattered (reflected) radiation to total incident radiation.

    • Influenced by season, latitude, and terrain.

  • Emissivity

    • Objects radiate a fraction compared to a black body.

    • Emissivity = power per unit area radiated by the object / power per unit area radiated by a black body at the same temperature.

• The Solar Constant

  • Amount of energy falling on 1m^2 of Earth's atmosphere per second.

  • Solar constant is approximately 1366 W/m^2.

• The Greenhouse Effect

  • Greenhouse Gasses

    • Absorb infrared radiation due to natural frequencies.

  • Mechanism

    • Incoming solar radiation takes the form of ultraviolet and visible radiation.

    • Greenhouse gasses trap infrared radiation, leading to the greenhouse effect.

  • Chain Reaction

    • Global warming reduces ice/snow cover, affecting albedo.

    • Carbon dioxide solubility in the sea decreases, increasing atmospheric carbon dioxide.

  • Effects

    • Rising mean sea levels, extreme weather events.

• Energy Balance in the Earth Surface–Atmosphere System

  • Describes how incoming solar energy is used and returned to space.

  • Balanced energy flow maintains a constant Earth temperature.

Chapter 9: Wave Phenomena

9.1 Introduction to Waves

• It transfers energy.

• Usually involves a periodic, repetitive movement.

• Does not result in a net movement of the medium or particles in the medium (mechanical wave).

• There are some basic descriptors of a wave. 

  • Wavelength is the distance between two successive identical parts of the wave. 

  • Amplitude is the maximum displacement from the neutral position. 

    • This represents the energy of the wave. Greater amplitude carries greater energy. 

  • Displacement is the position of a particular point in the medium as it moves as the wave passes. 

    • Maximum displacement is the amplitude of the wave

• Frequency (ƒ) is the number of repetitions per second in Hz, and Period (T) is the time for one wavelength to pass a point.

• The velocity (v) of the wave is the speed at which a specific part of the wave passes a point. The speed of a light wave is c.

9.2 Types of Waves

• Transverse Waves

  • Waves in which the medium moves at right angles to the direction of the wave.

  • The high point of a transverse wave is a crest. The low part is a trough.

  • Examples of transverse waves:

    • Water waves (ripples of gravity waves, not sound through water)

    • Light waves

    • S-wave earthquake waves

    • Stringed instruments

    • Torsion wave

• Longitudinal Waves:

  • A longitudinal wave has the movement of the particles in the medium in the same dimension as the direction of movement of the wave.

  • Parts of longitudinal waves:

    • Compression: where the particles are close together.

    • Rarefaction: where the particles are spread apart.

  • Examples of longitudinal waves:

    • Sound waves

    • P-type earthquake waves

    • Compression wave

Mechanical waves:

• A wave which needs a medium to propagate itself. 

• Sound waves, waves in a slinky, and water waves are all examples of this.

Matter Waves:

• Any moving object can be described as a wave. 

• When a stone is dropped into a pond, the water is disturbed from its equilibrium position as the wave passes; it returns to its equilibrium position after the wave has passed.

Electromagnetic Waves:

• These waves are disturbance that does not need any object medium for propagation and can easily travel through the vacuum. 

• They are produced due to various magnetic and electric fields. 

• The periodic changes that take place in magnetic and electric fields and therefore known as electromagnetic waves.

9.3 Properties of Waves

• The prime properties of waves are as follows:

  • Amplitude – Wave is an energy transport phenomenon. 

    • Amplitude is the height of the wave, usually measured in metres. 

    • It is directly related to the amount of energy carried by a wave.

  • Wavelength – The distance between identical points in the adjacent cycles of crests of a wave is called a wavelength. 

    • It is also measured in metres.

  • Period – The period of a wave is the time for a particle on a medium to make one complete vibrational cycle. 

    • As the period is time, hence is measured in units of time such as seconds or minutes.

  • Frequency – The frequency of a wave is the number of waves passing a point in a certain time. 

    • The unit of frequency is hertz (Hz) which is equal to one wave per second.

  • The period is the reciprocal of the frequency and vice versa.

  • Speed – The speed of an object means how fast an object moves and is usually expressed as the distance travelled per time of travel. 

    • The speed of a wave refers to the distance travelled by a given point on the wave (crest) in a given interval of time. 

    • The speed of a wave is thus measured in metres/second i.e. m/s.

9.4 Simple Harmonic Motion

• Definition:

  • Simple Harmonic Motion (SHM) is described by Newton's Second Law through the following equations:

    • x = x_0(cos(ωt))

    • v = -ωx_0(sin(ωt))

    • a = -ω^2(x_0)(cos(ωt))

  • Here, 

    • x_0 is the amplitude (maximum displacement), 

    • x is the displacement, 

    • v is the velocity, a is the acceleration, and 

    • ω is the angular frequency related to the period (T) through ω= 2π/T.

• Energy Changes:

  • In SHM, there's an exchange between kinetic energy (KE) and potential energy (PE) throughout the motion, while the total energy (KE + PE) remains constant.

9.5 Difference between Periodic, Oscillation and Simple Harmonic Motion

• Periodic Motion

  • A motion repeats itself after an equal interval of time. For example, uniform circular motion.

  • There is no equilibrium position.

  • There is no restoring force.

  • There is no stable equilibrium position.

• Oscillation Motion

  • To and fro motion of a particle about a mean position is called an oscillatory motion in which a particle moves on either side of the equilibrium (or) mean position is an oscillatory motion.

  • It is a kind of periodic motion bounded between two extreme points. 

  • For example, the oscillation of a simple pendulum, spring-mass system.

  • The object will keep on moving between two extreme points about a fixed point is called the mean position (or) equilibrium position along any path (the path is not a constraint).

  • A restoring force will be directed towards the equilibrium position (or) mean position.

  • In an oscillatory motion, the net force on the particle is zero at the mean position.

  • The mean position is a stable equilibrium position.

• Simple Harmonic Motion or SHM

  • It is a special case of oscillation, along with a straight line between the two extreme points (the path of SHM is a constraint).

  • The path of the object needs to be a straight line.

  • A restoring force will be directed towards the equilibrium position (or) mean position.

  • The mean position in Simple Harmonic Motion is a stable equilibrium.

Summary:

• At maximum displacement, PE is at its maximum while KE is zero.

• At zero displacement, KE is at its maximum while PE is zero.

• At minimum displacement, PE is at its maximum while KE is zero.

• Total energy remains constant throughout the motion.

9.6 Single-Slit Diffraction

• Nature of Single-Slit Diffraction:

  • Distinct diffraction patterns emerge when light passes through a single slit comparable in size to the wavelength of the light.

• Representation of Diffraction Pattern:

  • This pattern is represented by plotting light intensity against the angle of diffraction.

• Angle of Diffraction for First Minimum θ:

  • sinθ = λ/a

    • Here, λ is the wavelength, and a is the size/length of the slit.

  • sinθ_m = m(λ/D)

    • Where m is the order of the maximum, D is the distance from the slit to the screen.

9.7 Interference

• Young’s Double-Slit Experiment:

  • In this experiment, interference patterns are observed when light passes through two slits, creating regions of constructive and destructive interference.

• Modulation of Double-Slit Pattern by Single-Slit Diffraction:

  • A true double-slit pattern shows closely spaced dark and light areas, superimposed over the single-slit pattern. 

  • The single-slit profile modulates the double-slit pattern.

• Multiple Slit and Diffraction Grating Interference Patterns:

  • Multiple Slit Interference Patterns:

    • θ = m(λ/a)

  • Diffraction Grating Interference Patterns:

    • dsinθ = mλ

      • Where d is the distance between gratings, m is the order of the maximum, and λ is the wavelength.

9.8 Resolution

• Diffracting Aperture Size:

  • The resolution of an image passing through a diffracting aperture improves with a larger aperture diameter.

• Resolution of Two-Source Systems:

  • The Rayleigh criterion determines whether two points are just resolved. The minimum angular separation θ for two points to be just resolved is given by θ = 1.22(λ/a)

• Importance of Resolution in Technology:

  • Resolution is crucial in technologies like CDs, DVDs, electron microscopes, and radio telescopes for optimal performance.

9.9 Doppler Effect

• Doppler Effect Equations for Sound Waves:

  • Four Doppler effect equations cater to different cases based on the movement of the source and/or observer.

• Doppler Equation for Electromagnetic Waves:

  • change in f = (v/c)f

  • This equation is applicable when the velocity of the observer is much smaller than the speed of light.

• Application in Speed Detectors:

  • The Doppler effect is utilized in speed detectors where the frequency shift indicates whether a car is approaching or moving away, enabling the calculation of the car's speed.

Chapter 10: Fields

10.1 Describing Fields

• Gravitational Fields

  • Specific energy and energy density are vital for quantifying the energy released during combustion.

  • A gravitational field is a region where a small test mass experiences a force due to another mass. 

• Electrostatic Fields

  • An electrostatic field is a space where a small positive test charge experiences a force per unit charge.

• Electric Potential and Gravitational Potential

  • Electric Potential

    • Given by electric potential difference (voltage).

    • Or v = w / q_moved

  • Gravitational Potential

    • Gravitational potential due to mass M is the work done per unit mass required to move a test mass from infinity to a point P.

    • Gravitational potential is always negative.

    • The potential at infinity is zero.

    • To find potential due to multiple masses, add potentials due to individual masses.

• Field Lines

  • Field lines show the path a test particle would take in a force field, revealing its direction and strength.

• Equipotential Surfaces

  • Points with the same gravitational potential form equipotential surfaces.

  • Field lines are normal to equipotential surfaces.

  • Density of field lines is proportional to field strength.

  • Near Earth's surface, gravitational field strength is relatively constant with height.

10.2 Fields at Work

• Potential and Potential Energy

  • Electric Potential Energy

    • Given by Coulomb's constant (k), fixed charge (Q), test charge (q), and radius (r).

    • Defined as the capacity for doing work by a change in position of the positive test charge.

  • Gravitational Potential Energy

    • Given by mass M, mass m, and radius (r).

    • Work done required to move an object from infinity to a point P.

    • Gravitational potential energy is always negative.

• Potential Gradient

  • Gravitational potential gradient is ΔV/Δr, related to gravitational field strength (g) by g = -ΔV/Δr = GM/r².

  • It represents the slope of a graph plotting gravitational potential against distance from the mass.

• Potential Difference

  • Defined as the work done by moving a positive test charge between two points in an electric field.

  • Voltage across an electrical component is required for current flow.

  • Cells or batteries provide the necessary potential difference.

• Escape Speed

  • The escape speed of a planet is given by G(M/R)^0.5.

  • Escape speed is the minimum speed needed for an object to reach infinity from a planet's surface.

  • Objects launched at or above escape speed won’t return due to gravity.

• Orbital Motion, Orbital Speed, and Orbital Energy

  • Orbital Motion

    • Gravitation provides the centripetal force for orbital motion.

    • Orbital period is proportional to the average radius by Kepler’s third law.

  • Orbital Speed

    • Given by (GM/r)^0.5, where G is the gravitational constant, M is the mass, and r is the radius.

  • Orbital Energy

    • Kinetic energy, gravitational potential energy, and total energy are defined for an orbiting satellite.

• Forces and Inverse-Square Law Behavior

  • Inverse-Square Law Graphical Representation

    • Graphical representation of inverse-square law behavior for gravitational and electric fields.

  • Gravitational Field

    • Graphical representation of the gravitational field in accordance with the inverse-square law.

  • Electric Field

    • Graphical representation of the electric field in accordance with the inverse-square law.

Chapter 11: Electromagnetic Induction

11.1 Electromagnetic Induction

Motional EMF:

• Concept:

  • When a conductor moves through a magnetic field, it induces an electromotive force (EMF).

• Physics:

  • Free electrons in the conductor experience a force due to the magnetic field, leading to a separation of charges and an electric field within the conductor.

• Formula:

  • The induced EMF (ε) is given by ε=BvL, where

    • B is the magnetic field strength,

    • v is the velocity of the conductor, and

    • L is the length of the conductor perpendicular to the direction of motion.

• Equilibrium:

  • The induced EMF continues until the electric force from the built-up charge balances the magnetic force, eε=evB.

Magnetic Flux and Faraday’s Law

• Magnetic Flux (Φ): Quantified as representing the total magnetic field moving through an area A at angle

• Faraday’s Law: The induced EMF in a circuit is equal to the negative rate of change of magnetic flux through the circuit

Lenz’s Law:

• The direction of the induced EMF and current is such that it opposes the change in magnetic flux that produced it, conserving energy.

• Demonstrated by considering the direction of force on electrons due to the magnetic field and the resulting direction of current flow.

• Applications and Implications

  • Lenz’s and Faraday’s laws are foundational for the functioning of electrical generators, transformers, and induction-based technologies.

  • The laws also provide a deeper understanding of the interplay between electricity and magnetism, showcasing the principle that changing magnetic fields can induce electrical currents.

Transmission of Power

• Alternating Current (AC)

  • AC is produced by an AC generator, where a coil rotating in a magnetic field induces an EMF due to electromagnetic induction.

  • AC changes direction periodically, with the EMF and current represented as sinusoidal functions over time.

• The AC Generator

  • Converts mechanical energy into electrical energy using electromagnetic induction.

  • A coil rotates within a magnetic field, cutting through magnetic field lines, thus inducing an EMF and current.

  • The EMF (ε) Induced in the coil is proportional to the rate of change of magnetic flux, given by

    • ε=N(dΦ/dt)

      • N is the number of turns in the coil.

Root Mean Square (RMS) Quantities

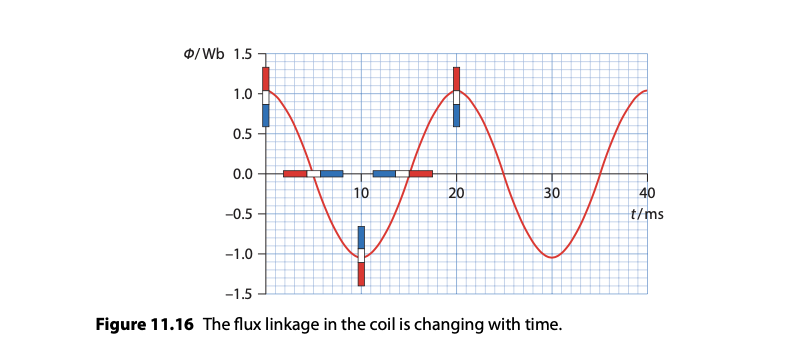
• RMS values provide a measure of the equivalent steady DC values that would produce the same power.​

• peak voltage and current respectively, divided by root 2, gives the respective rms values.

• RMS values are used because power in an AC circuit depends on these average values rather than the peak values.

• The Transformer:

  • A device that changes the voltage level of AC without changing its frequency through electromagnetic induction.

  • Consists of primary and secondary coils around a core, with the voltage change ratio determined by the ratio of turns in the coils

  • Power loss in transformers occurs mainly due to eddy currents, which are minimized by laminating the core, and magnetic hysteresis.

• Transformers and Power Transmission:

  • Step-up transformers increase voltage, reducing current for efficient long-distance power transmission, minimising power loss (P=I²R)

  • Step-down transformers reduce voltage to safe levels for domestic and industrial use.

  • Power plants use high voltages to transmit power over long distances to reduce energy loss.

Diode Bridges and Rectification

• Diode bridges convert AC to direct current (DC).

  • Half-wave rectification uses a single diode to allow current in only one direction, resulting in a loss of half the waveform.

  • Full-wave rectification uses a bridge rectifier to use both halves of the AC waveform, improving efficiency.

  • During one half-cycle, two diodes conduct, allowing current flow in one direction; during the opposite half-cycle, the other two diodes conduct, maintaining the direction of current flow.

11.2 Capacitance

• Definition and Basic Concept:

  • Capacitance (C): The ability of a system to store charge per unit voltage, defined as C, where

    • q is the charge

    • V is the potential difference

    • Unit of capacitance is the farad (F), where 1 F = 1 C/V.

  • Capacitance of a Parallel Plate Capacitor

    • Depends on the geometry: where

      • d is the distance between plates

      • is the permittivity of the medium

      • A is the plate area.

• Effect of Dielectric on Capacitance

  • Inserting a dielectric material between the plates of a capacitor increases its capacitance by reducing the electric field, which allows the capacitor to store more charge for the same voltage.

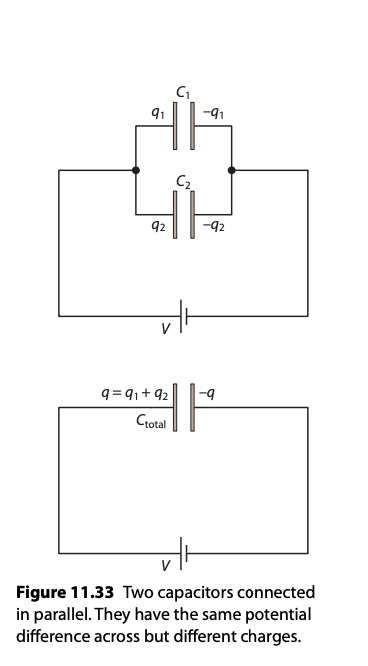
  • Capacitors in Parallel and Series

    • Parallel Configuration:

      • Capacitances add up ( C_total = C₁₊C₂₊C_3…….)

    • Series Configuration:

      • Inverses of capacitances add up.

• Energy Stored in a Capacitor

  • Represents the work done to charge the capacitor.

  • Charging and Discharging a Capacitor

    • Charging: When connected to a voltage source, the capacitor charges up following an exponential curve, approaching its maximum charge asymptotically.

    • Discharging: The stored energy in the capacitor is released when the circuit is closed, discharging exponentially to zero.

  • Capacitors in Rectification

    • Used in conjunction with diodes in power supply circuits to smooth the output from rectifiers.

    • During the half-cycle when the AC is in the correct direction, the capacitor charges up, and during the opposite half-cycle, it discharges, providing a more continuous DC output.

Chapter 12: Quantum and nuclear physics

12.1 Interaction of Matter with Light

Photons and Light

• Light is composed of particles called photons.

• Each photon has an energy given by E=hf, planck's constant(h)*frequency of wave.

• Photons also have momentum, described by p=𝜆h

The Photoelectric Effect

Occurs when light ejects electrons from a material's surface, provided the light's frequency is above a certain threshold.

Observations include:

• Intensity of light does not affect the energy of emitted electrons.

• Emitted electron energy is directly proportional to the light frequency.

• Below a minimum frequency, no electrons are emitted, regardless of light intensity.

• Electron emission occurs without any noticeable delay.

Einstein’s Explanation of the Photoelectric Effect

• Proposed that light consists of photons with quantized energy.

• A photon's energy must exceed the material's work function.

• The maximum kinetic energy () of an emitted electron is given by =hf-

• The stopping voltage in a photoelectric experiment is related to the maximum kinetic energy of the photoelectrons by eV=hf-, where e is the charge of the electron, and V is the stopping potential

Matter Waves

Proposed by de Broglie, suggesting particles such as electrons exhibit wave properties, with a wavelength.

Pair Annihilation and Pair Production

• Pair Annihilation: A particle and its antiparticle annihilate to produce photons.

• Pair Production: A photon creates a particle-antiparticle pair, requiring the presence of a nucleus to conserve momentum and energy.

Quantization of Angular Momentum

Bohr's model suggests that angular momentum of an orbiting electron is quantized,

Where n is the shell level

Leads to discrete or quantized energy levels within the atom, which is calculated using the following formula:

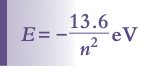
The Wave Function

A mathematical function describing the quantum state of a particle.

The square of its amplitude represents the probability density of finding a particle in space.

The Uncertainty Principle

Stated by Heisenberg, it asserts a fundamental limit to the precision with which pairs of physical properties, like position(x), and momentum (p), given by

The Electron in a Box (Particle in a One-Dimensional Box Model)

Demonstrates quantization of energy levels; an electron confined in a 'box' can only occupy certain energy states. illustrates quantum mechanical properties such as discrete energy levels and the wave nature of particles.

Quantum Tunneling

A phenomenon where particles can pass through a potential barrier, even if they do not possess enough energy to overcome the barrier classically. Has significant implications for nuclear fusion, semiconductor devices, and various other quantum phenomena.

12.2 Nuclear Physics

Rutherford Scattering

Rutherford's gold foil experiment: Alpha particles are scattered by a thin gold foil, leading to the discovery of the dense, positively charged nucleus.

Scattering formula: Scattering angle distributions can be predicted, but the formula for distance of closest approach

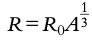
Distance of Closest Approach

Represents the nearest point an alpha particle comes to the nucleus during scattering, determined by the particle's kinetic energy and the electric charge of the nucleus.

Deviations from Rutherford Scattering

At very close distances, alpha particles deviate from the expected path, hinting at nuclear forces and the structure of the nucleus.

Nuclear Energy Levels

• Similar to electrons in atoms, nucleons (protons and neutrons) within the nucleus also have quantized energy levels.

• Transitions between these levels can emit or absorb gamma rays, analogous to the photon emissions or absorptions in atomic transitions.

The Neutrino

• Hypothesized to account for the conservation of energy, momentum, and angular momentum in beta decay.

• A nearly massless and chargeless particle, it interacts with matter only through the weak nuclear force.

Radioactive Decay Law

The rate of decay of a radioactive isotope is described by

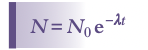
Where A is the activity, that is the number of nuclei decaying per second, lambda is the decay constant which is the probability a nucleus decays in a second. The decay constant multiplied by number of nuclei is the activity.

Minimum Formula

We know from diffraction that if the de Broglie wavelength λ of the electrons or neutrons is about the same as that of the nuclear diameter, the electrons and neutrons will diffract around the nuclei.A minimum will be formed at an angle θ to the original direction according to:

Chapter 13: Relativity

13.1 The beginnings of relativity

Reference frames

• Relative perspective in Physics clarifies different points of view.

• Example: Car velocity varies based on the observer's frame.

• Reference frame: Defines an object's position using coordinates and time events.

  • Your current sitting position is a reference frame.

  • Despite Earth's motion, you feel stationary.

Examples of reference frames

• Everyday examples illustrate perspectives.

• Car moving down a road:

  • People on opposite sides perceive its direction differently.

• Train leaving a station:

  • Person A (platform) sees Person B (train) moving right.

  • Person B (train) sees Person A (platform) moving right.

Inertial frames of reference

• Inertial reference frame:

  • Non-accelerating frame.

  • All inertial frames move at constant velocity relative to each other.

• No absolute reference frame:

  • Nothing is completely stationary in the Universe.

  • Everything is in motion relative to each other.

Newton’s Postulates of Time and Space

• Inertial reference frames are employed due to consistency with Newton's laws.

• Galilean Relativity encompasses this principle.

• Example: An object in an inertial frame moves in a straight line with constant velocity unless acted upon by force.

  • Corresponds to Newton's first law.

• Laws of Physics remain consistent across frames if moving at constant velocity.

• Cartesian coordinate system is commonly used for reference frames.

  • Represents points in space in 3D and 2D.

• Infinite inertial frames in the Universe; methods to transition between them exist.

13.2 Lorentz transformations

Lorentz transformations

• Observers moving relative to each other may differ in numerical values of space and time coordinates for events, and yet they unanimously agree on the numerical value of the speed of light in a vacuum.

• The Lorentz transformation equations establish the connection between values in one reference frame and those in another.

• These equations supersede the Galilean transformation equations, which become inadequate when dealing with speeds approaching that of light.

The Postulates of Special Relativity

• Galilean relativity: Newton's laws are applicable in all inertial frames.

• Newton treated space and time as fixed and absolute.

• The time interval between events in one frame equals that in another.

• Exception at speeds close to light's: Space and time become relative.

• The length of the object or time interval depends on the frame of reference.

• Velocity addition is applicable at much lower speeds than light's (c).

• Doesn't work for speeds approaching c.

• Example: Rocketship traveling at 0.7c releasing probe at 0.5c results in 1.2c, violating the light speed limit.

Einstein’s Two Postulates of Relativity

• First Postulate

  • The laws of physics are the same in all inertial frames.

  • In its own reference frame, an object is always stationary.

  • Conducting a physics experiment produces the same results on a moving train or stationary platform.

• Second Postulate

  • The speed of light (c) in vacuum is constant in all inertial frames.

  • Different observers measure the speed of light as c, irrespective of their motion.

  • The runner holding the flashlight measures the speed of light as c.

  • A stationary observer sees the speed of light as c, not affected by the runner's velocity.

  • Applies only to the speed of light, not to any other speed.

Simultaneity in Special Relativity

• "Simultaneous" denotes occurring at the same time.

• Relativity of simultaneity:

  • Whether events are simultaneous depends on the observer's reference frame.

• In one frame, events at different points in space appear simultaneous.

• In another frame moving relative to the first, events seem sequential.

• Contrast with Galilean relativity where simultaneity was absolute.

Illustrative Example

• Person B in the moving train carriage switches on a lamp.

  • Observe light reaching points X and Y simultaneously.

• Person A stationary on the platform observes the train passing.

  • Sees light move to both ends of the carriage at speed c (Einstein's second postulate).

  • Light reaches point X before point Y due to the carriage's motion.

• The difference in arrival times is exaggerated in the diagram; the actual difference is very small and depends on the train's speed.

Visualization using Space-Time Diagrams

• Diagrams aid in understanding simultaneity in different frames of reference.

Chapter 14: Engineering Physics

14.1 Rigid Bodies and Rotational Dynamics

Torque

• Torque measures the rotational effect of a force acting on an object.

• Calculation: τ=r×F, where r is the moment arm and F is the force.

• When force is applied perpendicular to the object (θ=90∘), sinθ is 1.

• Directional considerations are crucial for torque calculations.

Moment of Inertia

• Moment of inertia (I) resists rotational acceleration.

• Calculation: I=∑miri²

• Shapes have different moments of inertia due to mass distribution.

• Moment of inertia (I) is a property of an object that describes its resistance to rotational motion.

• It depends on how mass is distributed relative to the axis of rotation.

• Objects with larger moments of inertia require more torque to achieve the same angular acceleration.

• It is akin to mass in linear motion, representing the object's inertia in rotation.

• Moment of inertia varies based on the shape and distribution of mass within the object.

• It is a fundamental concept in rotational dynamics, essential for understanding the behavior of rotating bodies.

Rotational and Translational Equilibrium

• Rotational equilibrium occurs when the net torque acting on an object is zero, meaning it remains stationary or rotates at a constant angular velocity.

• Translational equilibrium happens when the net force acting on an object is zero, resulting in no change in its velocity, whether stationary or moving with constant velocity.

• In rotational equilibrium, the sum of all torques acting on the object must balance out to zero.

• In translational equilibrium, the vector sum of all forces acting on the object must cancel out, resulting in no acceleration.

• Objects in rotational equilibrium may still be in translational motion if their center of mass is moving at a constant velocity.

• Both types of equilibrium are crucial concepts in understanding the stability and motion of objects, whether static or dynamic.

Angular Acceleration

• Angular acceleration (α) describes how quickly the rotational speed of an object changes over time.

• It indicates whether the rotation is speeding up or slowing down.

• It is influenced by the net torque acting on the object.

• Objects with larger moments of inertia require more torque to achieve the same angular acceleration.

• Angular acceleration is a fundamental concept in understanding rotational dynamics and engineering applications involving rotating systems.

• Calculation: ω=2πf or ω= 2π/T.

• Angular acceleration: α= Δω/Δt​

Equations of Rotational Motion for Uniform Angular Acceleration

• Equations analogous to linear motion equations.

• Equations of rotational motion for uniform angular acceleration describe the relationship between angular displacement, initial and final angular velocities, angular acceleration, and time.

• These equations are analogous to the equations of motion in linear kinematics.

• They provide a framework for predicting the behavior of rotating objects undergoing constant angular acceleration.

• The equations allow for the calculation of various parameters such as final angular velocity, angular displacement, and time taken for rotation under uniform acceleration.

• They are essential tools in analyzing rotational dynamics problems and designing mechanisms involving rotating components.

• Understanding these equations enables engineers and physicists to predict and control the motion of rotating systems accurately.

Newton’s Second Law Applied to Angular Motion

• Newton's Second Law applied to angular motion states that the net torque acting on an object is proportional to the rate of change of its angular momentum.

• Mathematically, it can be expressed as τ=Iα, where τ is the net torque, I is the moment of inertia, and α is the angular acceleration.

• This law illustrates that a torque applied to an object will cause it to undergo angular acceleration, similar to how a force applied to an object causes linear acceleration.

• It implies that the change in angular momentum of an object is directly proportional to the torque applied and occurs in the direction of the torque.

• Newton's Second Law for angular motion provides a fundamental principle for analyzing rotational dynamics problems and designing systems involving rotating components.

• It is crucial for understanding the behavior of rotating objects under the influence of external torques and for predicting their motion accurately.

Conservation of Angular Momentum

• Total angular momentum is conserved when no external torques act.

• Conservation of angular momentum states that the total angular momentum of a system remains constant when no external torques act upon it.

• Mathematically, it can be expressed as L_initial = L_final, where L represents angular momentum.

• This principle applies to isolated systems where external torques are absent, allowing angular momentum to be conserved.

• When external torques are present, angular momentum can still be conserved if the net external torque acting on the system is zero.

• Conservation of angular momentum plays a crucial role in various physical phenomena, such as the motion of celestial bodies, spinning objects, and collisions involving rotational motion.

• Understanding this principle helps in predicting the behavior of rotating systems and designing mechanisms to utilize or conserve angular momentum efficiently.

Rotational Kinetic Energy

• Rotational kinetic energy refers to the energy associated with the rotational motion of an object.

• It is analogous to linear kinetic energy but involves rotational motion instead of linear motion.

• Rotational kinetic energy depends on both the moment of inertia of the object and its angular velocity.

• Objects with larger moments of inertia or higher angular velocities possess greater rotational kinetic energy.

• Rotational kinetic energy is an important concept in understanding the behavior of rotating systems and is often used in engineering applications, such as designing rotating machinery and analyzing the stability of rotating objects.

• Rotational kinetic energy calculation: KErot = (½)Iω²  where I is the moment of inertia and ω is the angular velocity.

14.2 – Thermodynamics

The First Law of Thermodynamics

• The First Law of Thermodynamics, also known as the law of conservation of energy, states that energy cannot be created or destroyed in an isolated system; it can only change forms.

• This law is based on the principle of energy conservation and applies to all forms of energy, including thermal, mechanical, chemical, and nuclear energy.

• Q=ΔU+W where Q is heat, ΔU is internal energy change, and W is work.

• The equation implies that the change in internal energy of a system is equal to the heat added to the system minus the work done by the system.

• The First Law of Thermodynamics has various practical applications, such as understanding heat engines, refrigerators, and chemical reactions, and it forms the basis for the study of thermodynamics and energy conservation principles.

The Second Law of Thermodynamics

• The Second Law of Thermodynamics states that the total entropy of an isolated system tends to increase over time.

• Entropy is a measure of the disorder or randomness of a system.

• The Second Law implies that natural processes tend to move towards states of higher entropy, leading to an increase in overall disorder within the system.

• One consequence of the Second Law is the concept of irreversibility; many natural processes are irreversible and result in an overall increase in entropy.

• The Second Law also predicts the direction of heat flow, stating that heat energy spontaneously flows from hotter regions to colder regions, but not vice versa, without external intervention.

• The law imposes limitations on the efficiency of heat engines and refrigeration systems, indicating that perfect conversion of heat into work is impossible.

• Understanding the Second Law of Thermodynamics is crucial in various fields, including physics, chemistry, engineering, and environmental science, as it governs the behavior of energy and entropy in natural systems.

• Entropy increases or remains the same in any cyclic process.

• Heat cannot flow from colder to hotter without work.

Entropy

• Entropy is a thermodynamic quantity that represents the amount of disorder or randomness in a system.

• It is a measure of the number of possible microscopic arrangements or states that a system can have.

• Entropy tends to increase in natural processes, leading to a spontaneous move towards greater disorder.

• Systems with higher entropy are associated with greater randomness or unpredictability in the distribution of their constituent particles or energy.

• Entropy is closely related to the concept of probability; systems are more likely to be found in states with higher entropy.

• The Second Law of Thermodynamics states that the total entropy of an isolated system tends to increase over time.

• Entropy plays a crucial role in various fields, including thermodynamics, statistical mechanics, information theory, and ecology.

• Understanding entropy helps in analyzing the behavior of systems undergoing transformations and in designing efficient processes in engineering and science.

• Calculation: ΔS = Qrev / T

Cyclic Processes and pV Diagrams

• Heat engines operate in cycles converting heat to work.

• pV diagrams represent cyclic processes.

• Cyclic processes occur when a system returns to its initial state after a series of thermodynamic changes.

• These processes are common in heat engines, refrigerators, and other cyclic systems.

• pV diagrams, also known as pressure-volume diagrams, graphically represent the changes in pressure and volume of a system during a thermodynamic process.

• In cyclic processes, pV diagrams form closed loops, indicating that the system returns to its initial state after completing a cycle.

• The area enclosed by the loop on a pV diagram represents the net work done by or on the system during the cycle.

• Heat engines, such as car engines, operate in a cyclic manner by taking in heat, converting some of it into work, and expelling the rest.

• pV diagrams provide valuable insights into the efficiency and performance of heat engine cycles, such as comparing them to idealized cycles like the Carnot cycle.

• Understanding cyclic processes and pV diagrams is essential for analyzing and optimizing the operation of various thermodynamic systems, including engines, refrigerators, and heat pumps.

Isovolumetric, Isobaric, Isothermal, and Adiabatic Processes

• Isovolumetric process: Volume remains constant, resulting in changes in internal energy only.

• Isobaric process: Pressure stays constant, allowing for both work done and changes in internal energy.

• Isothermal process: Temperature remains constant, with energy transfer occurring as work done and changes in internal energy.

• Adiabatic process: No heat exchange with surroundings, leading to changes in temperature and pressure through work done alone.

• These processes are essential in thermodynamics and find applications in various systems such as engines, refrigerators, and heat exchangers.

Carnot Cycle

• Most efficient heat engine cycle.

• Comprises two isothermal and two adiabatic processes.

• The Carnot cycle is a theoretical model representing the most efficient heat engine cycle.

• It consists of four reversible processes: two isothermal and two adiabatic processes.

• The cycle operates between two temperature reservoirs, a high-temperature source and a low-temperature sink.

• Heat is absorbed from the source during isothermal expansion and rejected to the sink during isothermal compression.

• The Carnot cycle's efficiency depends solely on the temperatures of the two reservoirs and is the maximum achievable efficiency for a heat engine.

• While an idealized concept, the Carnot cycle provides a standard for assessing the performance of real-world heat engines and refrigeration systems.

Thermal Efficiency

• Efficiency: η= W/Qin

• Maximum efficiency in Carnot cycle:

• ηmax=1−(Tcold/Thot)

• Thermal efficiency is a measure of how effectively a device converts heat into useful work or energy.

• It is calculated as the ratio of the useful work output to the heat input.

• The efficiency of heat engines, refrigerators, and other thermal systems is often expressed in terms of thermal efficiency.

• For example, in heat engines, thermal efficiency is given by the ratio of the work done by the engine to the heat input from the high-temperature reservoir.

• The Carnot cycle sets the maximum theoretical efficiency for heat engines operating between two temperature reservoirs.

• Improving thermal efficiency is a key goal in engineering to optimize the performance and energy consumption of thermal systems.

Chapter 15: Imaging

15.1 Introduction to Imaging

Converging and Diverging Lenses

• Converging lenses, thicker in the middle, converge light rays to form real images when rays cross, unless the object is at the focal point or nearer.

• Diverging lenses, thinner in the middle, diverge light rays, forming virtual images where rays appear to have come from.

Lens Properties and Image Formation

• Principal axis: an imaginary line passing through the lens center perpendicular to its surfaces.

• Focal point: where parallel rays converge or appear to diverge after passing through the lens.

• Focal length: the distance from the lens center to the focal point, determining the lens's strength.

• Optical power: measured in diopters (D), defined as the inverse of focal length (P = 1/f).

• Ray diagrams predict image formation assuming a thin lens and rays near the principal axis.

• Real images form where rays converge; virtual images form where rays appear to diverge.

Magnification and Special Cases

• Magnification calculated as the ratio of image height to object height (m = hi/ho = -v/u).

• Special cases include objects beyond the focal point forming real, inverted images, and objects at or closer than the focal point forming magnified, upright, virtual images.

• Magnifying glasses use converging lenses for magnification, producing virtual, upright images.

• The near point is the closest clear focus point for the normal eye, typically 25 cm, while the far point is the farthest clear focus point, typically at infinity.

Lens Aberrations and Mirrors

• Spherical aberration causes distorted images due to the lens's inability to focus all rays at the same point, which can be reduced by adapting the lens shape or using only the central lens portion.

• Chromatic aberration results from the lens's inability to bring rays of different colors to the same focus, which can be reduced by combining lenses with different shapes and refractive indices.

• Mirrors follow similar principles to lenses, with curved mirrors susceptible to spherical aberration.

• Telescope resolution depends on lens quality, aperture size, and wavelength, with improvements achieved through large apertures and small wavelengths.

Radio Telescopes

• Radio telescopes experience less atmospheric interference, and arrays using interferometry techniques can enhance resolution further.

15.2 Imaging Instrumentation

Microscope

Objective Lens and Eyepiece

• The objective lens forms a real magnified image of an object just beyond its focal point.

• The eyepiece acts as a magnifying glass to produce an inverted, magnified, and virtual final image.

Resolution and Magnification

• Resolution, the ability to distinguish separate points, is often more critical than magnification.

• Two objects are considered just resolvable if the angle they subtend is larger than 1.22λ/b (Rayleigh’s criterion), where b is the diameter of the receiving aperture.

Telescope

Objective Lens or Mirror

• The objective lens of a telescope forms a diminished, real, and inverted image of a distant object at its focal point.

• Reflecting telescopes use converging mirrors as their objectives.

Mounting Configurations

• Various mounting configurations exist, such as Newtonian and Cassegrain, each offering specific advantages.

Atmospheric Limitations and Solutions

• Optical telescopes on Earth's surface face limitations due to atmospheric effects.

• Placing telescopes on orbiting satellites overcomes these limitations.

Radio Telescopes and Interferometry

• Radio telescopes receive radio waves, which are less affected by the atmosphere.

• Interferometry techniques allow higher resolution by combining signals from multiple telescopes.

15 Fibre Optics

Data Transmission

• Data transmission occurs through electrical or infrared pulses in cables, with digital data represented by a large number of pulses, each having two possible levels.

• Transmission effects include attenuation, causing signal intensity loss with distance, and dispersion, resulting in pulse broadening and intensity decrease.

Fiber Optic Advantages and Principles

• Fiber optics offer advantages over copper, including lower attenuation, higher data rates, and immunity to electromagnetic interference.

• Total internal reflection ensures efficient wave propagation within fibers.

• Dispersion causes, such as waveguide and material dispersion, can be mitigated by using graded-index fibers or monochromatic light.

Additional Information

Attenuation Equation

• The intensity of a signal confined to an optic fiber decreases exponentially with distance along the cable (I = I0 * e^(-μx)).

15.4 Medical Imaging

X-ray Imaging

Absorption and Attenuation

• X-rays are absorbed and scattered differently by various body tissues, forming images based on these variations.

• The intensity of a parallel beam of X-rays decreases exponentially with distance due to absorption and scattering: I=I₀e^−μx , where μ is the linear attenuation coefficient.

• Absorption due to the photoelectric effect is a primary means of X-ray attenuation, dependent on the proton number (Z) of the atoms present.

Tissue Density and Attenuation

• Different tissue densities affect the intensity of the detected X-ray beam.

• The attenuation of X-rays can be characterized by the half-value thickness, representing the thickness of a medium that reduces transmitted intensity to half its previous value.

Image Quality Considerations

• X-ray quality is vital for high-quality images, balancing intensity, contrast, and safety.

Ultrasound Imaging

Wave Propagation and Reflection

• Ultrasound waves are directed into the body and reflect off boundaries between different tissues.

• Acoustic impedance determines the percentage of incident waves that reflect at tissue boundaries.

Pulse Transmission and Resolution

• Ultrasound waves are transmitted in pulses, with resolution improved by having several complete ultrasound waves in each pulse.

• Different ultrasound scan types, such as A-scans and B-scans, provide information about tissue position and size.

Frequency and Attenuation

• Higher ultrasound frequencies offer better resolution but also undergo more attenuation.

Magnetic Resonance Imaging (MRI)

Proton Spin Resonance

• MRI utilizes proton spin resonance in strong magnetic fields to produce images.

• Protons precess around the direction of the external magnetic field, with the rate of precession proportional to the field's strength.

Resonance and Imaging

• Resonance occurs when protons are subjected to an oscillating electromagnetic field of the same frequency.

• MRI provides three-dimensional images through gradient magnetic fields in three perpendicular directions.

Health Risks and Safety

Imaging Risks

• X-ray processes carry a health risk due to ionizing radiation exposure.

• MRI, not involving ionizing radiation, is considered safer than X-ray processes.

Additional Information

Attenuation Equation

• The intensity of a parallel beam of X-rays decreases exponentially with distance (I = I₀ e^{{-\mu x}}), where μ is the linear attenuation coefficient.

MRI Principles

• MRI utilizes proton spin resonance in strong magnetic fields to produce images.

• Resonance occurs when protons precess around the direction of the external magnetic field at the Larmor frequency, proportional to the field's strength.

Chapter 16: Astrophysics

16.1 Stellar Quantities

Objects in the Universe

• The solar system includes the Sun, eight planets, dwarf planets, moons, asteroids, and comets.

• The universe is vast; our solar system is a mere speck.

Types of Celestial Bodies

• Single star: Luminous plasma sphere held by gravity.

• Binary star: Two stars orbiting a common center.

• Black hole: Singularity in space-time.

• Cepheid variable: Star with varying luminosity, aiding distance measurement.

• Clusters of galaxies: Gravitationally affected groups of galaxies.

• Constellation: Pattern of unbound stars visible from Earth.

• Dark matter: Cold, non-radiating matter inferred from physics.

• Galaxies: Stars, gas, and dust bound by gravity.

• Main sequence star: A normal star undergoing hydrogen fusion in order to turn into helium.

• Neutron stars: Dense stars with uncharged neutrons.

• Nebula: Cloud of dust, gasses, helium, and hydrogen.

• Planets: Celestial bodies orbiting a star.

• Supernova: Highly energetic stellar explosions marking the end of a star's life cycle.

  • Type Ia Supernova: Results from the explosion of a white dwarf in a binary star system.

  • Type Ib/c Supernova: Associated with the collapse of massive, hydrogen-poor stars.

  • Type II Supernova: Arises from the collapse of massive stars with a significant hydrogen envelope.

• White dwarfs: The remnants of low to medium-mass stars after they have exhausted their nuclear fuel.

The Nature of Stars

Stability and Equilibrium

• Star stability depends on the equilibrium between gravity and radiation pressure.

• Nuclear fusion maintains equilibrium, preventing collapse.

Units in Astrophysics

• Lightyear (ly): Distance light travels in one year in the vacuum of space. Approximately 9.461 × 10¹² kilometers.

• Parsec (pc): Parallax arcsecond, a unit based on stellar parallax. Approximately 3.09 × 10¹³ kilometers.

• Astronomical Unit (AU): Average distance from Earth to the Sun. Approximately 1.496 × 10⁸ kilometers.

• Megaparsec (Mpc): One million parsecs, often used in cosmological distance measurements. Approximately 3.09 × 10¹⁹ kilometers.

• Solar Radius (R☉): The radius of the Sun, used to express the size of stars. Approximately 6.96 × 10⁵ kilometers.

• Solar Mass (M☉): The mass of the Sun, frequently used for stellar mass comparisons. Approximately 1.989 × 10³⁰ kilograms.

• Light-Minute (lmin): Distance light travels in one minute. Approximately 1.8 × 10¹⁰ kilometers.

Astronomical Distances

• The universe is mostly empty; a light year measures ultra-solar system distances.

• Example: Proxima Centauri - 4.31 light years or 1.3 parsecs away.

• Average distance between stars in a galaxy: 1 pc (3.26 light-years).

• Average distance between galaxies in a cluster: 100 kpc to several Mpc.

Stellar Parallax and Limitations

• Stellar parallax measures space distances using Earth's orbit.

• The parallax of one arcsecond equals one parsec (3.26 light-years).

• There is limited accuracy for distant stars due to small parallax.

Luminosity and Apparent Brightness

• Luminosity: Total power radiated by a star in all directions (measured in watts).

• Apparent brightness: Power received per unit area (measured in W/m²).

• Luminosity decreases with distance following the inverse square law.

  • Inverse square law: I = k / r². States that a physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity. 

    • I = the intensity or strength of a physical quantity,

    • k = a constant

    • r = the distance from the source of the physical quantity.

16.2 Stellar Characteristics and Stellar Evolution

Stellar Spectra

• The absorption spectra can identify elements in stars.

• There are seven spectral classes (O, B, A, F, G, K, M) based on temperature. 

Hertzsprung–Russell (HR) Diagram

• It is a graph relating absolute magnitude, luminosity, classification, and temperature.

• Main sequence stars burn hydrogen; used to estimate star distances.

Mass–Luminosity Relation for Main Sequence Stars

• Luminosity increases with mass for main sequence stars.

Cepheid Variables

• Stars with varying luminosity correlated to period.

• Used as “standard candles” for distance estimation.

Stellar Evolution on HR Diagrams

• Stars form from nebulae, and then undergo nucleosynthesis.

Main-sequence lifetime: Hydrogen fusion into helium.

• Red giants, white dwarfs, neutron stars, and black holes follow fuel depletion.

Chandrasekhar and Oppenheimer–Volkoff Limits

• Chandrasekhar limit: Maximum mass for a white dwarf (about 1.4 solar masses).

  Oppenheimer–Volkoff limit: Maximum mass for a neutron star (2-3 solar masses).

Wien’s Displacement Law

• Describes the relationship between the temperature of a blackbody and the wavelength at which it emits the maximum intensity of radiation.

• Mathematically expressed as λ_max ⋅T = constant where λ_max is the peak wavelength, and T is the temperature in Kelvin.

• Implies that as the temperature of a blackbody increases, the peak emission shifts to shorter (cooler) or longer (hotter) wavelengths.

• Crucial in understanding the color of stars; hotter stars appear bluer, while cooler stars appear redder.

16.3 Cosmology

Big Bang Model

• It is the origin of space and time from singularity expansion.

• It redshifted galaxy observation and Cosmic Microwave Background radiation support.

Cosmic Microwave Background (CMB) Radiation

• It is thermal radiation from the early universe, supporting the Big Bang theory.

Hubble’s Law

• v = Hd describes velocity-distance relationship.

• It is used to estimate the age of the universe.

• The Hubble Constant: denoted as H₀; quantifies the present rate of expansion of the universe, approximately 70 km/s/Mpc.

Accelerating Universe and Redshift (z)

• Supernovae observations show universe expansion acceleration.

• Redshift (z) is determined by the ratio of the observed (λ_observed) to (λ_emitted) emitted wavelengths, expressed as 1+z = (λ_observed / λ_emitted), or in cosmological contexts, z = (Δλ / λ_emitted) = (c⋅Δt)/(λ_emitted), where c is the speed of light and t is time.

• Redshift factor (1+z) affects apparent brightness.

Cosmic Scale Factor (R)

• The cosmic scale factor (R) is a fundamental concept in cosmology, serving as a mathematical representation of the relative expansion or contraction of the universe as a function of cosmic time.

• R is a dynamic parameter that evolves over time, capturing the changing size of the universe. As the universe expands, R increases, reflecting the overall growth of cosmic structures.

• R(t) represents the relative expansion of the universe.

• Einstein’s Theory of General Relativity: Astrophysicists employ Einstein's theory of general relativity to understand the behavior of R in the context of gravitational interactions on cosmic scales.

• Connection to Redshift: The concept of R is intimately connected to the observed redshift (z) in astrophysics. The relationship is expressed by 1+z= 1/R, offering a crucial link between observational data, such as the redshift of distant galaxies, and the underlying dynamics of the expanding universe.