Truth tables

Gates and their truth tables

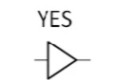
Yes

Input	Output
0	0
1	1

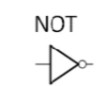
Not

Input	Output
0	1
1	0

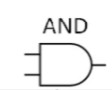
AND

A	B	Output
0	0	0
1	0	0
0	1	0
1	1	1

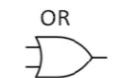
OR

A	B	Output
0	0	0
1	0	1
0	1	1
1	1	1

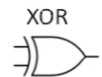
XOR

A	B	Output
0	0	0
1	0	1
0	1	1
1	1	0

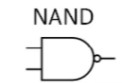
NAND

A	B	Output
0	0	1
0	1	1
1	0	1
1	1	0

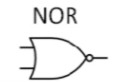
NOR

A	B	Output
0	0	1
0	1	0
1	0	0
1	1	0

XNOR

A	B	Output
0	0	1
1	0	0
0	1	0
1	1	1

SR truth table

S	R	Output
0	0	no change
1	0	setting Q to 1
0	1	resetting Q to 0
1	1	not allowed

Decoder

Tells the entire process exactly what to do

Full-adder

Two XOR gates, two AND gates, one OR gate

Half-adder

One XOR gate and one AND gate

half-adder Truth Table

A	B	Sum	Carry
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Half-Adder Equations

S = A’B + AB’ (XOR gate)

C = AB (AND gate)

Full-adder Truth Table

A	B	Cin	Sum	Cout
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Full adder equations

S = A’B’C + A’BC’ + A’BC + ABC (Two XOR gates)

Cout = (One XOR gate and two AND gate and one OR gate)

XNOR definition

Output is 1 when A and B are the same. Output is 0 when A and B are different

XOR definition

Output is 1 when only one A or B is strictly 1.

NOR definition

Output is 1 when A and B are both 0.

NAND definition

Output is 1 when A or B is 0