biostatistics final review

parametric testing

tests that include statistics in formula

why do researchers prefer parametric testing for hypothesis testing?

tests are more likely to discern significant differences between populations

what are the conditions of parametric testing?

1. fairly spread random sampling

2. samples from different populations must be independent of each other

3. homogeneity of variance: variances of different groups of data must be similar/equal, NOT significantly different

4. must have a normal frequency distribution

non-parametric testing

tests that don't include statistics in formula; occurs when conditions are NOT met

analysis of variance (ANOVA)

determines presence of a significant difference between 4 populations

ANOVA steps to calculate

1. state research and null hypothesis

2. find the variance and mean for each group

3. set up ANOVA table and calculate

4. compare f-statistic value with critical value on F table

5. accept or reject null

degree of freedom equation between groups

k - 1

degree of freedom equation within groups

N - k

total degree of freedom equation

N - 1

sum of squares equation between groups

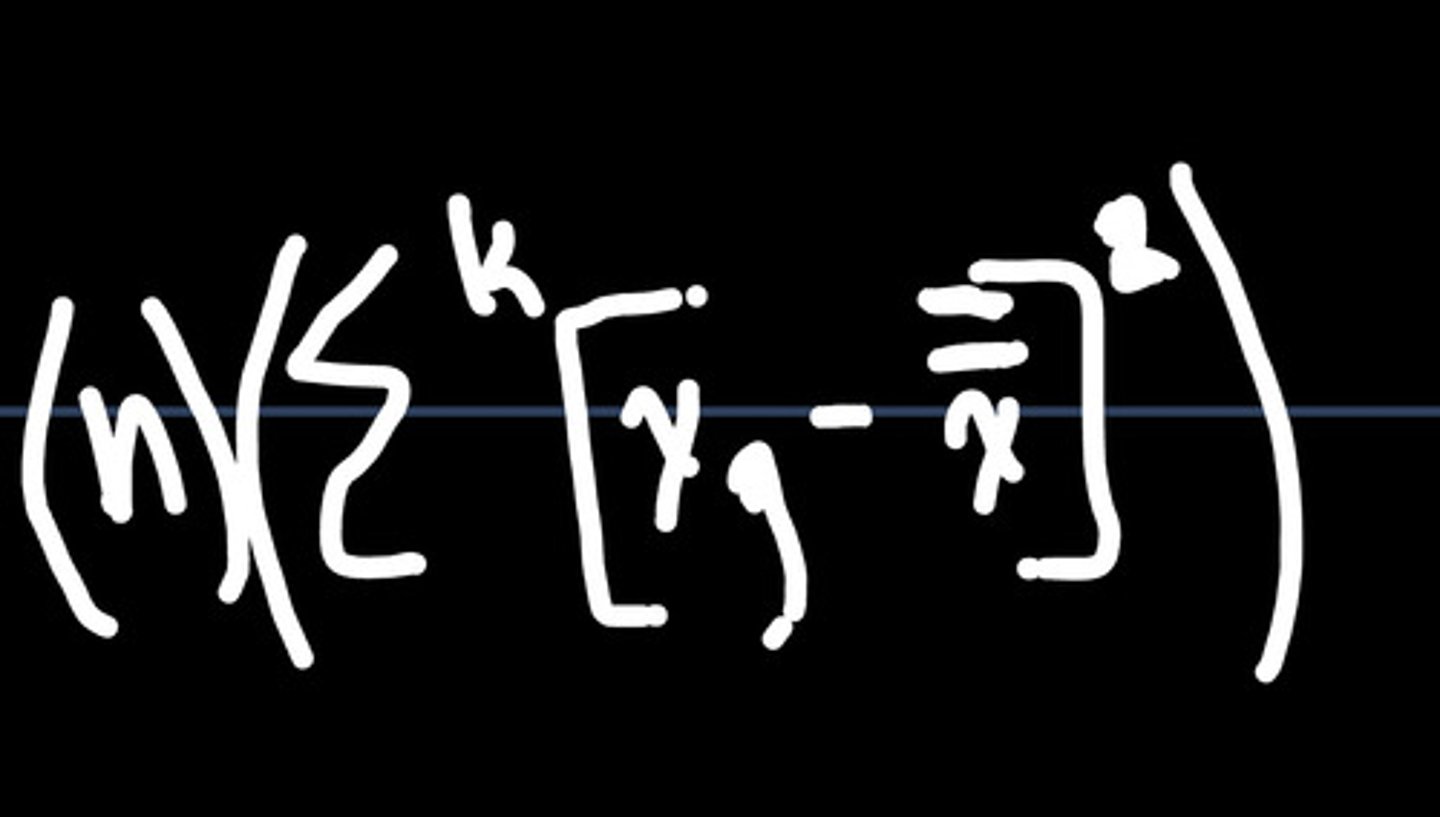
sum of squares equation within groups

variance equation between groups

variance equation within groups

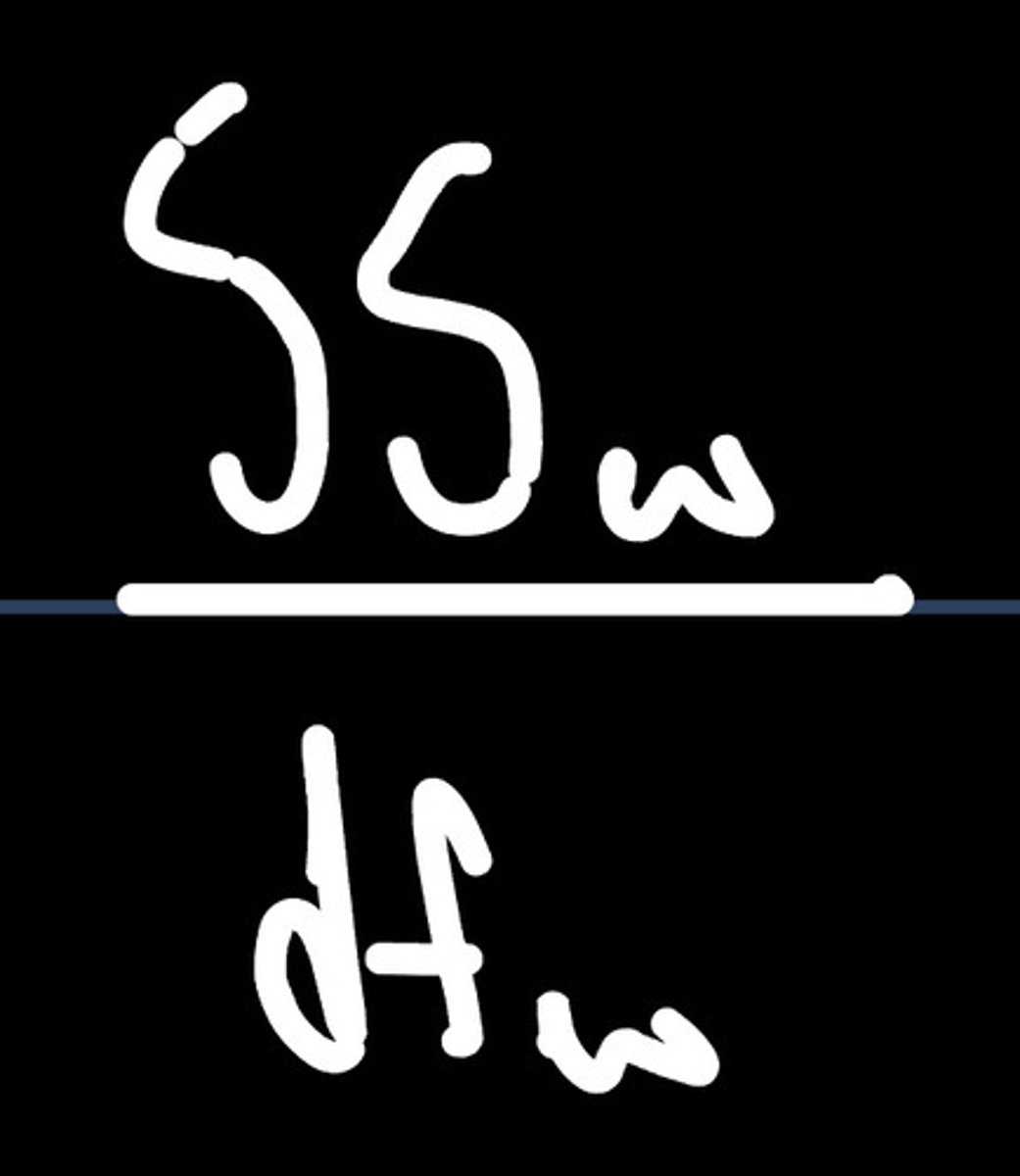
f statistic equation

N

total # of data points

k

# of groups

how to find sum of squares between groups

1. add mean of each group and divide sum by # of groups for grand mean

2. do (group mean - grand mean)^2

3. add all points and multiply by N

how to find sum of squares within groups

positive correlation

both variables increase

negative correlation

both variables decrease

no correlation

1 variable increases and the other stays the same

correlation ___ ___ mean causation

DOES NOT

correlation coefficient

degree of association between -1 and +1

correlation coefficient for positive correlation

r between 0 and 1

correlation coefficient for negative correlation

r between 0 and -1

correlation coefficient for no correlation

r does not equal 0

regression establishes

a causal link between 2 variables

in regression, the independent variable is

fixed on Y axis

in regression, the dependent variable is

fixed on X axis

Tukey's test

used to test the hypothesis that all possible mean pairs are equal

Tukey test steps to calculate

1. subtract all possible mean pairs from each other

2. use HSD equation to calculate critical value on q table

3. compare mean differences with critical value

4. accept or reject null

Tukey's test: HSD equation

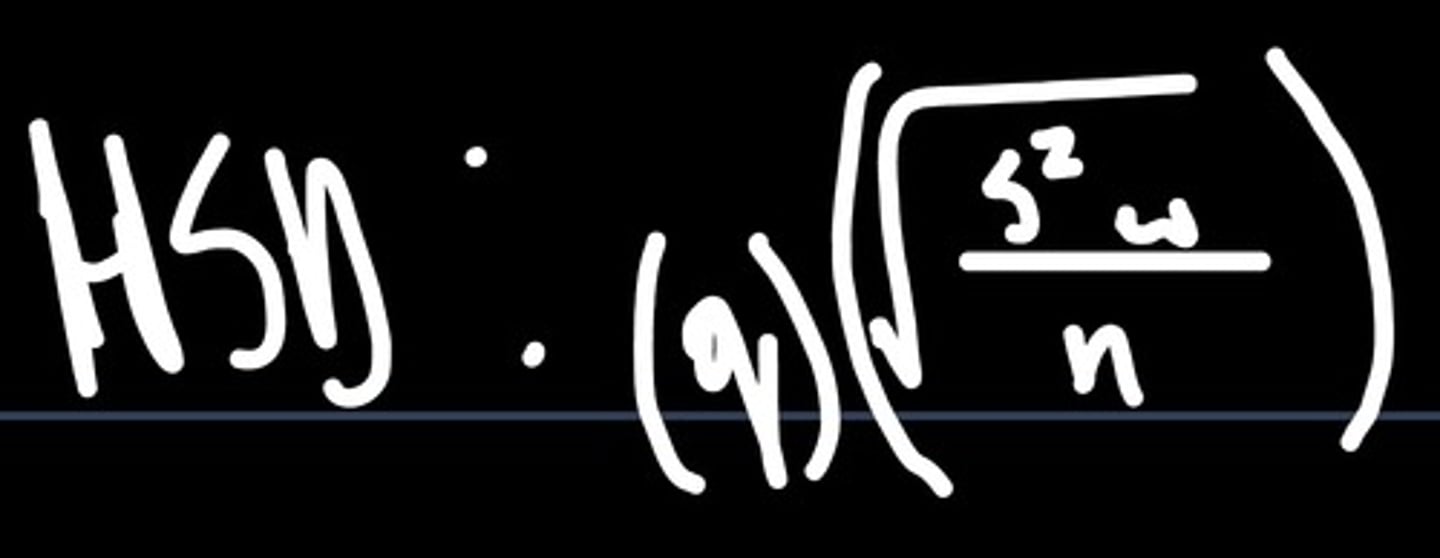
Tukey's test: critical value is found by

combining df within group and k

Tukey's test: if the mean difference is greater than the critical value,

a significant difference exists

U-Test

nonparametric test used to test the hypothesis that there is no significant difference between 2 samples from 2 populations

U-Test steps to calculate

1. arrange all data points in ascending order

2. determine K1 and K2 count by:

k1: from the list, count the # of measurements in sample B smaller than sample A

k2: from the list, count the # of measurements in sample A smaller than sample B

3. the larger value between K1 and K2 is the U-value

4. determine critical value from U-table

5. accept or reject null

U-test: critical value from u-table is found by

n (larger sample size) and n' (smaller sample size)

U-test: to determine K1 and K2 count, what are the values for each #?

tied # is 0.5 points, a # less than is 1 point

Chi-Square test

used to compare frequency distributions

chi-square formula

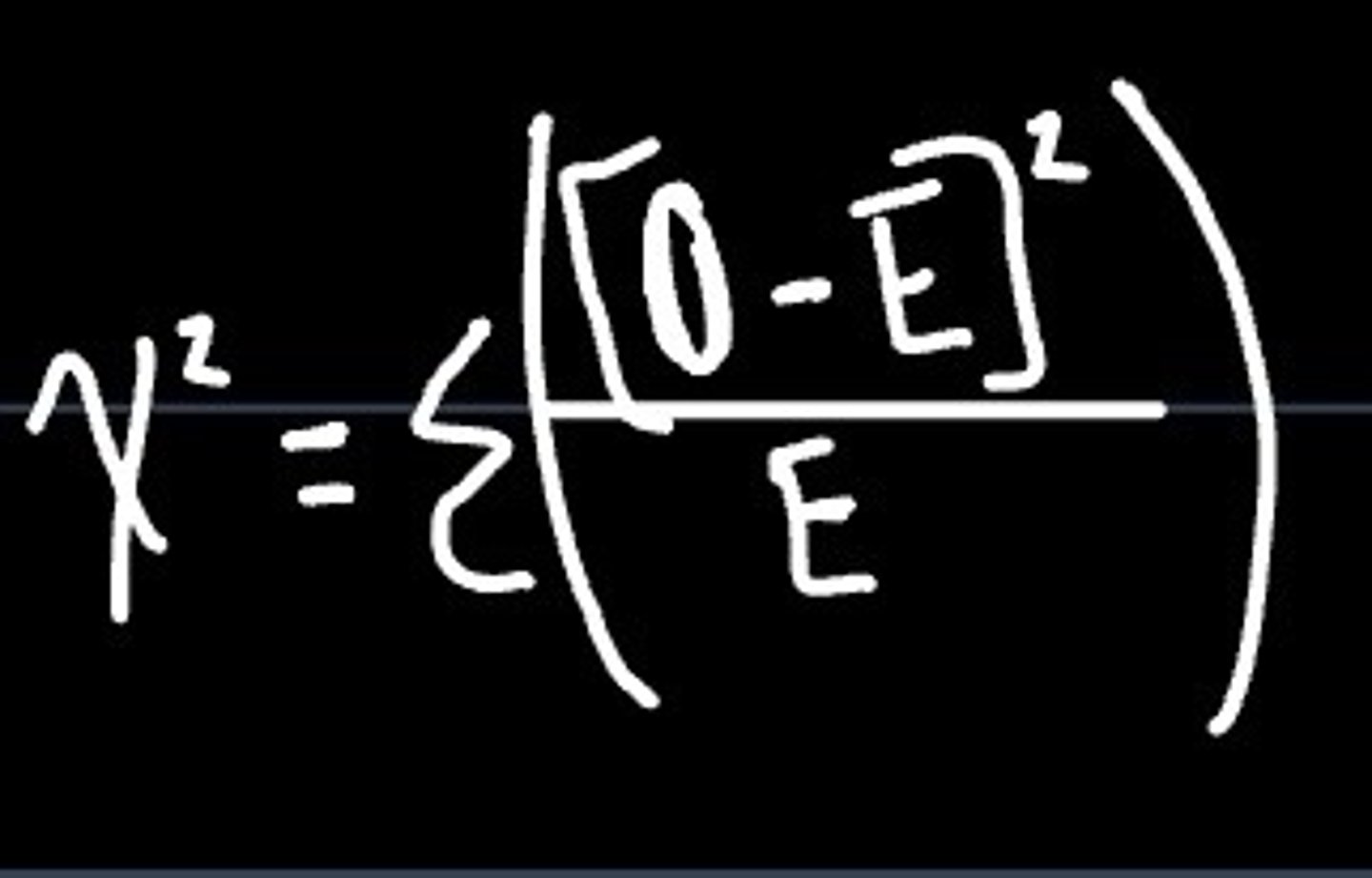
conditions for chi-square

1. random sampling occurs

2. no matching between groups

3. each variable studied must be categorical

4. expected value of the # of sample observations in each level is at least 5

Chi-square steps to calculate with 1 variable

1. write out expected and observed frequencies

2. place data in table and plug in formula for each category

3. compare X^2 value with critical value using chi-square chart

4. accept or reject null

Chi-square: critical value for 1 variable is found by

df (# of categories - 1)

Chi-square steps to calculate with 1 variable

1. identify null and research hypothesis

2. fill in expected frequencies on contingency table

3. calculate expected frequency

4. calculate X^2 and critical value

5. accept or reject null

Chi-square: expected frequency equation

Chi-square: critical value for 2 variables is found by

(# of rows - 1) and (# of columns -1)