Psych 207 - Module 10: Thinking, Problem Solving, and Reasoning

Thinking – Overview

• Going beyond the information given to make sense of situations, solve problems, or generate new ideas.

• Complex, high-level mental process that:

  • Fills gaps in evidence

  • Searches through problem space (mental exploration of possible solutions)

• When used:

  • Whenever we are uncertain about what to do, believe, or desire.

Key Point:

• “Thinking” is a broad term → includes multiple mental activities, not just one process.

Focused Thinking

• Definition: Thinking with a clear starting point and specific goal.

• Characteristics:

  • Mind is on-task.

  • Deliberate and problem-oriented.

• Examples:

  • Solving a math problem.

  • Planning what to cook for dinner using available ingredients.

Unfocused Thinking

Definition: Thinking that is not goal-directed or task-focused.

• Characteristics:

  • Occurs spontaneously or without a specific plan.

  • Can sometimes lead to creative insights.

• Examples:

  • Daydreaming.

  • Mind wandering in class.

  • Incubation stage of creative problem-solving.

How Psychologists Measure Thinking (Cognitive Activities)

1. Responses

   • Observe what answer or choice a person produces.

   • Example: Solving a logic problem or choosing a door in a memory test.

2. Accuracy

   • Correct vs. incorrect answers → reveals understanding or reasoning quality.

   • Example: 80% correct in a mental rotation task suggests effective spatial reasoning.

3. Reaction Time (RT)

   • How long it takes to respond.

   • Example: Longer RT → task is more mentally demanding or involves complex processing.

4. Brain Activity

   • fMRI, EEG, ERP → measures neural activity during thinking tasks.

   • Helps identify which brain regions are involved in specific cognitive functions.

Introspection Method

Definition:

• Detailed, concurrent, and non-judgmental observation of your own conscious thoughts while solving a problem.

Usage:

• Common in reasoning, problem-solving, and decision-making research.

• Participants may verbalize their thought process (“think-aloud” protocols).

Problem:

• Validity issue: How can we externally verify that self-reports truly reflect mental processes?

• People may forget, simplify, or misreport their thought processes.

Types of Problems - Well-Defined Problems

• Definition: Problems with a clear starting point, clear goal, and clear steps to solve it.

• Characteristics:

  1. Clear goal → You know exactly what the solution should be.

  2. Clear beginning and end → You know where to start and when it’s finished.

  3. Clear rules or guidelines → There is a method or formula to follow.

• Examples:

  • Solving a math equation (2x + 3 = 9).

  • Completing a jigsaw puzzle.

1. Easier to present and study → We know they can be solved quickly.

2. Easier to score → Answers are right or wrong, no subjectivity.

3. Easier to modify → Can change difficulty by adjusting steps or rules.

Types of Problems - Ill-Defined Problems

• Definition: Problems with unclear goals, unclear steps, or little starting info.

• Characteristics:

  1. No clear goal → Hard to know when it’s solved.

  2. Few or no clear rules → No obvious formula to use.

  3. Solution can be subjective.

• Examples:

  • Writing an essay on happiness.

  • Deciding on a career change.

Problem Solving Techniques - Generate and Test

Solve a problem by coming up with multiple possible solutions and testing each one to see if it works.

Example:

• Guessing a 3-digit password:

  1. Generate a code (123) → Test → Wrong

  2. Generate another (456) → Test → Wrong

  3. Continue until correct.

Problems with This Technique:

1. Inefficient if there are too many possibilities.

2. Requires working memory to keep track of all tried options → can exceed cognitive capacity.

3. Works best for small, simple problem spaces.

Problem Solving Techniques - Means Ends Analysis

Break a problem into steps (means) to reduce the distance to the goal (end).

• Requires:

  1. Initial state → where you are now

  2. Goal state → what you want to achieve

  3. Intermediate states → steps along the way

  4. Operators → rules or actions you can take to move forward

Example:

• Goal: Get good grades

  • Initial state: Your current grades

  • Intermediate steps: Study schedule, tutoring, completing assignments

  • Operators: Attending class, revising, practice problems

• Key idea: At each step, reduce the difference between current state and goal state.

Tower of Hanoi Problem

Move all disks from the first peg to the third peg, following the rules.

Rules (Constraints):

1. Move only one disk at a time.

2. Never place a bigger disk on top of a smaller disk.

How It Is Solved

1. Subgoals

• Break the problem down into steps (subgoals):

  • Move the smallest disks first to free larger disks.

  • Follow the rule of never stacking big on small.

2. Working Backwards

• Start with the goal in mind:

  1. Visualize the final state (all disks on third peg).

  2. Identify what move must happen right before that.

  3. Continue generating subgoals backward until you reach the initial state.

3. Means-Ends Analysis

• At each step, compare:

  • Current state vs. Goal state

  • Choose moves that reduce the difference while respecting the rules.

The Story of the General and The Tumor Problem

The Tumor Problem (Duncker, 1945)
Given a human being with an inoperable stomach tumor, and rays that destroy organic tissue at sufficient intensity, by what procedure can one free him of the tumor by these rays and at the same time avoid destroying the healthy tissue that surrounds it?

30% got the connection without the hint

75% only got it with the hint (only 75% got it even with the hint)

Analogy

Analogies are a very powerful tool

If you look to the history of science, you’ll find that a number of discoveries that have been made have been linked to the effective use of analogies. For example, William Harvey likening the circulatory system to a water pump. Or, more close to our own hearts here in cognitive psychology, thinking about attention as a spotlight. Perhaps the most famous analogy of them all is that of the relationship between the structure of the hydrogen atom and the solar system. In this analogy, the sun and the planets of the solar system domain are analogous to the nucleus and electron in the atom domain. This example highlights another important role for analogy: that in education and teaching. Many of us may have learned the structure of the atom by comparing it to our solar system. By doing so, it makes it easier to understand and more concrete, by taking something we already know something about, and comparing it to something that we do not.

Blocks to problem solving - examples

• try to draw 4 straight line through 9 dots passing through all

  • Need to think (and draw) outside the box but most people don’t think they’re allowed

• try to turn six matches into 4 triangles

  • Need to make a 3D shape but people wouldn’t think to do so (constrict themself to 2D)

These illustrate how people often go into a problem with faulty assumptions which hinder successful problem solving

Classic Blocks to problem solving

• Mental Set: Tendency to see things in a certain way instead of in another, equally plausible way

• Functional Fixedness: adoption of a rigid mental set towards an object (assuming a screwdriver can only be used as a screwdriver

• Lack of problem specific knowledge or expertise:assumption that most of

  problems are equally unfamiliar to everyone and that people go about solving

  them in basically the same way

  • Other kinds of problems -- skill games, physics, geometry… different than

  puzzles discussed to this point

  • Experts and novices have been found to approach most such problems

    differently

Chase and Simon (1973) --> expert chess players were able to extract more info from brief exposure to a chess board than novices - - Experts could recall more items from a brief exposure than novices This different was only evident when the placements were in a possible game configuration

○ This ties in with their experience with pass plays or moves (they have a larger memory and familiarity with the game)

• Novices do not have this experience and are forced to simply try to maintain this in their working memory

How is reasoning different than thinking?

• Term is often used interchangeably with the term thinking -- overlap between the types of processes used

• When reasoning, we typically have one or more particular goal in mind, whereas thinking is very focused

• Reasoning involves inferences or conclusions drawn from other information

  Two main froms of reasoning:

• Deductive Reasoning: information goes from general to specific (new info is NOT generated)

• Inductive Reasoning: specific info becomes generalized (new info IS generated)

The Wason Selection Tool

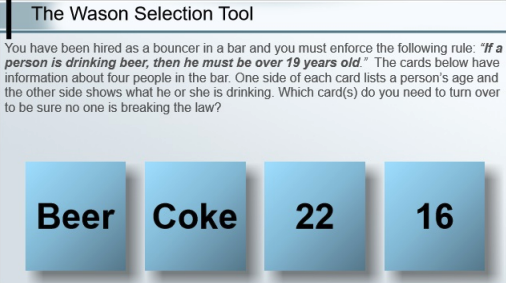
• The second task is much easier for most people --> very few solve the first one correctly (A & 7)

  Conditional reasoning:

  - Griggs and Cox (1982) --> Memory Cueing Explanation

  Argued that certain contents call to mind personal experiences that are relevant to the rule

  -University students do well on this task due to their own personal experience with drinking age laws

  -If there is no relevant experience reasoning about vowels and numbers, performance on the task could not be facilitated

Categorical Syllogisms

people are presented with premises that deal with classes of entities

• Quantifiers provide info about how many members of a class are under consideration (all, none, or some)

• Syllogisms that contain sums or negatives are much more difficult and people are much slower to respond and make more errors

• Content effects can significantly impact logical processing

• Believability effect: people are much more likely to accept a conclusion as valid irrespective of if it logically follows from the premise

Inductive Reasoning

• The Wason 2-4-6 Task is a rule discovery experiment designed by Peter Wason to show how people often seek confirmation rather than disconfirmation when testing hypotheses.

  Setup

  The experimenter gives you a sequence: 2 – 4 – 6.

  Your job: figure out the rule the experimenter used to generate it.

  You can propose other sequences and the experimenter will tell you if they fit the rule.

  You can keep guessing until you think you know the rule.

  What most people do

  People tend to guess something like:

  “The rule is numbers increasing by two.”

  Then they test sequences like 8 – 10 – 12 or 3 – 5 – 7, which fit their hypothesis.

  This is confirmation bias — they test cases that support their theory, not ones that might disprove it.

  The actual rule

  Any three numbers in ascending order.

  (E.g., 1 – 2 – 3, 10 – 20 – 30, 50 – 51 – 100 — as long as they’re increasing.)

Two Theoretical Approaches to reasoning:

1. Mental Logic Approach

• Reasoning = applying formal, language-like rules in the mind.

• Works like mental “if–then” logic steps.

• Good for formal problems, but less realistic for everyday reasoning.

2. Mental Models Approach

• Reasoning = imagining scenarios that match the premises.

• Test conclusions by manipulating these mental models.

• Realistic and meaning-based, but can be biased if all possibilities aren’t considered.

Research - approaches to reasoning

• Evidence for both rule based and mental models based approaches depending on the problem

• Reliance on more rule-based mechanisms when reasoning with content laden material (drinking age problem)

• More visual spatial mental model based mechanisms when reasoning with abstract material in which one can't rely on past experience and knowledge