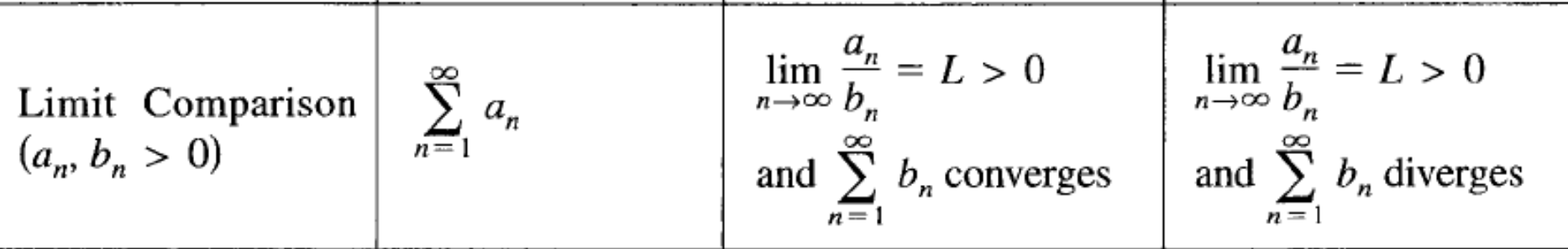AP Calculus AB & BC Formula List

Flashcards for AP Calculus AB & BC Formula List review.

IF THE IMAGE IS TOO SMALL CLICK ON IT TO EXPAND IT!

IF THE IMAGE IS TOO SMALL CLICK ON IT TO EXPAND IT!

Definition of e

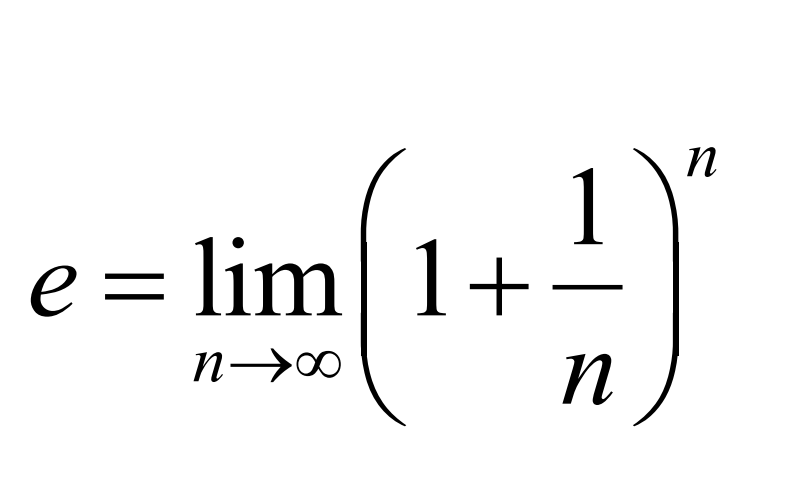
Definition of absolute value

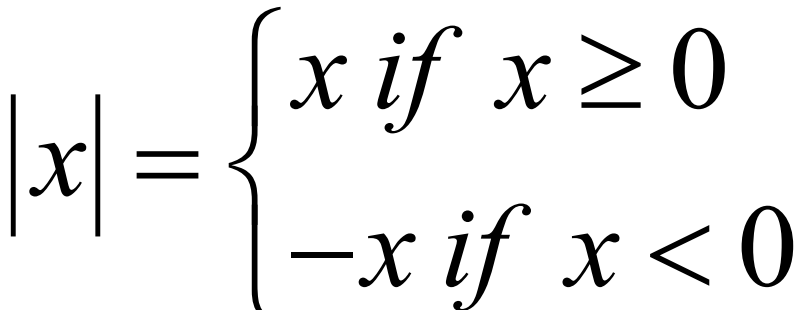
Definition of the derivative.

(Show alt form also!)

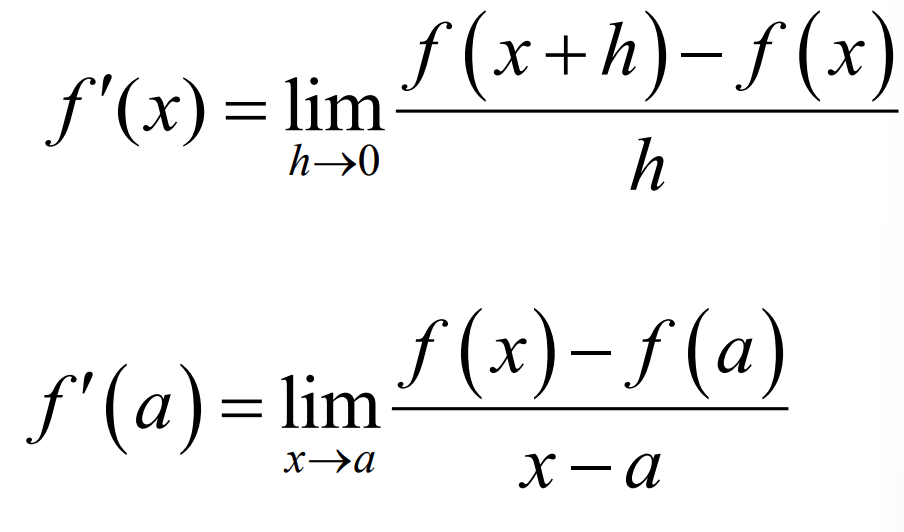
Definition of continuity

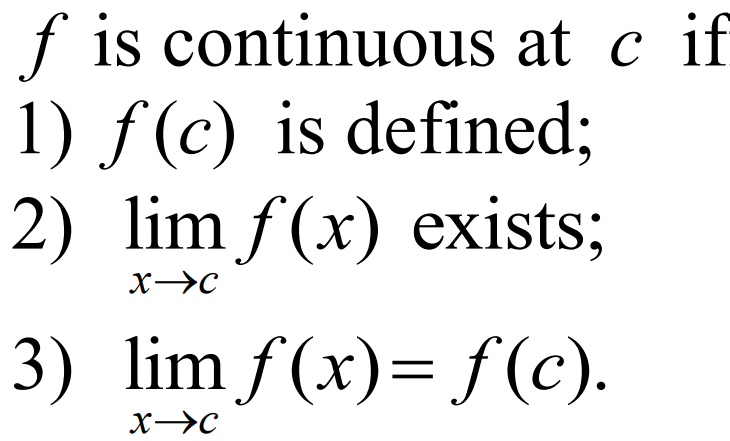
Average change of f(x) on [a, b]

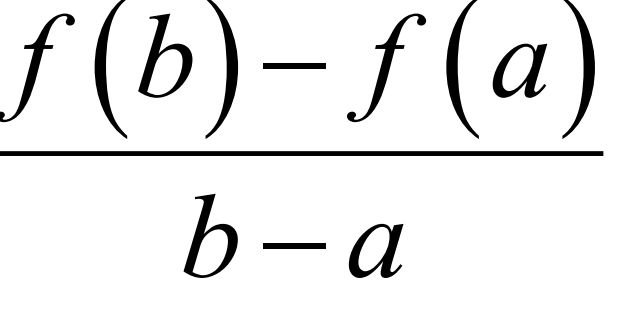
Rolle's Theorem

If f is continuous on [a, b] and differentiable on (a, b) and if f(a) = f(b), then there is at least one number c on (a, b) such that f'(c) = 0.

Mean Value Theorem

If f is continuous on [a, b] and differentiable on (a, b), then there exists a number c on (a, b) such that f'(c) = [f(b) - f(a)] / (b - a).

Intermediate Value Theorem

If f is continuous on [a, b] and k is any number between f(a) and f(b), then there is at least one number c between a and b such that f(c) = k.

Definition of a definite integral

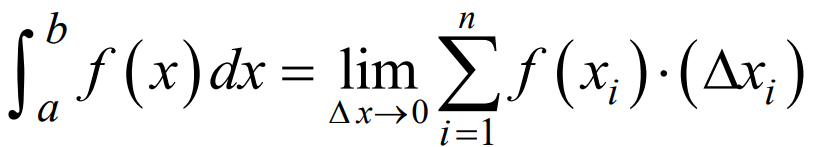
Derivative of a constant

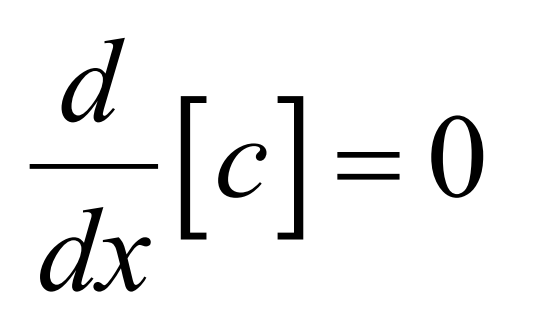
Power Rule

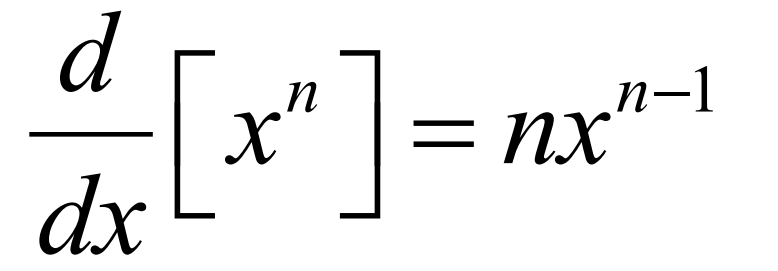
Product Rule

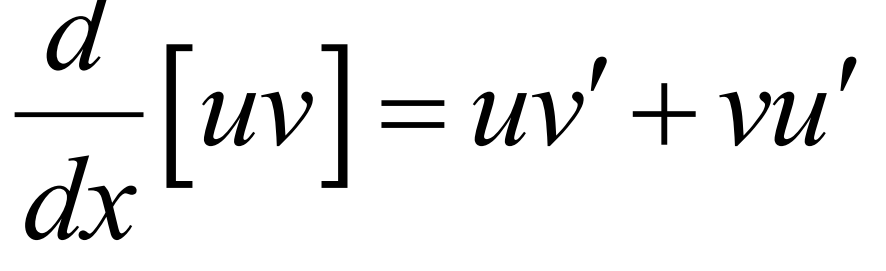
Quotient Rule

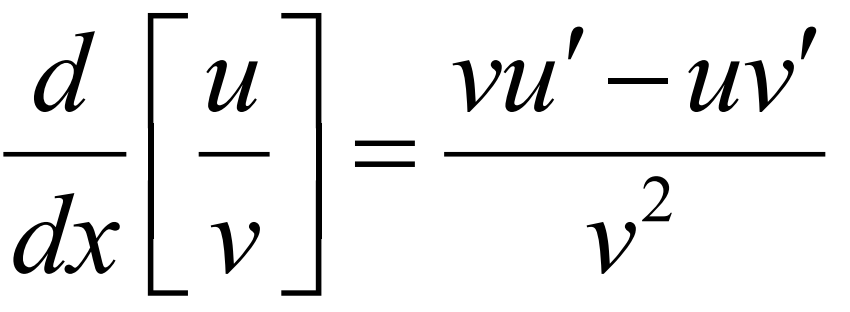
Chain Rule

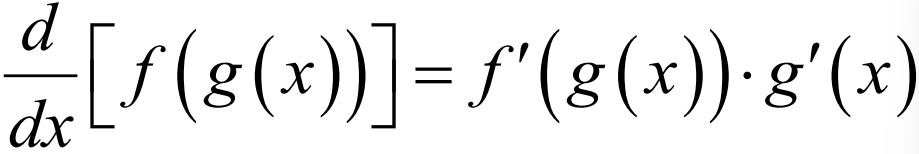
Derivative of sin(u)

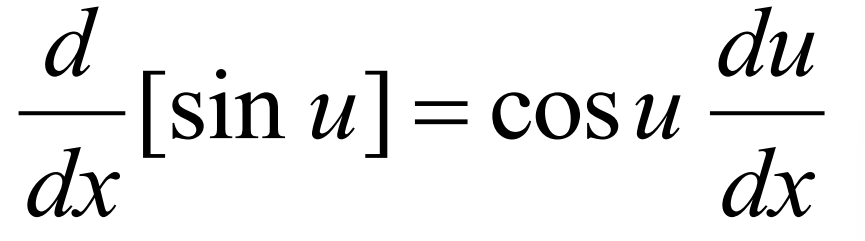
Derivative of cos(u)

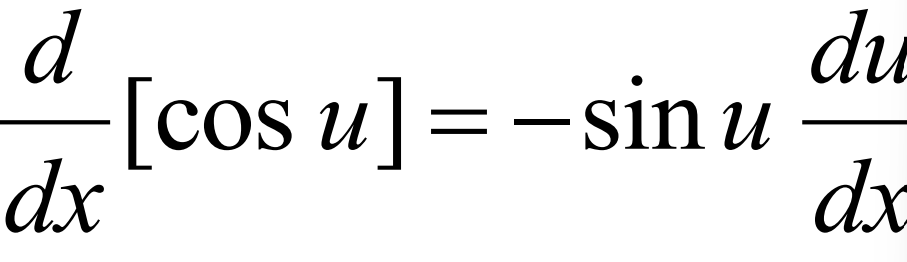
Derivative of tan(u)

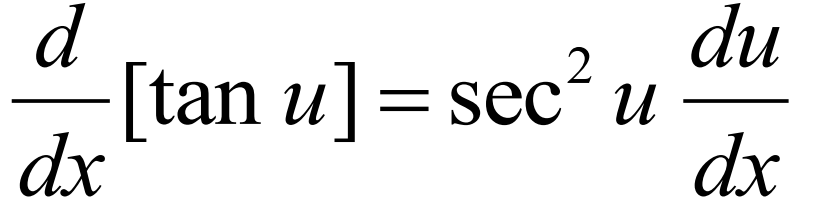
Derivative of sec(u)

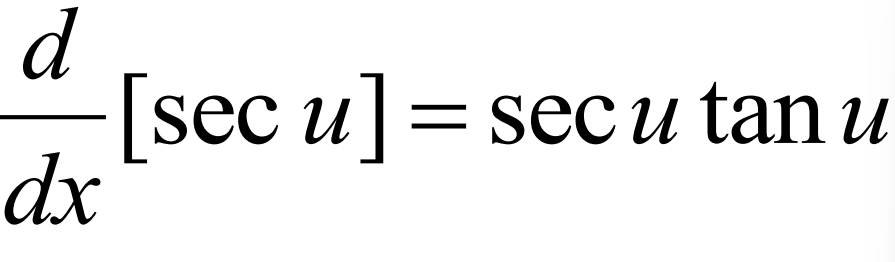
Derivative of csc(u)

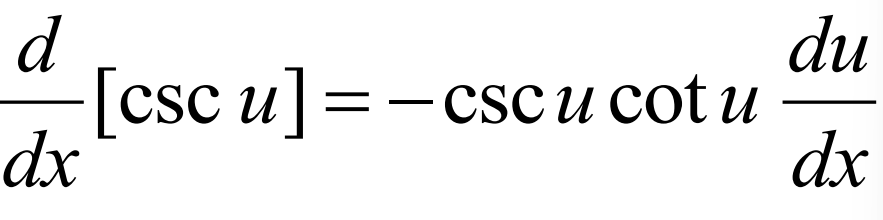
Derivative of cot(u)

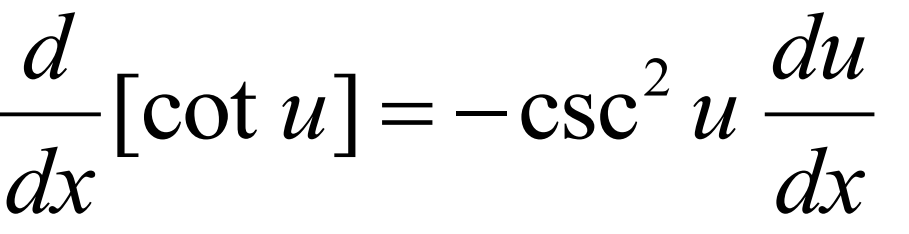
Derivative of ln(u)

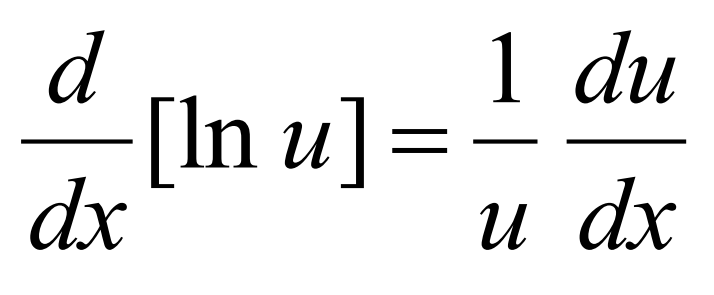
Derivative of log_a(u)

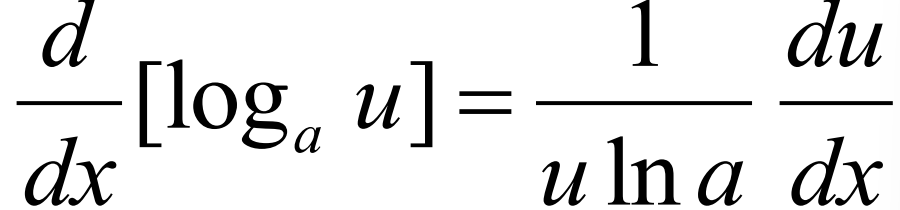
Derivative of e^u

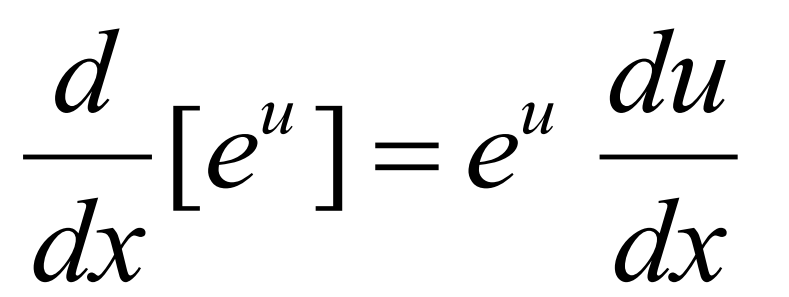
Derivative of a^u

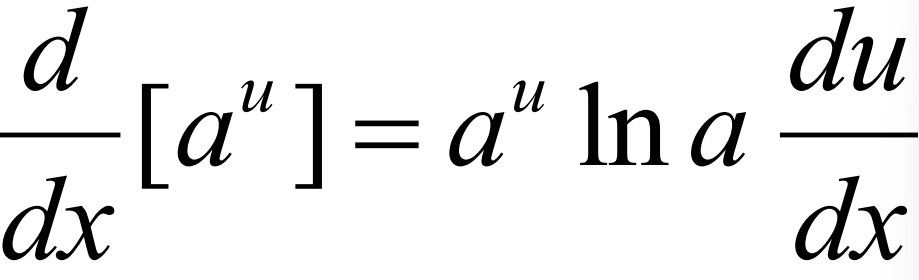
Derivative of arcsin(u)

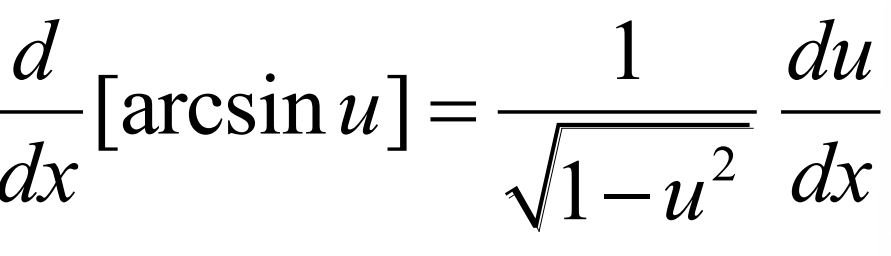
Derivative of arccos(u)

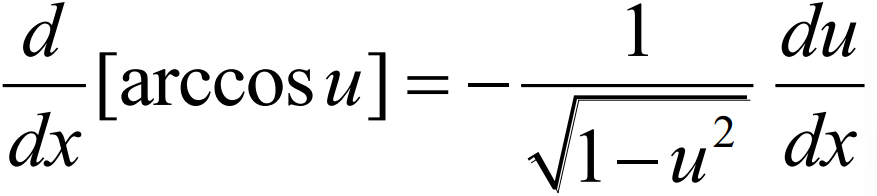
Derivative of arctan(u)

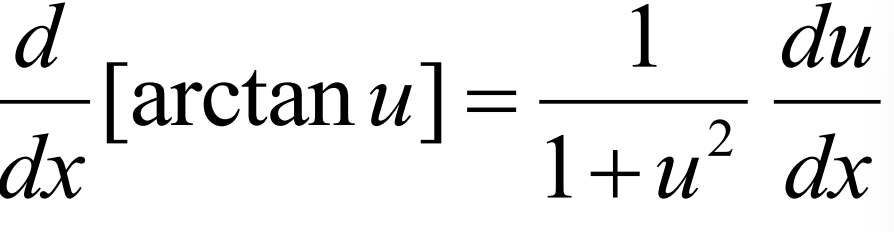
Derivative of arccot(u)

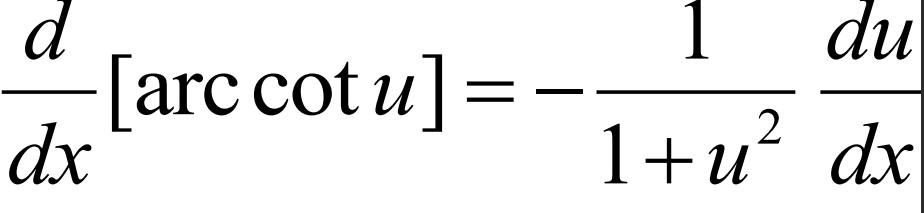
Derivative of arcsec(u)

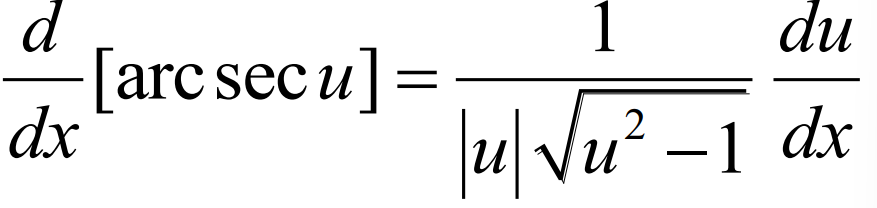
Derivative of arccsc(u)

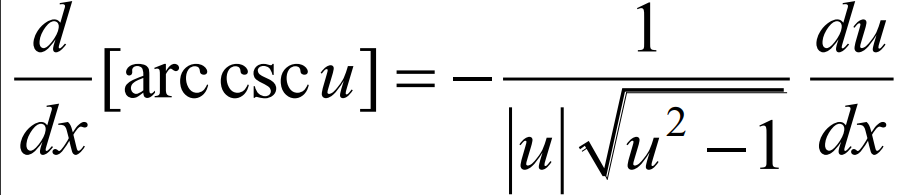
Inverse Function Derivative

Integral of sin(u)du

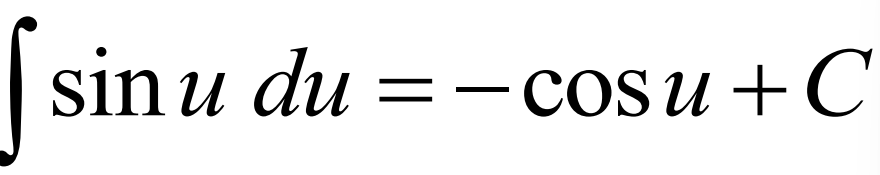
Integral of cos(u)du

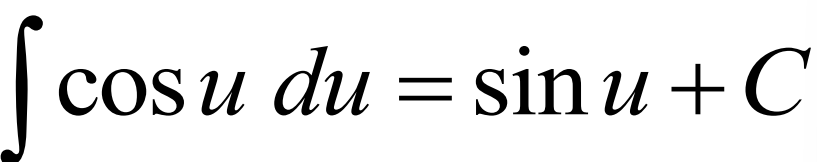
Integral of sec²(u)du

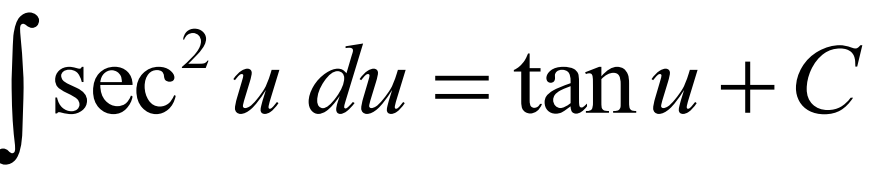
Integral of csc²(u)du

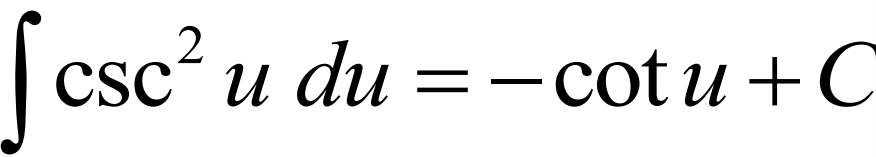
Integral of sec(u)tan(u)du

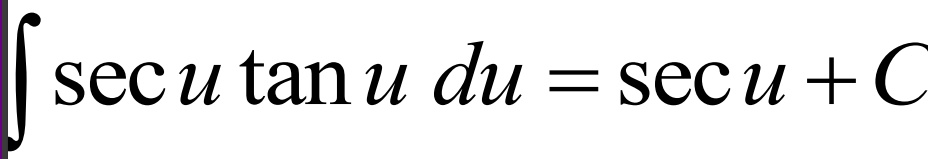
Integral of csc(u)cot(u)du

-csc(u) + C

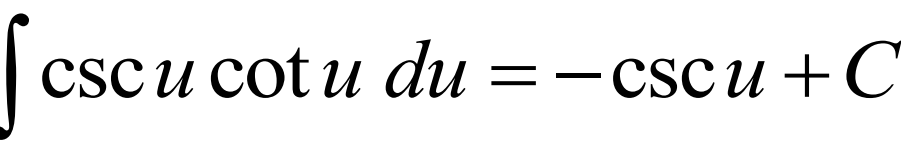
Integral of 1/u

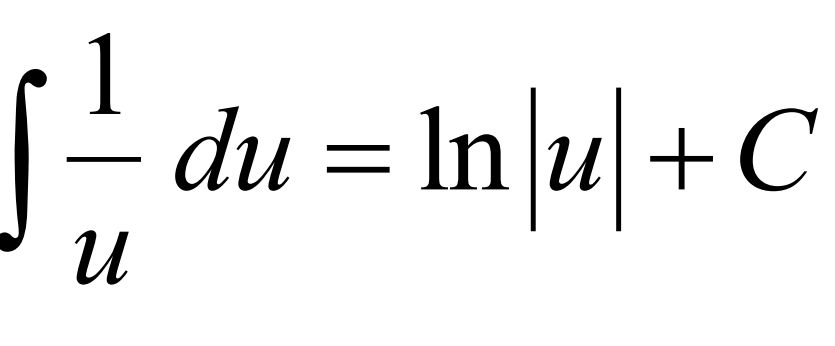
Integral of tan(u) du

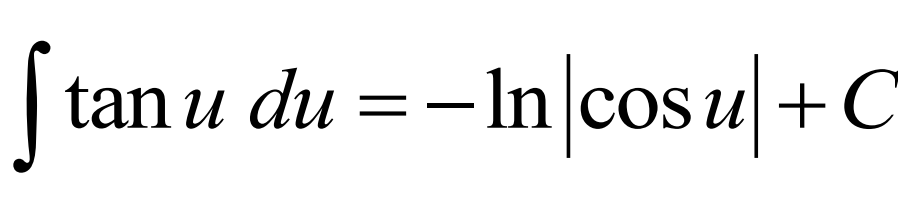
Integral of cot(u) du

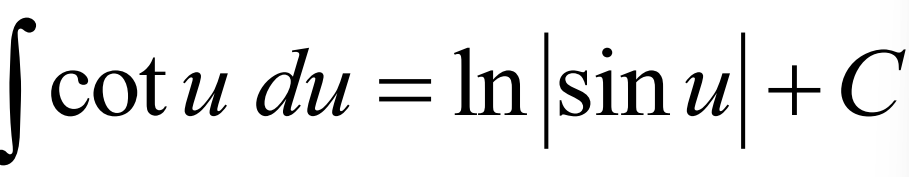
Integral of sec(u) du

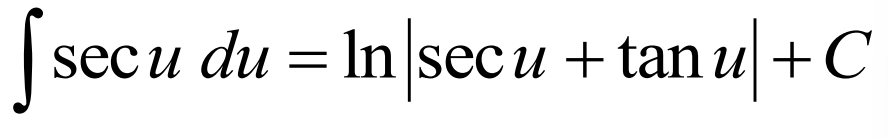
Integral of csc(u) du

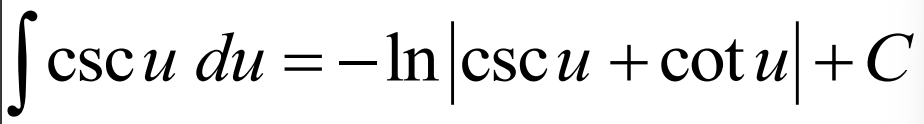
Integral of e^u du

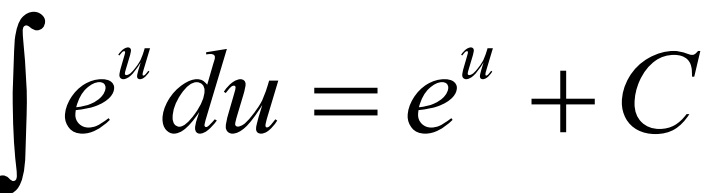
Integral of a^u du

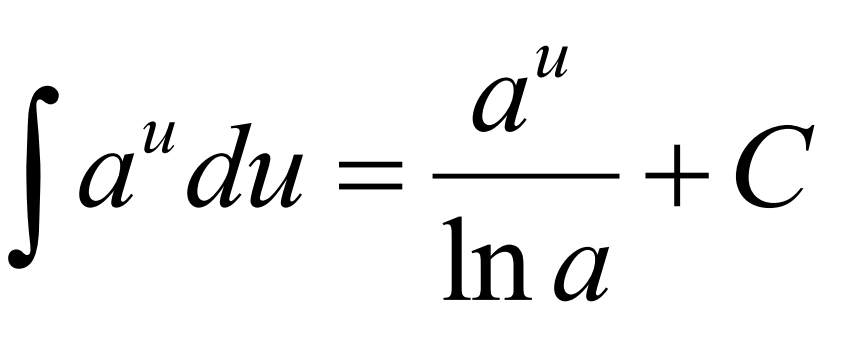
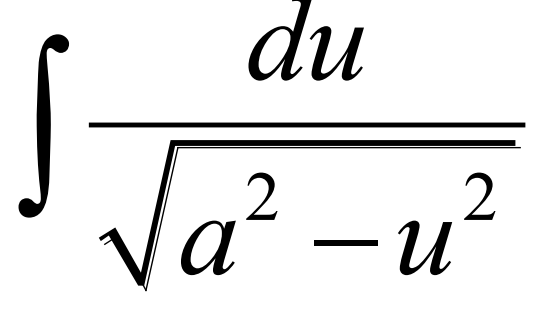
Integral of (see photo)

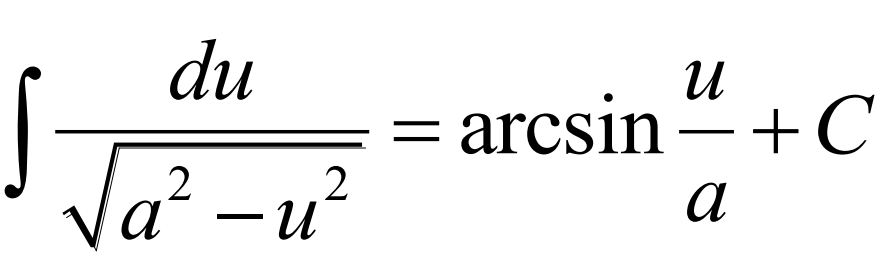
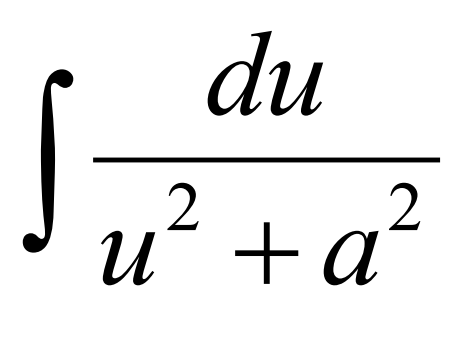
Integral of (see photo)

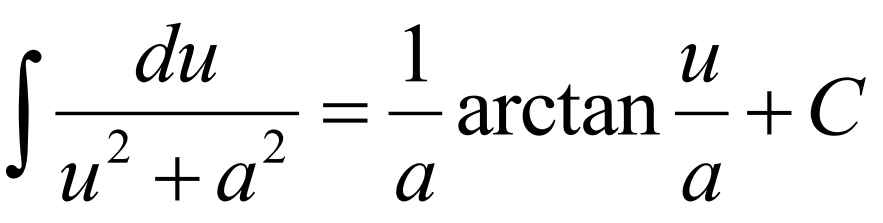
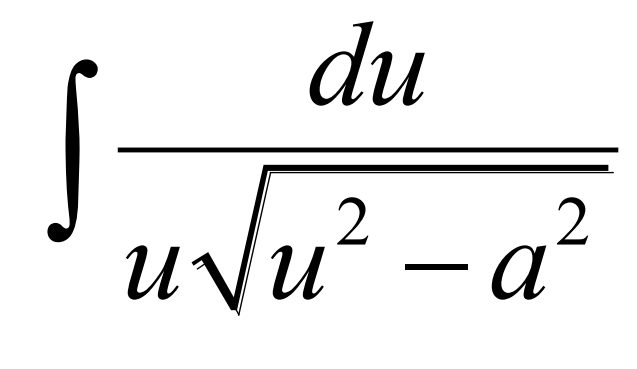
Integral of.. (see photo)

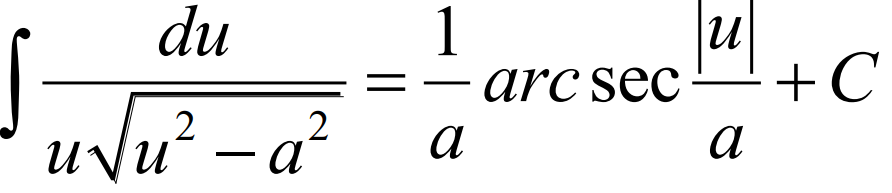
Right and left Riemann sum

Width- x or the top of the table

Length- y or the bottom of the table

Formula: (Width) (Length) + (Width) (Length) +…

1) Make your subintervals

2) Find width of first subinterval: Left X Value - Right X Value

3) Multiply by length (Right: Length will be the right y value of THAT subinterval. Left: Length will be the left y value of THAT subinterval.

4) Repeat for other subintervals

5) Add subintervals together

Midpoint Riemann sum

Width- x or the top of the table

Length- y or the bottom of the table

Formula: (Width) (Length) + (Width) (Length) +…

1) Make your subintervals

2) Find width of subinterval: Left MOST X value of subinterval - right MOST X value of subinterval (Ignore middle value)

3) Multiply by length (Length will be the middle Y value of subinterval)

4) Repeat for other subintervals

5) Add subintervals together

Trapezoidal Riemann Sum

Height- X or top of the table

Bases- Y or bottom of the table

Formula: ½ [(base₁ + base₂) x height]

1) Make your subintervals

2) Add bases of that subinterval together (Y-values)

3) Multiply sum of bases to the height of the subinterval (To find height: Left x value of subinterval - right x value of subinterval)

4) Do the same for the other subintervals

5) Add subintervals together

6) Multiply answer by ½

Definition of a Critical Number

Let f be defined at c. If f'(c) = 0 or if f'(c) is undefined at c, then c is a critical number of f.

First Derivative Test

If f' changes from negative to positive at c, then f(c) is a relative minimum of f. If f' changes from positive to negative at c, then f(c) is a relative maximum of f.

Second Derivative Test

If f'(c) = 0 and f''(c) > 0, then f(c) is a relative minimum. If f'(c) = 0 and f''(c) < 0, then f(c) is a relative maximum.

Definition of Concavity

The graph of f is concave upward on I if f' is increasing on the interval and concave downward on I if f' is decreasing on the interval.

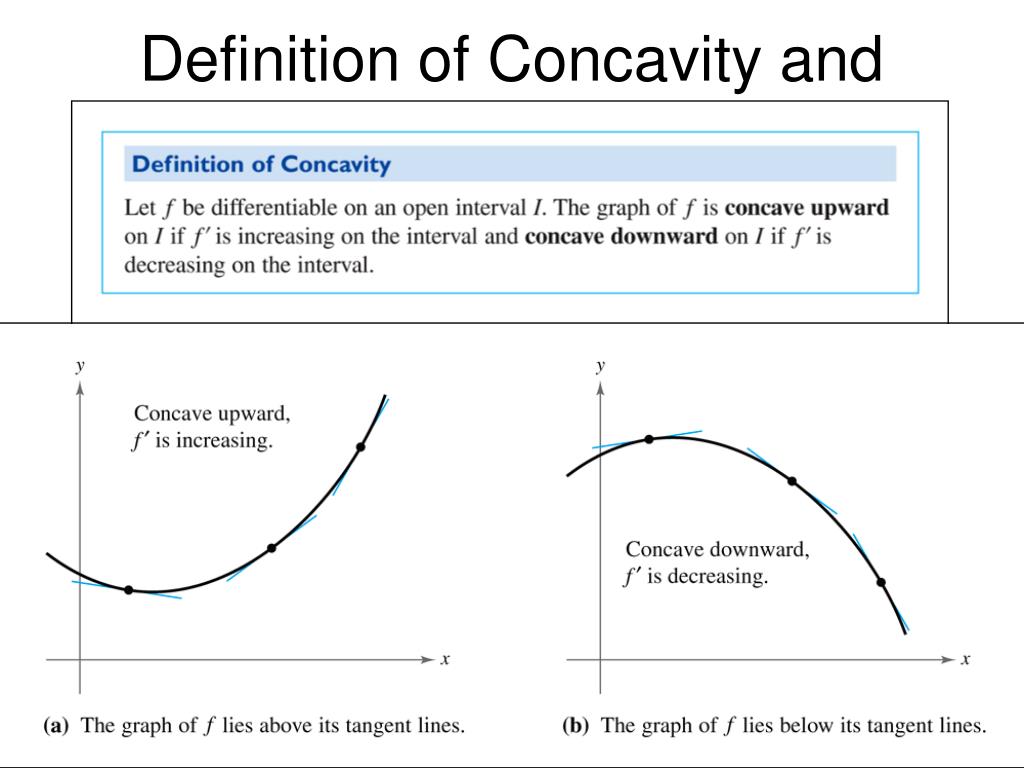
Test for Concavity

If f''(x) > 0 for all x in I, then the graph of f is concave upward in I. If f''(x) < 0 for all x in I, then the graph of f is concave downward in I.

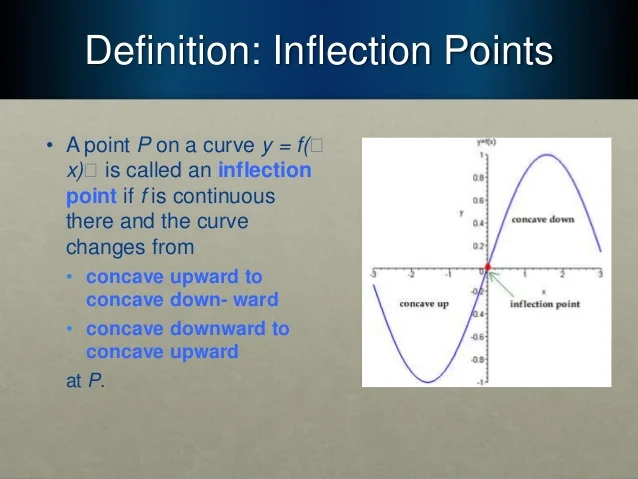
Definition of an Inflection Point

A function f has an inflection point at (c, f(c)) if f''(c) = 0 or f''(c) does not exist and if f'' changes sign from positive to negative or negative to positive at x = c OR if f' changes from increasing to decreasing or decreasing to increasing at x = c.

First Fundamental Theorem of Calculus

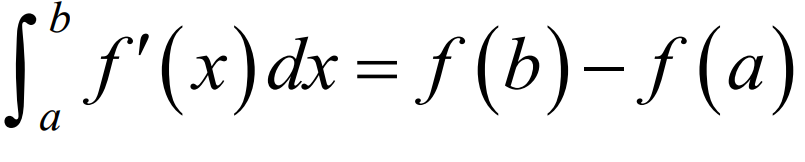
Second Fundamental Theorem of Calculus

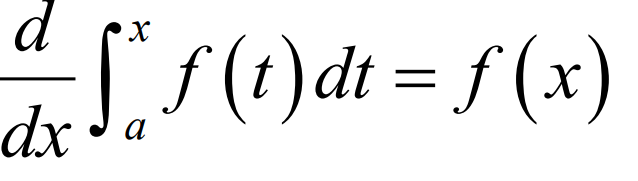
Second Fundamental Theorem of Calculus (Chain Rule Version)

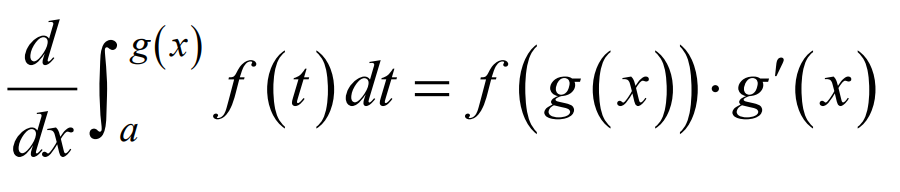
Average value of f(x) on [a, b]

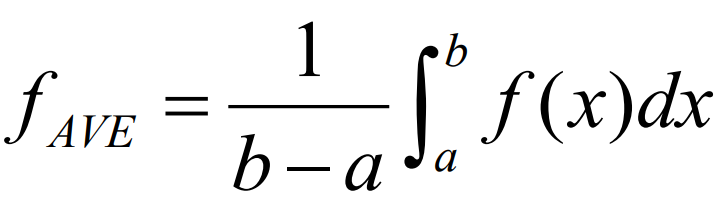
Disk method rotating around the x and y axis formulas

Washers method rotating around the x and y axis formulas

Horizontal (x-axis)~ Right - Left

Vertical (y-axis) ~ Top - Bottom

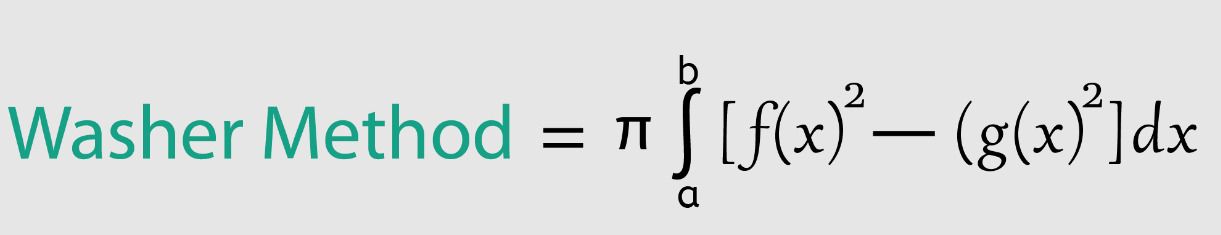
Volume by cross sections taken perpendicular to the x-axis

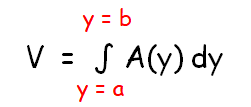
Velocity

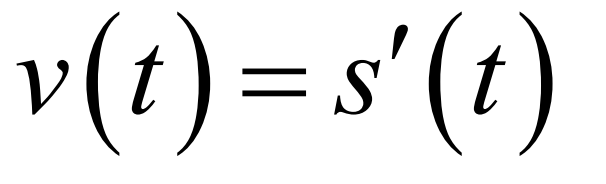
Speed

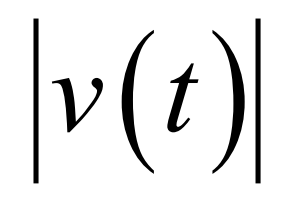
Acceleration

Displacement

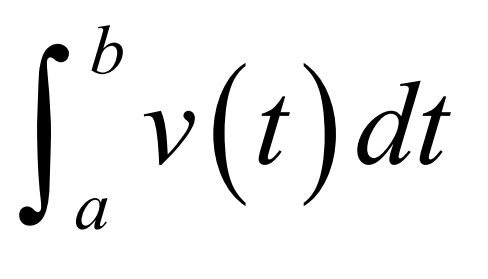
Total Distance

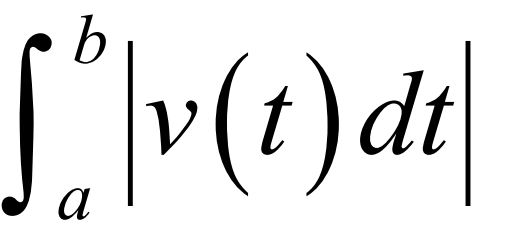
Total distance with two graphs

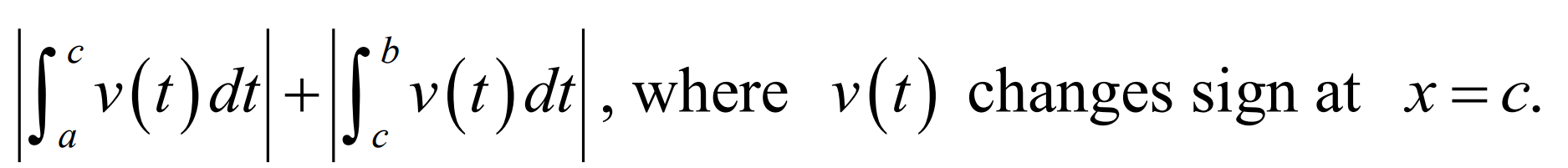
Differential equation for logistic growth (BC TOPIC ONLY)

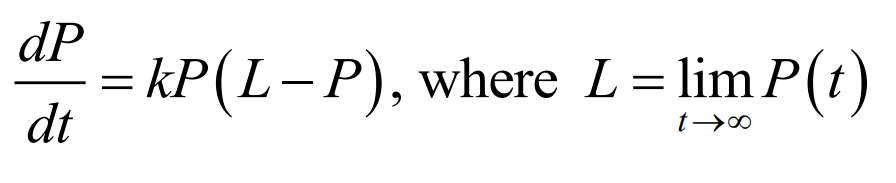
Integration by parts (BC TOPIC ONLY)

Two things being multiplied by eachother

Tabular’s method (L.I.A.T.E)

L- Logarithmic functions

I- Inverse trig

A- Algebra

T- Trig

E- Exponential

Arc Length (BC TOPIC ONLY)

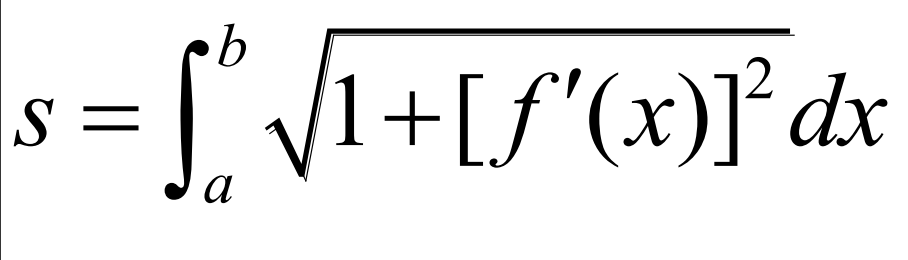
Position vector (BC TOPIC ONLY)

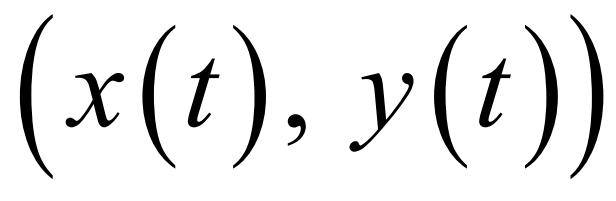
Velocity vector (BC TOPIC ONLY)

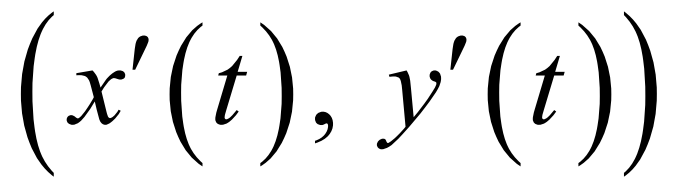
Acceleration vector (BC TOPIC ONLY)

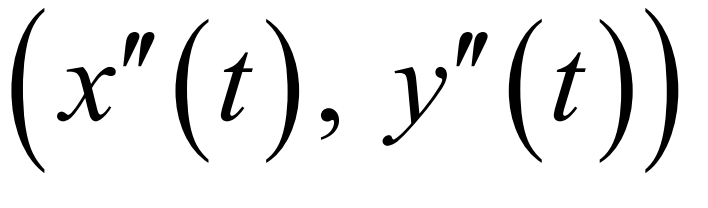
Speed (Or magnitude of a velocity vector) (BC TOPIC ONLY)

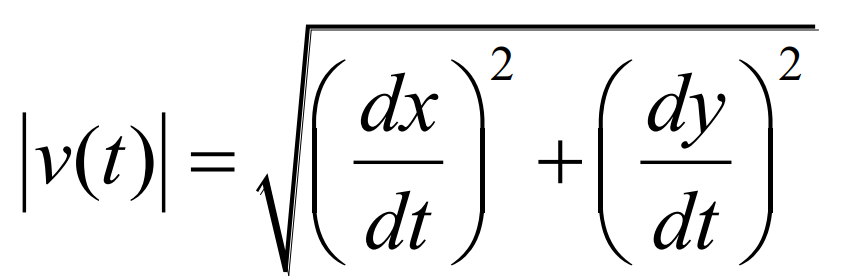
Distance traveled (Also known as arc length) (BC TOPIC ONLY)

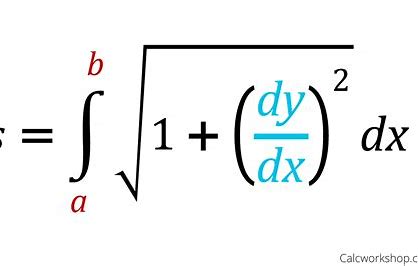
Polar curve coordinates (BC TOPIC ONLY)

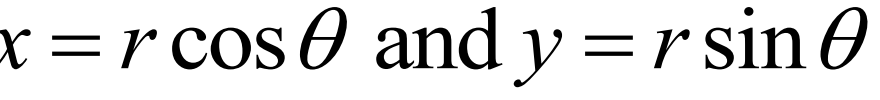
Slope of a polar curve (BC TOPIC ONLY)

Plug in values but don’t simplify if an FRQ

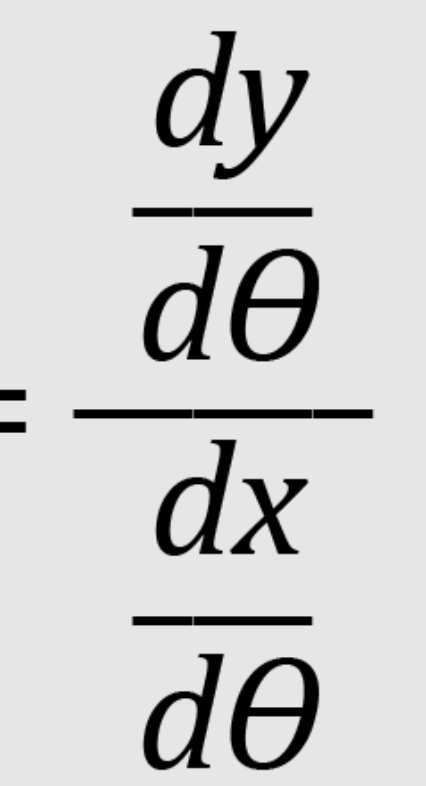
Area inside a polar curve (BC TOPIC ONLY)

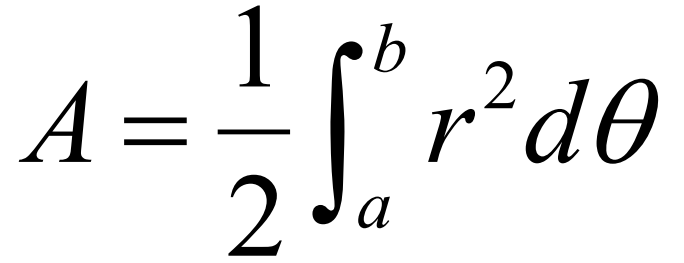
Speed for a polar curve (if given velocity) (BC TOPIC ONLY)

√(y’(t))² + (x’(t))²

Total distance for a polar curve (if given velocity) (BC TOPIC ONLY)

∫^b_a √(x’(t))² + (y’(t))²

Taylor Series polynomial (BC TOPIC ONLY)

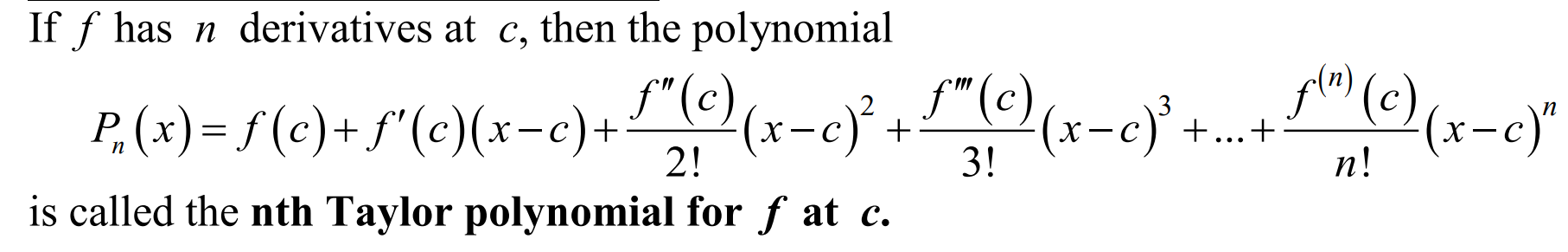
Lagrange Error Bound / Taylor's Theorem Remainder (BC TOPIC ONLY)

Alternating Series Remainder (BC TOPIC ONLY)

Maclaurin series of e^x (BC TOPIC ONLY)

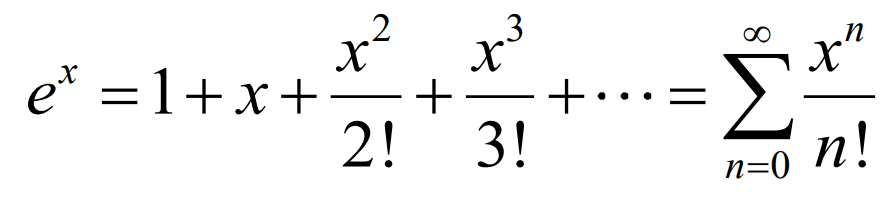
Maclaurin series of cos(x) (BC TOPIC ONLY)

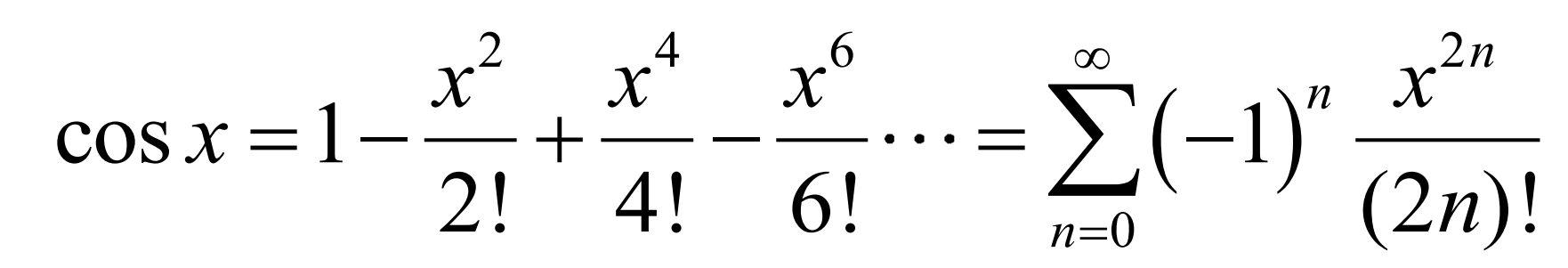
Maclaurin series of sin(x) (BC TOPIC ONLY)

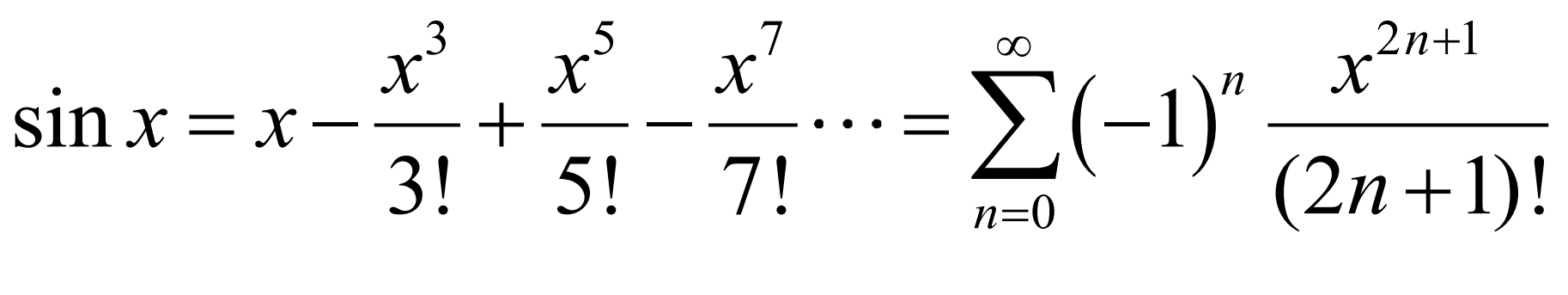
Nth- Term test (BC TOPIC ONLY)

(Series formula, condition for convergence?, condition for divergence?)

Geometric series test (BC TOPIC ONLY)

(Series formula, condition for convergence?, condition for divergence?)

p-Series test (BC TOPIC ONLY)

(Series formula, condition for convergence?, condition for divergence?)

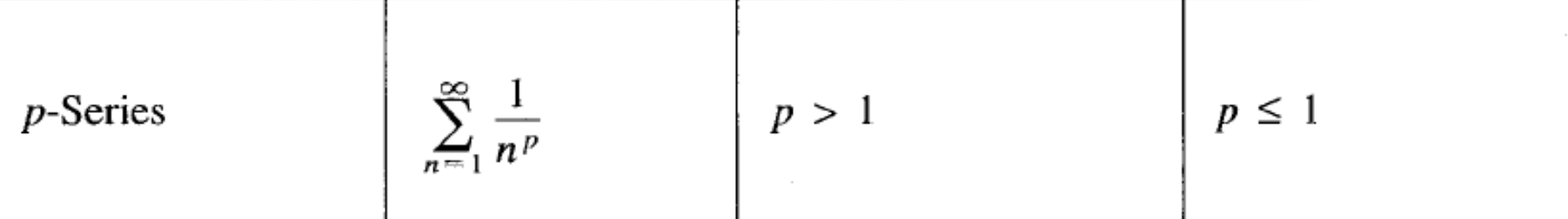
Alternating series test (BC TOPIC ONLY)

(Series formula, condition for convergence?, condition for divergence?)

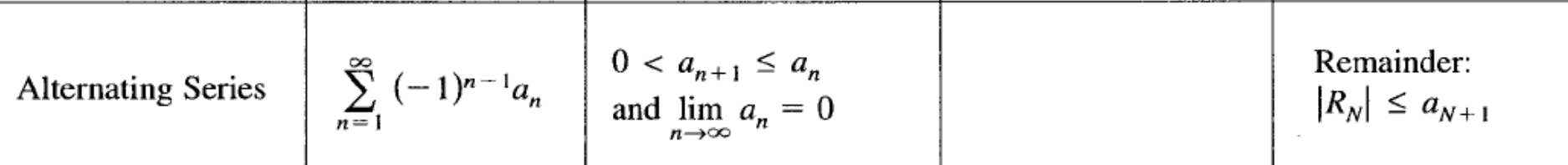
Integral test (BC TOPIC ONLY)

(Series formula, condition for convergence?, condition for divergence? What are the 3 conditions needed to use this test?)

Continuous?

Positive?

Decreasing?

Root test (BC TOPIC ONLY)

(Series formula, condition for convergence?, condition for divergence?)

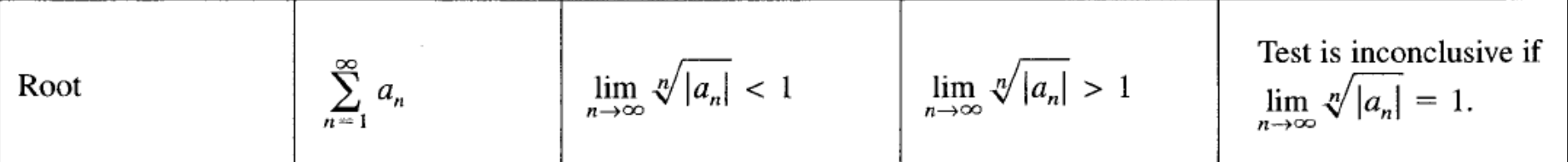
Ratio test (BC TOPIC ONLY)

(Series formula, condition for convergence?, condition for divergence?)

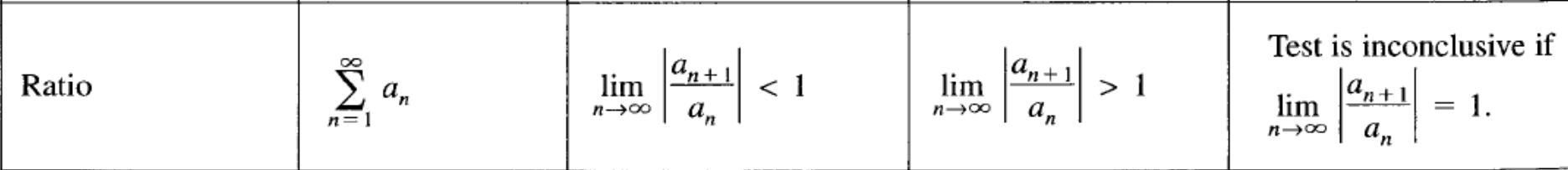
Direct Comparison test (BC TOPIC ONLY)

(Series formula, condition for convergence?, condition for divergence?)

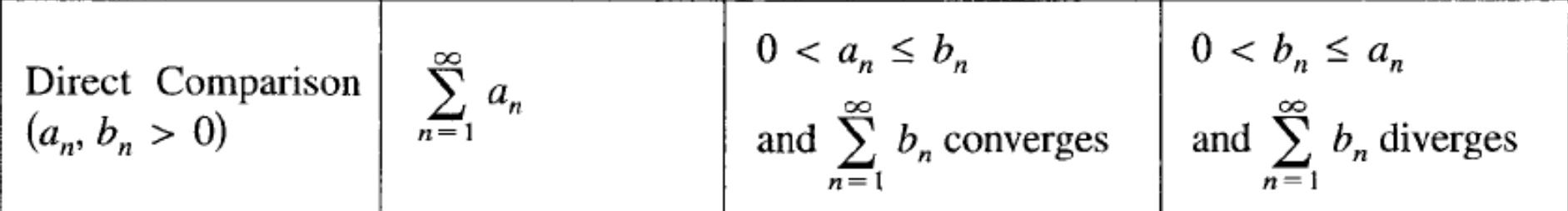
Limit Comparison test (BC TOPIC ONLY)

(Series formula, condition for convergence?, condition for divergence?)