Proof

Define a statement

Declarative sentence that is either true or false but not both

Can check if a sentence is a statement by adding “Is it true that” before it, and see if it makes sense

Define an axiom

Statement agreed to be true, e.g. commutative law a + b = b + a

Define definition

Precise statement of the meaning of a mathematical word, don’t require proof (e.g. an even number = 2n)

Define a theorem

Describes the relationship between two or more mathematical ideas, using axioms and/or definitions. E.g. quadratic formula

What is the key difference between axioms and theorems

Theorems require proof, they start as a proposition

Define lemma

A minor, proven statement used to help prove a larger theorem

What is a corollary

Theorem of less importance which is deduced after proving another theorem

Define a predicate

Sentence containing one or more variables that becomes a statement if we know the values of the variables

(If you can’t say it’s true/false it’s a predicate)

Maps domain of discourse to true or false

What is the domain of discourse

The values a variable in a predicate can take

Come back to if Pn Q , P V Q is statement or predicate

What is a tautology

A predicate whose truth value is always true, whatever the value of the variables (truth table true for whole column)

What are mathematical arguments made from

Premises and a conclusion

Define a premise

A statement used as evidence in an argument, intended to be true

What is a conclusion

Statement that follows logically from the premises

What does it mean for an argument to be:

a) valid

b) sound

a) Conclusion follows logically from the premises, regardless if the premises are true

b) Valid and all premises true

What are the two key tautology examples

Modus ponens and Modus Tollens

What is modus ponens

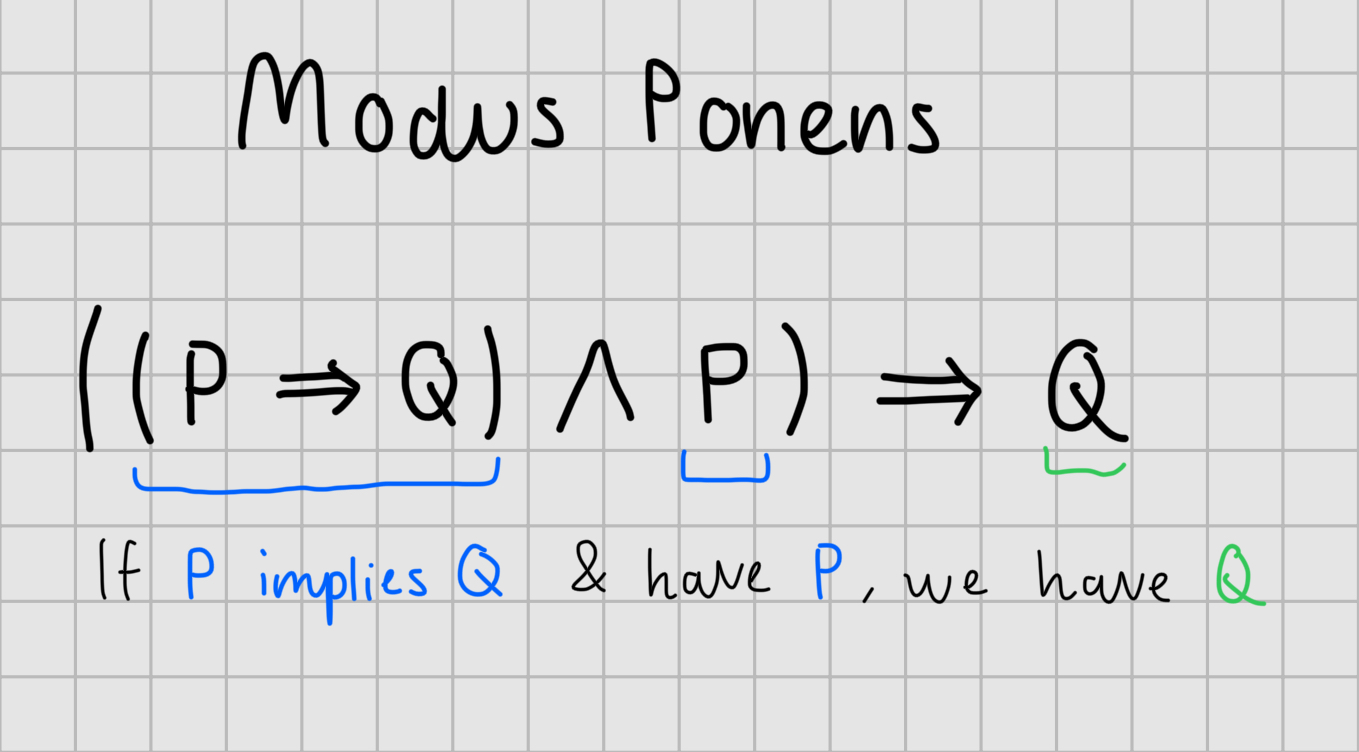
Give a mathematical example of Modus Ponens

This argument is sound, valid and premises true

What is Modus Tollens

Once again always valid, even though premises may not be true

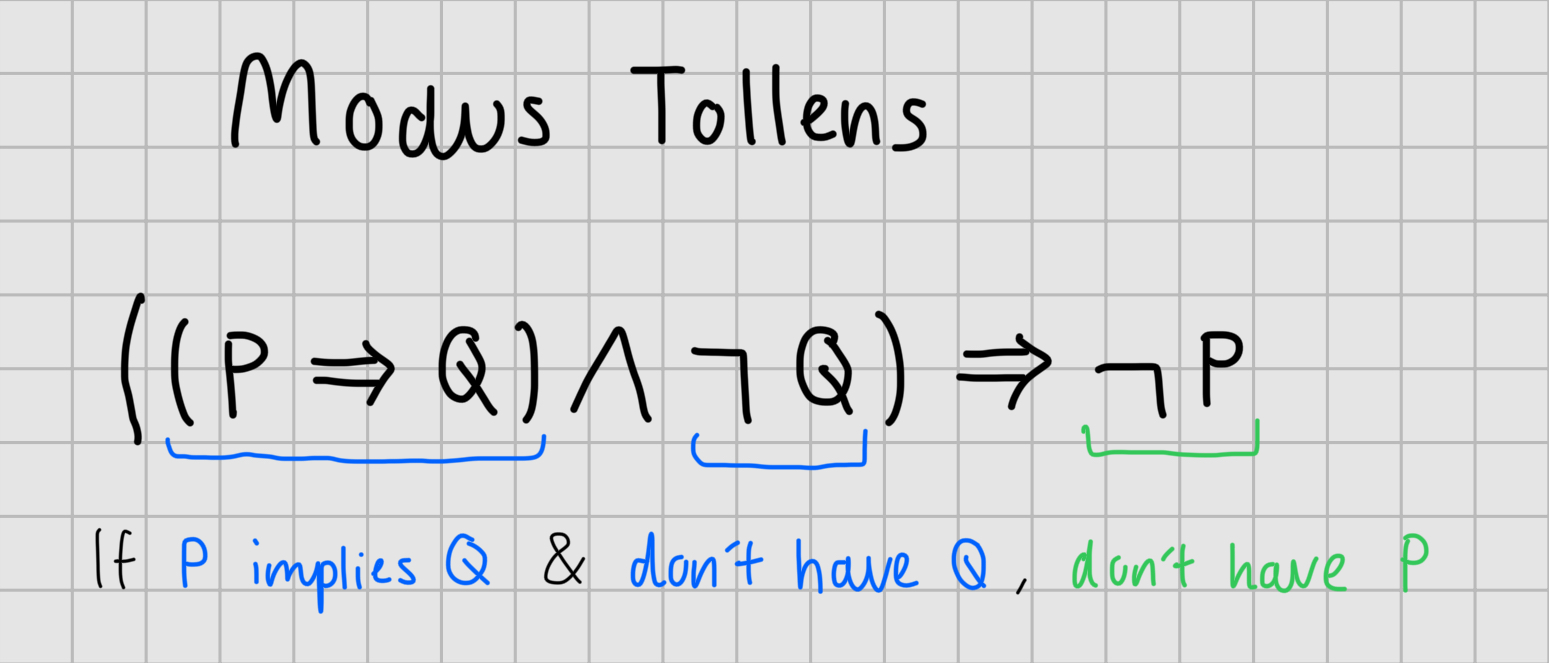
What can be said about all arguments that follow Modus ponens or Modus Tollens

Always valid, not always sound

What is the contrapositive of P implies Q ( P → Q)

Not Q → Not P

When are two statements logically equivalent

When P ←→ Q

What can be said about th contrapositive

A statement and its contrapositive are logically equivalent ( P ←→ Q)

Give an example of how a new predicate can be formed from Q(x, y, z)

New predicate’s only variable is x

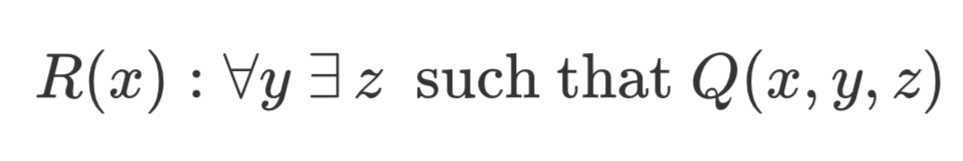
What rule from set theory can be applied to proof as a tautology

de Morgan’s laws

What tautologies are formed from de Morgan’s Laws

What tautologies involve the negative of quantifiers?

Why is it useful to negate statements involving quantifiers

Easier to prove “there exists an x…”, than to prove “that for all x…”

Therefore can negate statement with. “For all” and can check veracity of negation

Negate the following statement. Is the statement true? Is the negation true?

How would you prove a statement of the form A ← → B

1. Assume A is true, show A → B

2. Assume B is true, show B → A

Name all the types of direct or indirect proofs you can use

Direct:

1. Proof by deduction (simply showing P → Q)

2. Existence proof: constructive (example) and non constructive (showing some n does exist)

3. Counter example

4. Proof by exhaustion

Indirect:

1. Contradiction (show not P → Q, where Q is false, so P true)

2. Contrapositive ( not Q → not P)

What is the converse of the statement P implies Q

Q implies P

What is the contrapositive of the statement P → Q

Not Q → not P