pre calc everything

slope intercept form

point slope form

standard form

y=mx+b

y-y1=m(x-x1)

Ax+By=C

what points should you graph when graphing a quadratic

vertex

intercepts

how do you find axis of symmetry of a quadratic

-b/2a

end behavior

if leading coefficient is positive, as the graph approaches infinity, its positive

if the degree is even, as the graph approaches negative infinity it is the same. if it is negative, it is the opposite

how do you find vertical asymptote

set denominator equal to zero

(if the numerator is also zero, at the number it is equal to zero, it is a hole, not asymptote)

horizontal asymptote

Nx>Dx, none

Nx<Dx, y=0

Nx=Dx, y= ratio of leading coefficients

Nx is exactly 1 more than Dx, slant asymptote(found with long division, ignoring reminder)

draw the unit circle first quadrant

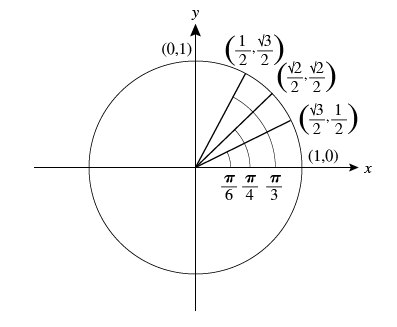
how do you find arc length

s = (θ/360) * πd

s= rθ

Arc length=s

r= radiusd

domain and range of trig functions

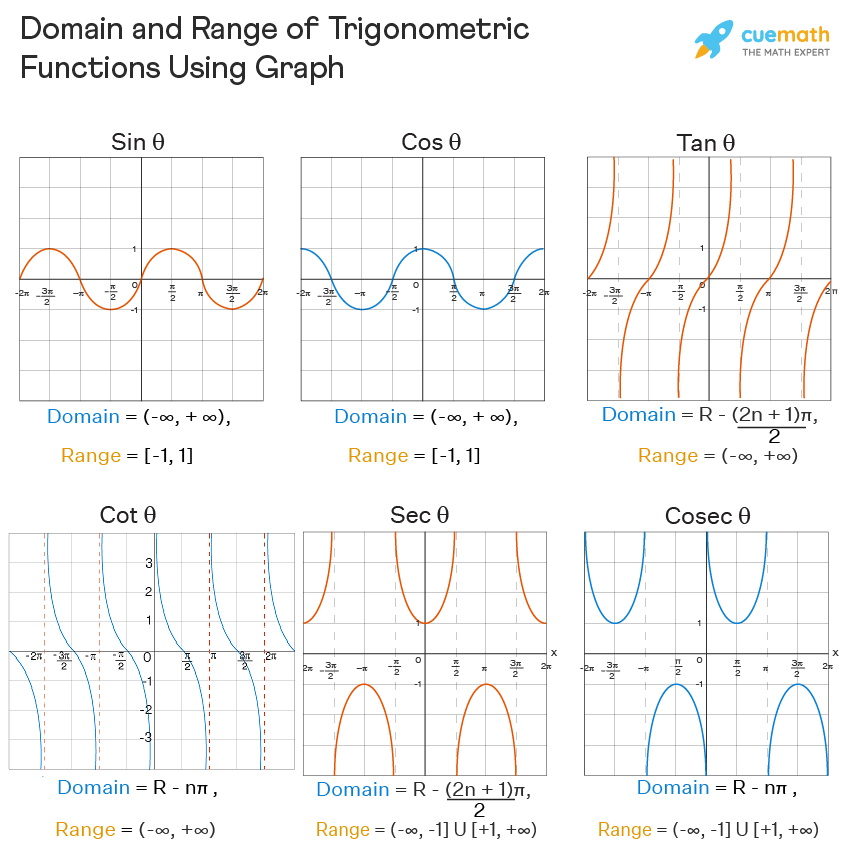
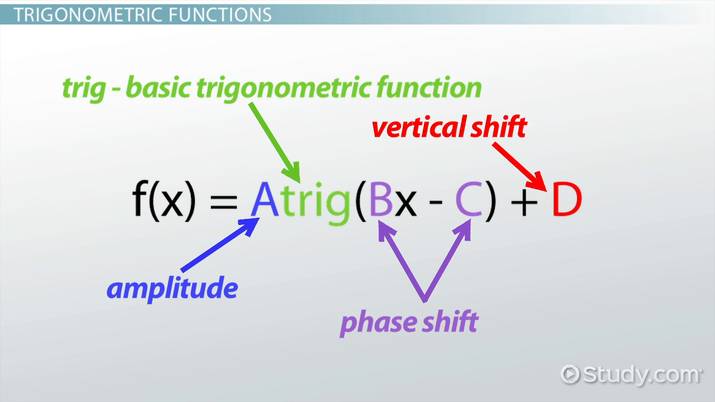
parts of trig function

Amplitude

period

v shift

scale

phase shift(C/B)

pythagorean Identity

sin²u+cos²u=1

1+tan²u=sec²u

1+cot²u=csc²u

Cofunction identity

relate the values of trigonometric functions for complementary angles (angles that add up to 90 degrees or π/2 radians)

sin(π/2-u)=cos u

tan(π/2-u)=cot u

sec(π/2-u)=csc u

cos(π/2-u)=sin u

cot(π/2-u)=tan u

csc(π/2-u)=sec u

even/odd identity

sin(-u)=-sin u

cos(-u)=cos u

tan(-u)=-tan u

csc(-u)=-csc u

sec(-u)=sec u

cot(-u)=-cot u

sum and difference formula

double angle formula

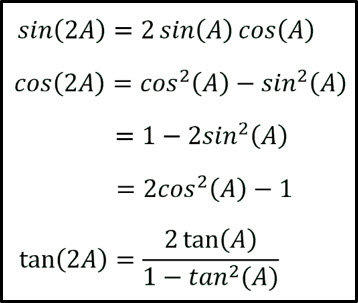
power reducing formula

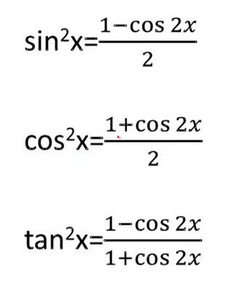
half angle formula

product to sum formula

sum to product

law of cosine

*find angle opposite the longest side first

area of a triangle formula

oblique triangle area

= ½ bcsinA

= ½ acsinB

= ½ absinC

Heron’s Area formula

s= (a+b+c)/2

area = √(s(s-a)(s-b)(s-c))

criteria for solving an oblique triangle

use law of sine for

AAS or ASA(results in unique triangle

SSA (can have no such triangle, two distinct triangle, one distinct triangle)

use law of cosine for

SSS

SAS

how do you find the magnitude of a directed line segment

distance formula

d = √((x₂ - x₁)² + (y₂ - y₁)²)

||v||=√(v1)²+(v2)²

what is standard position of a directed line segment

initial point is the origin

component form of vector with initial point P(p1,p2) and terminal point Q(q1,q2)

→PQ=<q1-p1,q2-p2>=<v1,v2>

initial point is at (0,0)

unit vector formula

magnitude of 1

v→/ ||v||

v→=vector

||v→||= magnitude

ex.

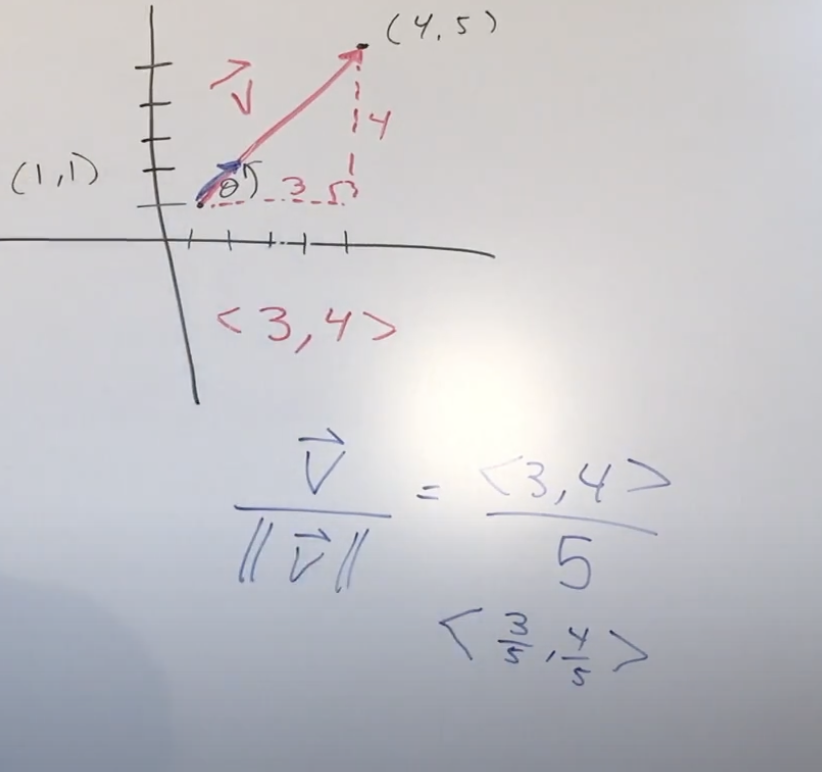
standard unit vectors

i=<1,0>

j=<0,1>

horizontal and vertical components of v

dot product

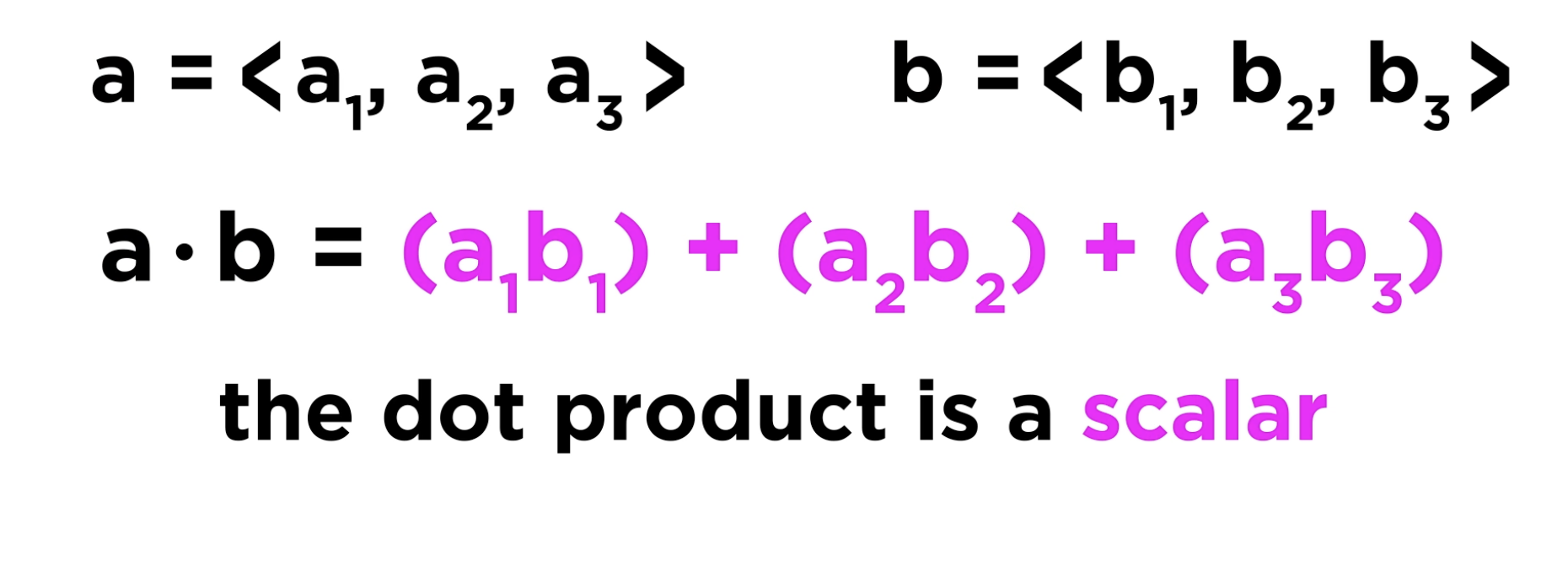
how do you find the angle between 2 nonzero vectors using dot product

the angle is between 0 and pi

denominator is magnitude

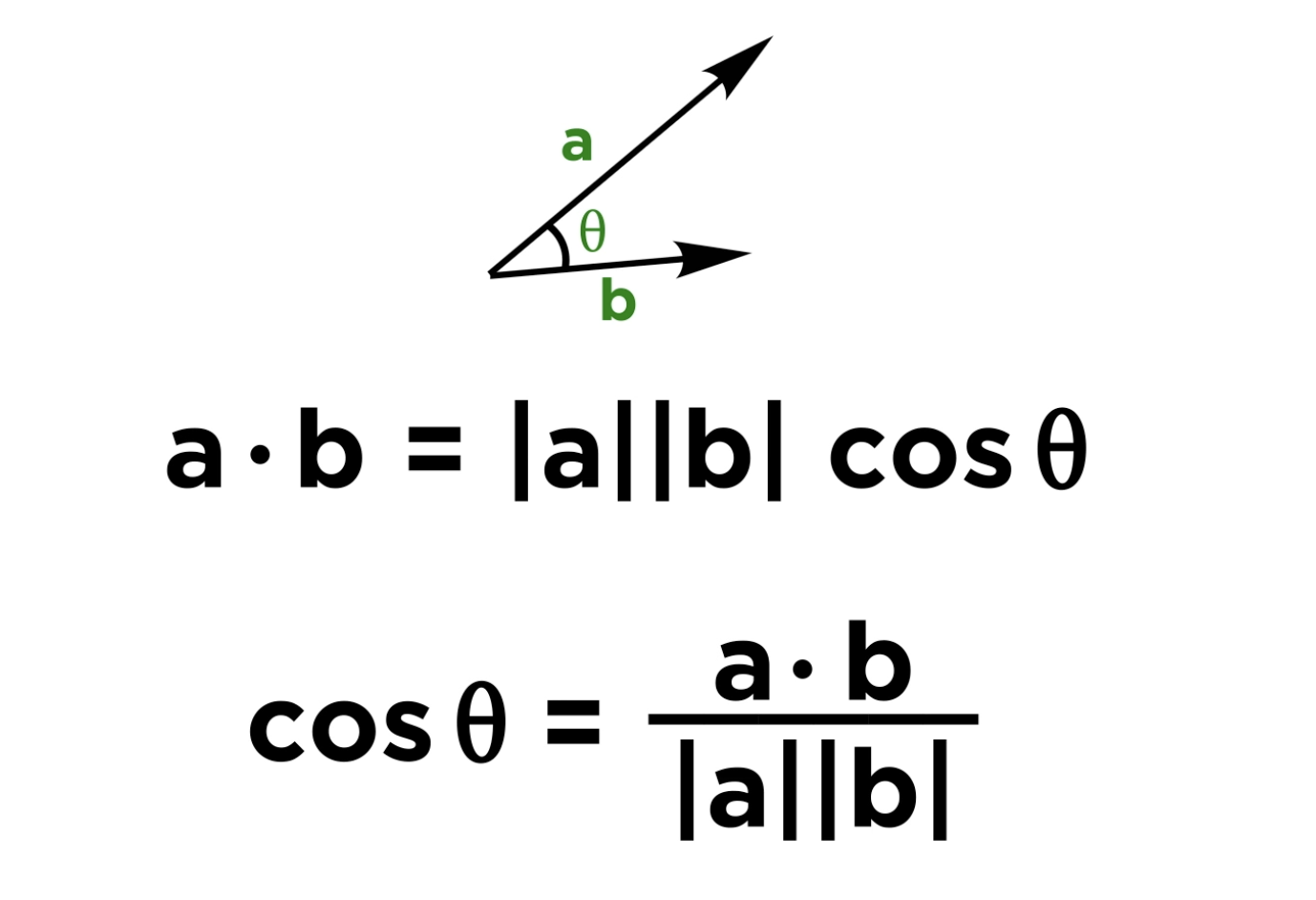
orthogonal

when dot product of a and b equals 0

a*b=0

the vectors form a 90º angle

0 vector is orthogonal to every vector

how to find the direction angle of a vector

θ=tan^-1 (y/x)

tanθ=(y/x)

angle is measured clockwise from positive x-axis

remember to draw the vector because calc may give wrong answer because tangent inverse is restricted from pi/2 and -pi/2 or -90º to 90º

parabola equation

vertex form

y = a(x - h)² + k

standard form

y = ax² + bx + c

equation of a circle

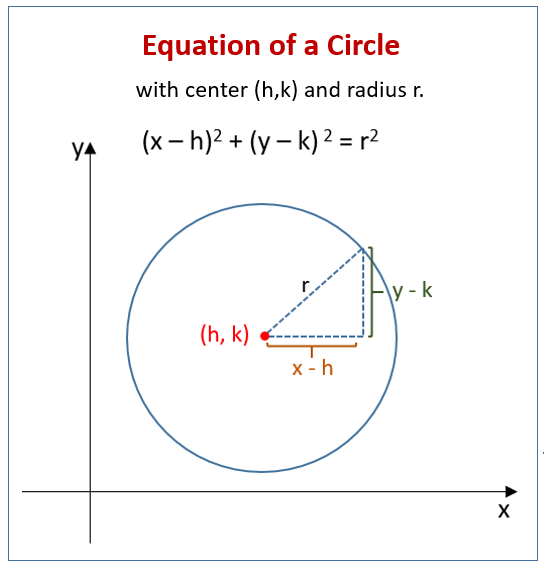
how do you find the focus and directrix of a parabola

p= distance from vertex to focus = distance from vertex to directrix

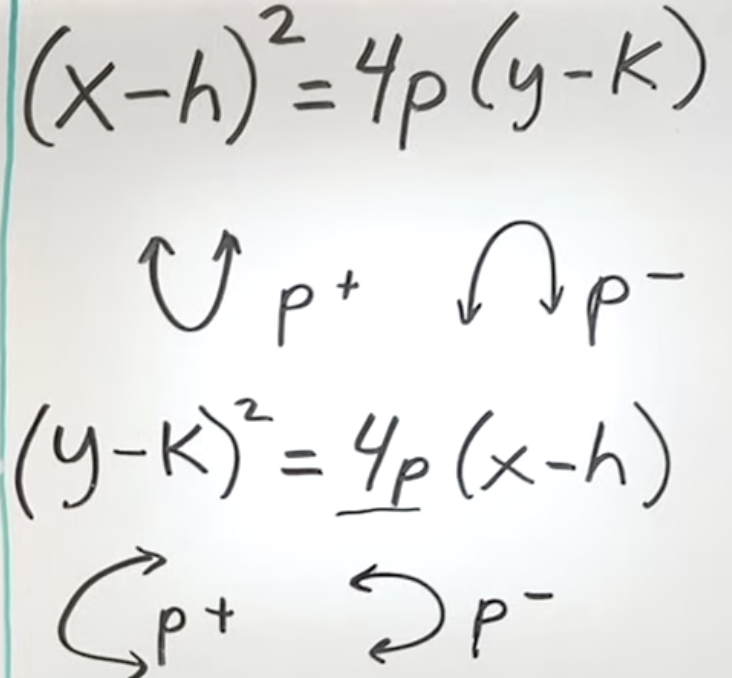
ellipse formula and graph

c is distance from center to focus

c²=a²-b²

e is eccentricity (how round)

e=c/a 0<e<1 closer to 0 is closer to a circle

a² is the larger denominator

if a is under y, its longer in the y axis,

if it is under x, its longer in the x axis

• vertices are found by adding a and b values to the center

• end points of major axis are called vertices

• endpoints of minor axis are the co-vertices

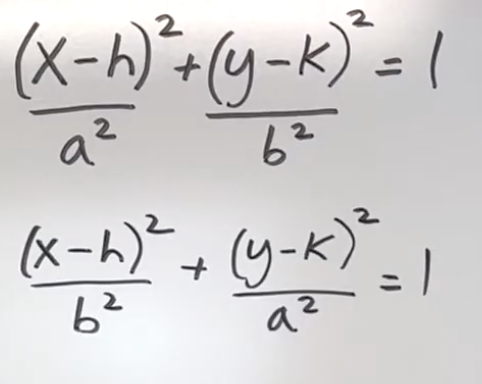
summation notation(sigma notation) and example

I=index of summation (does not have to be i)

n=upper limit of summation

1= lower limit of summation(doesn’t have to be 1)

series

sum of terms in a finite OR infinite sequence

finite series or partial sum and notation

sum of first n terms of a sequence

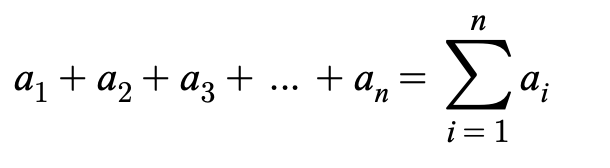
infinite series and notation

sum of all terms of an infinite sequence

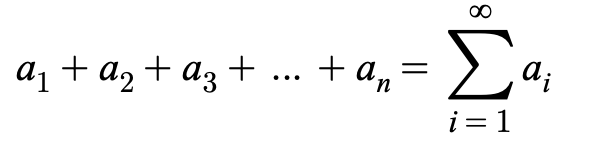
arithmic sequence

a sequence with a common difference

a_n=a₁+(n-1)d

d=common difference

a1= first term of the sequence

sum of a finite arithmetic sequence

S_n=n/2(a₁+a_n)

Sn=sum of a finite arithmetic sequence with n terms

geometric sequence

terms have a common ratio, r

r= a₂/a₁=a₃/a₂=a₄/a₃=…

a_n=a₁r^n-1

sum of finite geometric sequence when cannon ration is not 1

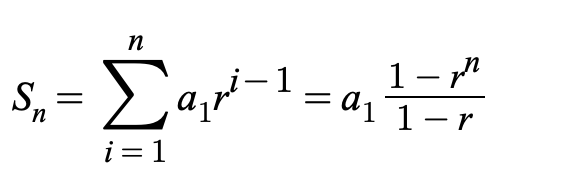
infinite geometric series or geometric series

if |r|<1, then the infinite geometric series has the sum

(picture)

if |r| ≥ 1, the series does not have a sum

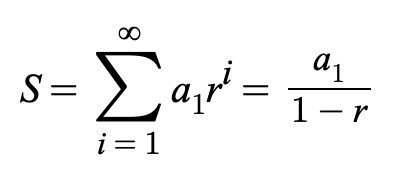
permutation

ordering of elements

number of permutations of n elements is given by

n(n-1)…4×3×2×1=n! (there are n! ways for n elements to be ordered

the number of permutations of n elements taken r at a time

_nP_r=n!/(n-r)!

n=number of elements

r=how many of the elements are taken at a time

distinguishable permutations

n! / n₁!*n₂!*n₃!…n_k!

ex.

banana’s letters can be arranged 60 ways

6 letters

3 a

2n

1b

6! / 3!*2!*1! =60

combinations

order of elements does not matter

number of combinations of n elements taken r at a time is given by

_nC_r= n! / (n-r)!r!

when does the limit not exist

• when the left and right behavior don’t agree ex. one is negative, the other is positive

• when f(x) increases or decreases without bounds

• oscillating behavior between tow fixed values

what do you do when you get the indeterminate for when finding the limit

0/0 can be obtained with direct substitution, in that case, rationalize by multiplying both the numerator and the denominator by the conjugate of the numerator

derivative

derives the slope of the graph of f at a point (x,f(x))

denoted f’(x) “f prime of x”

or dy/dx, y’, d/dx[f(x)], and D_x[y]

f’(x) = lim_h→0 (f(x+h) - f(x)) / h

ex.

f(x) = 3x²-2x

= 6x-2

h=change in x / change in y

right side of the equation is called difference quotient

only works if the limit exists

what is the derivative of a constant

0