N8: calculate exactly with fractions, surds and multiples of π; simplify surd expressions involving squares (e.g. √12 = √(4 × 3) = √4 × √3 = 2√3) and rationalise denominators

What is a surd?

Surds are the square roots (√) of numbers that cannot be simplified into a whole or rational number, also called irrational numbers

Is √4 a surd?

No because it can be simplified into ±2 - surds cannot be simplified into whole numbers

What is good about a surd?

Surds are the exact value - if it was converted into a regular number, it wouldn’t be exact

What is rationalising?

Removing any surds from the denominator of a fraction

How to rationalise

If the denominator contains only a surd, multiply the whole fraction by that surd

If the denominator contains a surd and another number added or subtracted from it, multiply the fraction by that surd, number but with the opposite symbol (+ would become - and vice versa)

Rationalise (5-√3)/√2

Multiply the numerator by the surd (√2): (5-√3)√2=5√2-√6

Multiply the denominator by the surd (√2): √2²=2

Write the answer: (5√2-√6)/2

Rationalise √7/2+√7

2√7-7/-3

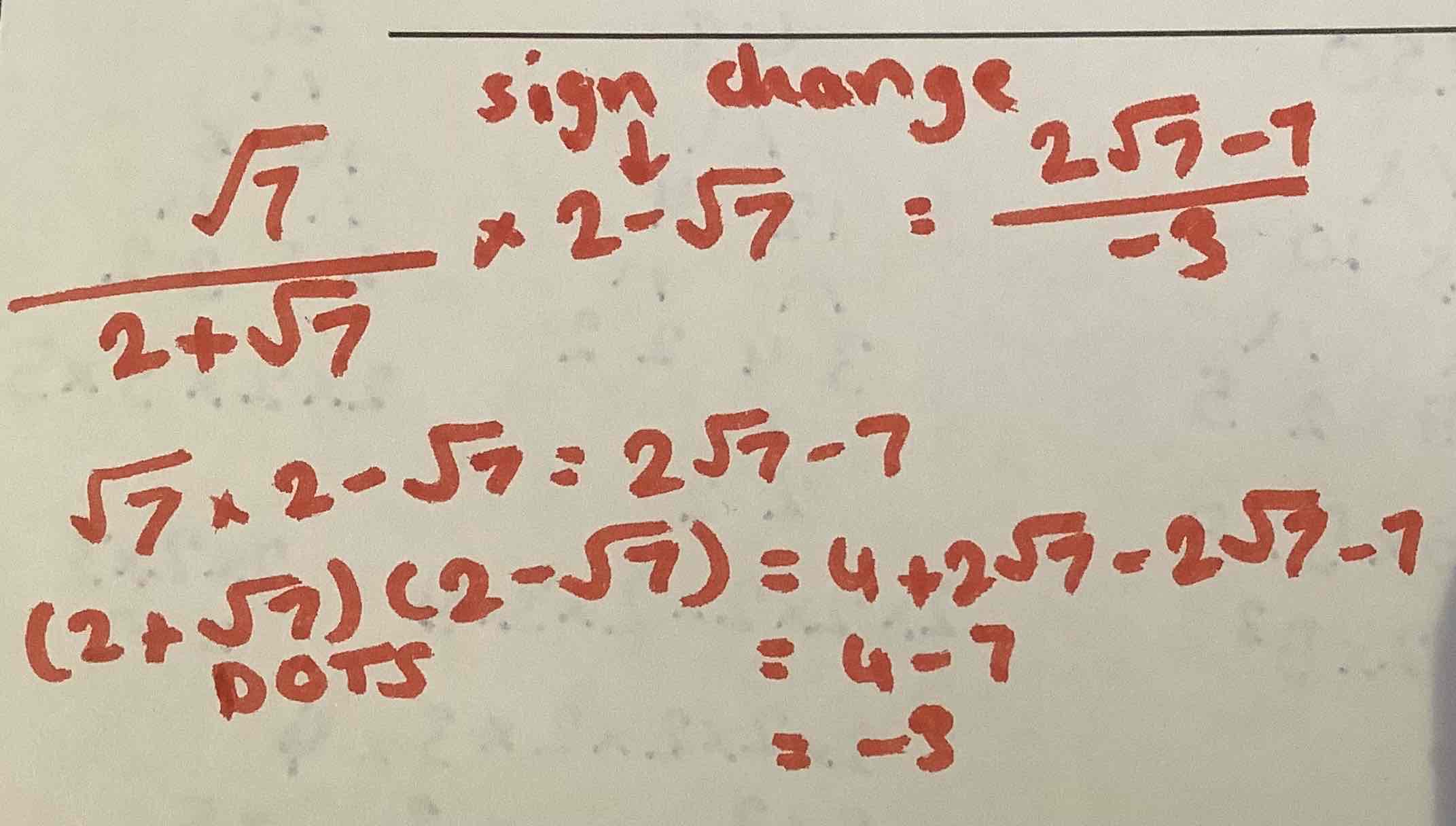
What is calculating with pi?

Similarly to a surd, pi represents an exact number with thousands of decimal places - in order to keep its exact value, we use the symbol 𝜋

How to calculate with 𝜋

When answering a question, keep the result in terms of 𝜋, such as 12𝜋 cm

Calculate the area of a circle with a radius of 3, leaving the answer in terms of 𝜋

Area of a circle = 𝜋r²

𝜋x3²=9𝜋

Answer=9𝜋 cm² (this is a more exact answer than 28.27)

How to simplify surds

1) Split the surd into a square number multiplied by another number

2) square root the number and take it outside of the square root

3) leave the other number unless it can be simplified further

Simplify √50

√50=√25x√2

√25=5

5√2

Simplfy 6√60

√60=√4x√15

2√15×6=12√15

12√15