6. Folk Theorems

What is a convex combination?

• Given vectors x, y, z ∈ Rⁿ, z is a convex combination of x and y if there exists a scalar α ∈ [0, 1] such that z = αx + (1 − α)y

• This means that z is an average of x and y and lies on the line segment between them

How do we define a convex hull?

• Given a set of vectors X = {x₁, x₂, . . . , x_k} in R_n , we define the convex hull of X as the smallest convex set containing X

• Co(X) ={x ∈ Rⁿ: ∃(α₁, . . . , α_k) ∈ R^k, ^k∑_j=1 α_j = 1, such that x = ^k∑_j=1 α_j x^j

• This essentially defines the smallest possible graphical space which includes all of the vectors

  • Every combination of different values (line segments between them) lies within or on the boundary of the set

• Extended to economics, this defines the set of all possible payoffs

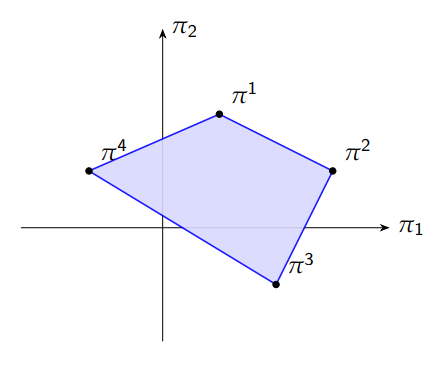
Feasible strategies

• Rely heavily on the discount rate, δ, being sufficiently high; if it is, then a sequence of action strategies (a^t)_t exists such that (1 − δ) ^∞∑ _t=0 δ^t u_i(a_t) = π_i

• As the discount rate gets sufficiently high, almost any feasible strategy above the Nash equilibrium could be sustained by players alternating strategies in different periods (being willing to have a bad period followed by a good period for greater average payoffs)

• These strategies can’t exist unless the discount rate is sufficiently high; when a person is patient enough, we can recognise that their long-run average discounted payoff is π_i

How does Nash reversion work?

• To incentivise another player to cooperate, we threaten them with punishment; reversion to a Nash equilibrium

• To ensure the maximum punishment, we want to choose the Nash equilibrium which gives them the minimum payoff: w_i^NE = min π_i(s*), where s* is a Nash equilibrium

What is the Friedman Folk Theorem?

• For each feasible payoff vector π ∈ F such that π_i > w_i^NE for all i ∈ N, there exists a discount factor δ^x such that π is the SPNE (average) payoff of the infinite repeated game for any discount factor greater than δ^x

• To simplify, for every payoff which is feasible and affords every player a payoff greater than Nash reversion, there is a threshold discount factor such that, if the discount factor is above it, then these payoffs can be sustained as SPNE

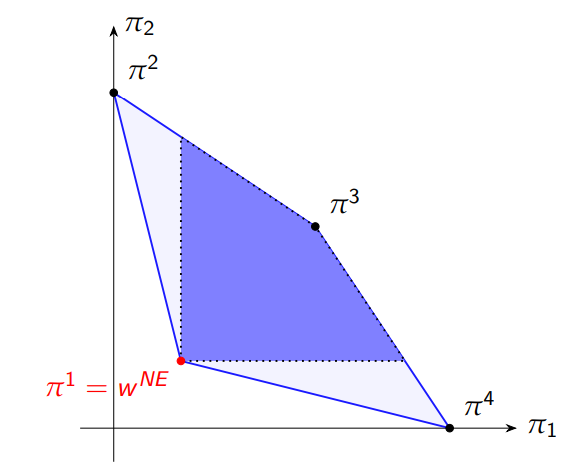
How is Friedman’s Folk Theorem constructed?

• Fix π ∈ F

• Construct a sequence of actions (a_i^(t))_t that generate payoff vector v

• If a player deviates, the upper bound on payoffs is max_ai u(a_i , a_−i) = u^x in the current stage and w^NE forever after, which amounts to (1 − δ)u_i^x + δw_i^NE

• Although π_i > w^NE , there exists δ_i such that π_i = (1 − δ)u_i^x + δw_i^NE

• Set δ^x = max_i δ_i

• Thus this punishment only works if the player is patient enough such that δ > δ^x incentivises cooperation

How might players use a minmax vector to punish more harshly?

• If a player is playing myopically p_m, and thus only best responds in the stage game and doesn’t care about future consequences, the other players in the game - if hostile - will choose the worst environment for the myopic player to best respond to

• Thus, the strategy profiles which p_m can best respond to are minimised, and the response p_m chooses towards these profiles is maximised, hence, the minmax vector

• w˜ = min_{σ−i∈Πj̸=i∆Sj} max_ai π(a_i , σ_−i)

• In any SPNE, every player achieves a payoff weakly greater than the minmax payoff, which we call individually rational

What is the Fudenberg Maskin Folk Theorem?

• For each feasible payoff vector π ∈ F such that π_i > w˜_i for all i ∈ N, there exists a discount factor δ¯ such that π is the SPNE (average) payoff of the infinite repeated game for any discount factor greater than δ¯

• Essentially the same as Friedman’s folk theorem, but it changes w^NE for w^~, it changes the payoff of Nash Reversion to the payoff of the minmax vector

• Again, if a person is patient enough, such that δ > δ¯, then a payoff can be sustained which is greater than the minmax vector

• The minmax payoff vector includes mixed strategies

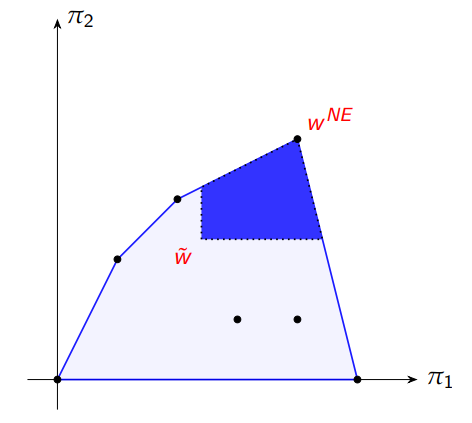
Why is the Fudenberg Maskin Folk Theorem more useful than Friedman’s?

• It extends the set of feasible payoffs which can be supported; Friedman’s theorem argues only payoffs greater than w^NE can be supported but if NE is high, there might not be any payoffs above it

• w^~ allows for harsher deviation punishments because w^~ < w^NE

• Minmax allows for boundary results (payoffs equal to minmax)

• Friedman uses Grim Trigger as the basis which is unrealistic, whereas Fudenberg-Maskin allows for cooperation after deviation thus is more adaptable to changes and is realistic

• Where Friedman only provides the existence of some payoffs, Fudenberg-Maskin characterise the entire set of payoffs available

Friedman vs Fudenberg-Maskin Folk Theorem Summary Table