I. Fondamentaux sur les matrices (suite)

Qu’est-ce que le polynôme caractéristique d’une matrice ?

1.1 Définition

Soit A une matrice carrée de M(n,n). On appelle polynôme caractéristique et on note P_A(λ) le polynôme défini par

P_A(λ) = det(A − λId)

Combien de racines admet un polynôme de degré n ? Comment s’appellent ces racines?

Ce polynôme de degré n admet n racines complexes appelées valeurs propres.

Comment est appelé la multiplicité d’une racine ?

La multiplicité d’une racine est appelée multiplicité algébrique de la valeur propre.

Qu’est-ce qu’un vecteur propre ?

On appelle vecteur propre x associé à la valeur propre λ un vecteur non nul vérifiant Ax = λx

Qu’est-ce qu’un rayon spectrale ?

Qu’est-ce qu’un sous-espace propre et une multiplicité géométrique ?

1.2 Définition

On appelle sous espace propre associé à la valeur propre λ l’e.v. défini par E(λ) = Ker(A − λId).

On appelle multiplicité géométrique de λ la dimension du sous espace propre associé.

Qu’affirme la proposition sur les multiplicités ?

1.3 Proposition (admis)

La multiplicité algébrique est supérieure ou égale à la multiplicité géométrique.

Quels liens existent entre les vecteurs associés à deux espaces propres distincts?

1.4 Proposition

Soient x ∈ E(λ) et y ∈ E(μ) où λ ≠ μ. Les vecteurs propres x et y sont linéairement indépendants.

Qu’est-ce qu’une matrice diagonalisable ?

1.5 Définition

On dit qu’une matrice A est diagonalisable ssi il existe une matrice inversible P t.q. A = PDP⁻¹ où D est diagonale.

Quelle condition caractérise les matrices diagonalisables ?

1.6 Proposition (admis)

A est diagonalisable ssi la multiplicité géométrique est égale à multiplicité algébrique pour toutes les valeurs propres. De plus D est formé des valeurs propres de A.

Quel résultat énonce la factorisation de Schur ? Toute matrice A est……….. dans une ………………, i.e. il existe U une matrice …………et T une matrice ……………….t.q…………...

1.7 Théorème (Factorisation de Schur, admis)

Toute matrice A est triangularisable dans une base orthonormale, i.e. il existe U une matrice unitaire et T une matrice triangulaire supérieure t.q. A = UTU*.

Quel est le théorème de diagonalisation dans une base orthonormale ?

1.8 Théorème (Diagonalisation base orthonormale)

Une matrice A est diagonalisable dans une base orthonormale ssi elle est normale :
A = UDU* ⇔ AA* = A*A.

Quelle est la proposition (cf TD) sur les matrices hermitiennes ?

Qu’est-ce qu’un polynôme appliqué à une matrice ?

Qu’affirme la proposition concernant les valeurs propres ?

1.11 Proposition

Si λ est valeur propre de A, alors P(λ) est valeur propre de P(A).

Quel résultat établit le théorème de Cayley–Hamilton ?

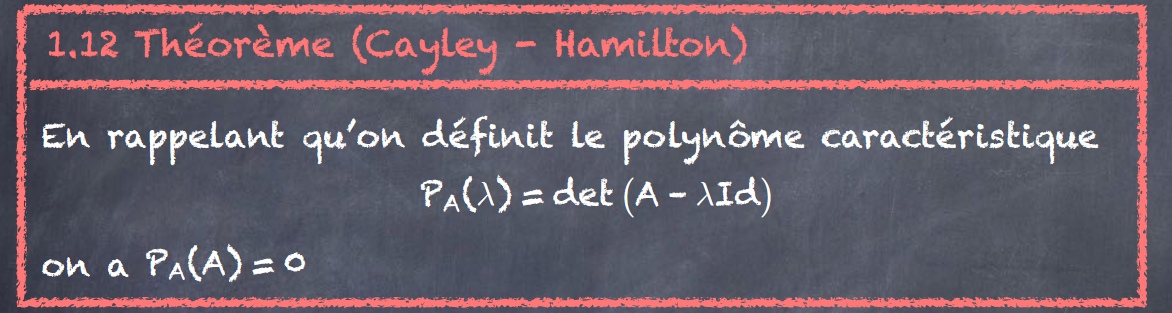
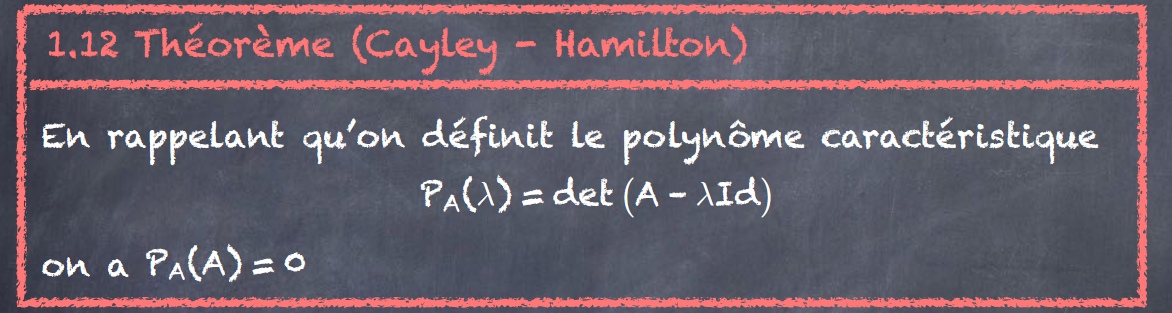
Quand dit-on qu’une suite de matrices converge ?

Quelles conditions équivalentes caractérisent la convergence des puissances d’une matrice ?