Lesson 12 : Parabola

Parabola

Is defined to be the "set of points the same distance from a point and a line

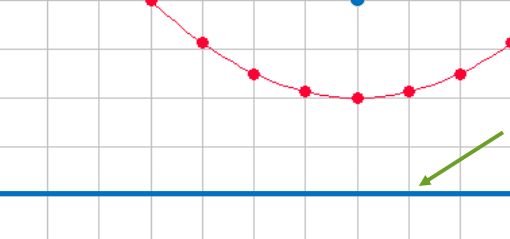
Directrix

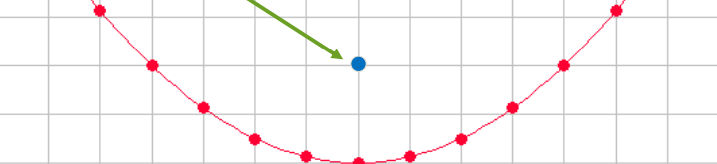
Focus

Axis of symmetry

The line perpendicular to the directrix passing through the focus

Vertex

Is the point of intersection of the axis of symmetry with the parabola

(x - h)^2 = 4p(y - k)

The equation of the parabola with vertex at (h, k), focus at (h, k + p), and directrix y = k - p

Upward Parabola

If (x - h)^2 = 4p(y - k) and p > 0

Downward Parabola

If (x - h)^2 = 4p(y - k) and p < 0

(y - k)^2 = 4p(x - h)

The equation of the parabola with vertex at (h, k), focus at (h + p, k), and directrix x = h - p

Right Parabola

If (y - k)^2 = 4p(x - h) and p > 0

Left Parabola

If (y - k)^2 = 4p(x - h) and p < 0

(x - h)^2 = 4p(y - k)
(y - k)^2 = 4p(x - h)

The two equations showing the vertex are said to be in standard form

Ax^2 + Dx + Ey + F + 0
Ax^2 + Dx + Ey + F + 0

If we perform the indicated squares and transpose the terms on the right side then we obtain the general forms

Latus Rectum

Is the line segment passing through the focus, perpendicular to the axis of symmetry with endpoints on the parabola