Integrals & Riemann Sum Function Behavior & Approximation

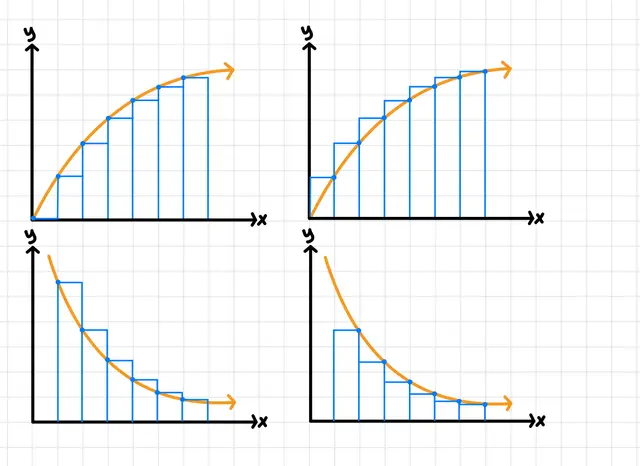
If the function behavior is increasing, a left Riemann sum would be an (underestimate/overestimate/cannot be determined).

underestimate

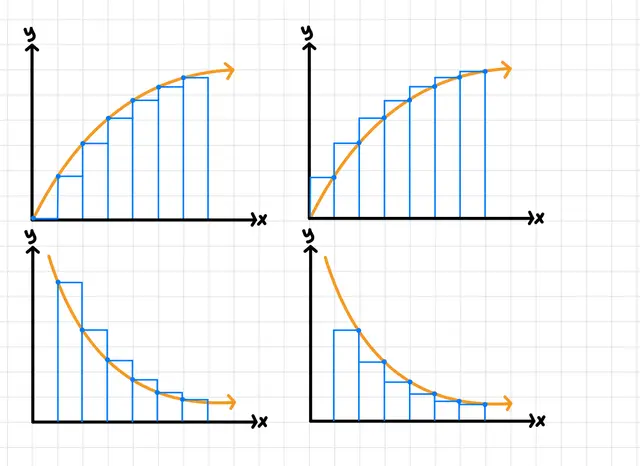
If the function behavior is decreasing, a left Riemann sum would be an (underestimate/overestimate/cannot be determined).

overestimate

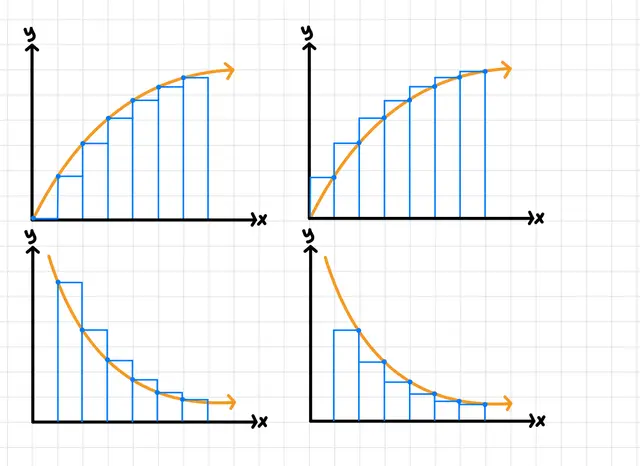
If the function behavior is increasing, a right Riemann sum would be an (underestimate/overestimate/cannot be determined).

overestimate

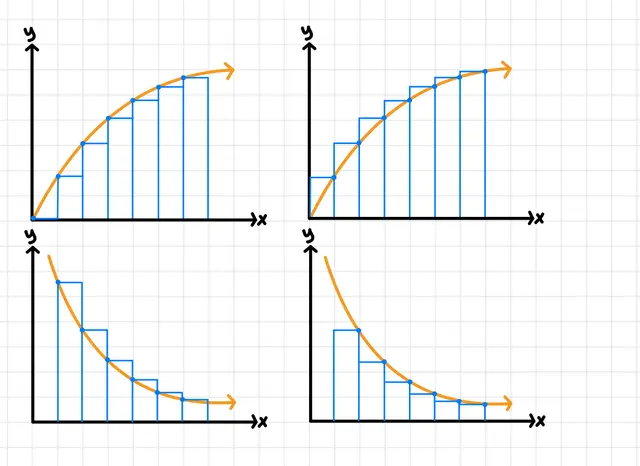
If the function behavior is decreasing, a right Riemann sum would be an (underestimate/overestimate/cannot be determined).

underestimate

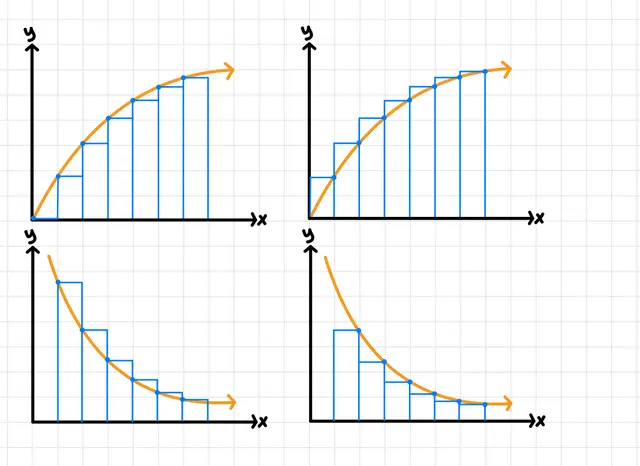
You can tell whether a left or right Riemann sum will over or underestimate because of the function’s (increasing or decreasing trends/concavity).

both

If a function goes from concave up to concave down, a left or right Riemann sum will (overestimate/underestimate/cannot be determined).

cannot be determined

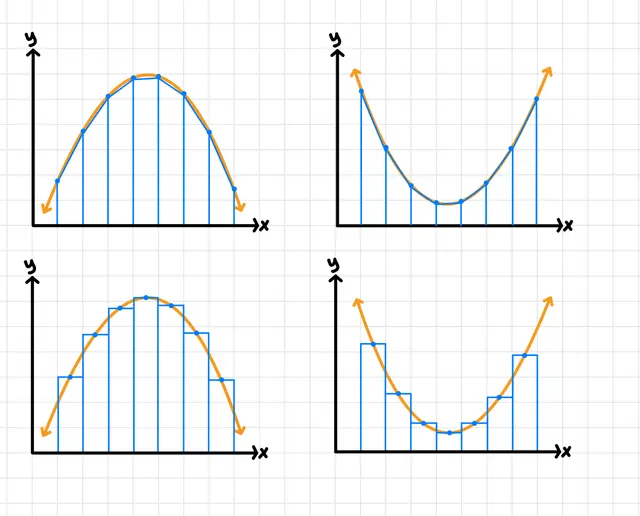
If a function is concave up, a trapezoidal Riemann sum will (overestimate/underestimate/cannot be determined).

overestimate

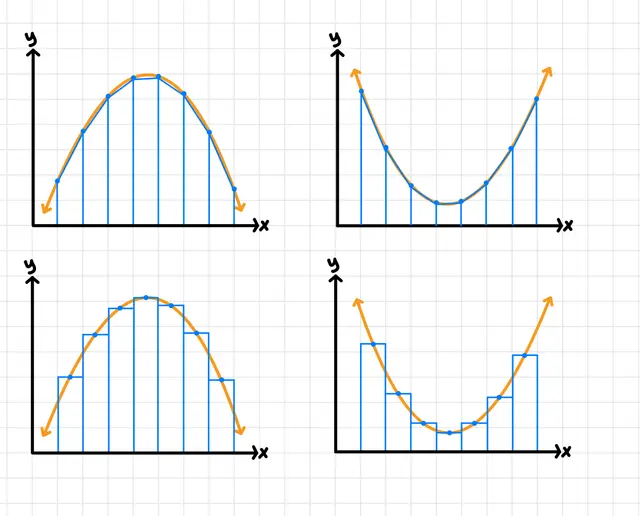
If a function is concave down, a trapezoidal Riemann sum will (overestimate/underestimate/cannot be determined).

underestimate

If a function goes from concave up to concave down, a trapezoidal Riemann sum will (overestimate/underestimate/cannot be determined).

cannot be determined

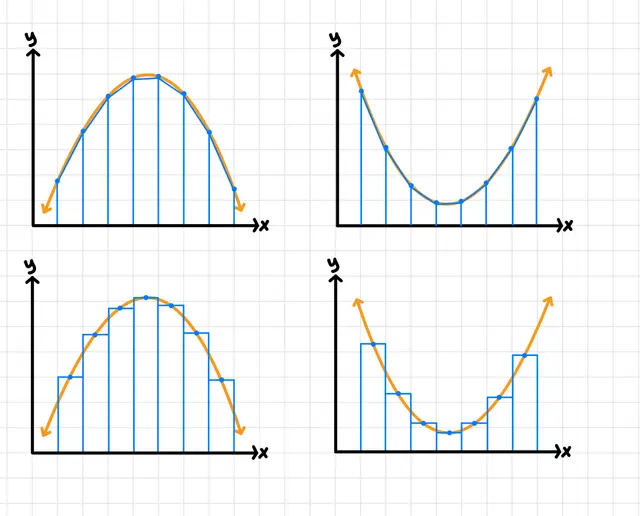
You can tell whether a midpoint Riemann sum will over or underestimate because of the function’s (increasing or decreasing trends/concavity).

concavity

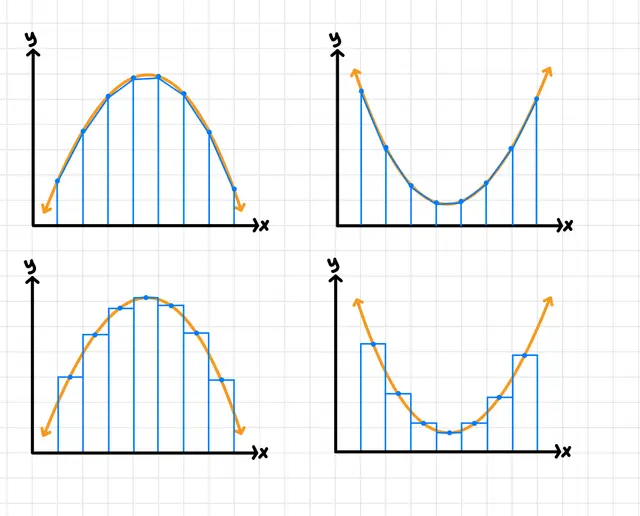
If a function is concave up, a midpoint Riemann sum will (overestimate/underestimate/cannot be determined).

underestimate

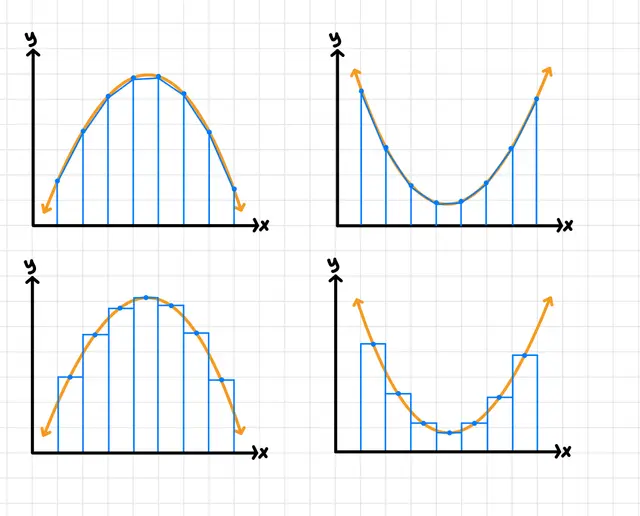
If a function is concave down, a midpoint Riemann sum will (overestimate/underestimate/cannot be determined).

overestimate

When the derivative f is positive, the antiderivative

g\left(x\right)=\int_0^{x}\!f\left(t\right)\,dt is…

increasing

When the derivative f is negative, the antiderivative

g\left(x\right)=\int_0^{x}\!f\left(t\right)\,dt is…

decreasing

When the derivative f is increasing, the antiderivative

g\left(x\right)=\int_0^{x}\!f\left(t\right)\,dt is…

concave up

When the derivative f is decreasing, the antiderivative

g\left(x\right)=\int_0^{x}\!f\left(t\right)\,dt is…

concave down

When the derivative f changes signs (crosses the x-axis), the antiderivative

g\left(x\right)=\int_0^{x}\!f\left(t\right)\,dt is…

at a local minimum/maximum

When the derivative f reaches a local extrema, the antiderivative

g\left(x\right)=\int_0^{x}\!f\left(t\right)\,dt is…

at an inflection point