Linear Algebra Final Exam Review Flashcards

Eigenvector

A vector where inputted into a linear transformation

Eigenvalue

The scalar applied to form eigen vector. Ex: T(x) = 3x. 3 is the eigen value

How to identify eigenvalues and eigenvectors geometrically

• Any inputs that form a plane - any inputs that form a line

• any inputs that form a line

Shortcut for finding determinant of 4×4 matrix

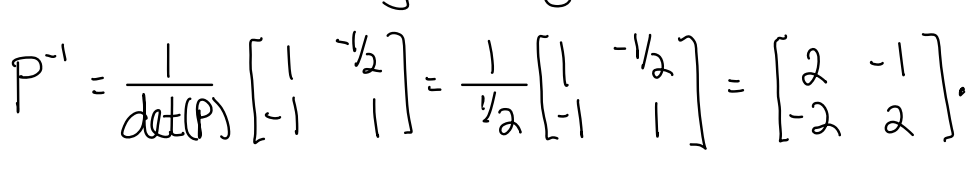
Diagonalization Theorom

If we combine the bases of two A-lambdaI matrices, we can get two LI eigenvectors. These vectors form a basis for R^n. The Matrix A is diagonalizable only if there is a basis of eigenvectors for Rⁿ

Rules for Diagonalization

g = a

if A has n distinct eigen values, then A is diagalizable

the sum of the geometric multiplicies must equal n

Scaling Eigenvectors with t

Scale it to remove any fractions to make life easier when doing diagonalization

g

dimension of a basis for a lambda value

a

algebraic multiplicities of lambda value after computing det(A-LambdaI)

If A has eigenvalue of 0

A is not invertible as det(A) = det(A-0I) = 0

Empty Set

denoted as {}

basis contains zero vectors

{0} is not LI and therefore cannot be classified as a basis (not the empty set)

However {} by itself is Linearly independent

Dimension = 0

geometric multiplicies

1<= g <= a <= n

G = dim(ker(A-lambdaI)) // REMEMBER THIS!

This is because

Elambda = ker(A-lambdaI)

G = dim(Elambda) or dim(ker(A-lambdaL))

Linear Indepence of Eigenspaces

Linearly Independent of other eigen spaces