Graph Theory
1/16
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
17 Terms
Graph Theory
a branch of discrete math that deals with the study of objects and their relations
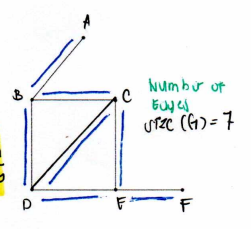
Graph
consists of vertices and edges
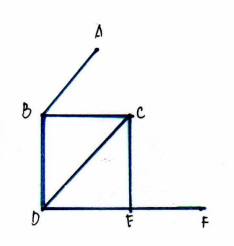
Vertices
are points in the graph
Edges
are lines “connecting” two distinct vertices
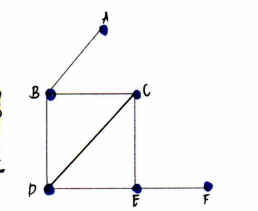
Adjacent
two distinct vertices are said to be adjacent if and only if they are “connected” by a line. Also, two distinct edges are said to be adjacent if and only if the share a common vertex
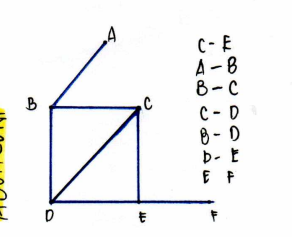
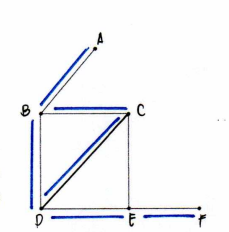
Walk
a u-v walk is a sequence of vertices beginning with u and ending at v such that consecutive vertices in the sequence are adjacent

Closed walk
a walk where the beginning and ending vertex are the same
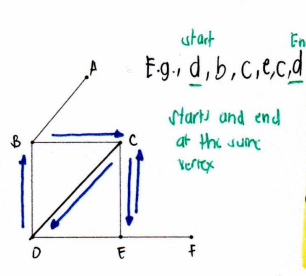
Trail
a u-v trail is a u-v walk in which no edge is traversed more than once
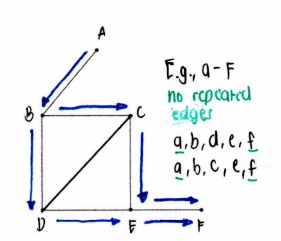
Path
a u-v path is indeed a u-v walk in which no vertices are repeated
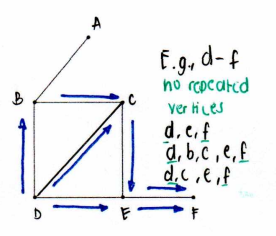
Circuit
a closed trail of length 3 or more
(like closed trail)
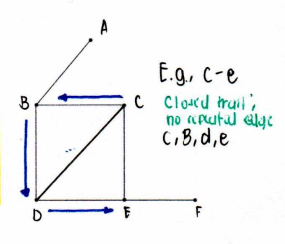
Cycle
a circuit that repeats no vertex, except for the first and last
(like closed path)

Distance
the distance between u and v is the smallest length of any u-v path
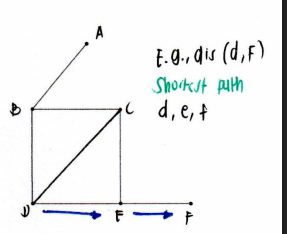
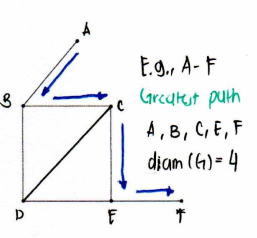
Diameter
the greatest distance between any two vertices of a connected graph
Complete graph
every two distinct vertices of the graph is adjacent with each other
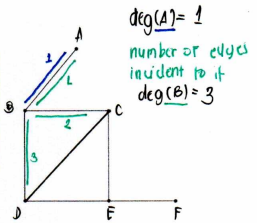
Degree
the number of edges “connected” with v is called the degree of v
Order
the number of vertices on a graph
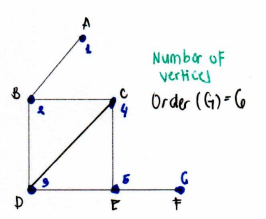
Size
the number of edges on a graph