Electrostatics
1/87
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
88 Terms
For the simple problem of two isolated point charges, Coulomb’s Law is defined as:
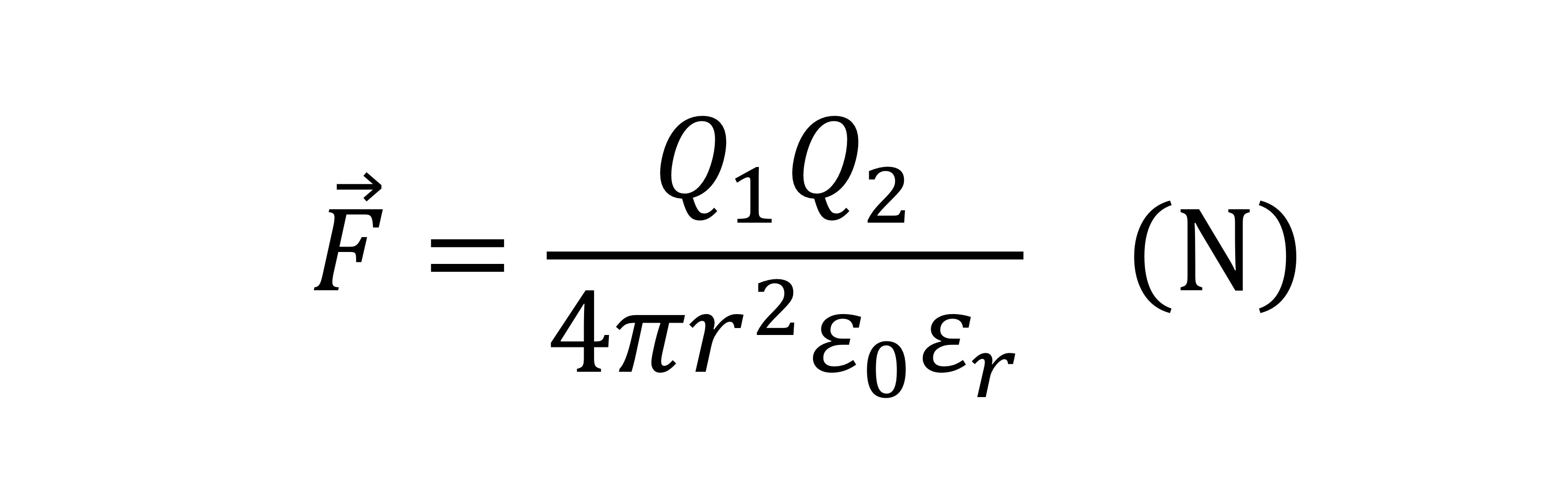
Like charges
Repel each other
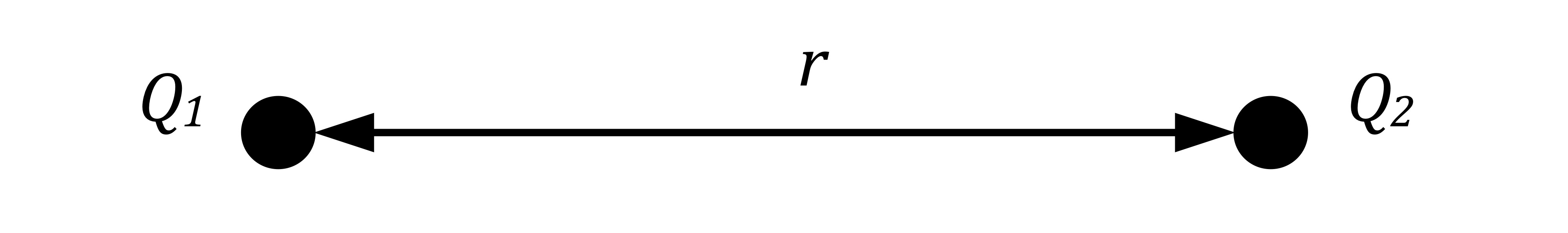
The electric force acts
Along a line between two charges
The magnitude of electric force is inversely proportional to
The square of the distance between the charges
If Q1 and Q2 have the same polarity, the force
The force is repulsive and positive
If Q1 and A have the opposite polarity, the force
The force is attractive and negative
1A is
1 amp = 1 coulomb flowing for 1 second
1C is the charge of
6.24×10^18 electrons
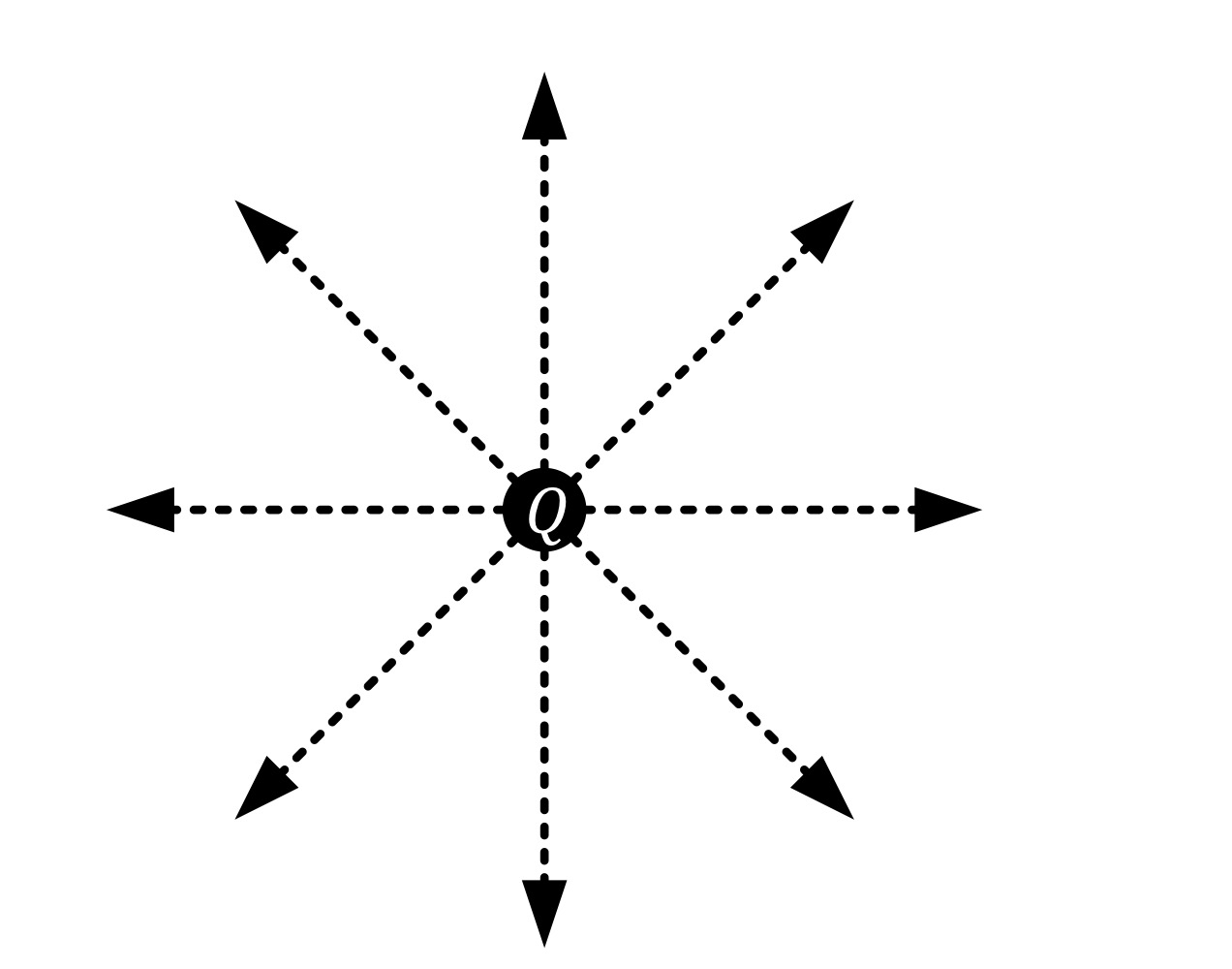
The force distribution
Acts equally in all directions and is distributed over a spherical surface surrounding the point charge
Area of sphere
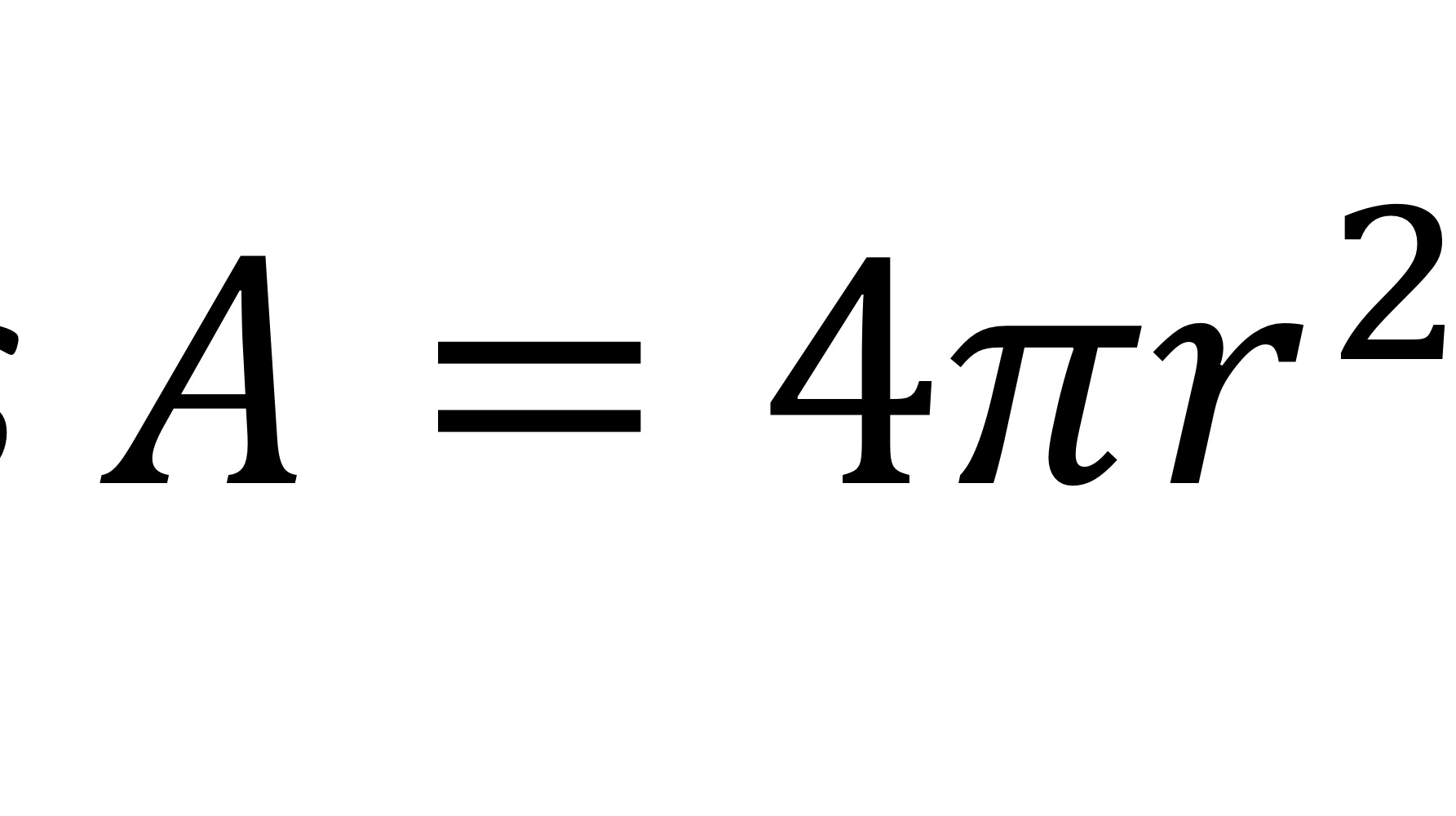
Volume of sphere
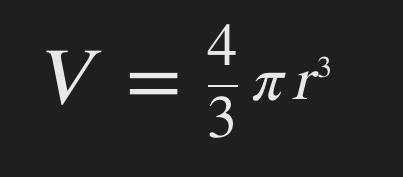
𝜀0 is
the permittivity of free space (vacuum) ( 8.854 × 10^−12 C^2/Nm^2)
𝜀𝑟 is
the relative permittivity of the surrounding material (dimensionless) (𝜀𝑟 = 1 for free space)
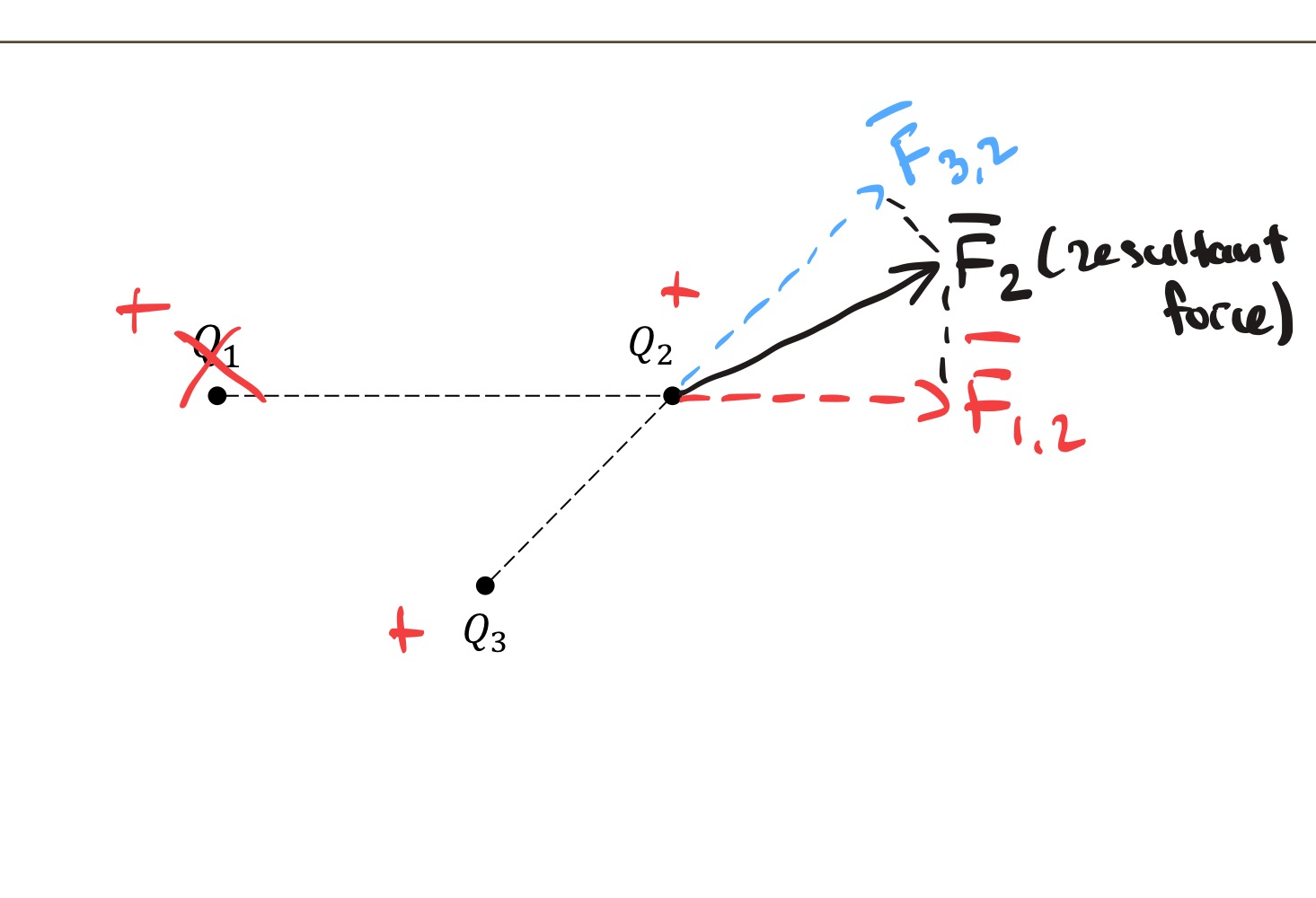
Where multiple charges are present, the force experienced by any given charge is
the vector sum of the forces on that charge resulting from each of the other charges. This is the principle of superposition. Because the forces are vector quantities, the magnitudes alone cannot be summed unless all the forces act along the same line.
Superposition of electric forces simple example
Electric Field
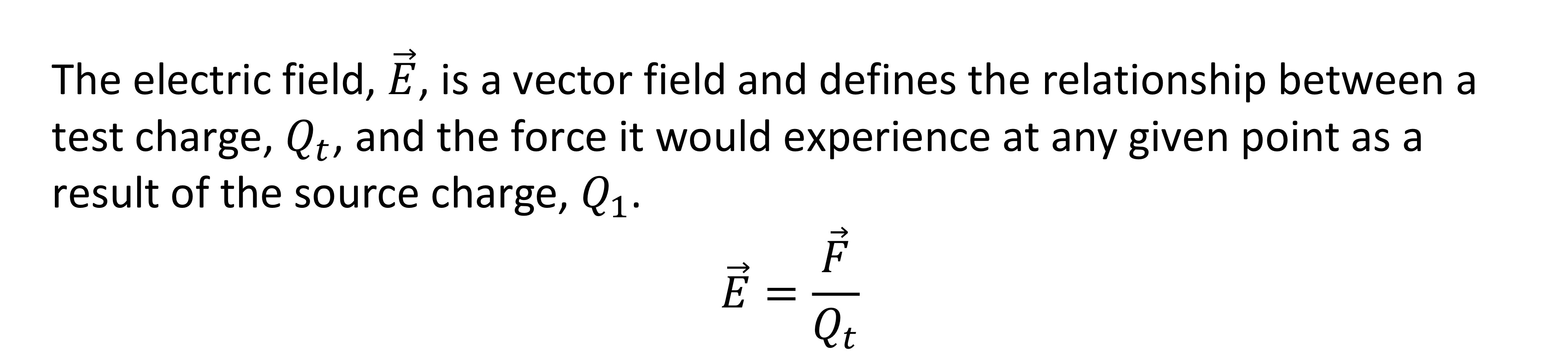
electric field, 𝐸, resulting from charge 𝑄1 is given by:
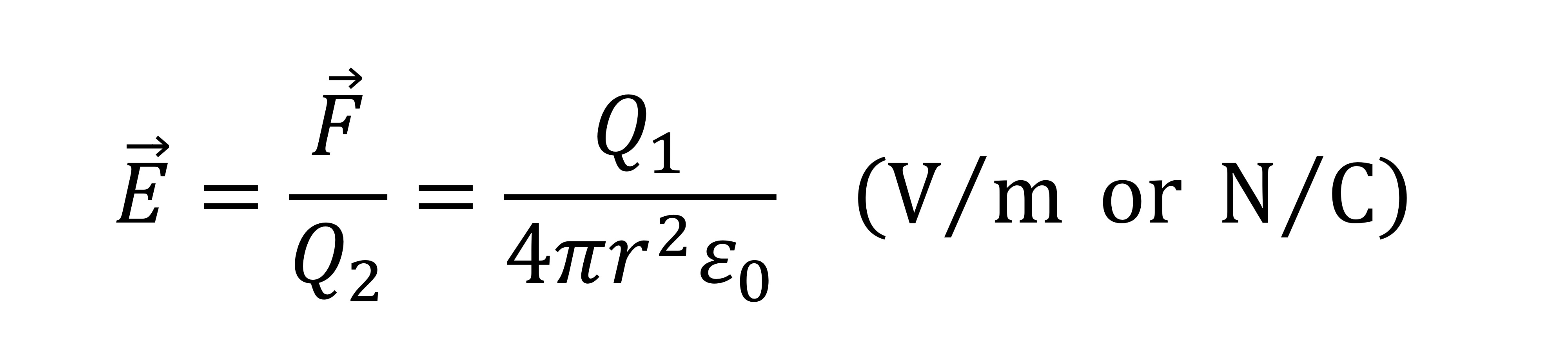
Electric Field’s direction
Their direction is in the direction of
the force that would be experienced by a
positive point charge.
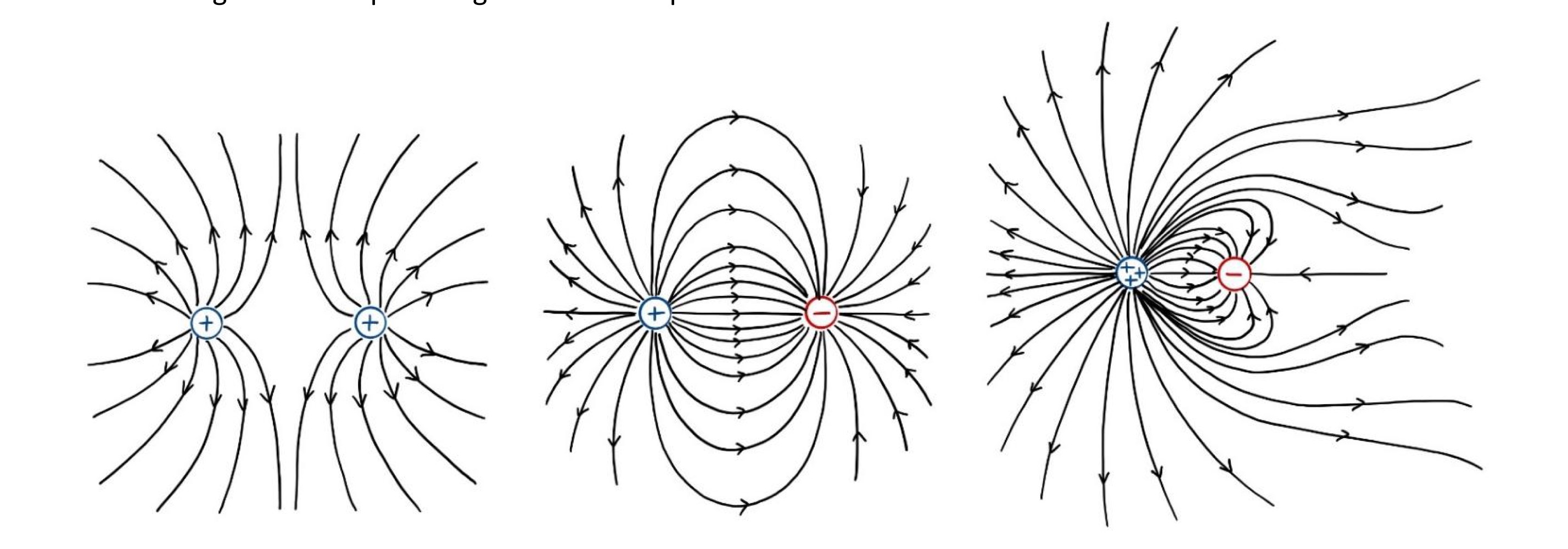
Examples of complex electric fields
On pic 3 field will eventually be uniform field of charge +2
Units of electric field
N/C or V/m
Potential energy of charge how is gained
If electric field does this work by itself (e.g. opposite charges attract) then the charge gains kinetic energy and loses potential.
If charge is moved by external agent then potential energy increases.
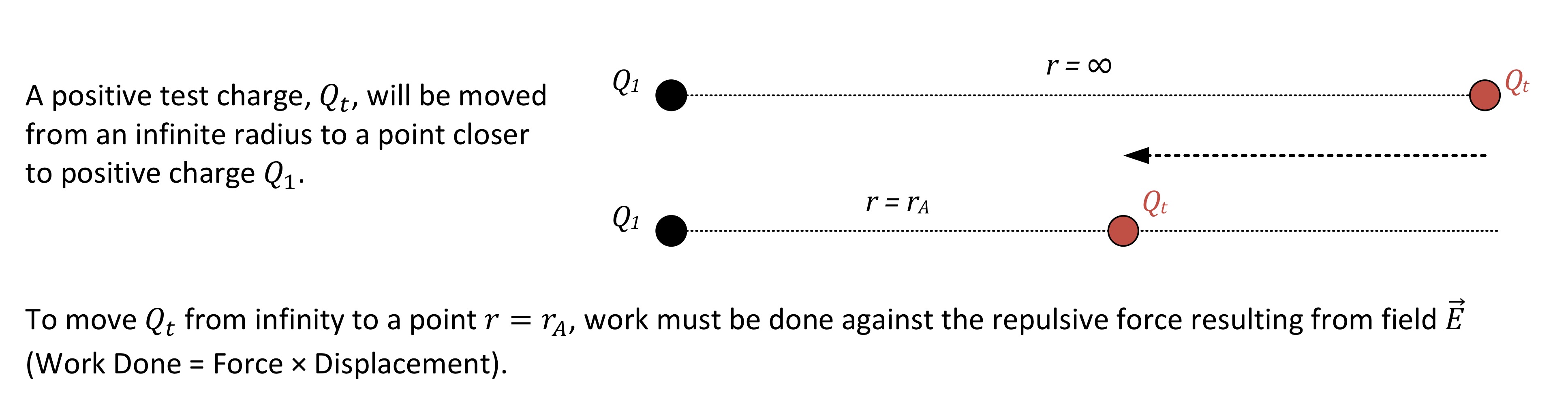
Relationship between the potential energy and work done by the field

Formula of potential energy in electrostatic
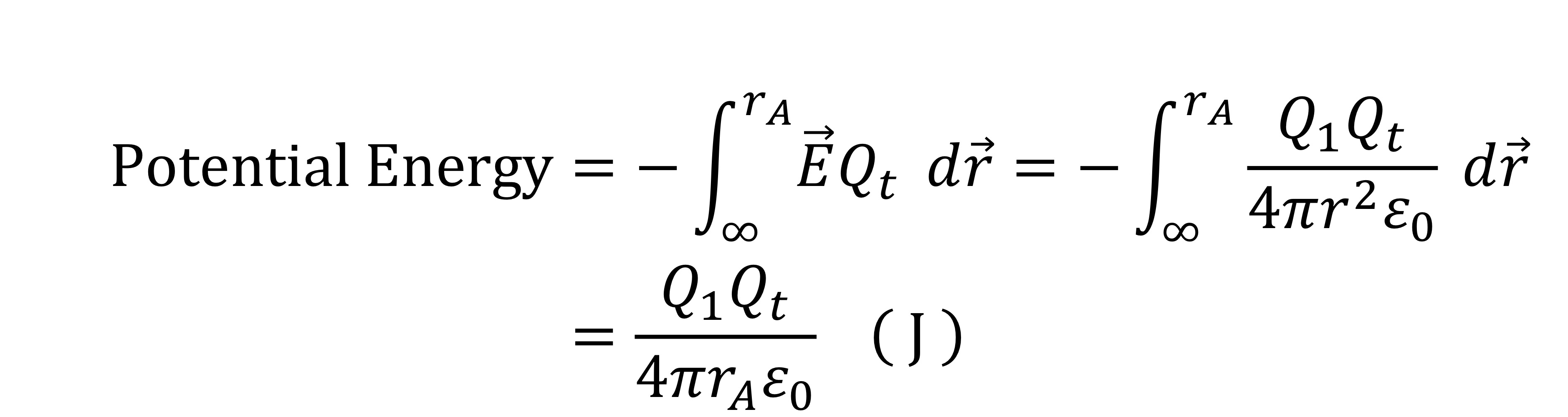
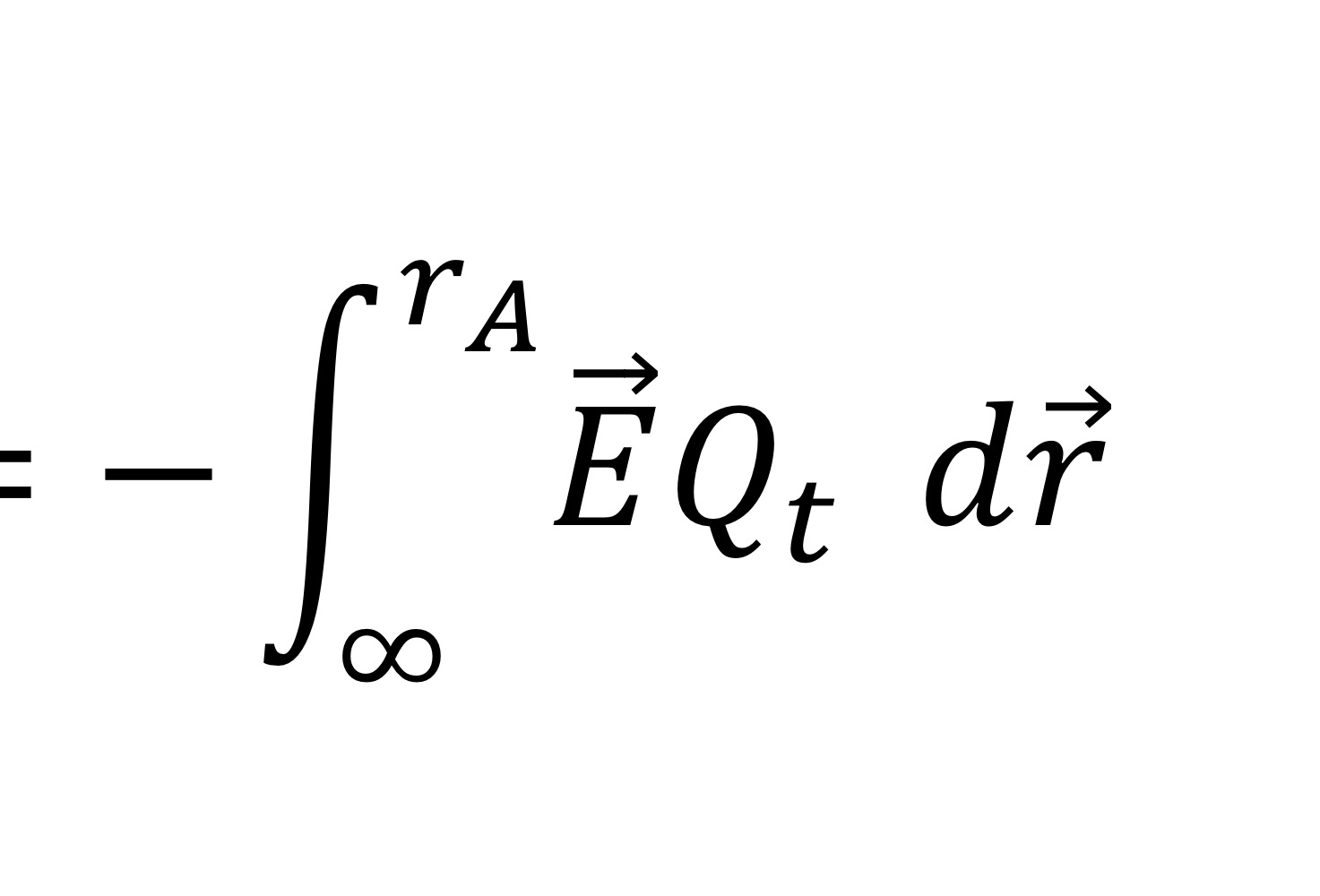
Why is potential energy a negative integration
Minus appears due to the putting rA and infinity to opposite places. The greater value usually should be on the top.
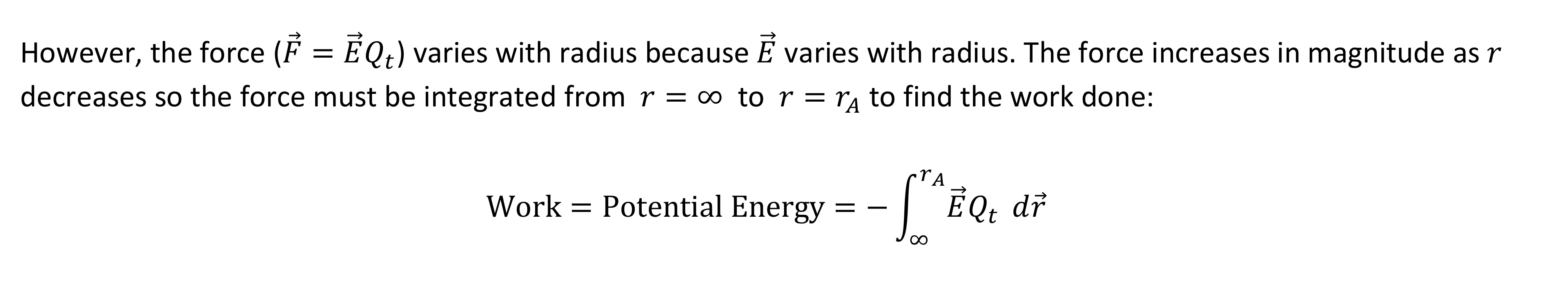
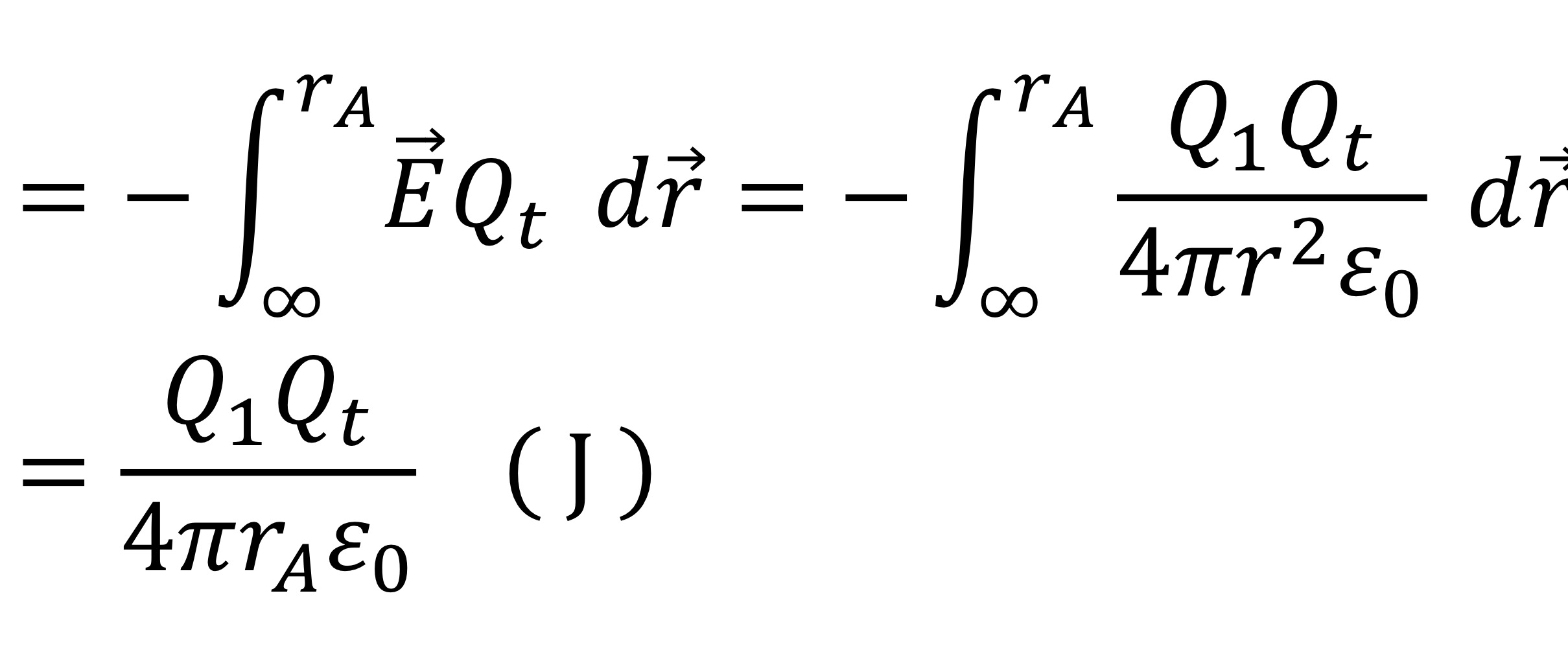
Maths behind
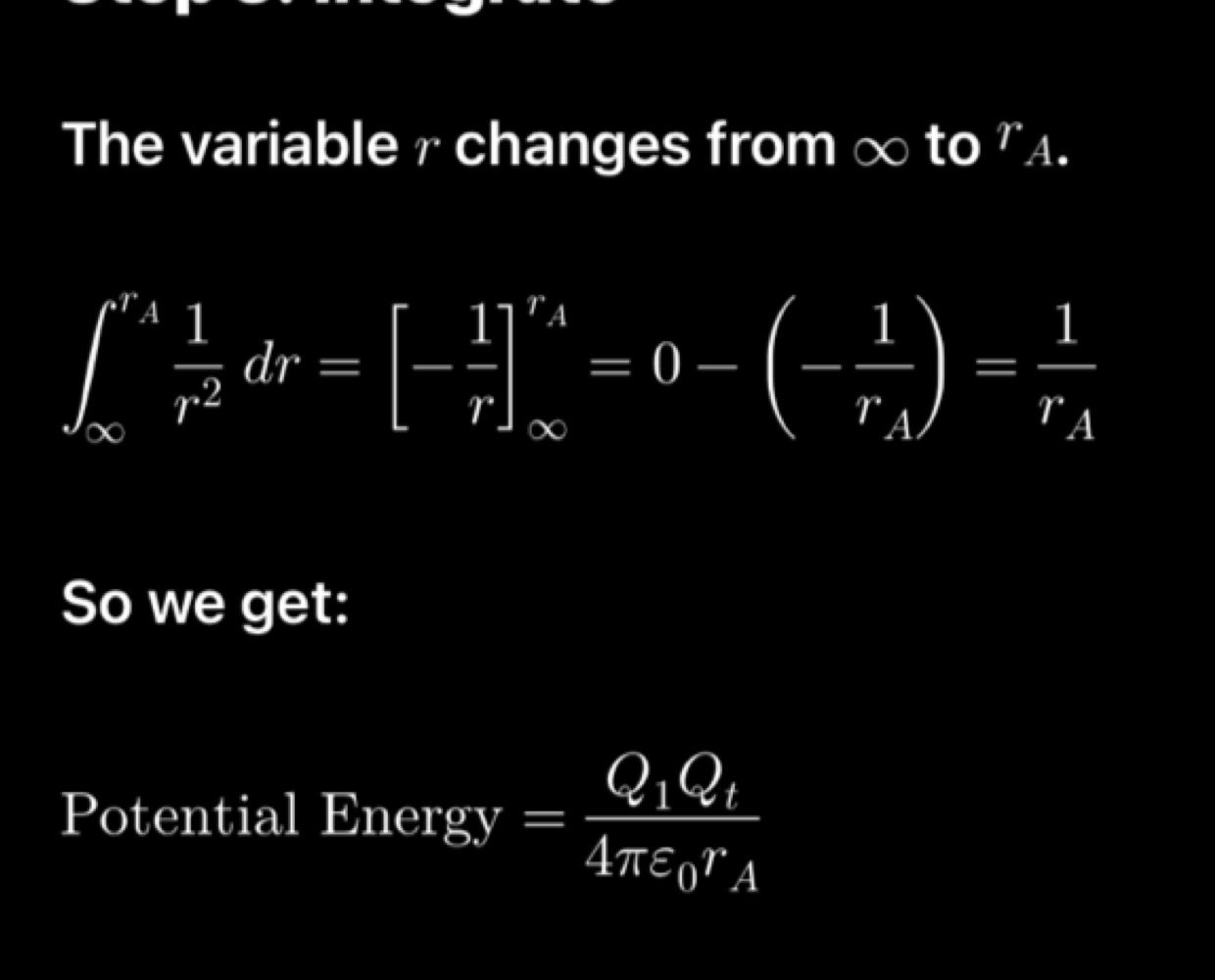
What is electric potential

Formula of electric potential
Units are volts (V)
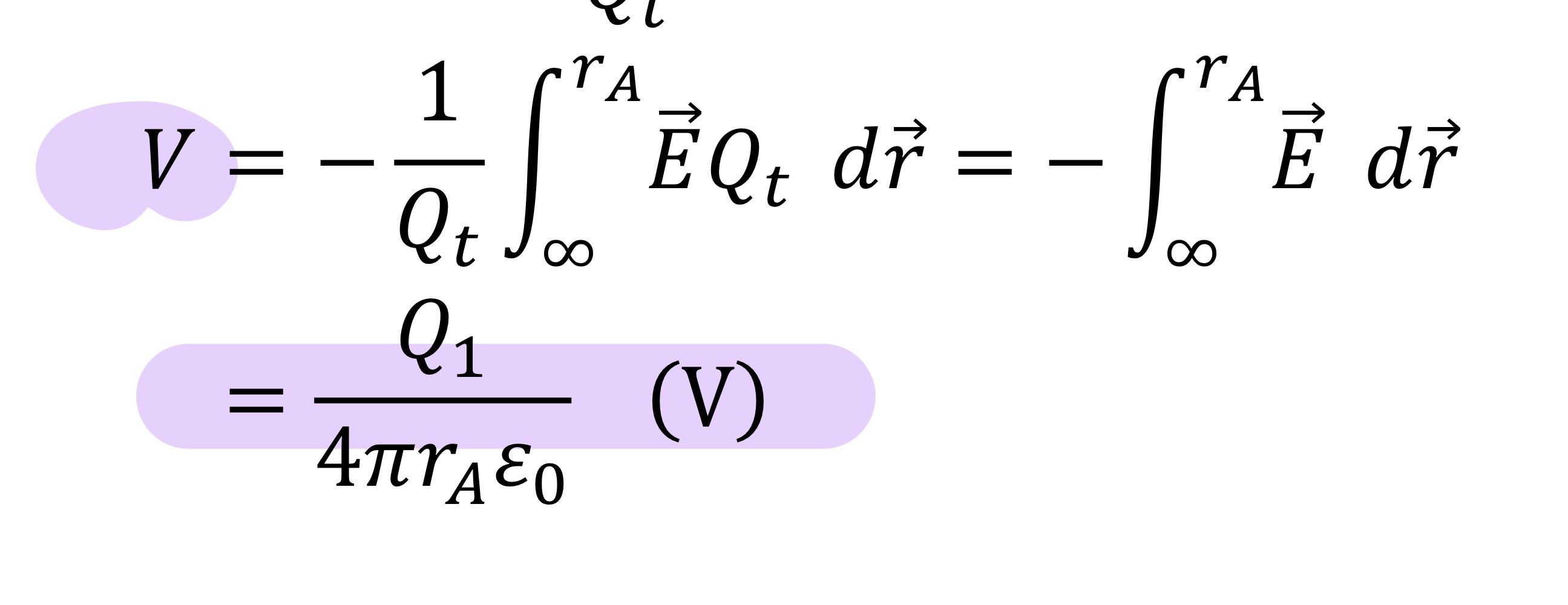
Electric potential is vector or scalar quantity
V is scalar so the principle of superposition can be applied
Potential difference

Equipotential surface
This is a surface over which the electric potential is constant. Moving a charge over an equipotential surface requires no work. Similarly, moving a charge in any closed path requires no work as its start and finish potentials are the same (the charge has returned to its original point). 90 degrees from field line
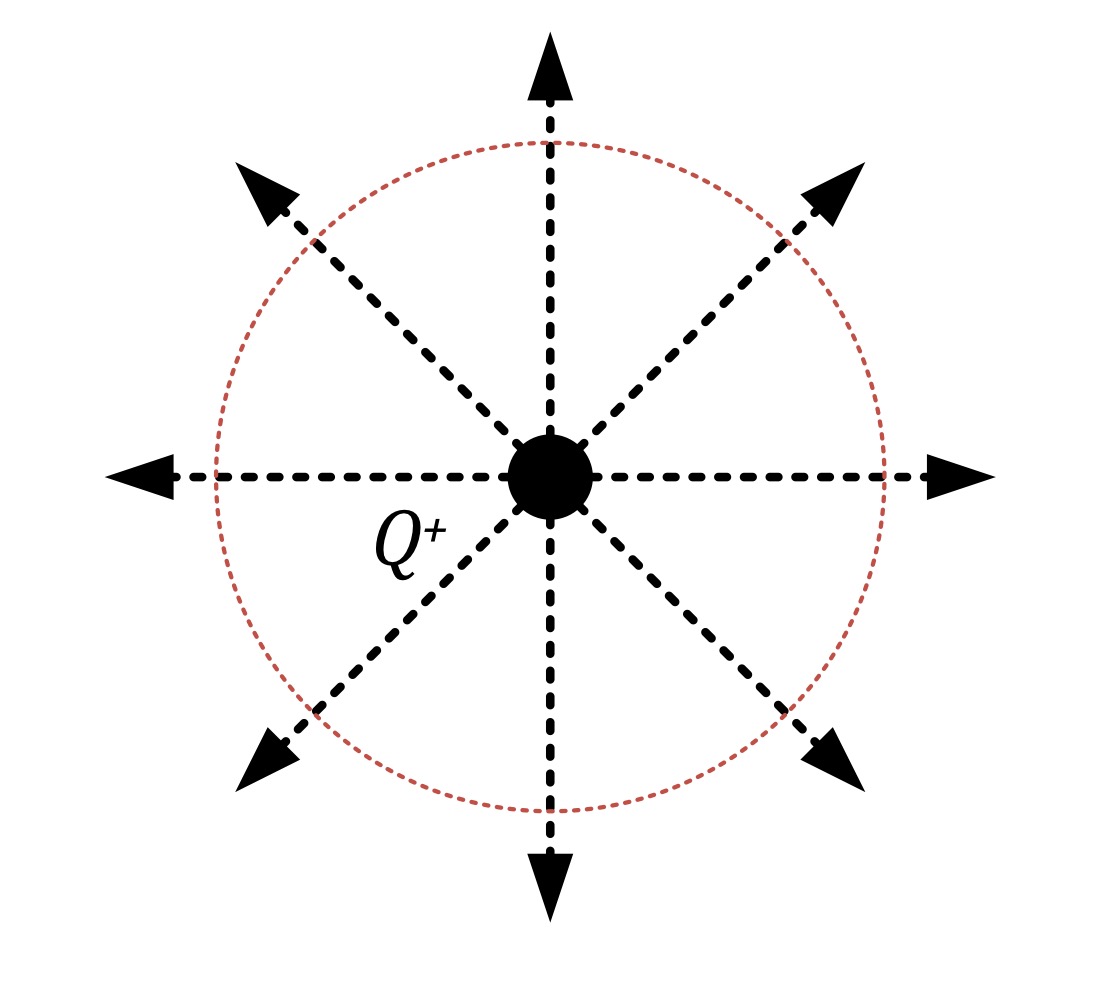
Complex examples of equipotential surfaces
Electric flux, ФD
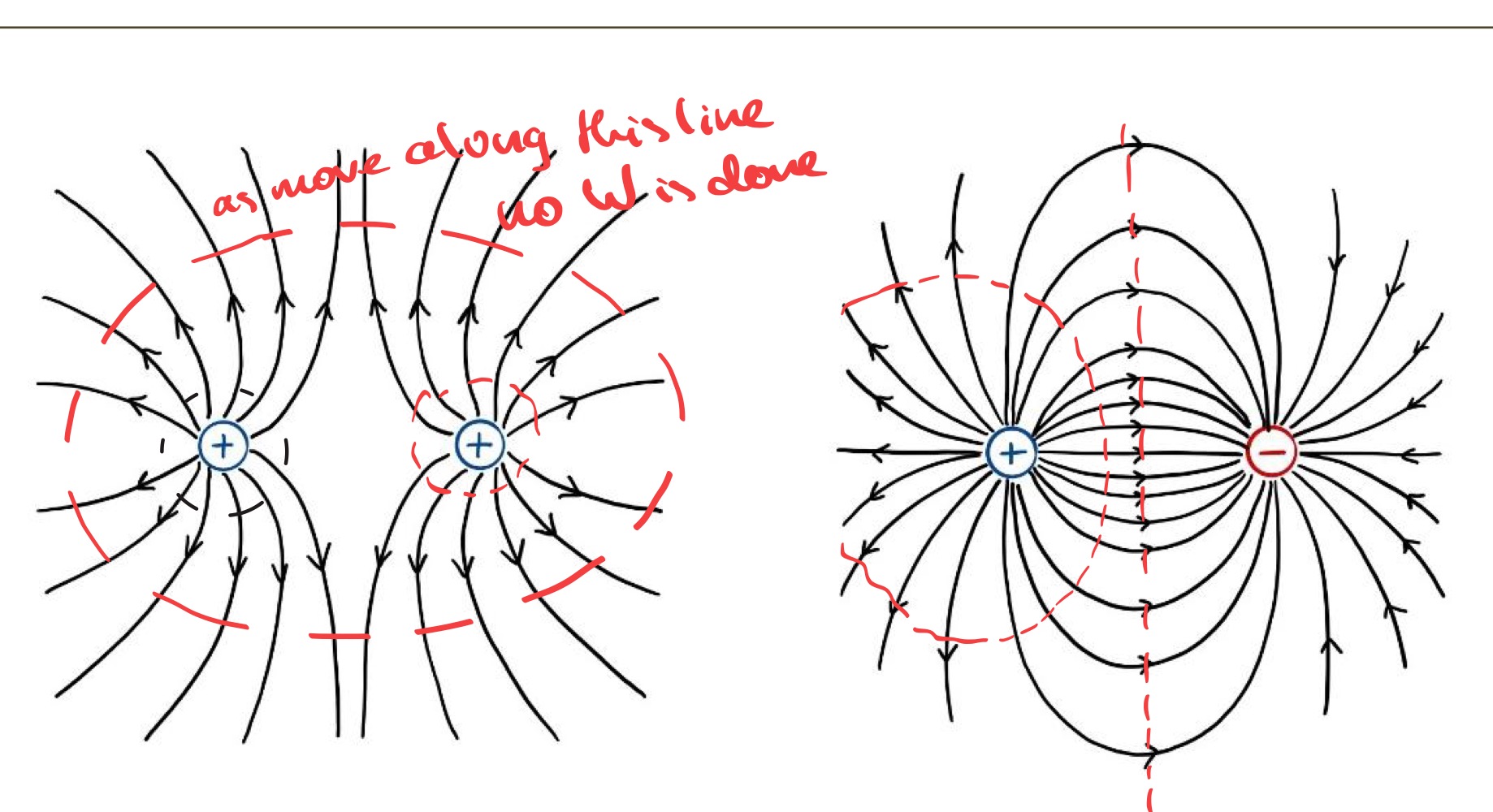
Electric flux, Φ𝐷, (Units: C) is a measure of electric field and provides a representation of how a field is distributed in space. ‘Lines of electric flux’ follow the electric field from positive to negative charges (or infinity if no other charges are present). They are primarily a means of visualising an electric field.
Electric Flux Density, D, is
Electric flux density, 𝐷 , describes the electric flux in any particular region of a system. More tightly packed ‘lines of flux’ represent a higher flux density.
Relationship between electric flux density D and electric field E

Flux density relates to… independent of…
Flux density is independent of material properties; it relates to charge and geometry.
For a given material, higher flux density represents
A stronger electric field
Formula of electric flux

Formula of electric flux density
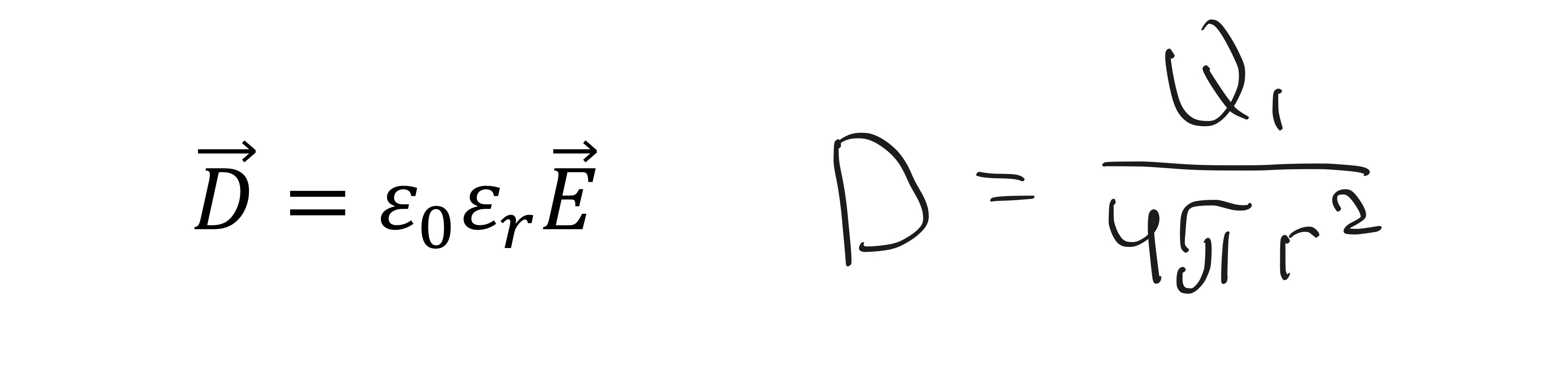
Electric field depends on
Material properties
Gauss’s Law is

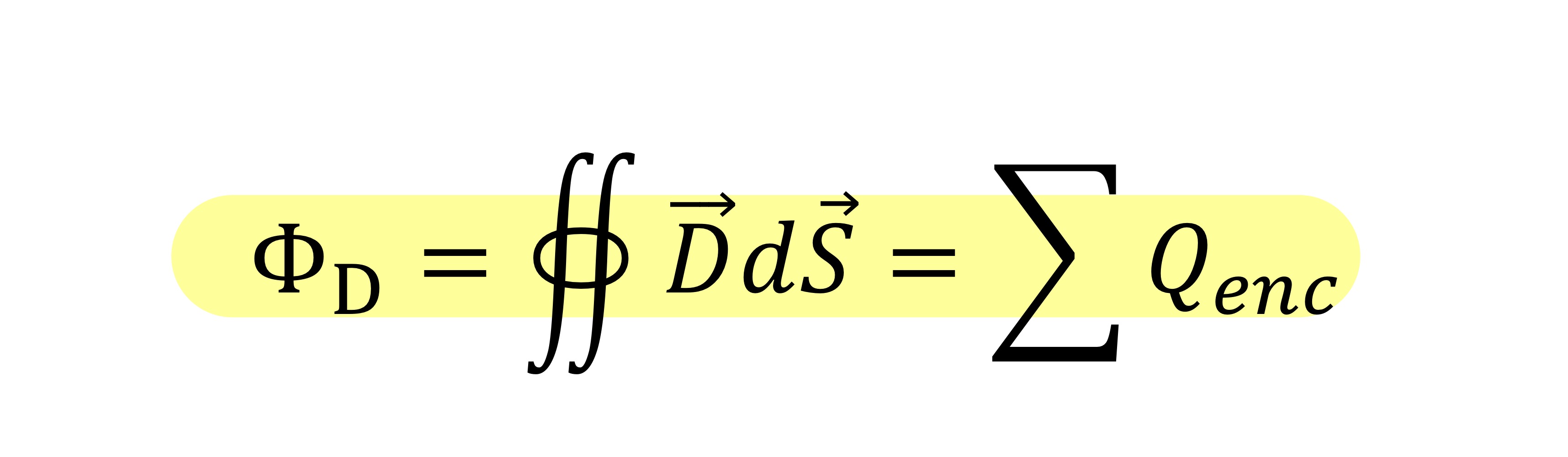
Why is it double integration
We find area of 3D shape (graph with 3 axis: x, y, z)
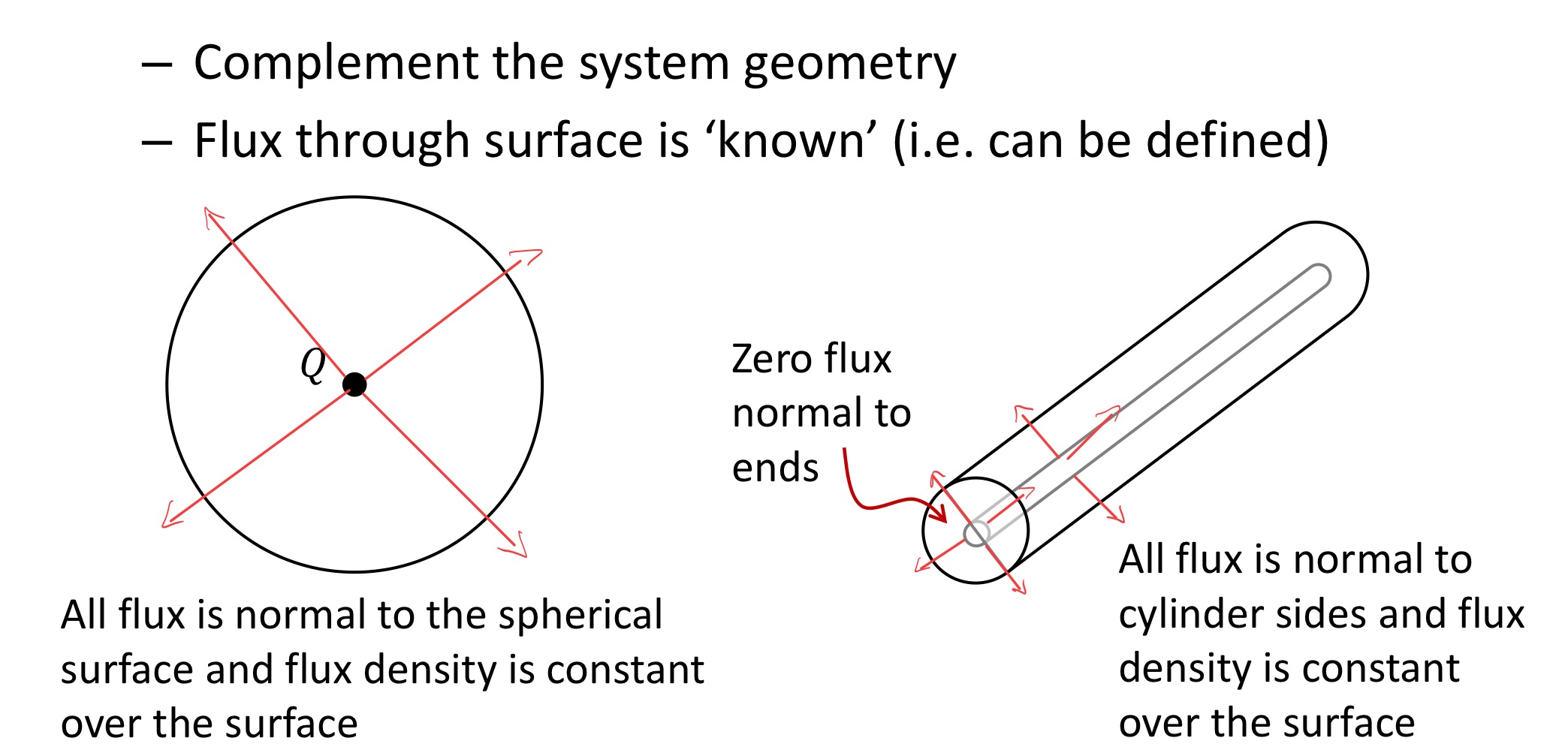
How do we apply Gauss’s Law
To apply Gauss’ Law, we select a Gaussian surface. A Gaussian surface is a closed surface that is generally selected to complement the geometry of the system under analysis (although it could be any closed surface) such that the flux through each face of the surface is ‘known’ (i.e. the flux through the surface can be easily defined). A spherical Gaussian surface would be most appropriate for a point charge as all flux will be normal to the spherical surface and evenly distributed over the surface. Similarly, a cylindrical Gaussian surface would be most appropriate for a long, straight conductor as flux will be radial to the conductor and therefore normal to the cylindrical surface.
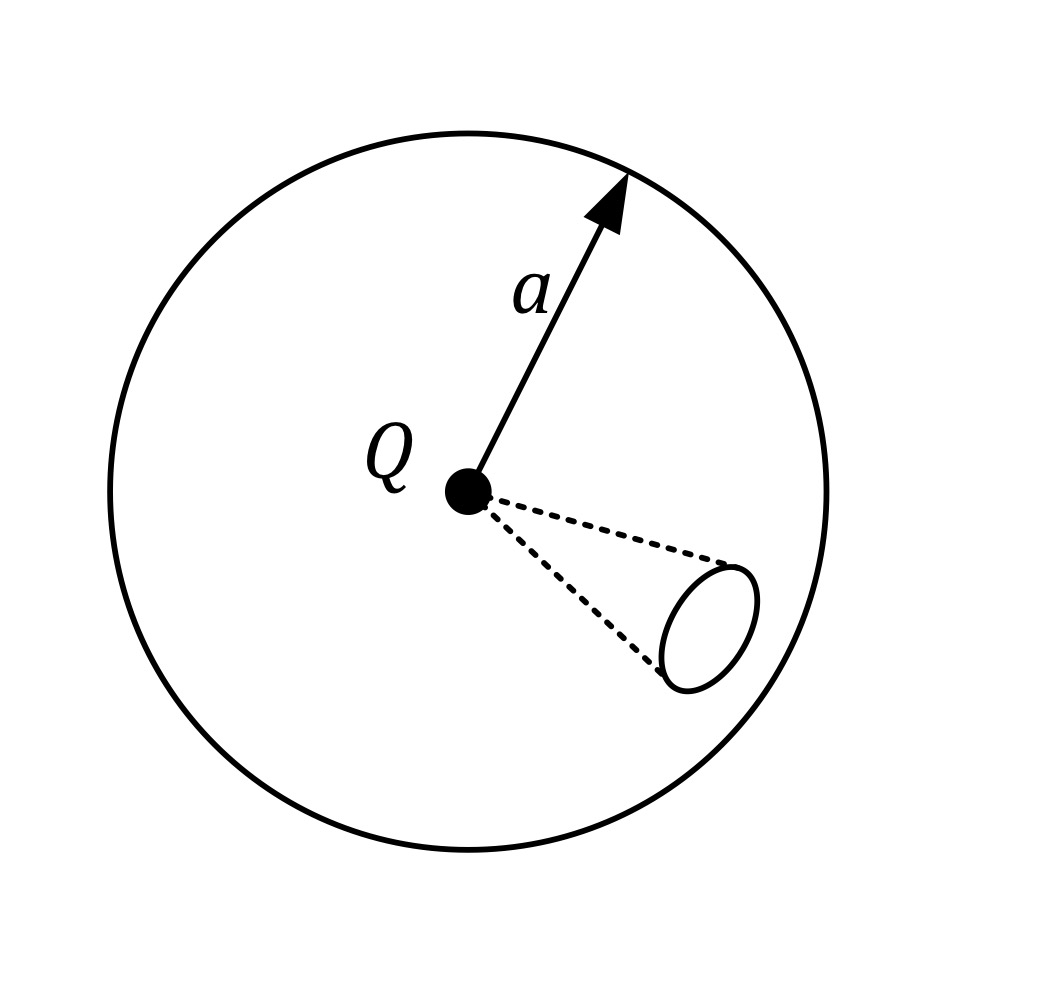
Apply Gauss’s Law
Then rearrange equation for D: D=Q/4pia²
Given that 𝐷 = 𝜀0𝜀𝑟𝐸:
E = 𝑄/4𝜋𝜀0𝑎²
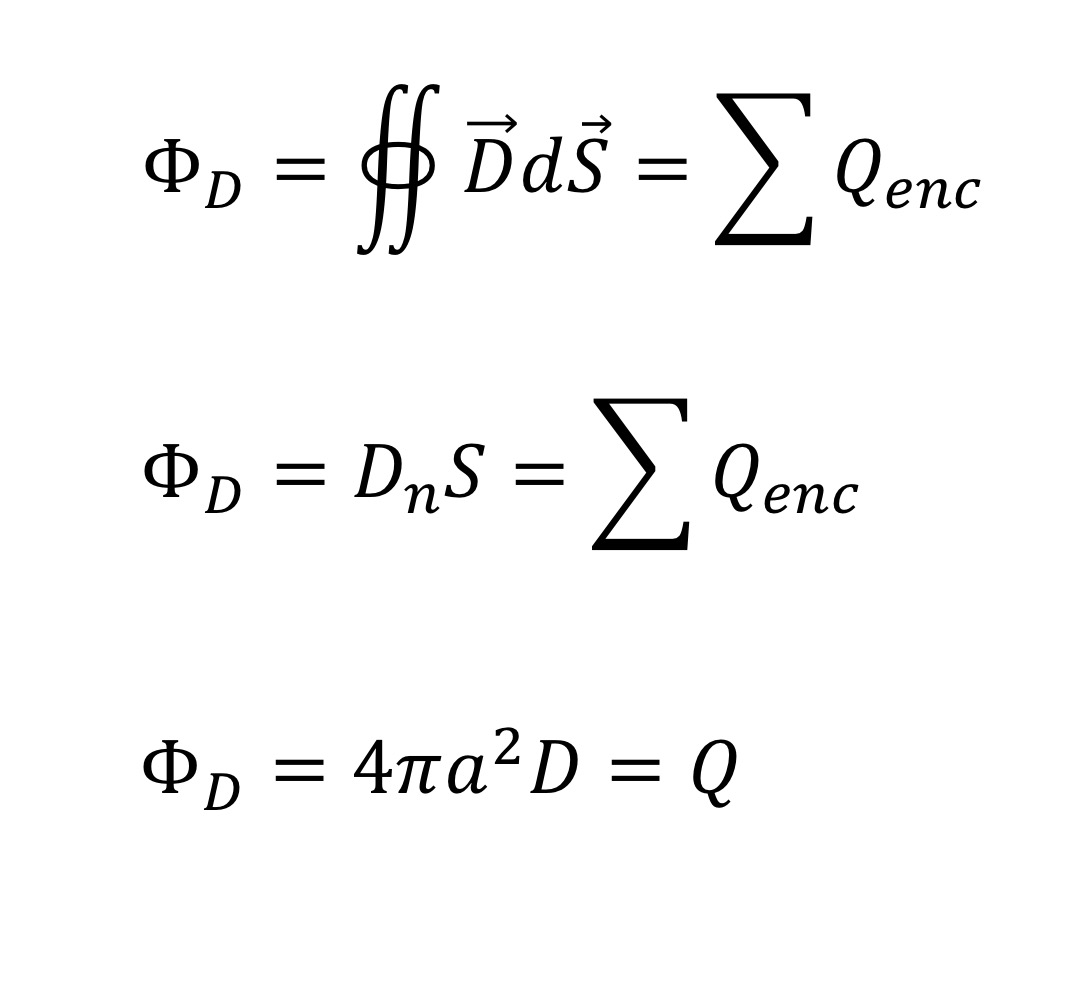
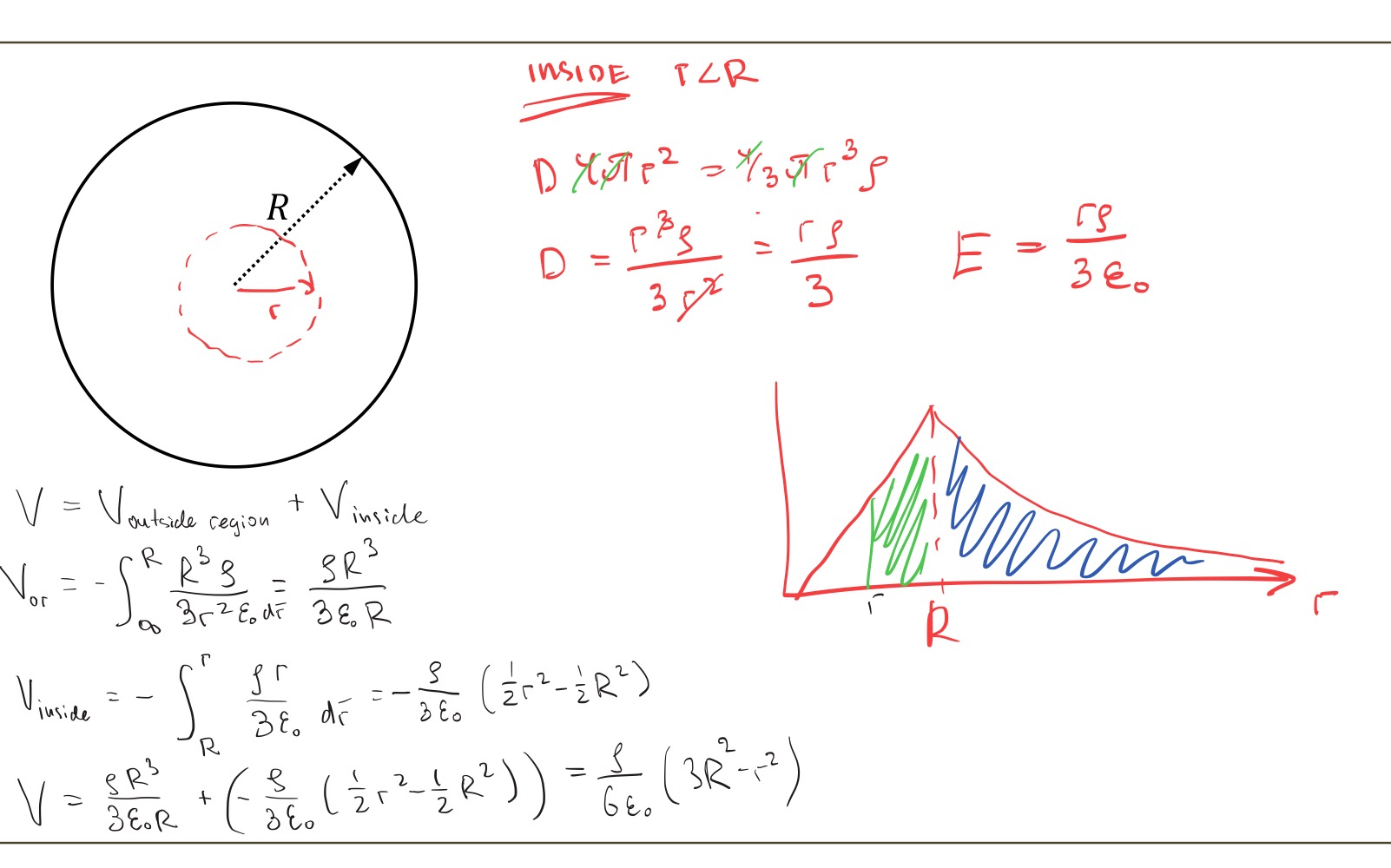
What is the electric field strength inside a conducting
sphere?
Where is the charge located?

Area under electric field distance graph is
Potential
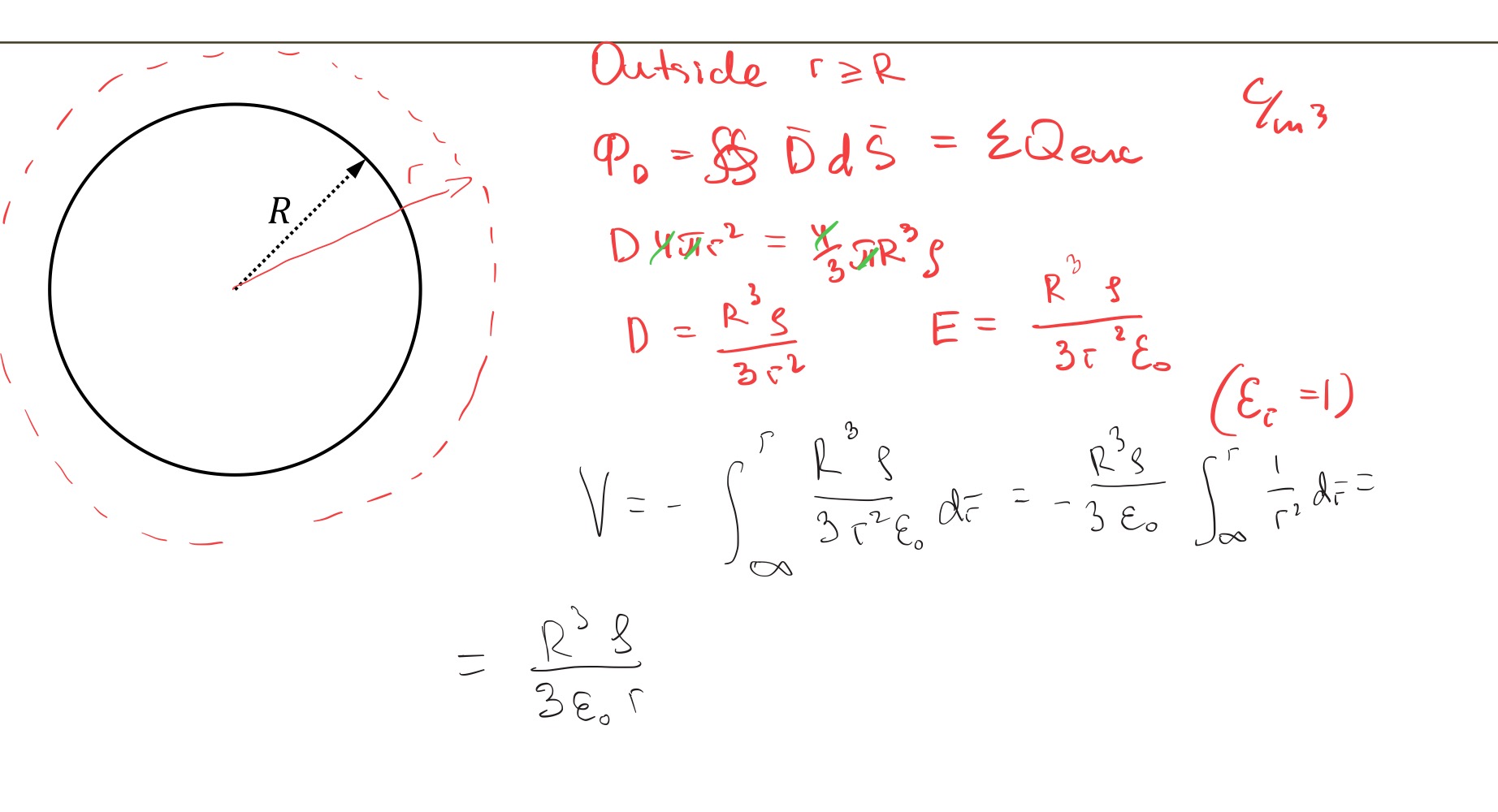
How to find potential outside the conducting sphere
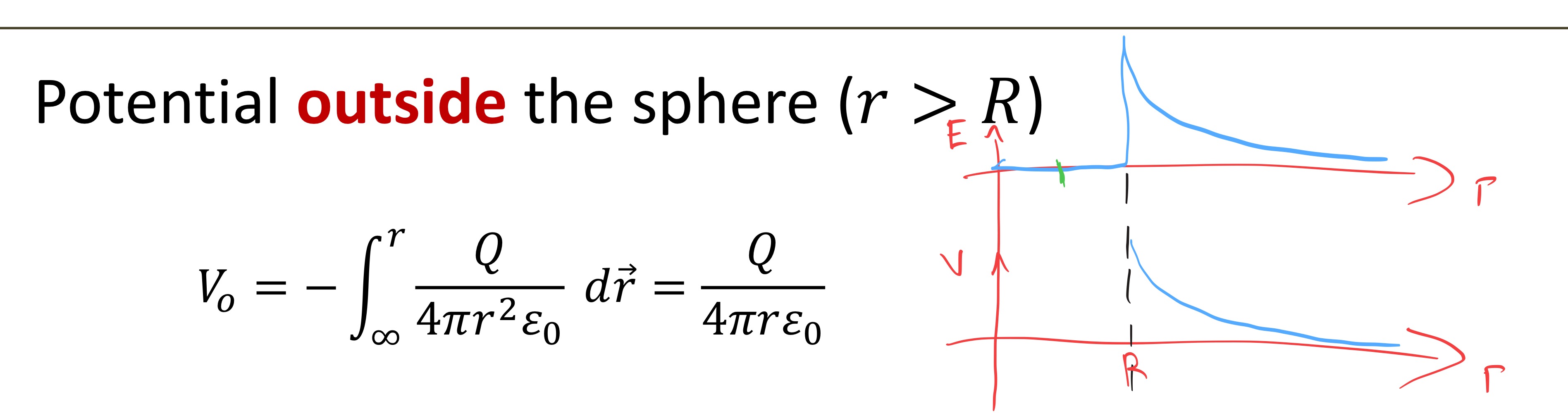
How to find potential inside the conducting sphere

How to find potential outside the non-conducting sphere
As charge is not free to move around
How to find potential inside the conducting sphere
Capacitance
a measure of a system’s ability to store energy in an electric field and is defined as the charge stored per volt (potential difference). Capacitance is given in ‘farads’ (F).
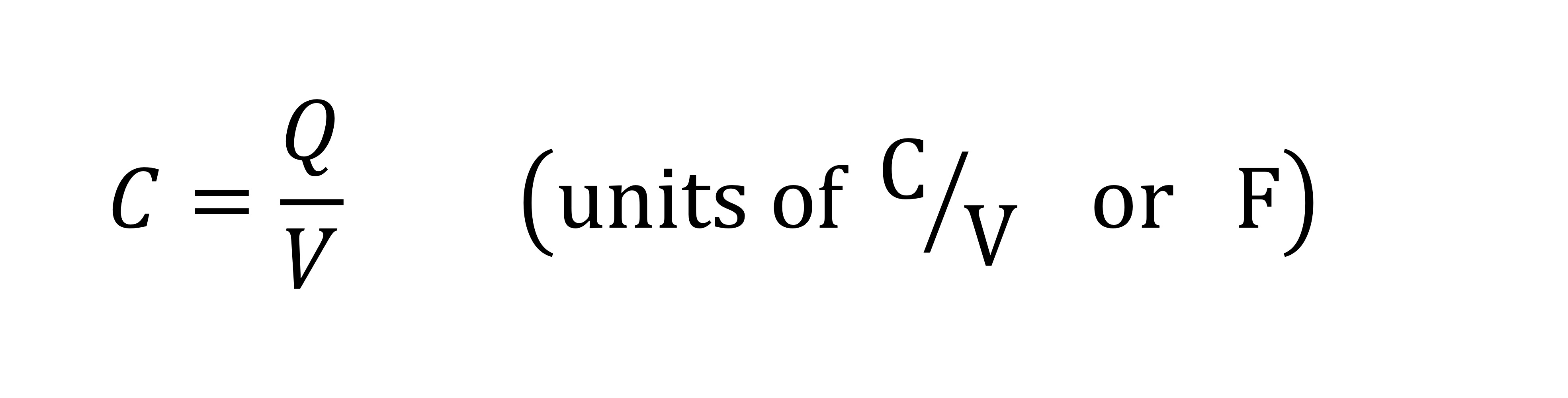
Capacitance depends on
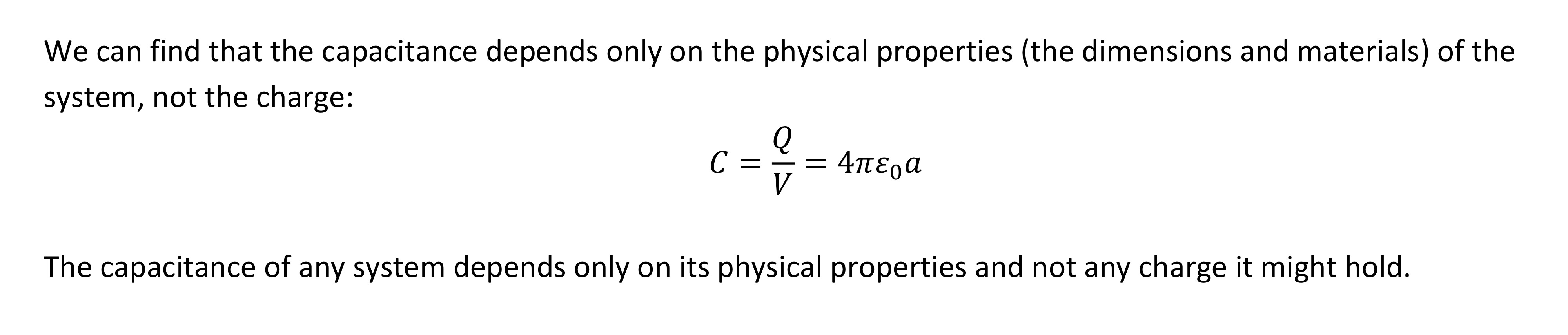
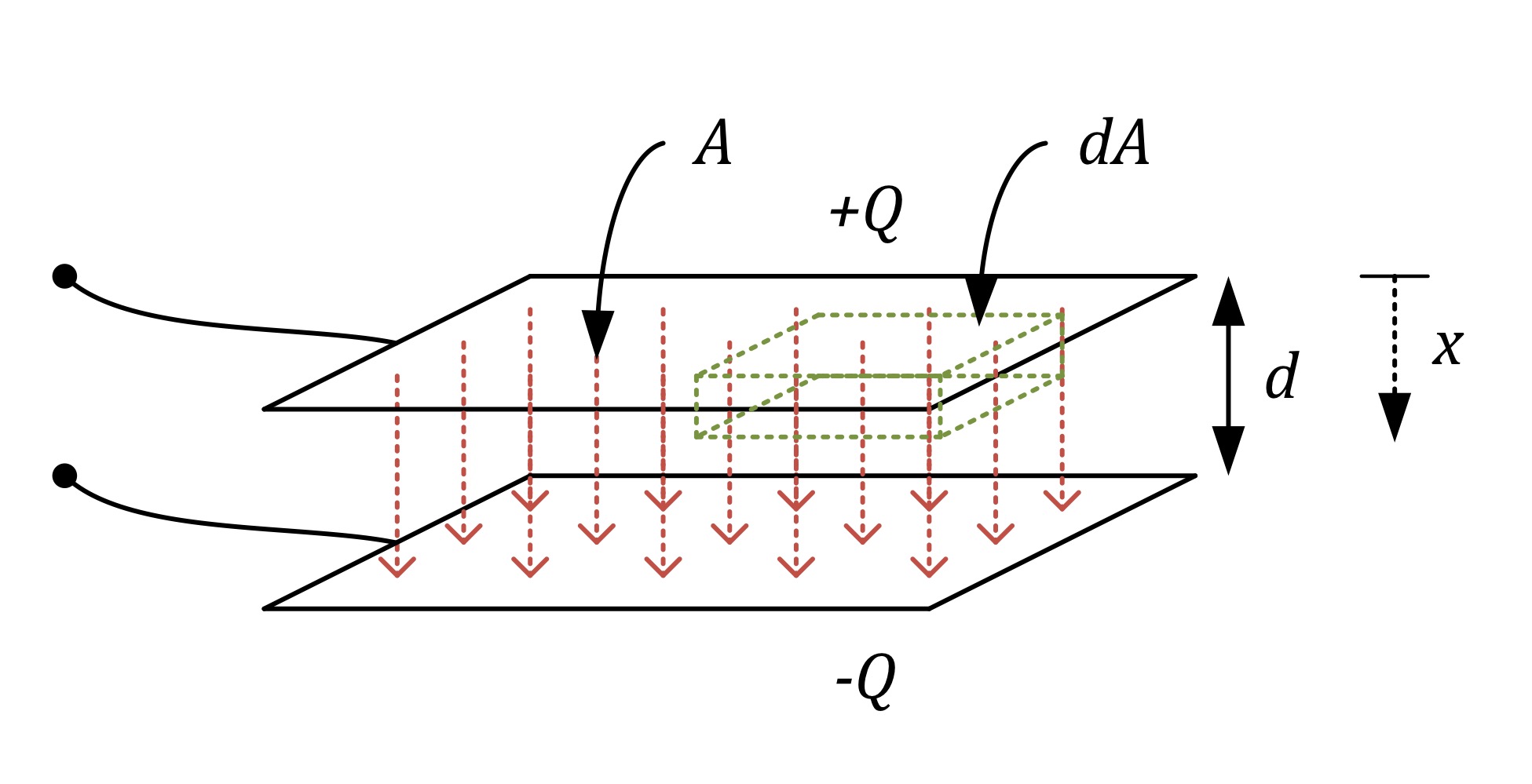
Assume we have two parallel conducting plates separated by air (free space). The plates are separated by a distance 𝑑 and have a cross-sectional area 𝐴. Each plate holds charge of magnitude 𝑄 but opposite polarity. Neglecting fringing at the edges of the plates, find the capacitance of the system.

The work done (and therefore the energy stored) during the charging process for a capacitor can be found by
integrating the voltage across the capacitor with respect to the charge held on the plates.
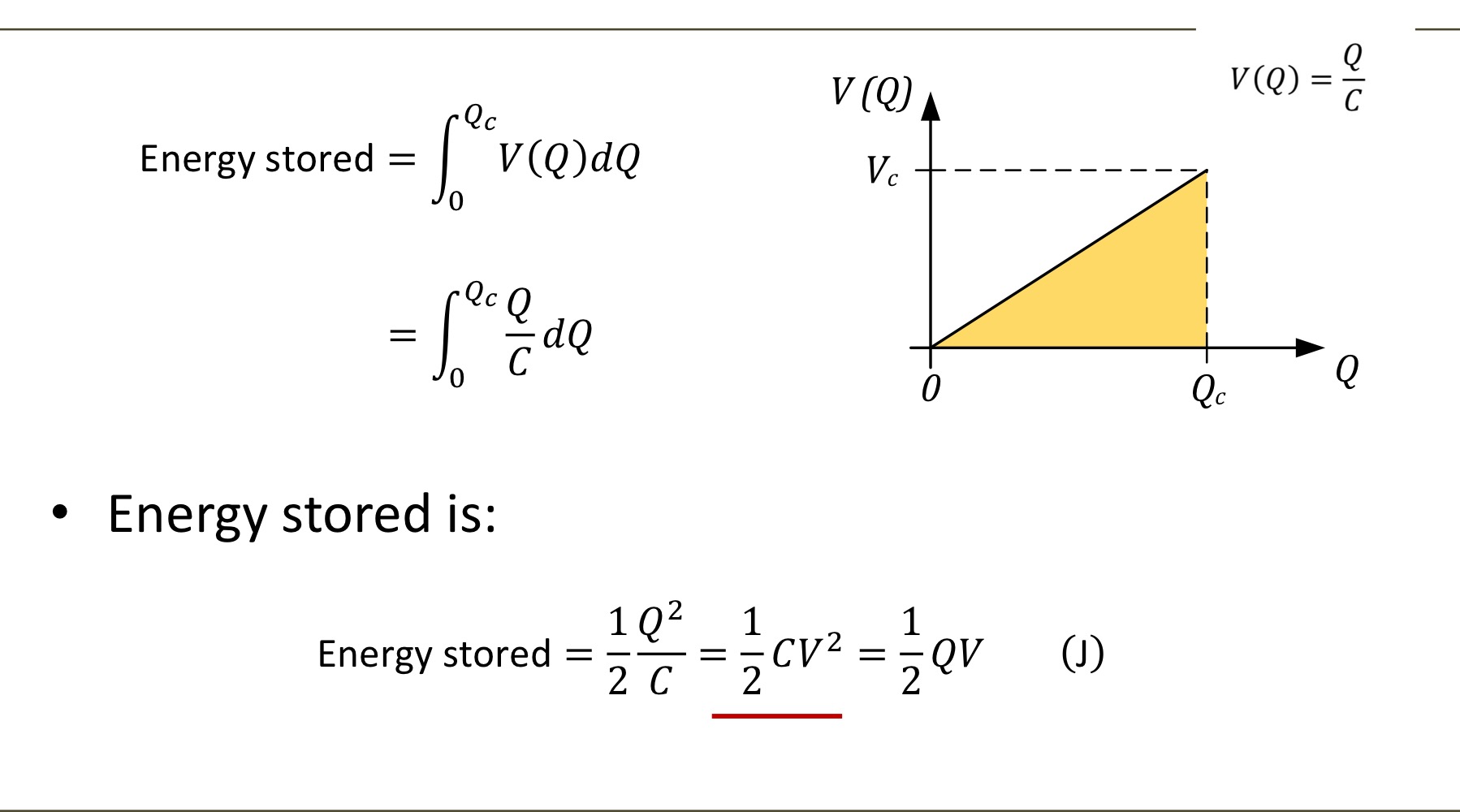
Energy stored in capacitor formulas
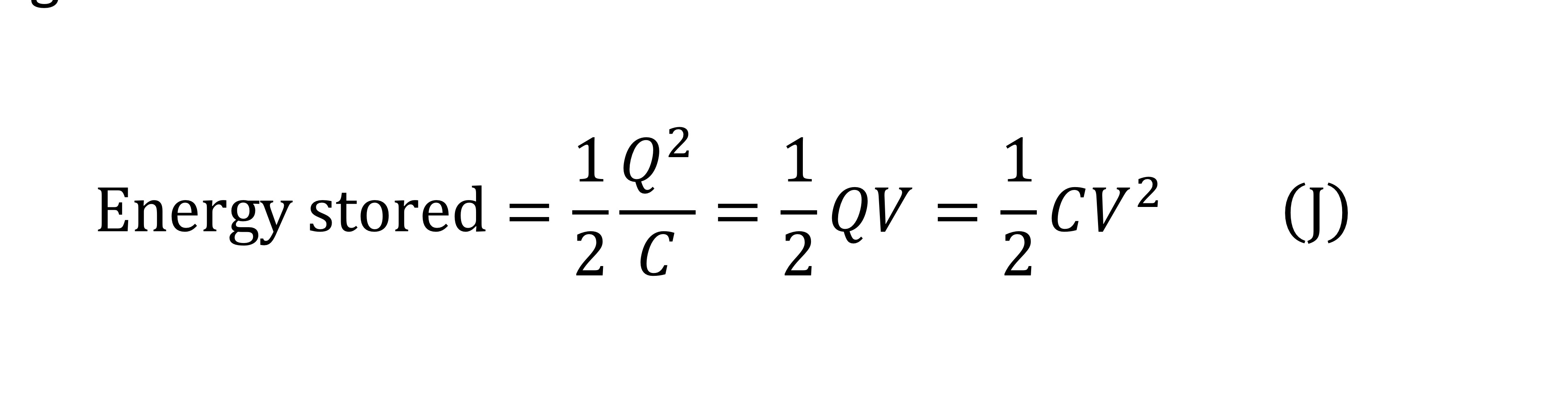
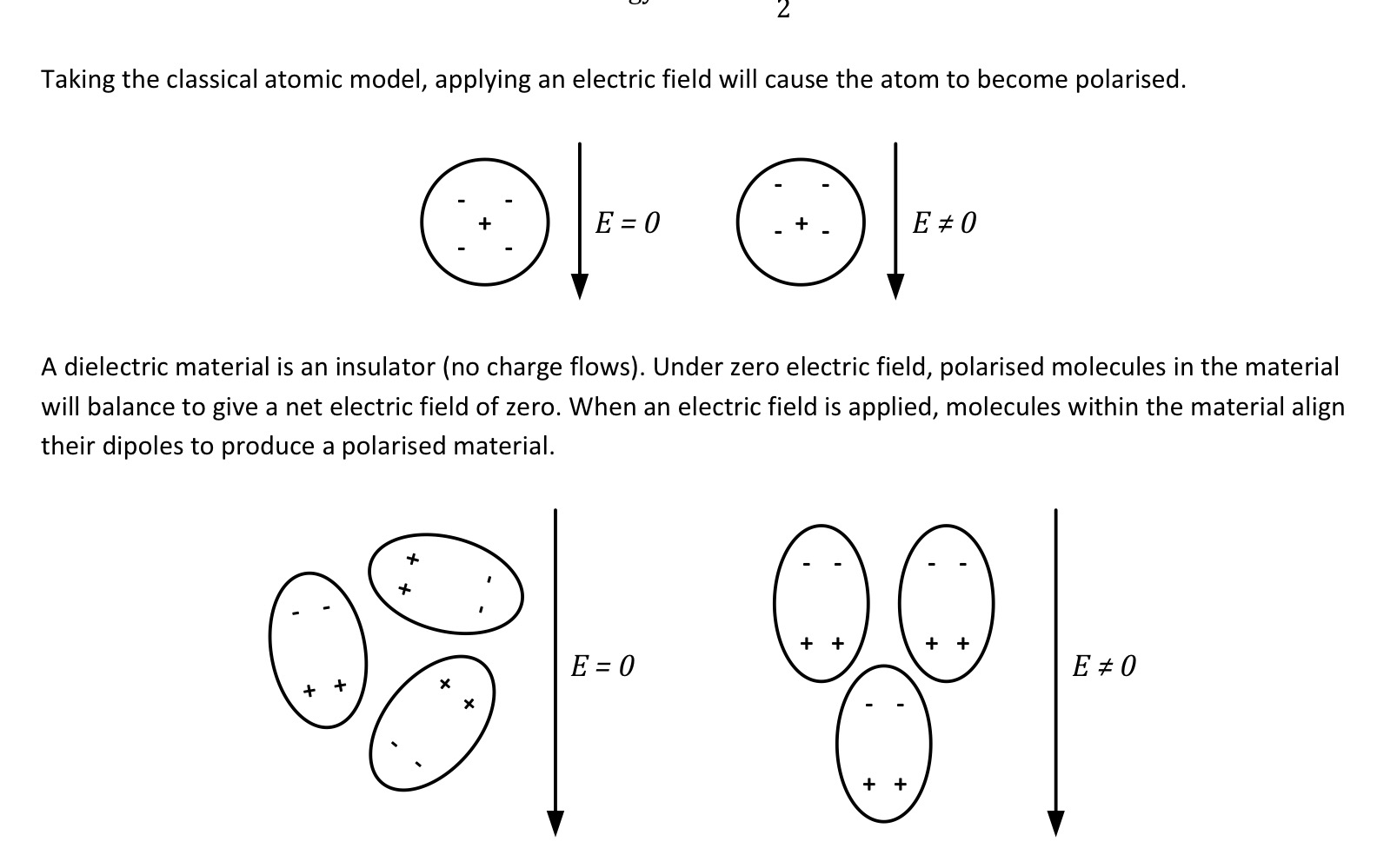
Why use dielectric?

What is dielectric material?
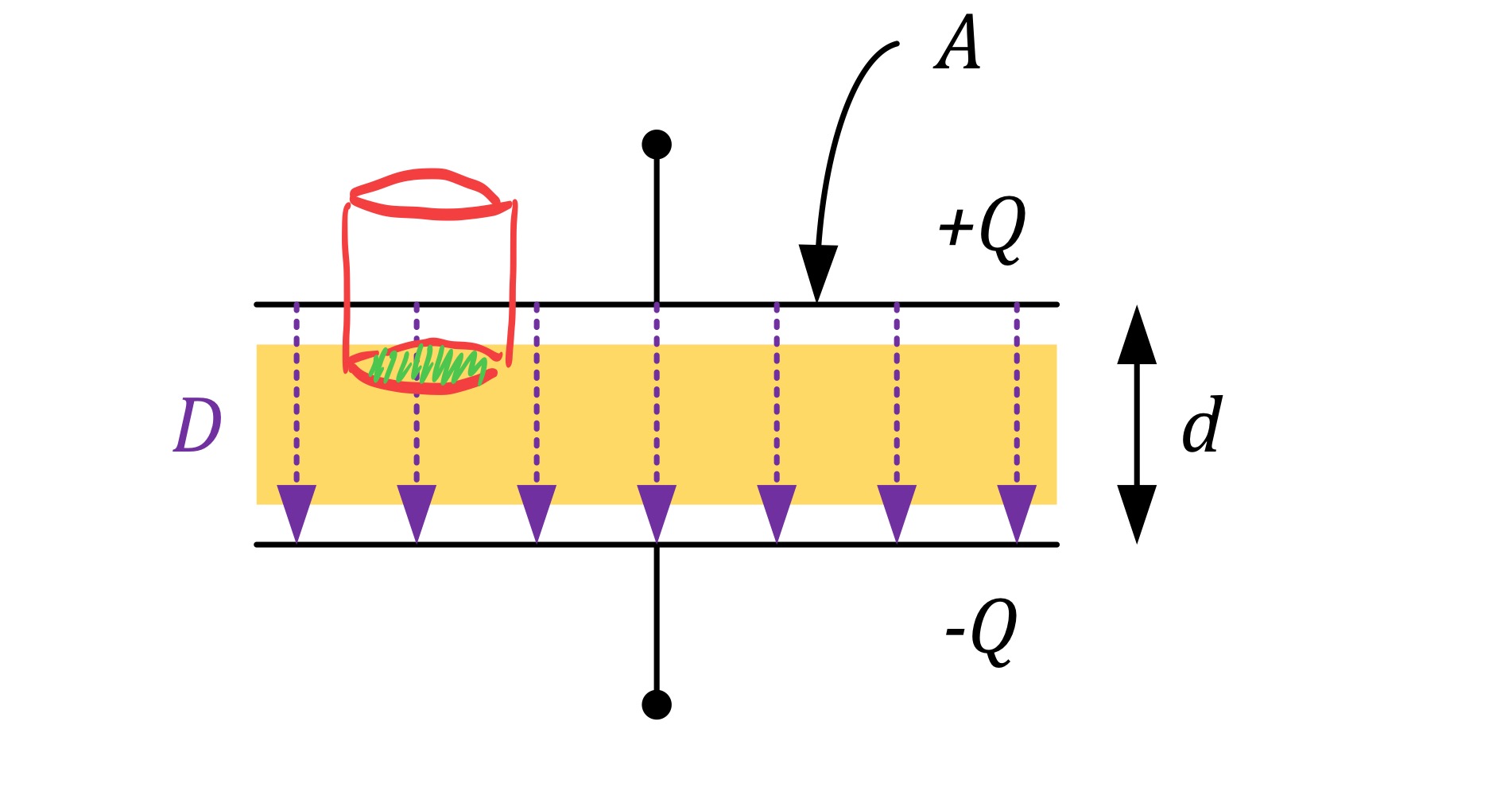
Assume that we have the same parallel plate capacitor as before. Now, the free space between the plates is replaced by a dielectric material of relative permittivity 𝜀𝑟 . The application of Gauss’ Law is not affected by the presence of a dielectric. A Gaussian surface is selected such that the area through which flux passes is 𝑑𝐴.

Common dielectric materials

Relationship between electric fields strength E and applied voltage V for parallel capacitor
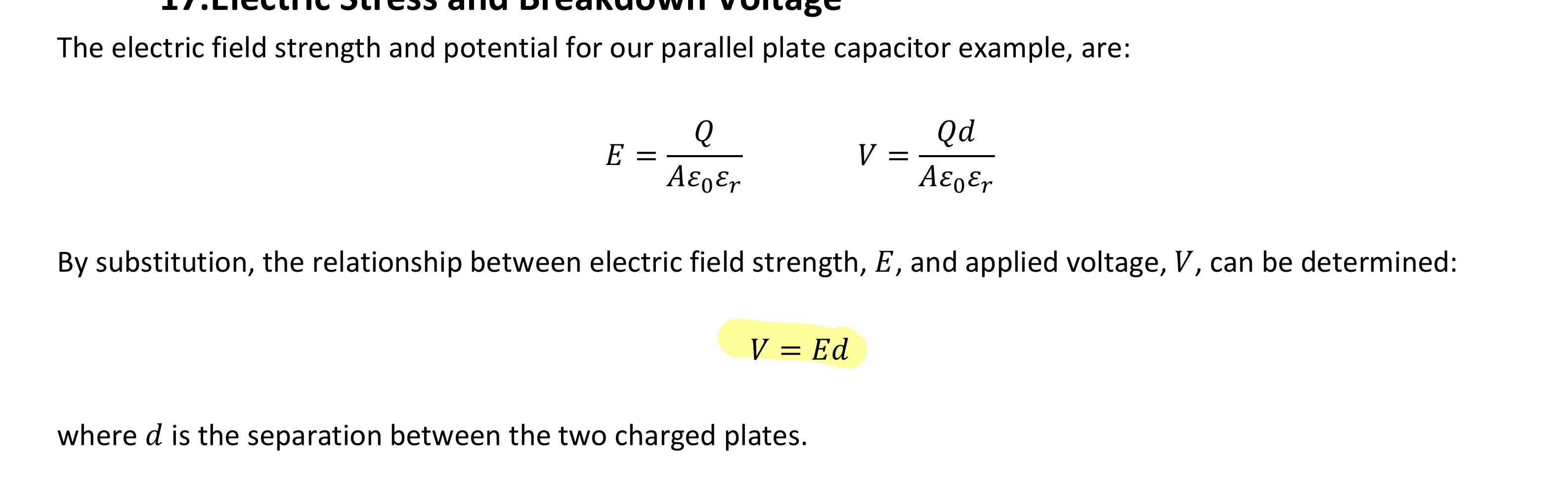
Dielectric strength, Eds
This is the maximum allowable electric field, above which the
material will break down and become a conductor.
What will happen to material if exposed an electric field E>Eds?
It will become a conductor
Breakdown voltage Vb
Maximum voltage that can be applied

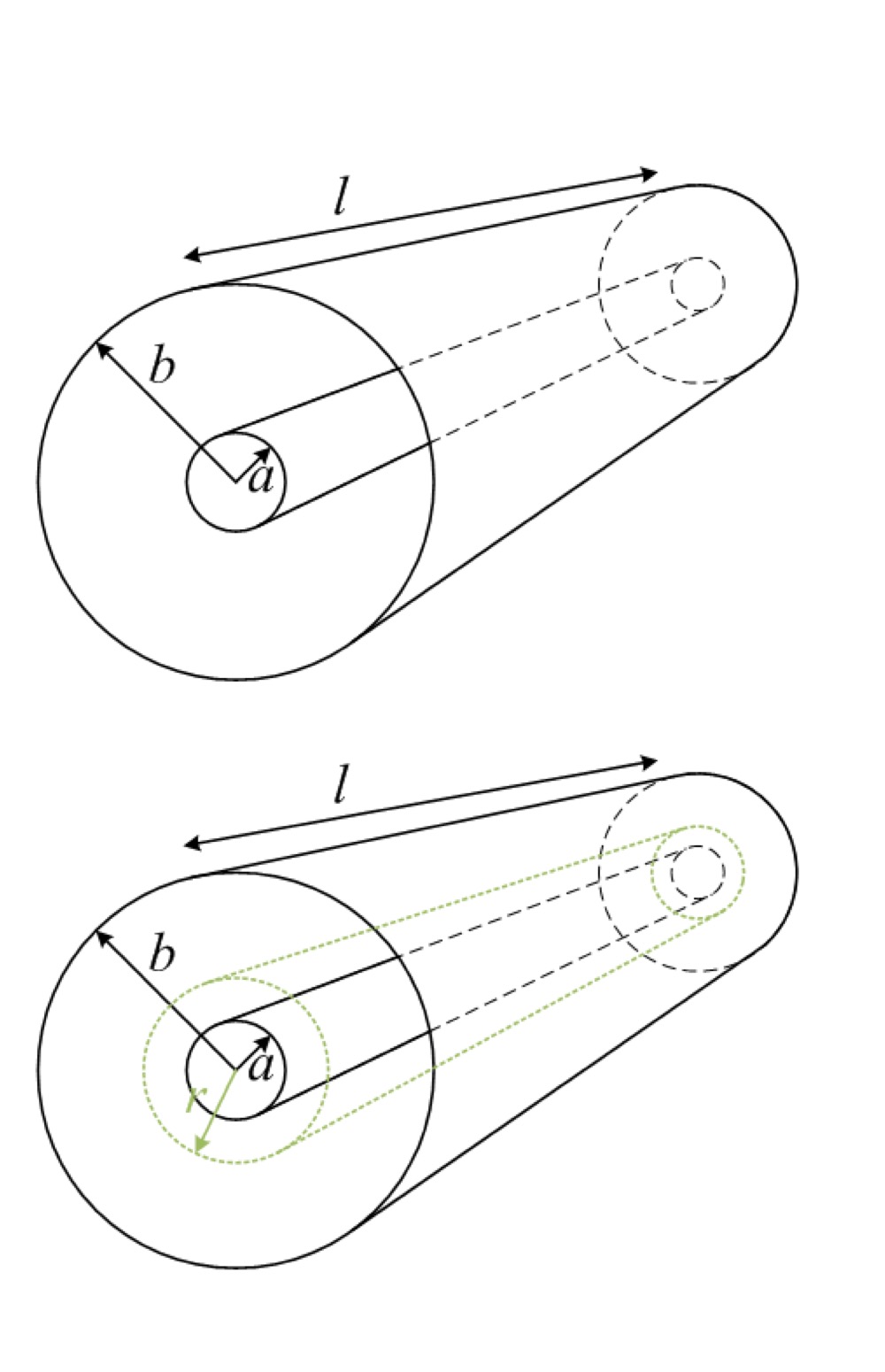
A coaxial cable is formed of a conducting core surrounded by a dielectric insulation (𝜀𝑟 > 1) within an outer conducting cylindrical sleeve. The inner conductor has a linear charge density +𝑞 C/m; the outer conductor has a linear charge density −𝑞 C/m. Use Gauss’ Law to derive an expression for the capacitance per metre, 𝐶𝑚 (F/m), of cable.

You have a mysterious closed box on your desk that says it contains several charged objects. You place a small positively-charged sphere near the box and the sphere moves away from the box. Wherever you place the sphere, it always moves away from the box.
True or false: The box only contains positively-charged objects.

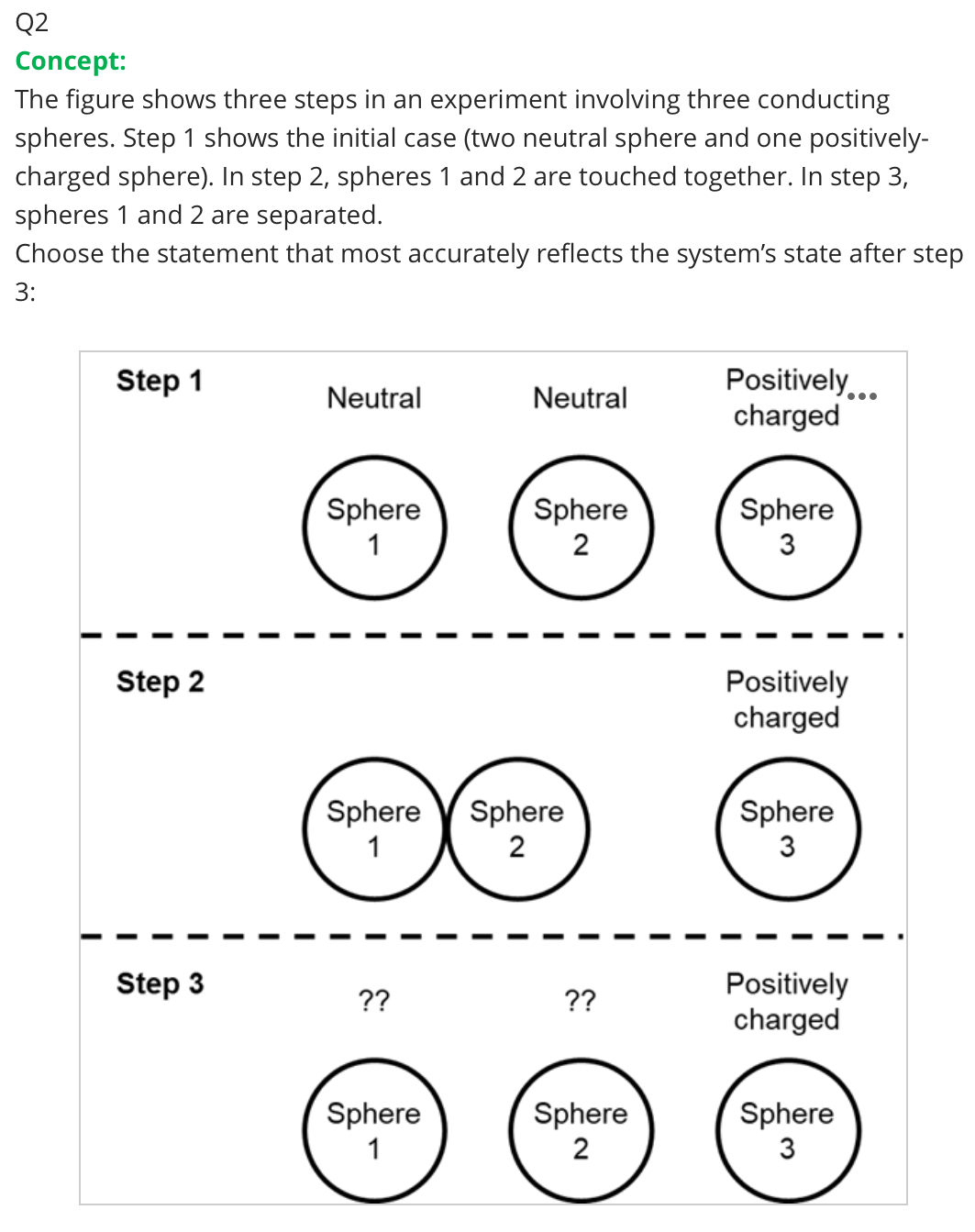
Both neutral
A spherical Gaussian surface encloses a point charge which sits at its centre. The point charge is then moved from the centre of the sphere to a point away from the centre.
True or false: The total flux through the Gaussian surface is unchanged.

A spherical Gaussian surface encloses a point charge which sits at its centre. The point charge is then moved from the centre of the sphere to a point away from the centre.
True or false: The electric field at any given point on the surface does not change.


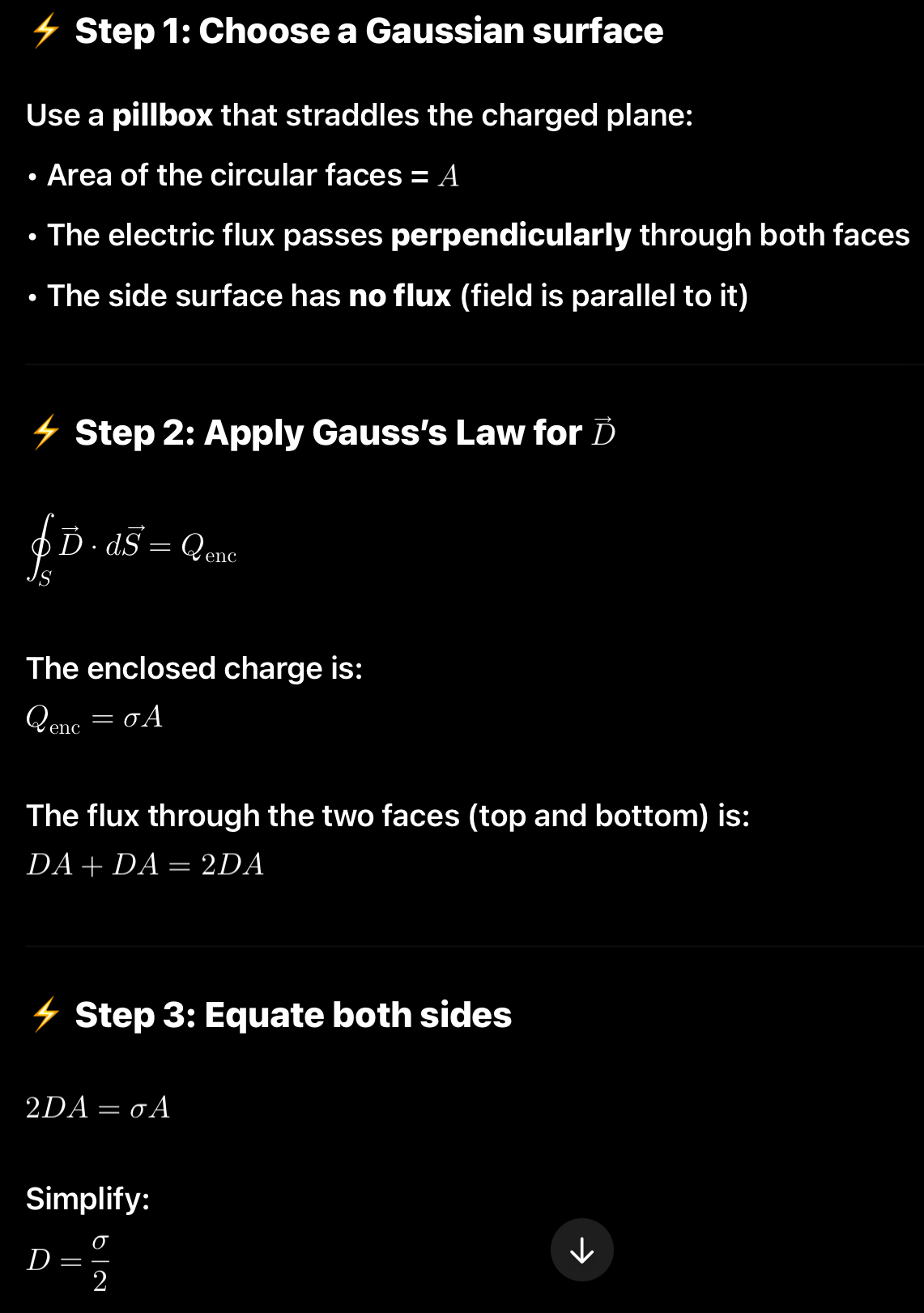

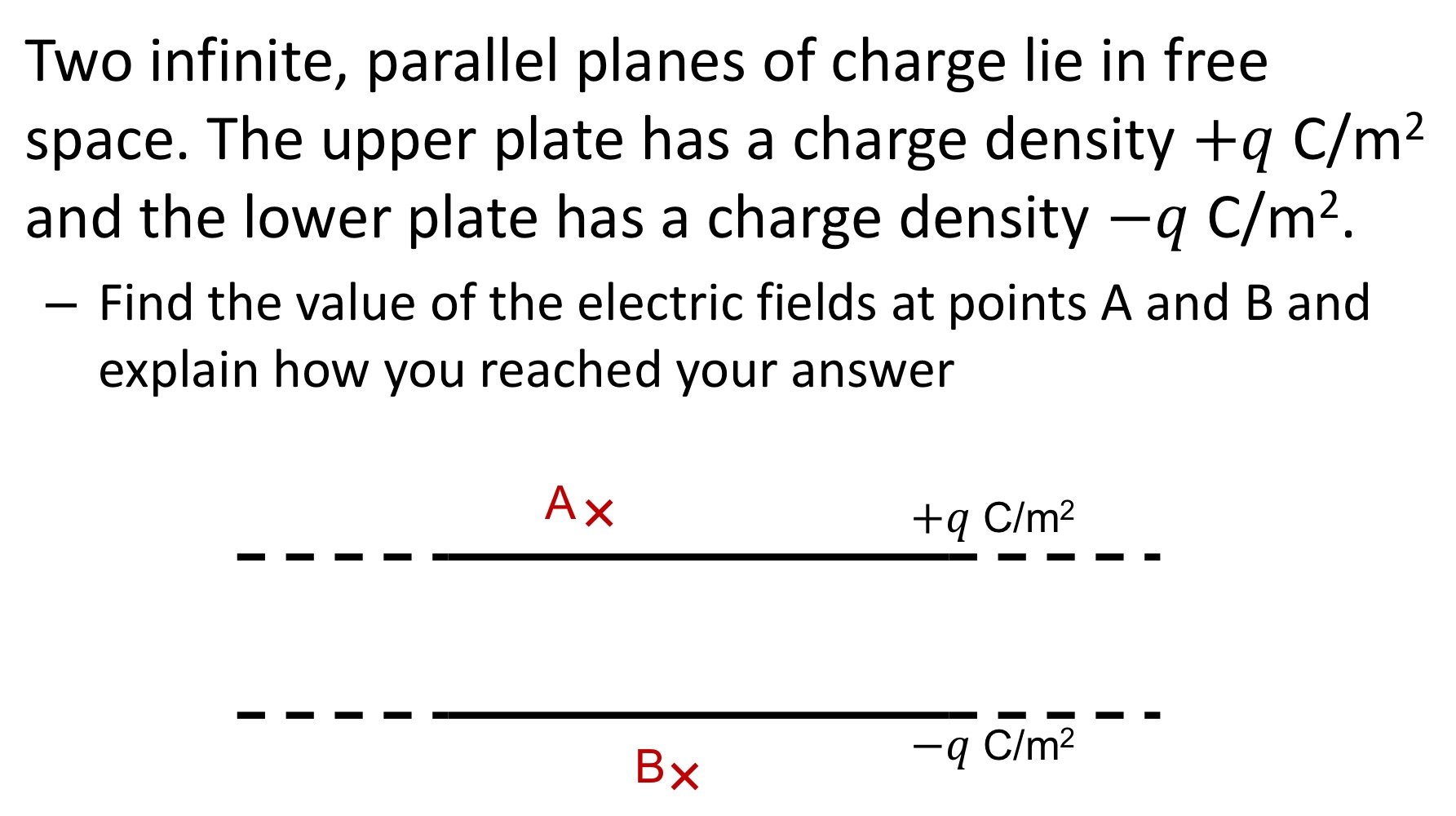
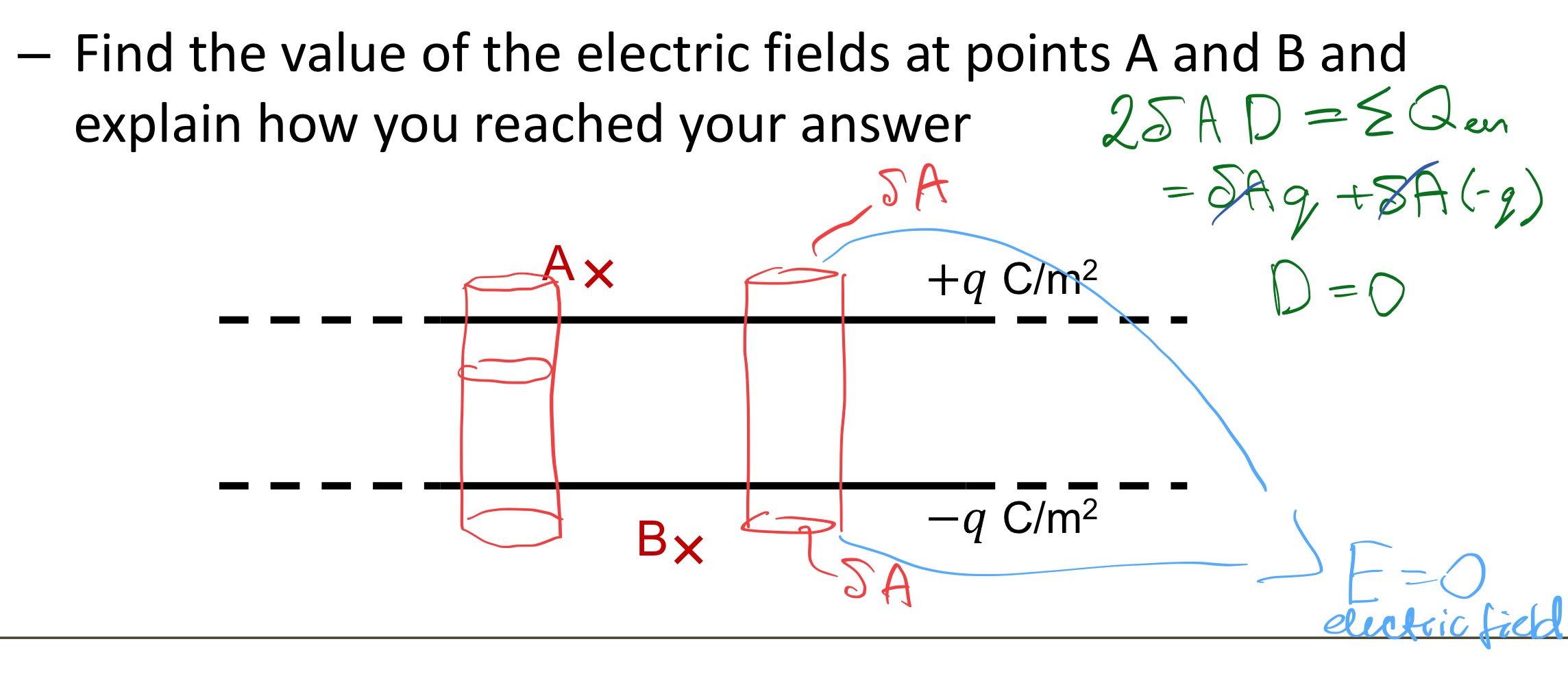
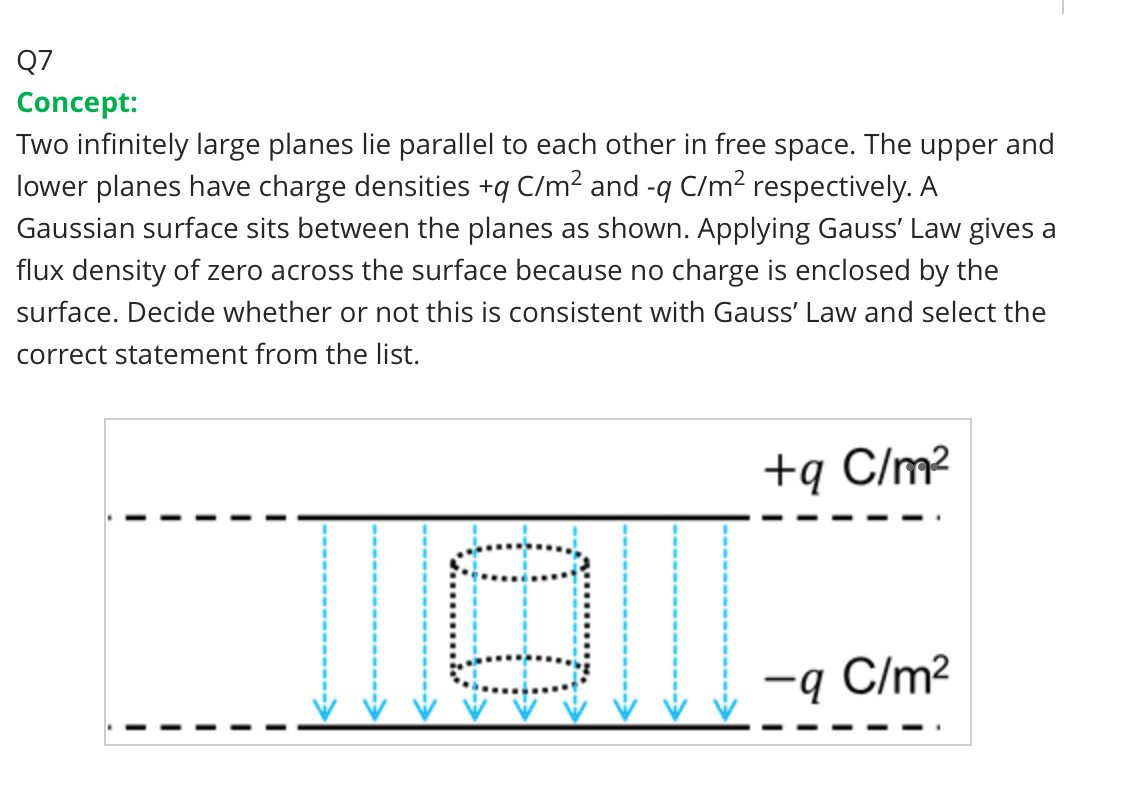
True or false: The electric flux density is constant and does not depend on distance from the plane.



2a instead of a

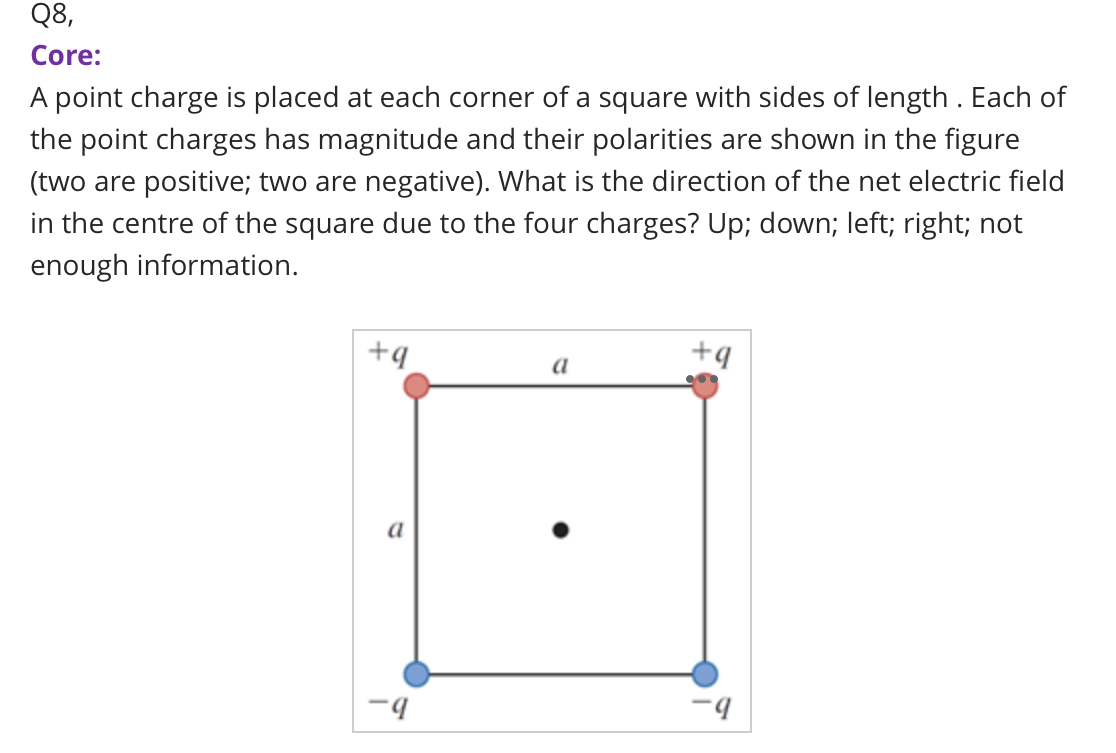


A point charge is placed at each corner of a square with sides of length . Each of the point charges has magnitude and their polarities are shown in the figure (two are positive; two are negative). What is the direction of the net electric field in the centre of the square due to the four charges? Up; down; left; right; not enough information. Two positive charges at the top and two negative on the bottom

True or false: The capacitance of an object varies with the amount of charge it holds.
FALSE: The capacitance of an object depends on its physical properties: dimensions and materials.
True or false: The flux density inside a parallel plate capacitor depends on the charge density on its plates.
TRUE: Applying Gauss’ Law for flux density to a charged system shows that flux density is a function of surface charge density (C/m2).
The two plates of a parallel plate capacity have area 𝑨, are separated by a distance 𝒅 and sit in free space. The upper plate has a total uniformly distributed charge of +𝑸 C; the lower plate holds a total uniformly distributed charge of −𝑸 C. What should you assume in order to apply Gauss’ Law? [Select all that apply; you must select only and all the right answers]
• The separation of the plates is small compared to the area of the plates.
• There is no fringing flux.
• The upper plate is positive.
• The electric field outside the capacitor is zero.
The separation of the plates is small compared to the area of the plates. ✓
• There is no fringing flux. ✓
• The upper plate is positive.
• The electric field outside the capacitor is zero. ✓
Note that the last point (zero field outside the capacitor) is closely related to the plate separate and the fringing flux.
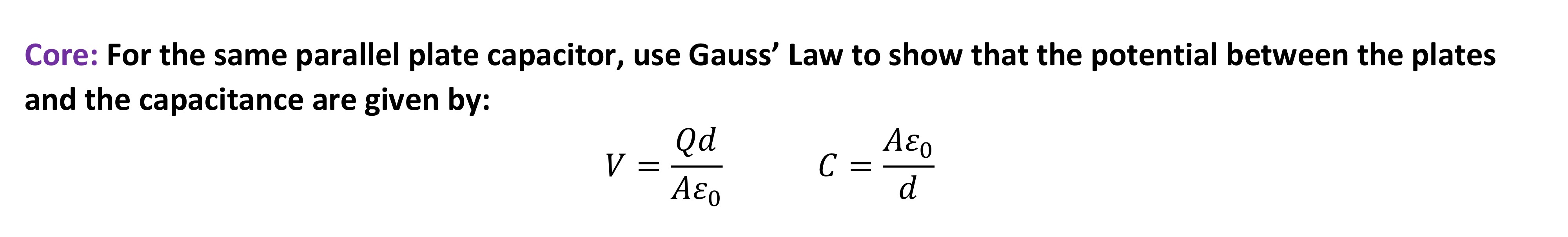

![<p>A parallel plate capacitor has two dielectric layers with different relative permittivity as shown. Apply Gauss’ Law to establish whether the electric field strength greater in layer 1 or layer 2. [Hint: Remember that Gauss’ Law for flux density can be applied without reference to permittivity]</p>](https://knowt-user-attachments.s3.amazonaws.com/2587921f-0347-426d-a618-4638fb5521b0.jpg)
A parallel plate capacitor has two dielectric layers with different relative permittivity as shown. Apply Gauss’ Law to establish whether the electric field strength greater in layer 1 or layer 2. [Hint: Remember that Gauss’ Law for flux density can be applied without reference to permittivity]


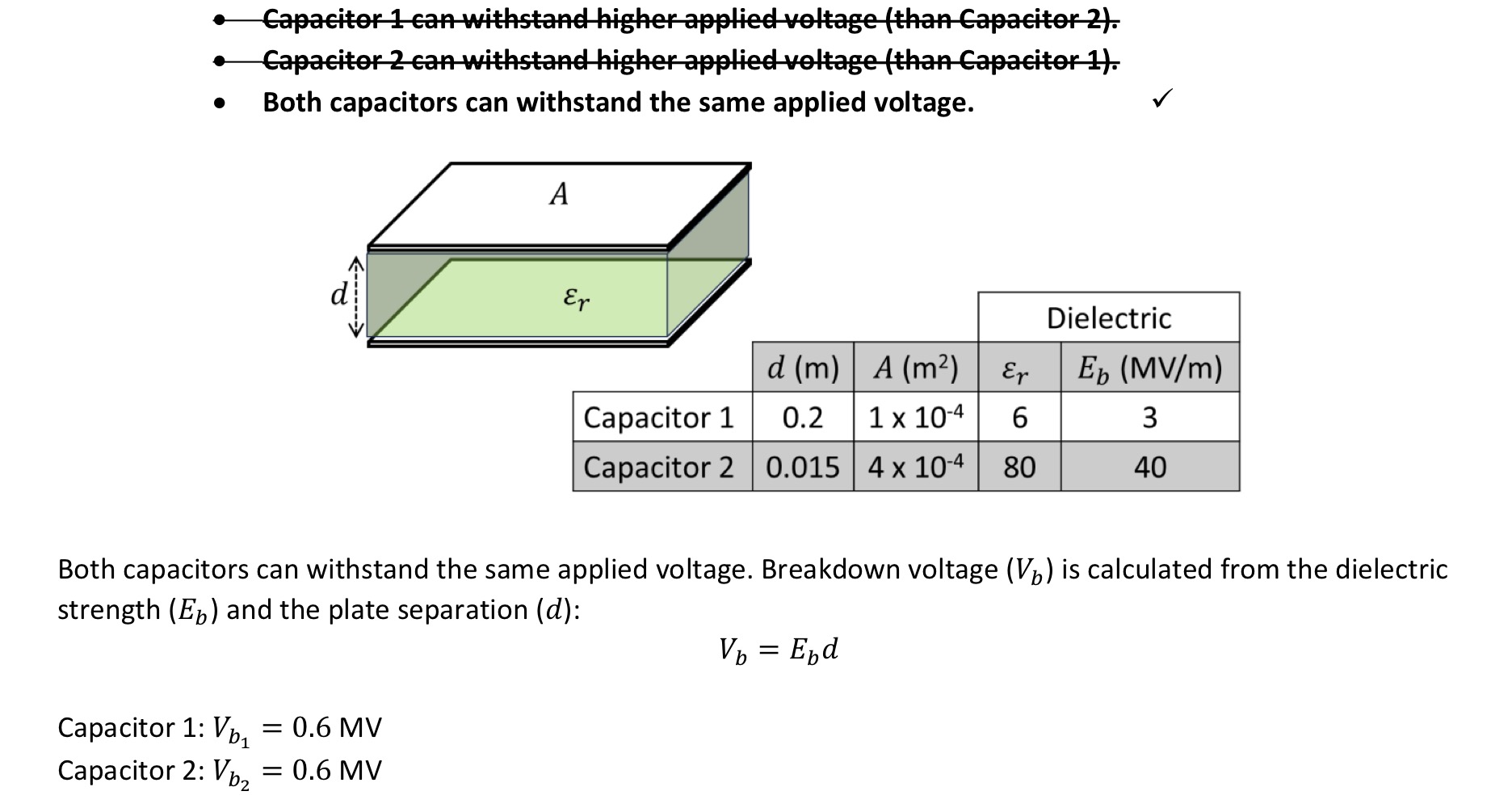
The properties of two parallel plate capacitors are given in the figure. Which statement is correct?
• Capacitor 1 can withstand higher applied voltage (than Capacitor 2).
• Capacitor 2 can withstand higher applied voltage (than Capacitor 1).
• Both capacitors can withstand the same applied voltage.
A 5 μF parallel-plate capacitor with circular plates is connected to a 12 V battery. After the capacitor is fully charged, the battery is disconnected without loss of any of the charge on the plates. A voltmeter is connected across the two plates without discharging them. What does it read? [Give your answer in V]

With the capacitor still disconnected from the battery, what would the voltmeter read if the plate separation were now doubled? [Give your answer in V]
Two parallel conductors sit in free space. Their currents flow in the same direction. Is the force between them attractive or repulsive?
The force is attractive when two parallel currents flow in the same direction.
Two conductors sit in free space at 90° to each other. True or false: In an ideal system, there is no force between the two conductors.
‘TRUE: The force between conductors is a cross product such that Lorentz force is 𝐹 = 𝐵 × 𝐼 𝑙. Placing the conductors at 90° to each other means that they do not interact and there is no force between them. This is an important consideration when high current cables are positioned close to sensitive measurement cables.