Permutations

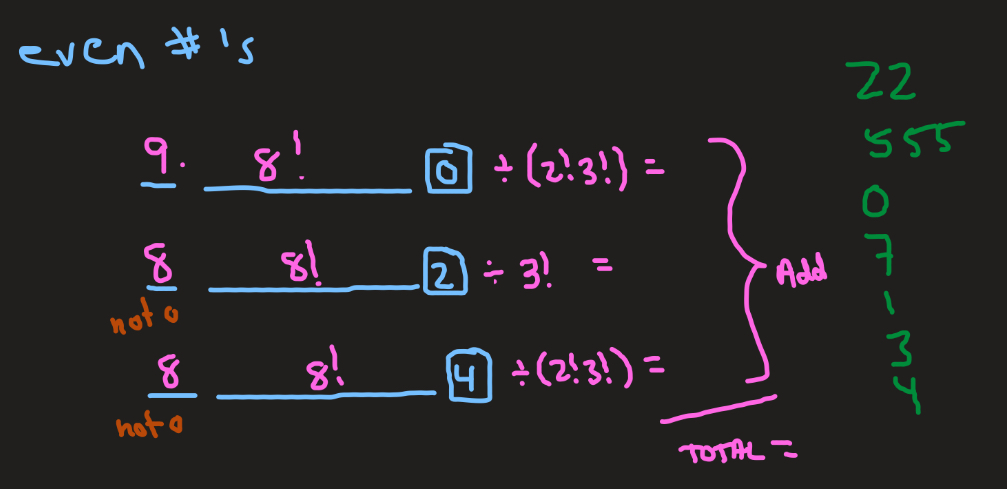
Given a scramble of numbers, how would I sort for ways to find all EVEN arrangements? Ex. 2555207134 (10#)

CASES ❕

1. If it ends in zero

9! (/ # of repeats as factorials if applicable )

not 10 since 0 is locked in

2. If it ends in other even digit

8 • 8! (/ # of repeats as factorials if applicable )

starts with 8 b/c ≠0 and we locked in an even number

Repeat for each unique even number as # repeat factorials will differ

Given a scramble of numbers, how would I sort for ways to find all START ODD and END ODD arrangements? Ex. 5199697610 (10#)

• Lock in the amount of odd # in slot 1

• Lock in the amount of one less odd # in the last slot since we used the first number

• Fill in the remaining middle with (total # - 2)!

• Divide by repeat factorials if applicable

6 • 8! • 5 /2!3!

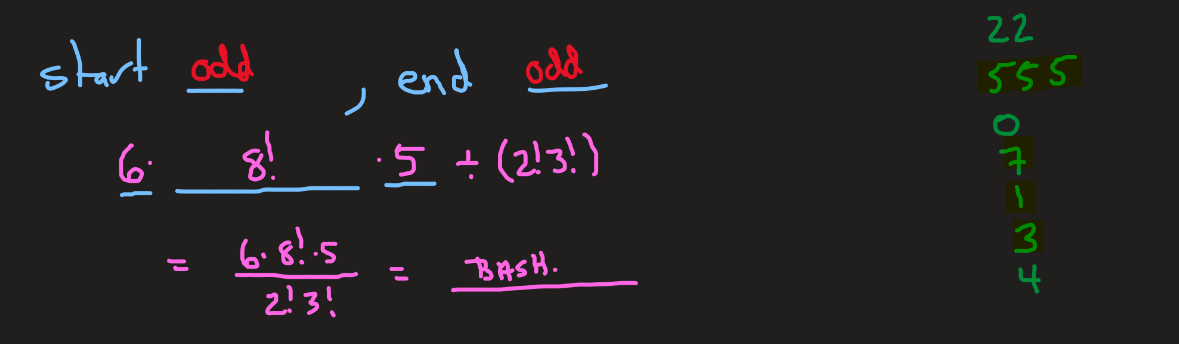
Given a scramble of numbers, how would I sort to find the ways a set of numbers is LOCKED IN? Ex. 5199697610 (10#) → lock in “7134”

• Consider “7134” as ONE block, which reduces the total number of digits by 3 (10-3=7)

• First slot cannot be 0, so reduce count by 1

• Fill in remainder slots (don’t forget you have 1 extra since you can include 0)

• Multiply by the # of ways inside the block can shuffle

• Divide by repeat factorials if applicable

(6 • 6! /2!3! ) x4

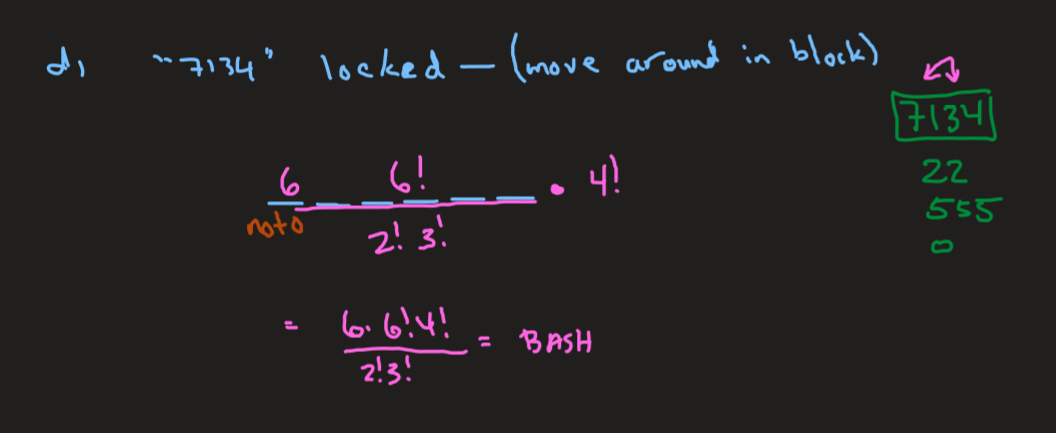
If I have a circle of people, how many unique arrangements would I have? Ex. 8

8! / 8 = 7!

Divide by the # of people to remove keeping the same people beside each other

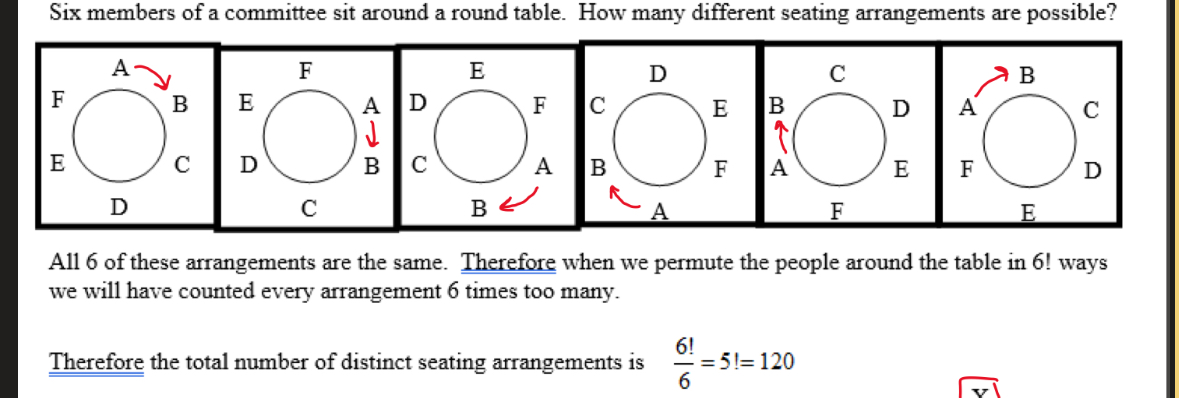
If I have a circle of people, how many unique arrangements would I have where X and Y are NOT TOGETHER? Ex. 8

• Make X and Y a block to calculate ways they are together: 7!/7

• Multiply by 2 for shuffling: 7!/7 ×2

• Take total of arrangements 8!/8 and SUBTRACT where X and Y are together: 8!/8 - (7!/7 ×2)

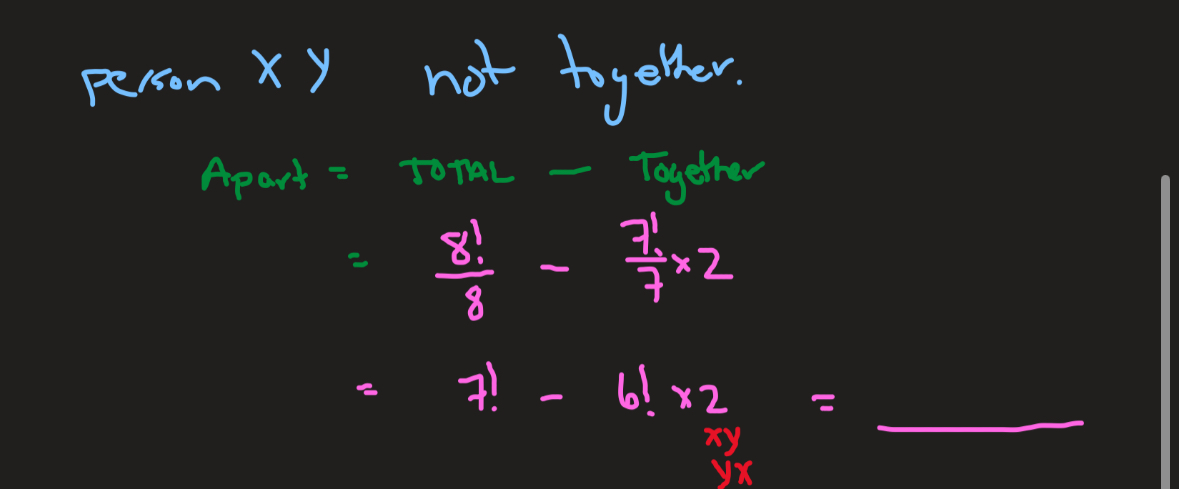
Given a set of letters, how can you find the # of arrangements you can make which start with a vowel and end with a consonant? Ex. “ALGEBRAICALLY” (13 #)

• Lock in the # of possible vowels at the start

• Lock in the # of possible consonants at the end

• Decrease total # of letters by 2 to account for the used slots and fill in the middle

• Divide by repeat factorials if applicable

5 • 11! • 8 / 3!3!

Given a set of letters, how can you find the # of arrangements you can make which have G and E TOGETHER? Ex. “ALGEBRAICALLY” (13 #)

Make G and E a block which decreases total # of letters by 1: 12!

• Multiply by 2 for shuffling: 12! ×2

• Divide by repeat factorials if applicable

12!/3!3! x2

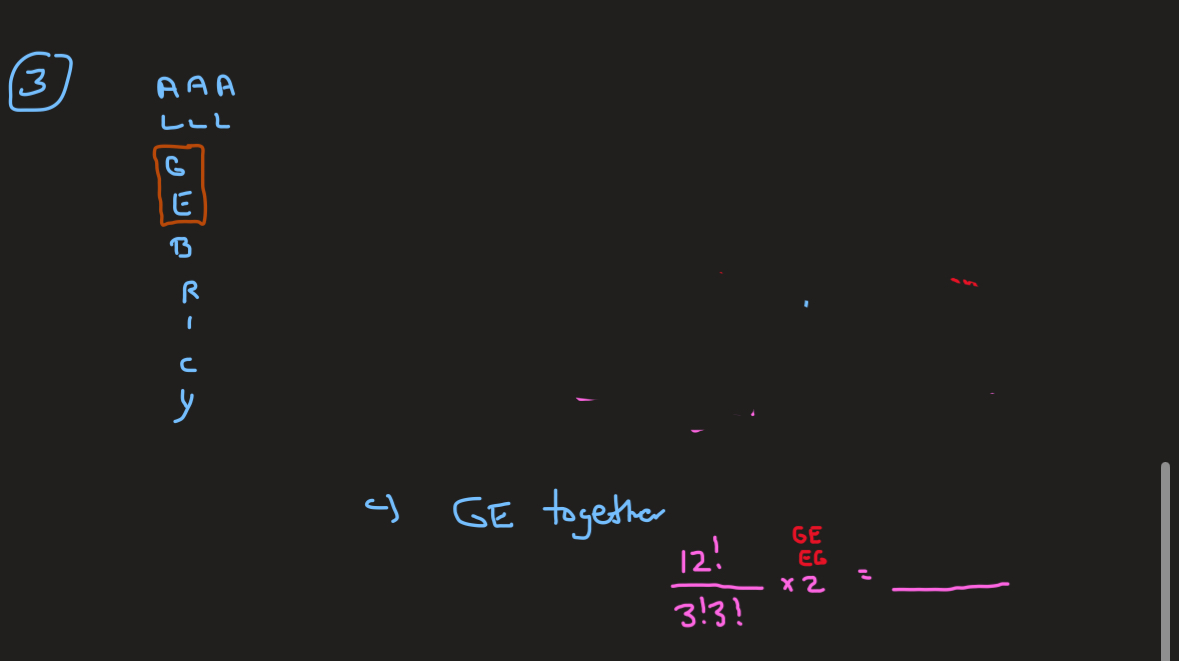
Given a set of letters, how can you find the # of 3 LETTER arrangements? Ex. “ALGEBRAICALLY” (13 #)

CASES ❕

1. No repeats

9 • 8 • 7

for A L G E B R A I C Y (9 letters)

2. Pairs

• We use ONE pair leaving us with 1 excess pair + 1 extra so 10-2=8 letters to choose from

• Break into # ways the pair can appear

❌❌✅ where ✅= # leftover (8)

❌✅❌

✅❌❌

8•8•8

• Multiply by 2 because of the excess pair

(8•8•8)x2

3. Triple repeats

Only 2 possible options: AAA, LLL

❕ THEN ADD ALL CASES TOGETHER ❕

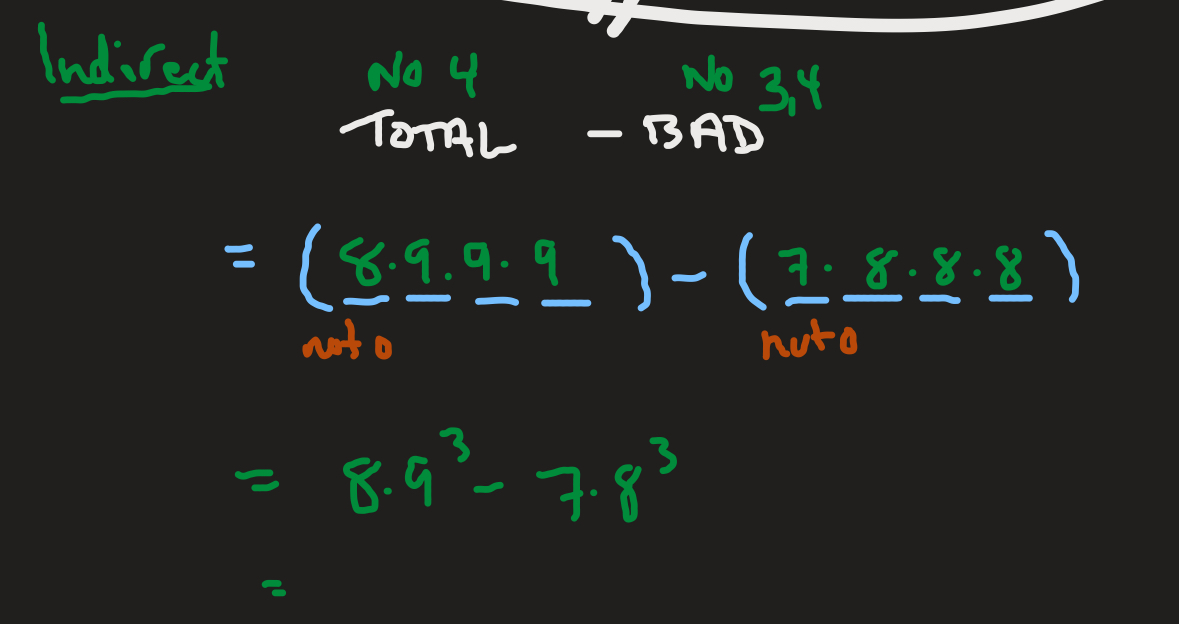
How can we find the amount of 4 digit arrangements that include a number and exclude another? Ex. include 4 and exclude 3

Indirect method: Total - bad

0→9= 10 numbers

Total with no 4 = 8 • 9 • 9 • 9 (cannot start with 0)

Bad with no 3 or 4 = 7 • 8 • 8 • 8 (cannot start with 0)