Module 5: Multiple Regression Assumptions

In-person lecture covers 50% of content

Explain the underlying assumptions of regression*

Regression assumptions are actually made about the

Residuals

• I.e. The e in the regression equation

Why do we test assumptions on the residuals rather than the data?

Because we cannot do anything directly to the residuals (error) as it is what is left over after the line

Think: If there is a lot of error, our model probably sucks. We’re running the assumption tests on the residuals because if the error is too crazy, then we might not be measuring the right population or our model just doesn’t work.

Assumptions not met = model is shit

Regression (linear) will still ‘work’ for nonlinear relationships but….

Interpretations of parameters on face value may be meaningless

Describe the assumption of normality

Residuals (errors) are normally distributed around a mean of 0

• Centred around 0, being the mean score

• Assumption of regression

Think: If everyone did a stats exam and the error was not normally distributed with a mean of -5, it might suggest that the test itself was too hard and therefore results can’t be interpreted as the knowledge of 3rd year stats students. Maybe the test was for honours students.

Homoscedasticity

Constant variance of residuals across predicted scores

• When residuals are correlated with predicted scores

• Random error is observed

• No important predictors have been left out

• Indicated by rectangular shape

• Assumption of regression

Independence of errors

The residuals are uncorrelated with Y

• If it is correlated with Y then it is not error, and it has tapped into a another construct that was not considered.

Think: Imagine you are trying to predict house prices (criterion) using variables of square footage, number of rooms and year the house was sold (predictors). A factor that has not been considered is inflation, economic state and demand for housing which would influence price and likely cause error stemming from the year the house was sold. If you plotted error/residuals for the year the house was sold, you would see a positive association between error terms and house price, in that as year increased, so the did the price of houses and thus the error margins increased.

Linearity of the relationship

Regression models are linear (think: line of best fit), therefore you can’t interpret data that is not linear.

• Assumption of regressions

Assumptions for checking residuals

• Normally distributed

• Homoscedasticity

• Independence of errors

• Linearity

The regression equation of Y = Y’ + e states that the actual score from a regression is the sum of the predicted score plus the error.

Explain what the error refers to.

The residual

• Variance that is not explained by the model

• Not everyone’s scores are going to be the same

• The only way this would be possible would be if the data had a perfect correlation (± 1).

Think: Someone with perfect knowledge of the exam content but missed 1 slide in the mini lecture, so they got that one question wrong.

If the regression equation has underestimated the actual score, the residual will be…

Positive

The the regression equation has overestimated the actual score, the residual will be…

Negative

In a multiple regression, should you use residual e or Zresid to run assumptions?

Z scores

• Converts them all to the same unit therefore residuals are proportionate to each other

• Use SPSS syntax

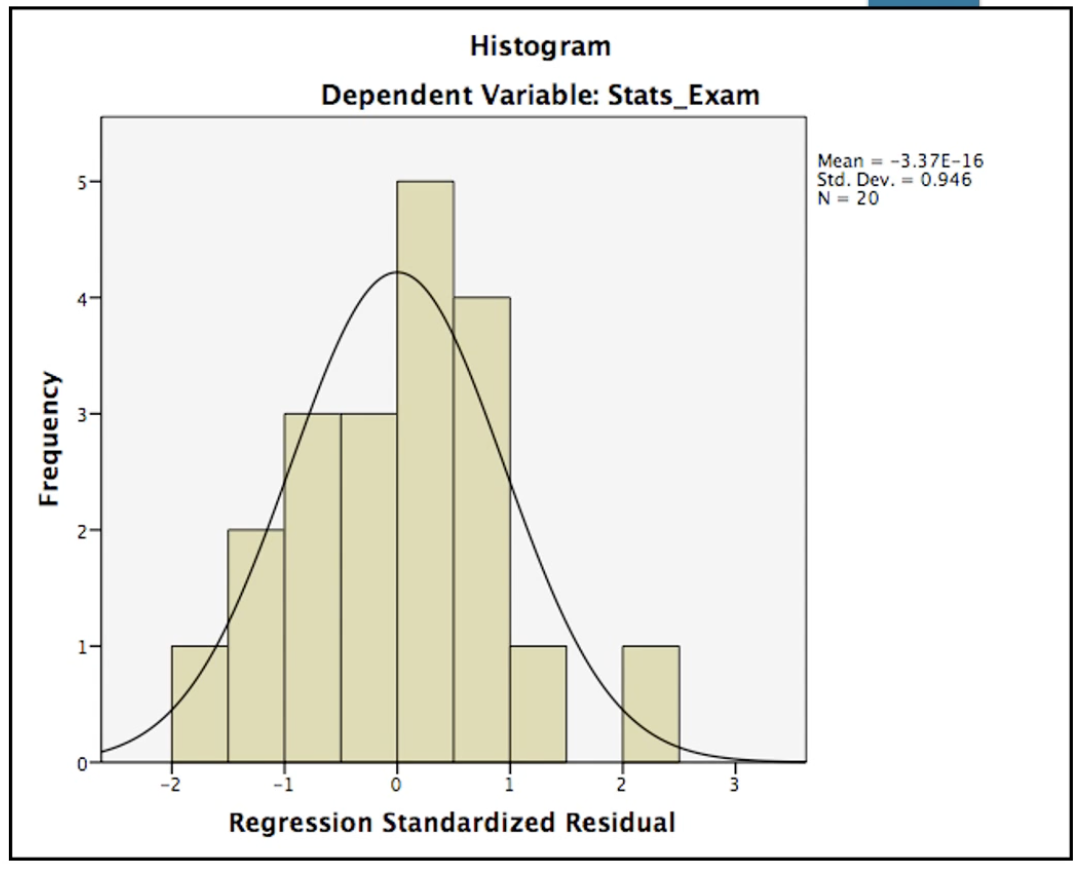
What assumption is being tested here, and has it been met?

Normality

• Yes - residual means are centred around 0

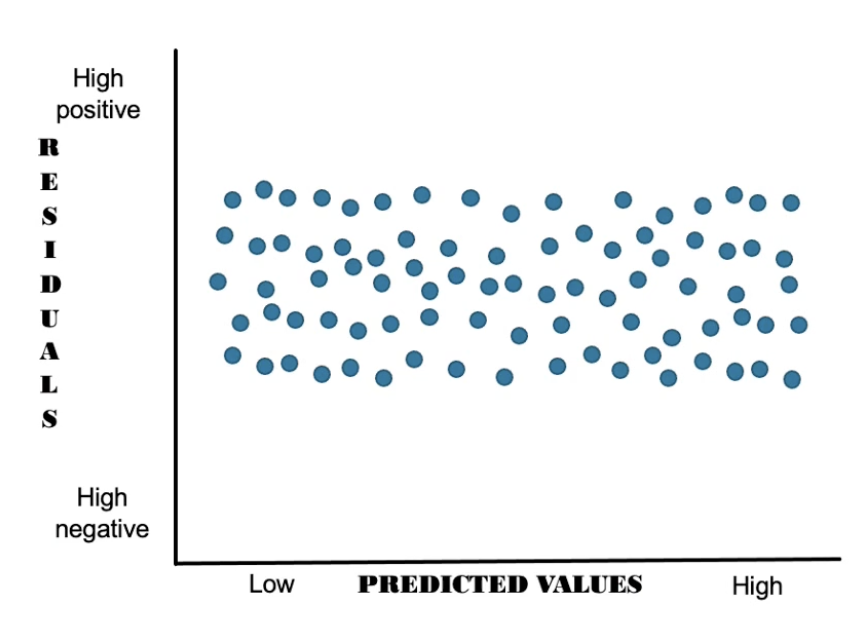
What assumption is being tested here, and has it been met?

Homoscedasticity

• Yes - takes on a rectangular shape

• Small variance around zero on the Y axis (in the middle) and evenly scattered above and below

Think: Homoscedaddle = skinny rectangle centred at 0

In homoscedastacity, the larger the range on the Y axis…

The worse the prediction

What does a non-significant test of homoscedastacity look like?

A funnel or a fan

• Shows the distribution of residuals across the range of predicted values of Y is not even

• May suggest there is worse prediction at low/high predicted values of Y

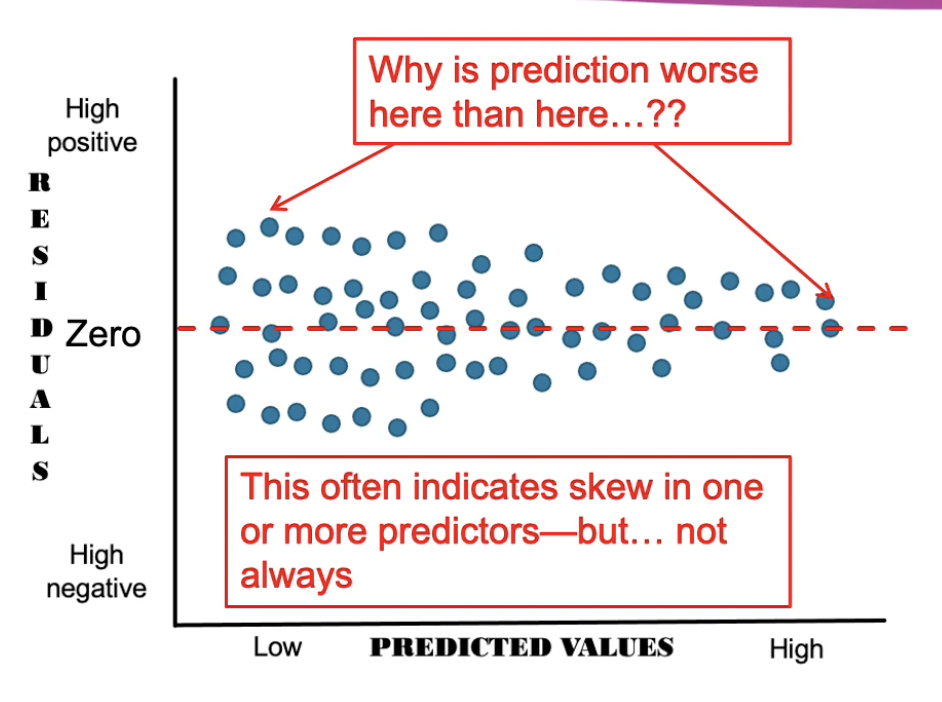
Interpret this

Homoscedastacity is not met

• Funnel shaped

• The model has greater predictive value at the higher predicted values of Y, as indicated by the lower variability around zero on residuals (Think: narrow rectangle)

• The model has less predictive value for lower scores of Y and there is more variability of residuals at this point

If assumptions of regression are not met, what approaches can be taken that don’t involve using a whole different statistical procedure?

• Removing outliers

• Apply transformations to the data

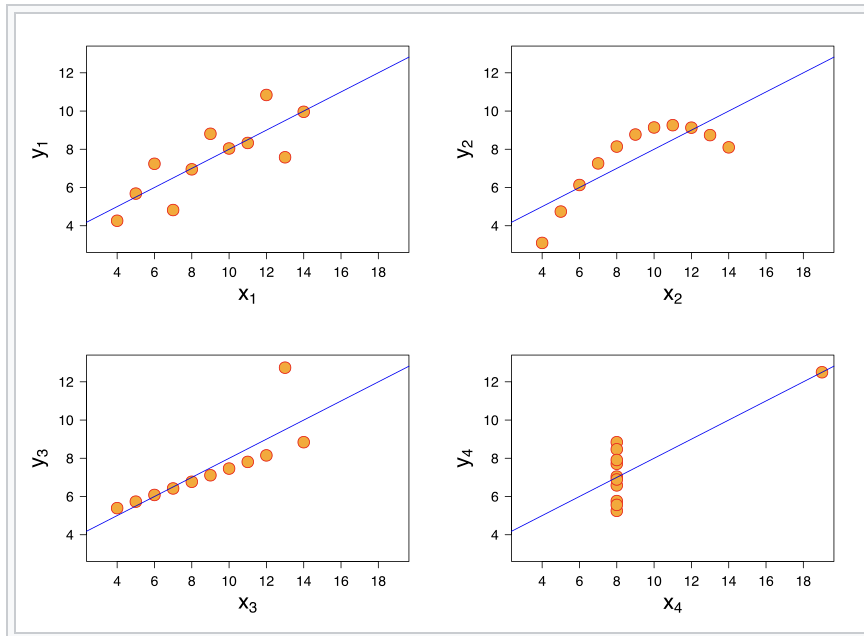
Anscombe’s Quartet

Refers to 4 datasets that illustrate how characteristics such as non-linearity and outliers can seriously distort our interpretations of correlation and regression statistics.

• Show that we cannot have confidence in the numerical statistics without examining the visual form of the underlying data

• Also shows the importance of looking at the data visually instead of just chasing assumptions as we need to know why a dataset is distributed that way.

The 4 datasets have identical descriptive stats (to 1 dp), though one is linear, one has outliers, curvilinear and one is non-linear with an outlier.