MHF4U

How to determine if a relation is a function

1. Check if each x-value only has one y-value

2. Vertical Line Test (best applicable to graphs)

Absolute Value

the horizontal distance between the origin and the number. It is always positive

Graphing Absolute Value on a number line

1. Plot the negative and positive value on the number line

2. Use an closed circle if it is including the number and open circle if it is not

3. Create a statement of the range of numbers in which it applies to

Asymptotes for exponential functions

The parent function has a horizontal asymptote at y=0 but if there is a vertical shift in the function, the shift value is the new equation of the asymptote

Piecewise function

a function that uses two or more rules on two or more intervals. Can be discontinuous or continuous

Graphing piecewise functions

same thing as graphing regular functions but make sure you look at the intervals b/c a new function may start

Average Rate of Change

- delta y/delta x or y2-y1/x2-x1

- the secant line represents ARC

- express as a rate

Secant line

- ARC

- Passes through two points in a graph

Velocity ARC

Change in distance/change in time

Tangent line

- touches the graph at only one point

- represents IRC

How to find IRC

- Graph: if given a graph, try to draw tangent line and find the slope to find the IRC

- difference quotient

- express as a rate

Difference Quotient

h = 0

How to determine whether a point is a min/max?

1. Check if the IRC = 0 at the point

2. Check if the IRCs of the two points on the left and right side change from negative to positive (minimum) or positive to negative (maximum)

How to draw speed/time graph

1. find the slope of each interval on original graph

2. graph with horizontal (straight)/exponential lines (curved) for the entire duration of each interval (some overlap may occur

Snowball question

1) If given the radius, you are finding the volumes for the given radii and calculating ARC of those volumes (numerator)

2) If given the volumes, use the volume formula to find the radii and calculate ARC of the radii (denominator)

How to find a k value in a piecewise function

1. find the points at the end of each range for the two connecting functions

2. try to equate two functions within the piecewise function

3. solve for k

Polynomial Functions

- has addition or subtraction of terms

- all exponents are positive whole numbers

- no division of terms or square roots

- leading coefficient is coefficient on the variable with highest degree

- the degree is the highest exponent

- domain is ALWAYS all real numbers

Finite differences

determine what type of polynomial it is

constant...

first differences = linear

second = quadratic

third = cubic

fourth = quartic

fifth = quintic

Turning Point

a point where a function changes from increasing to decreasing or vice versa

Increasing function

function increase from left to right

Decreasing function

function decreases from left to right

End behaviour

what happens to the y values as x approaches negative or positive infinity

- sign of leading coefficient determines end behaviour

- even degree functions have end behaviours in the same direction and odd degree functions have end behaviours in the opposite direction

- use test values in between x-intercepts to graph behaviour of function

Multiplicity

the number of times a factor appears in a polynomial function

- the degree/order

Even Multiplicity

means it is a turning point

Odd Multiplicity

means the function crosses through the point

Determining equation of polynomial from graph

Use the factored forms of the function:

y=a(x-r)(x-s)(x-t)

Solve for a using a point given and intercepts

Even function

satisfies the equation

f(-x)=f(x)

- symmetrical in y axis

Odd function

satisfies the equation

-f(x)-f(-x)

- symmetrical in origin. when turning it 90 degrees you get the same function

How to find the x-intercept of a polynomial

1. set y=0

2. bring over the constant if any or factor

3. find x

How to determine if a function is even or odd

see if they satisfy the equation of an odd or even function. if it is neither then the function is neither even nor odd

When graphing cubic functions...

make sure you make it clear where the origin point is!

How to describe a polynomial

- degree

- intercepts

- turning points

- end behaviour

When can a polynomial be even and odd

at y=0

when can a polynomial have symmetry in the x axis

y^2=x

How to use remainder theorem

if the divisor is linear, take the b term (constant), flip the sign and evaluate the function for that number

ex: x^2+x+1 divided by x+1

plug in f(-1) into function and you'll get the remainder

if the linear function has a coefficient, flip the sign of the negative and divide by coefficient

ex: divisor: 2x+1

plug in f(-1/2)

Long Division

- works for any polynomial

- must be completed with a division statement: dividend = divisor x quotient + remainder

- add fillers when there's missing terms to make it easier

- ex. x^2 + 1... add x^2 +0x +1

Synthetic Division

- only works for linear factors

- take the p term or q/p term and switch the sign, then take the coefficients of the dividend and multiply by p term and add my next coefficient. repeat

How to find divisor when given dividend and quotient

Divisor = (dividend - remainder)/quotient

Factor Theorem

- if the leading coefficient is one, find factors of p value and trial and error til you find a factor that equals 0

- one you find a factor, use synthetic division to find the other factor

- factor the result from synthetic divsion

- finish with a statement

Sum and Difference of Cubes

(x^3-y^3) = (x-y)(x^2 +xy +y^2)

(x^3+y^3) = (x+y)(x^2-xy+y^2)

Cardboard Squares Question

1. set up volume formula (plug in volume, length, width, height

2. length and width should be -2x and height is x

3. make equation =0

4. expand and find roots using factoring or quad equation

Solving polynomial inequalities

- find roots

-plot them on number line

- test numbers in between to see which areas are pos/neg

- use set/interval notation to write final answer

Finding 2 missing variables with given the factor and remainder

- use remainder theorem to sub in x and y value given

- create 2 equations for unknowns

- use substitution (subtract two equations) and solve for one variable

- sub in one known value to get the unknown

How to graph reciprocal of a function

- make a table of values for the original function

- for the reciprocal values, it is determined by y=1/x

OR

- find any holes

- determine all asymptotes

- determine end behaviour

- find vertex if necessary

- find intercepts

Domain and Range of Reciprocal

- x e R/ x cannot equal asymptote (0)

- y e R/ y cannot equal asymptote (0)

Finding x-intercepts

set y=0

- for reciprocal functions, set numerator to zero

Finding y-intercept

set x=0

Finding VA of reciprocal function

- set denominator to zero and factor to find zeros

Finding HA of reciprocal function

- if the degree of numerator is less than the degree of the denominator, the HA: y=0

- if the degree of the of the numerator is equal to degree of denominator, take the ratio of the leading coefficients

Oblique Asymptotes

- happens when the degree of the numerator is greater than the denominator by exactly 1

- use division to divide the numerator and denominator

- the answer is the equation of the oblique asymptote

- find the VA through the zeros of the denom.

Hole

when there is a common factor in the numerator and denominator of a reciprocal function

Cases when a rational function will not have a VA

1. If the denominator is unfactorable

2. if there is a hole

Reciprocal of quadratic

- vertex shares the same x-coordinate as original but y-coordinate is 1/y

- range is y>0 and y≥ 1/y

- domain is x e R, not including asymptotes

- if there is a vertical shift and it is not factorable (x^2+4), there are no VAs

End behaviour of reciprocal function CITATION

1. take two numbers close to the VA from the left and right side

2. this will determine how the function looks

HOW TO CITE:

ex. VA: X=2

as x --> 2⁻, f(x) --> negative infinity

as x --> 2⁺, f(x) --> positive infinity

Solving rational equations

- STATE RESTRICTIONS FIRST THING

- multiply both sides by LCD

- move to one side

- solve for variable

How long did it take to complete the puzzle question

- create the reciprocals of every given info: the first and second person and the total amount

- find LCD

- solve for x

Tshirt question

- state the original price of shirt

- state selling price of the shirt

- subtract og price with selling price and equate with profit

- use LCD to solve

- x value is number of shirts

- original price can be put into the first equation

Solving Rational Inequalities

- set restrictions

- move everything to one side

- find x-ints and VAs

- plot x-ints with closed circle on the number line

-plot VAs with open circle on the number line

- find test values in between to determine behaviour of function

- state solution

Arc Length Formula

theta = arc length/ radius

Convert Radians to degrees

x 180/pi

Convert degrees to radians

x pi/180

Angular velocity

= angle/time

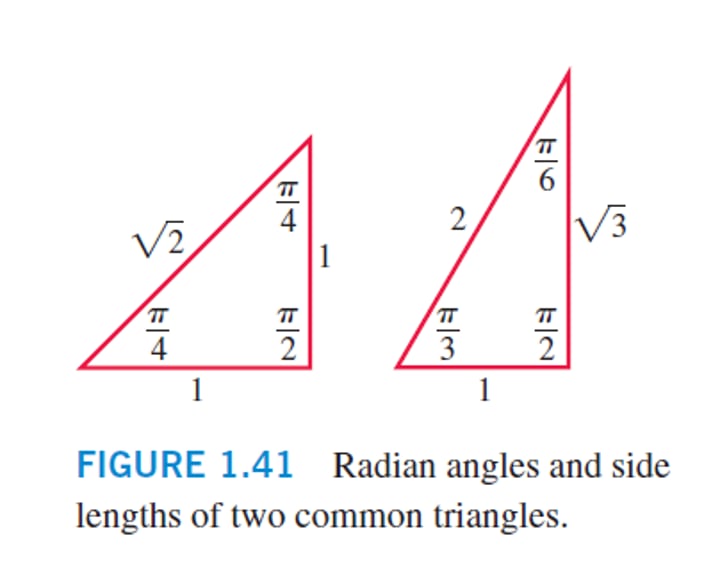
Special triangles

Determining equation of sinusoidal function

1. a=(max-min)/2

2. c=(max+min)/2 EQUATION OF AXIS

3. k= use 2pi/k to find period

Reciprocals of trig function

- asymptotes at x ints

- reflects on the max/min point

- domain is x e R, excluding n(pi) --> no asymptotes

Product Law

logb xy = logb x + logb y

Quotient Law

logb (x/y) = logb x -logb y

Power Law

logb x^n = nlogb x

To find different versions of an equation

Rewrite it using log laws

Half-Life Formula

A=Ao(1/2)^(t/h)

Combining Functions

Multiplying/dividing two even/odd functions results in an even functions

however the combo of odd/even creates and odd

Co-related acute angle

acute angle inline with the y-axis

Related acute angle

acute angle inline with x-axis