4.1 Linear and Angular Speed and Arc length and Sector area and converting radians to degrees

MOST IMPORTANT LINEAR AND ANGULAR SPEED FORMULA

V=Rω

Where:

• v = linear speed (m/s, cm/s, etc.)

• r= radius of circular path

• ω= angular speed (rad/s)

The linear speed is directly proportional to the radius. 

Tip: Larger radius → higher linear speed for same angular speed.

This allows you to change between speeds

Angular Speed

1⃣ Angular Speed (ω\omegaω)

• Measures how fast an object rotates.

• Formula:

ω=θ/t

Where

• ω = angular speed (radians per second, rad/s)

• θ = angle swept (radians)

• t = time

Units: rad/s or sometimes revolutions per minute (rpm).

Linear Speed

2⃣ Linear Speed (v)

• Measures how fast a point moves along a circular path.

• Formula: d/T

Where:

• d= diameter (m, cm, etc.)

• T = time (period-time for a complete trip)

Arc Length (S)

3⃣ Arc Length (s)

• Measures the distance along the circle subtended by an angle.

• Formula:

s=rθ

Where:

• s = arc length

• r = radius

• θ = angle in radians

Tip: Always convert degrees to radians if necessary:

Sector area

• Area of a slice of a circle corresponding to an angle θ\thetaθ.

• Formula:

A=1/2r²θ

Where:

• A = sector area

• r= radius

• θ = angle in radians

Tip: Degrees → radians conversion needed if angle is in degrees.

Converting radians to degrees and degrees to radians

Q: Formula to convert degrees → radians
A: radians=degrees×π/180

Q: Formula to convert radians → degrees
A: degrees=radians×180/π

Q: Relationship between radians and degrees
A: π radians=180∘

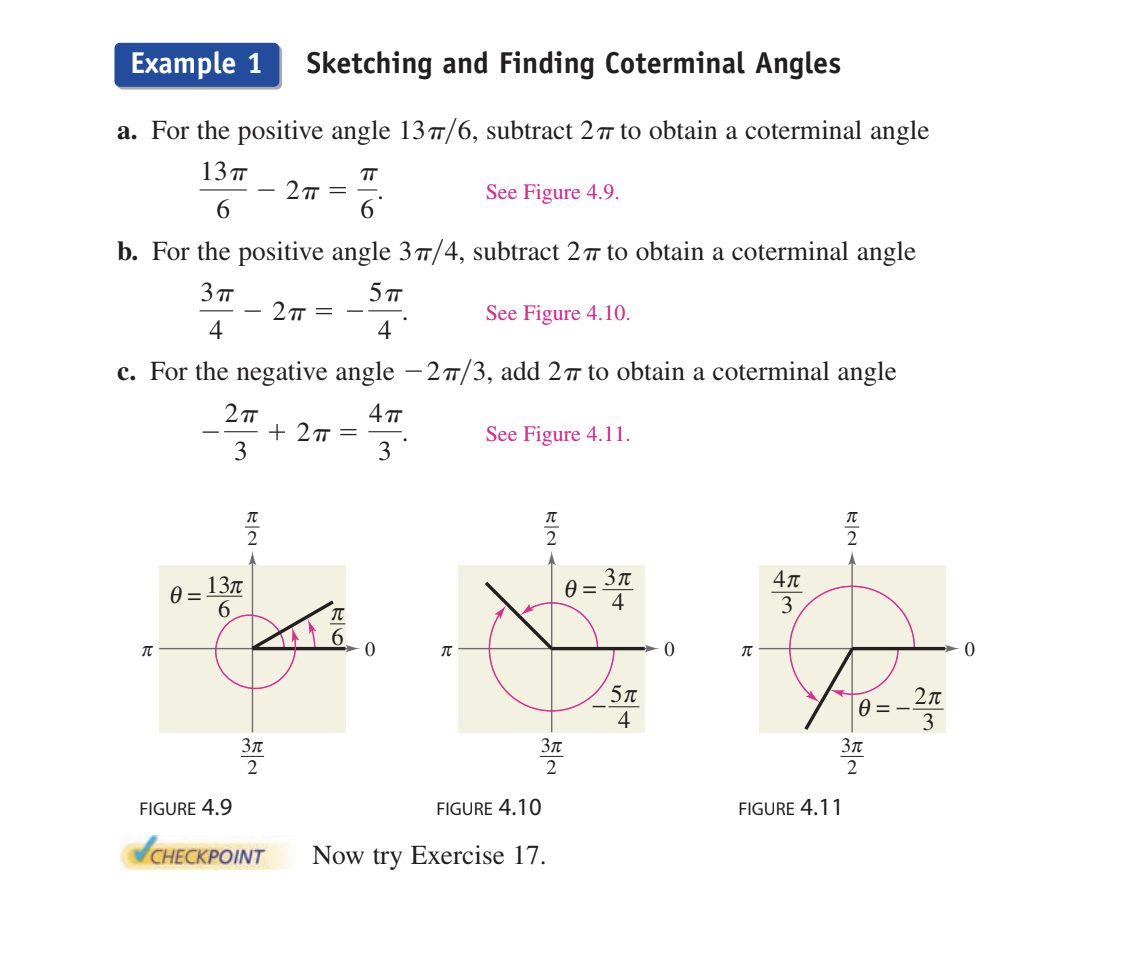
Example 1 Sketching and Finding Coterminal Angles

Example 2 Complementary and Supplementary Angles

Example 3 and 4 Converting from Degrees to Radians and Converting from Radians to Degrees

Example 5 finding Arc length

Example 6 and 7 finding Linear speed and finding linear and angular speed

Example 8 Area of a sector of a circle

HW part 1

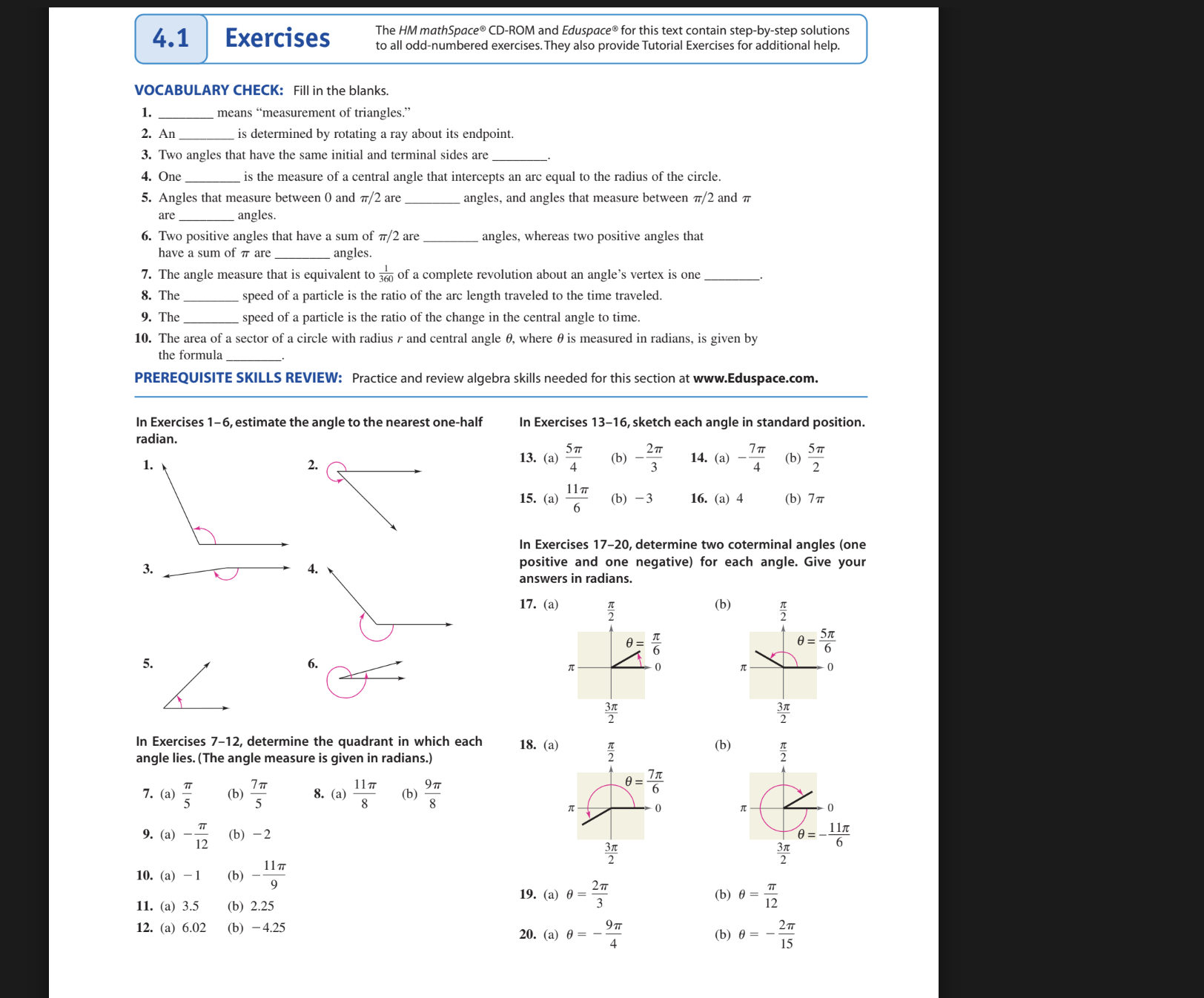
HW part 2

HW part 3