The Arrhenius Equation

What is the Arrhenius equation?

• An equation that shows how the rate constant (k) varies with temperature (T) and activation energy (Ea).

  k = Ae⁻ᴱᵃ/ᴿᵀ

Define the terms in the Arrhenius equation: k = Ae⁻ᴱᵃ/ᴿᵀ

• k = Rate constant

• A = Arrhenius constant (pre-exponential factor)

• Ea = Activation energy (in J mol⁻¹)

• R = Gas constant (8.31 J K⁻¹ mol⁻¹)

• T = Temperature (in Kelvin, K)

What is the logarithmic (straight line) form of the Arrhenius equation?

ln k = -Ea/RT + ln A

This matches the equation for a straight line, y = mx + c:

• y = ln k

• x = 1/T

• m (gradient) = -Ea/R

• c (y-intercept) = ln A

What are the two crucial unit conversions to remember when using the Arrhenius equation?

1. emperature (T): Must be in Kelvin (K). To convert: K = °C + 273

2. Activation Energy (Ea): Must be in Joules per mole (J mol⁻¹), not kJ mol⁻¹. To convert: J = kJ × 1000

State the logarithmic form of the Arrhenius equation. Identify the variables that would be plotted on the y-axis and x-axis to produce a straight-line graph.

• Equation: ln k = -Ea/RT + ln A [1]

• y-axis: ln k [1]

• x-axis: 1/T [1]

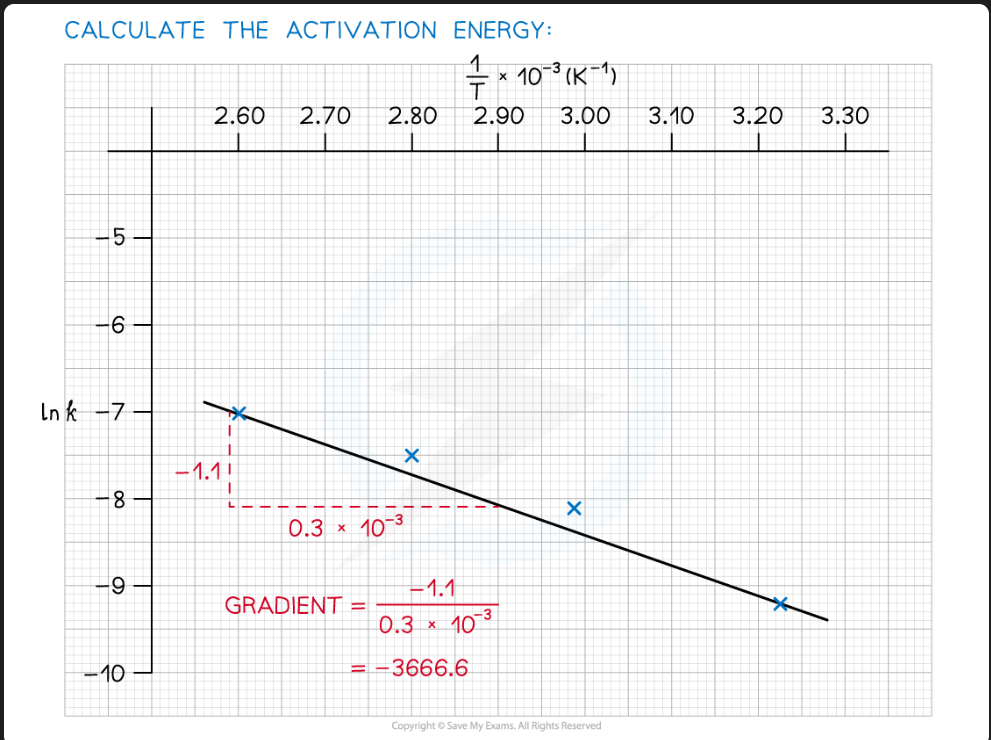
A student plots a graph of ln k against 1/T for a reaction. The gradient of the line of best fit is -6200 K.

Calculate the activation energy (Ea) for this reaction in kJ mol⁻¹. (The gas constant, R = 8.31 J K⁻¹ mol⁻¹) (3 marks)

• Formula: Gradient = -Ea / R So, Ea = -Gradient × R [1]

• Calculation (in J mol⁻¹): Ea = -(-6200) × 8.31 Ea = 51502 J mol⁻¹ [1]

• Conversion (in kJ mol⁻¹): Ea = 51502 / 1000 Ea = 51.5 kJ mol⁻¹ (to 3 s.f.) [1]

A catalyst is added to a reaction. Explain, in terms of the Arrhenius equation, how this leads to an increase in the value of the rate constant, k. (2 marks)

• A catalyst provides an alternative reaction pathway with a lower activation energy (Ea) [1].

• In the Arrhenius equation (k = Ae⁻ᴱᵃ/ᴿᵀ), a smaller value for Ea makes the exponential term (-Ea/RT) less negative, which increases the value of k

Calculate the activation energy of a reaction which takes place at 400 K, where the rate constant of the reaction is 6.25 x 10^-4 s^-1.

A = 4.6 x 10¹³ and R = 8.31 J K^-1 mol^-1.

How do you find the activation energy (Ea) experimentally using the Arrhenius equation?

• Measure the rate constant (k) at several different temperatures (T).

• Calculate ln k and 1/T for each data point (remembering to use T in Kelvin).

• Plot a graph of ln k (y-axis) against 1/T (x-axis).

• Draw a line of best fit (which will be a straight line).

• Measure the gradient (m) of this line.