01 - Biostatistics

biostatistics

application of statistical principles in medicine, public health, or biology

• collect information data → summarize, analyze, and interpret results

• make inferences

• draw conclusions

study samples

subsets of population of interest

• proportion (%) of adults in sample estimates proportion in population

• sample → inference → population

epidemiology

study of distribution and determinants of health events in population

• distribution = frequency and pattern

• determinants = cause and risk factors

clinical epidemiology

branch of epidemiology to apply epidemiologic methods to individual patient care

• purpose → determine impact of disease and health conditions in clinical settings to enhance patient care through evidence-based practice

• population-based approach → uses data from groups of patients to guide clinical decisions for individual patients

• risk assessment → evaluates likelihood of disease occurrence or outcomes in patient populations

• diagnostic accuracy → studies performance of diagnostic tests and procedures

• prognosis → predicts likely course and outcomes of disease

• treatment efficacy → assesses benefits and risks of therapeutic interventions

public health

health of population and all factors that influence health of individuals and groups of people

• improve health → education, inequalities, housing, lifestyle

• improve services → clinical effectiveness, planning

• protect health → infectious disease, environment

descriptive statistics

• data distribution

• data representation

measurements of central tendencies

• mean → average value; used for normal data

• median → middle value; used for skewed data

• mode → most frequent value; used for categorical data

measures of variability

• range → difference between highest and lowest values

• standard deviation → spread around the mean

• interquartile range → middle 50% of data set

data distribution

• normal distribution:

  • mean = median = mode

  • mean ± standard deviation

• skewed distribution:

  • mean affected by outliers

  • median ± interquartile range

data presentation

• box plot → median, IQR, outliers

• bar graph → compare groups (often ± SD)

• pie chart → proportions of categorical data

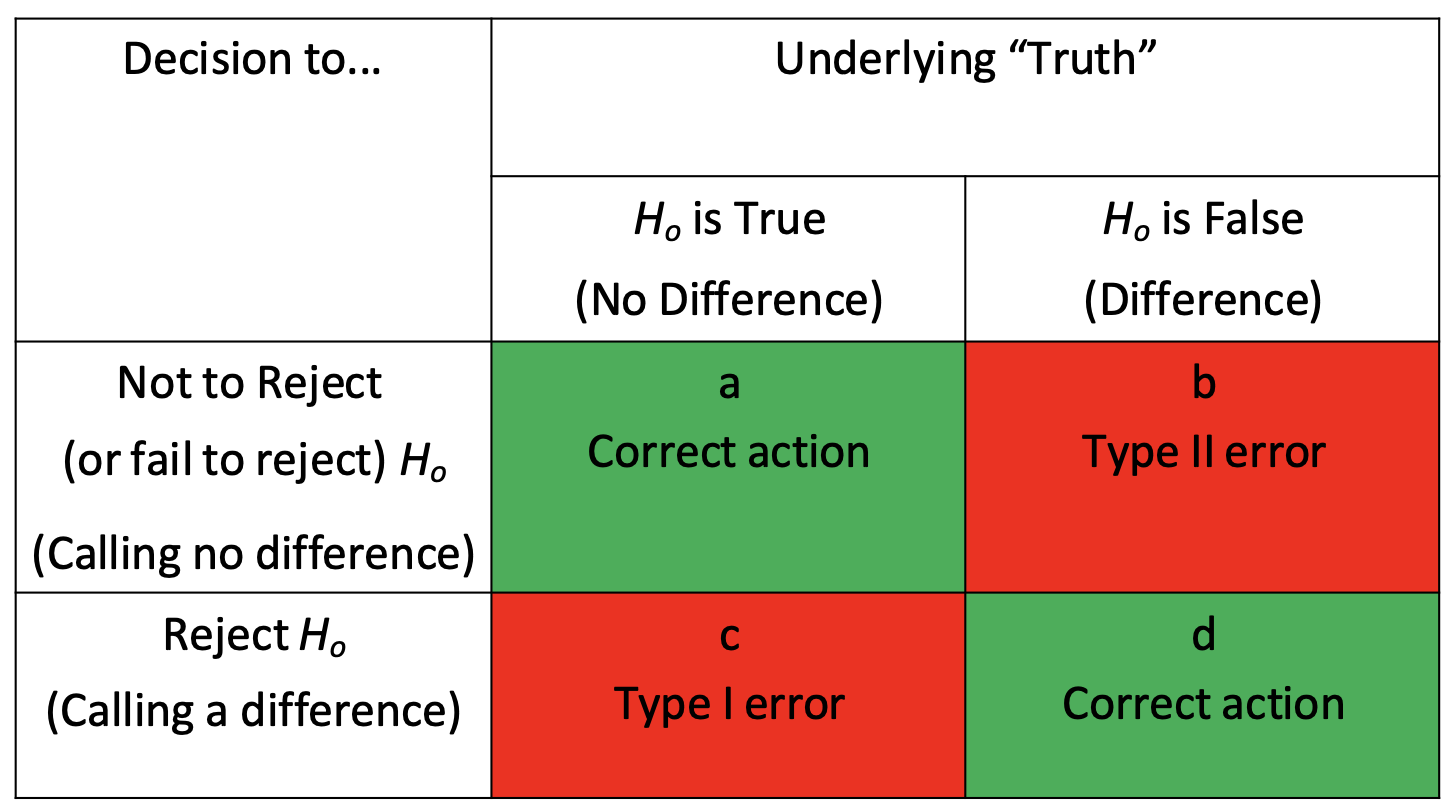
null and alternative hypothesis

• null (H₀):

  • no statistically significant difference

  • drug efficacy = placebo efficacy

  • researchers try to disprove/reject null hypothesis

• alternative hypothesis (H_a):

  • statistically significant difference

  • drug efficacy ≠ placebo efficacy

  • researchers try to prove

type I vs type II error

• type I (alpha) error → false positive; saying drug works when it doesn’t

• type II (beta) error → false negative; missing a real effect

hypothesis testing

tells about possibility of a chance influencing the results

• does not test for or tell anything about the possibility of a bias

• methods → compare p-values or evaluate confidence intervals

alpha level and p-value

• alpha level → level chosen before the study as maximum permissible error in study

  • usually 0.05

  • threshold used for rejecting null hypothesis

• p-value → probability that results occurred by chance if H_a is true

  • p < 0.05 → null hypothesis is rejected; there is statistically significant difference between groups

  • p ≥ 0.05 → study has failed to reject null; no statistically significant difference

confidence intervals

range where true value likely lies

• gives idea of accuracy of point estimates

• assess statistical significance, using null value as reference

• CI = 1 - alpha; if alpha = 0.05 → 95% CI

  • narrow CI = high precision; wide CI = low precision

  • bigger sample → narrower CI

• difference in means for 95% CI = difference ± 1.96 × standard error

• standard error = SD / √n

process of determining whether something is statistically significant

1. state a null hypothesis, H₀

2. choose an alpha level

3. review p-value from statistical model (analysis report) and compare with alpha

4. review confidence level from statistical model → 1 for ratios, 0 for difference

5. determine statistical significance → p-value and CI should give same conclusion

difference vs ratio measures

• difference measure → how much higher/lower?; null = 0

  • calculates absolute change by subtracting → group A - group B

  • measures mean difference, risk difference, difference in proportion

  • null = 0 → difference of 0 = no difference between groups

  • ex: treatment group mean BP = 130; control group mean BP = 135

    • difference = 130 - 135 = -5

    • 95% CI = (-10, +2)

    • includes 0 in CI → not statistically significant

• ratio measures → how many times higher/lower?; null = 1

  • compares group using division → group A / group B

  • measures relative risk, odds ratio, hazard ratio

  • null = 1 → same risk in both groups

  • ex: treatment group risk = 10%; control group risk = 20%

    • relative risk = 0.10 / 0.20 = 0.5

    • 95% CI = (0.3, 0.9)

    • does not include 1 → statistically significant

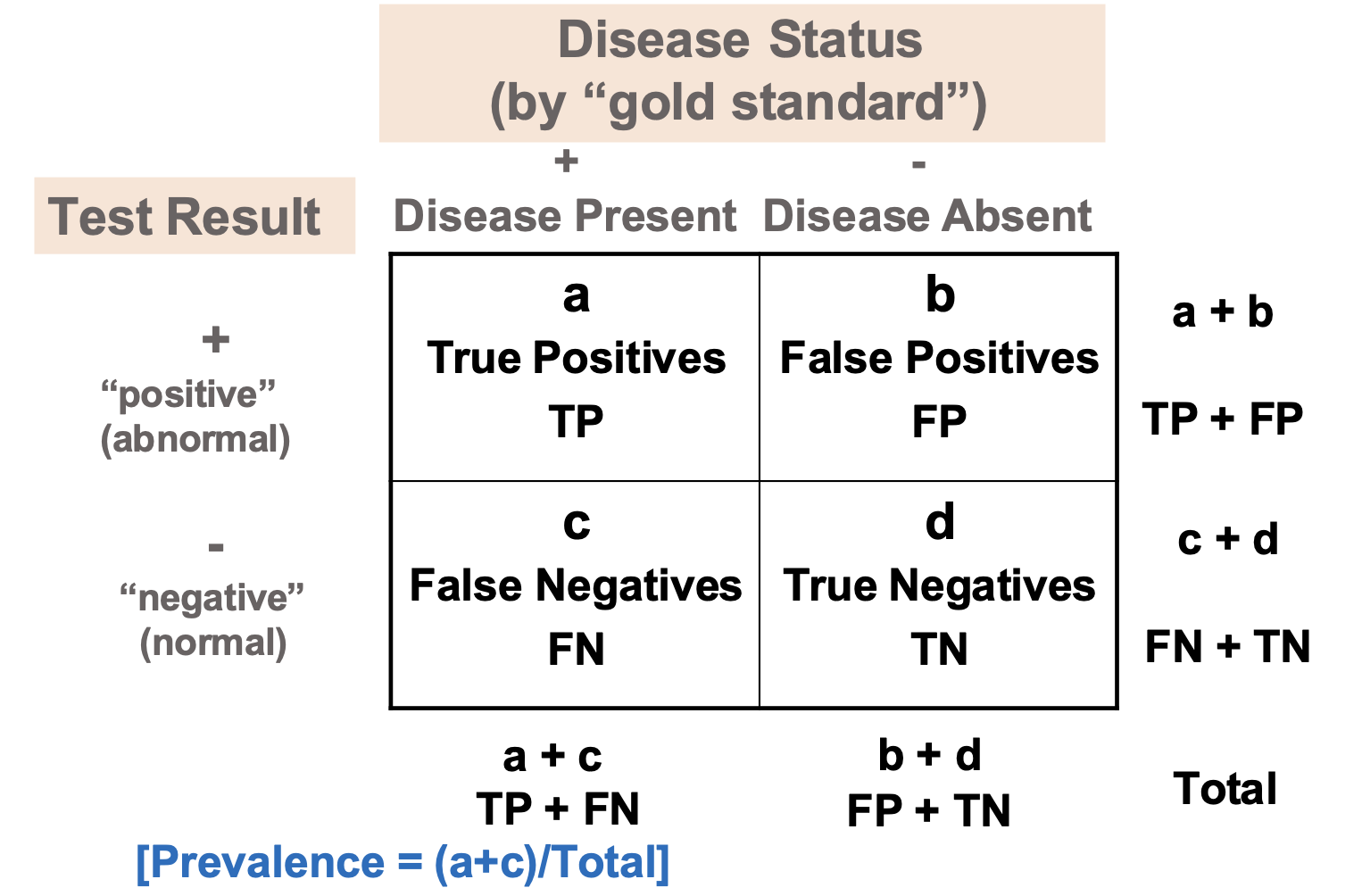
test performance measures

• sensitivity → TP / (TP + FN)

  • among persons with disease, percent who have positive tes

• specificity → TN / (FP + TN)

  • among persons without disease, percent who have negative test

• positive predictive value (PPV) → TP / (TP + FP)

  • among persons with positive test, percent who have disease

• negative predictive value (NPV) → TN / (FN + TN)

  • among persons with negative test, percent who do not have disease

likelihood ratios (LR)

measures diagnostic accuracy in evaluating particular disease or condition

• when a patient tests positive:

  • LR+ = sensitivity / 1-specificity = true positive rate / false positive rate

  • LR+ → rule in disease (>1)

• when a patient tests negative:

  • LR- = 1-sensitivity / specificity = false negative rate / true negative rate

  • LR- → rule out disease (<1)

statistical and clinical significance

statistical significance does not mean that results are clinically important

• statistical significance → is result real or chance?

• clinical significance → does it matter to patients?

• factors → sample size, duration, cost, ease of implementation

bias

interference tending to produce results that depart systematically from true values

• selection bias → groups differ at baseline

• measurement bias → inaccurate measurement

• confounding bias → third variable distorts effect

internal vs external validities

• internal validity → results are correct for sample

• external validity → results holds true in other settings

precision vs accuracy

• precision (reliability) → reproducibility

• accuracy (validity) → closeness to truth

sample size considerations

larger sample → higher power → less chance error

• significance → alpha value = 0.05

• power → ≥ 80%

• effect size → meaningful definition of “different”

correlation

measures linear relationship only

• r = -1 or 1 only

• increasing correlation when r is closer to 1

• correlation ≠ causation

discrete vs continuous data

• discrete → can only assume limited number of values within given range

  • nominal = categories (yes/no)

  • ordinal = ranked (class I-IV)

• continuous → can take on any value within given range

  • interval = no true zero (ºF)

  • ratio → true zero (BP, HR)

probability rules

• P(developing disease) = probability of developing disease

• P(A) + P(not A) = 1 or 100%

• additive rule → mutually exclusive

• multiplicative rule → independent events

  • independence = P(A occurring) not related to P(B occurring)

• conditional probability → P(A|B) = P(A occurring) given P(B occurring)

descriptive vs inferential statistics

• descriptive → summarizes and describes data collected

  • may be done visually and numerically

• inferential → using population samples to make generalizations and infer/draw conclusions

  • methodology depends on data type and study design

  • statistical inference can be made by estimation or hypothesis testing

common stastical tests

• t-test → checks difference between means of two groups (continuous)

• ANOVA → checks difference between means of three or more groups (continuous)

• chi-square → checks difference between three or more proportions or percentages (categorical)

• Fisher’s exact test → checks difference between two proportions or percentages (categorical)