Corporate Finance Ch3

PV of bonds

annuity + discounted PV of final payment

C(1/r - 1/r(1+r)^t) + par/(1+r)^t

or if paid multiple times a year:

where y = yield to maturity (opportunity cost of capital)

n = number of payments each year

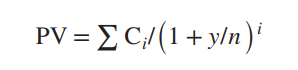
Yield to maturity

THE DISCOUNT RATE THAT EXPLAINS THE BOND PRICE. Opportunity cost of capital. doesnt equal the coupon interest rate; that only represents interest payments, not the difference btwn the par and price.

discount bond

a bond where the price is less than the face value. The yield to maturity exceeds the coupon rate

capital gain

premium bond

a bond that sells above par. yield to maturity < coupon rate

capital loss

par bond

price = par, yield = coupon rate

treasury bonds vs notes vs bills

bonds: 10+ years

notes: <10 years

bills: < 1 year

how are bond prices usually expressed

as a percentage of face value

Do prices and yields move inversely or directly? 

INVERSELY

rate of return

(coupon income + price change)/investment

Macaulay Duration

t = # of years until the ith payment

weighted average of the times to each of the cash pyaments. the PV of the cash flow received at that time / cash flow of the bond

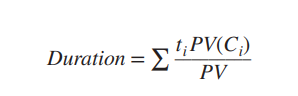
modified duration

duration / (1+yield)

measures the percentage change in bond price for a 1 percentage point change in yield

helpful to assess interest rate risk

term structure of interest rates

the relationship between long and short term interest rates

how to use the spot rate

the individual discount rate at a point in time. To find the yield to maturity, discount each cash flow by the SPECIFIC YEAR’S SPOT RATE and find that present value. Then, set the PV equal to equation using a uniform yield to maturity and solve for it.

stripped bonds/strips

bonds broken down into mini bonds that each pay 1 of the interest payments/principal

to calculate spot rate at a specific year:

Discount Factor at specific year = 1/(1+spot rate at specific year)^specific year                 set equal to known DF and solve for r

arbitrage

cases where two identical sets of future cash flows sell at different prices.

expectations theory in the bond market

expected returns of a series of short term bonds must return the same as a single long-maturity bond

are prices for short or long-term bondsmore sensitive?

long term

nominal dollars vs real dollars

nominal: the literal cash flow in dollars you will receive

real: discount future cash flow by rate of inflation to show its real purchasing power that you will receive

real cash flow at date t

nominal cash flow at date t / (1+inflation rate)^t

real rate of return

1+rreal = (1+rnominal)/(1+inflation rate)

indexed bonds

make cash payments linked to inflation. real cash flows are fixed instead of nominal cash flows. 

Fisher’s theory

a change in the expected inflation rate causes the same proportionate change in the nominal interest rate

own currency debt

if government issues bonds/borrows in its own currency, lower risk because they can just print money to payment

eurozone debt

own currency debt not applicable to EU countries that use euros, because they use the european central bank and do not print their own money.