Geometry Flash Cards v2

Module 1 to Module 20. 245 flash cards total. Some cards have been minimized to one card and have no images. The images will be resized so that it is easier to use the cards later.

1) Point

An undefined term in geometry, it names a location and has no size

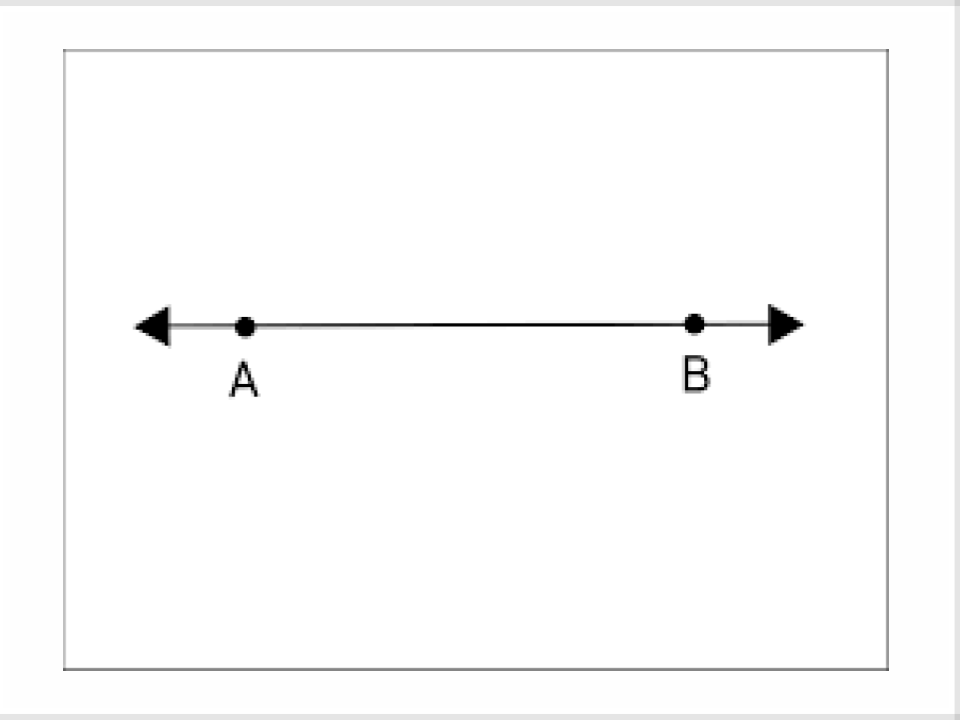
2) Line

An undefined term in geometry, a straight path that has no thickness and extends forever

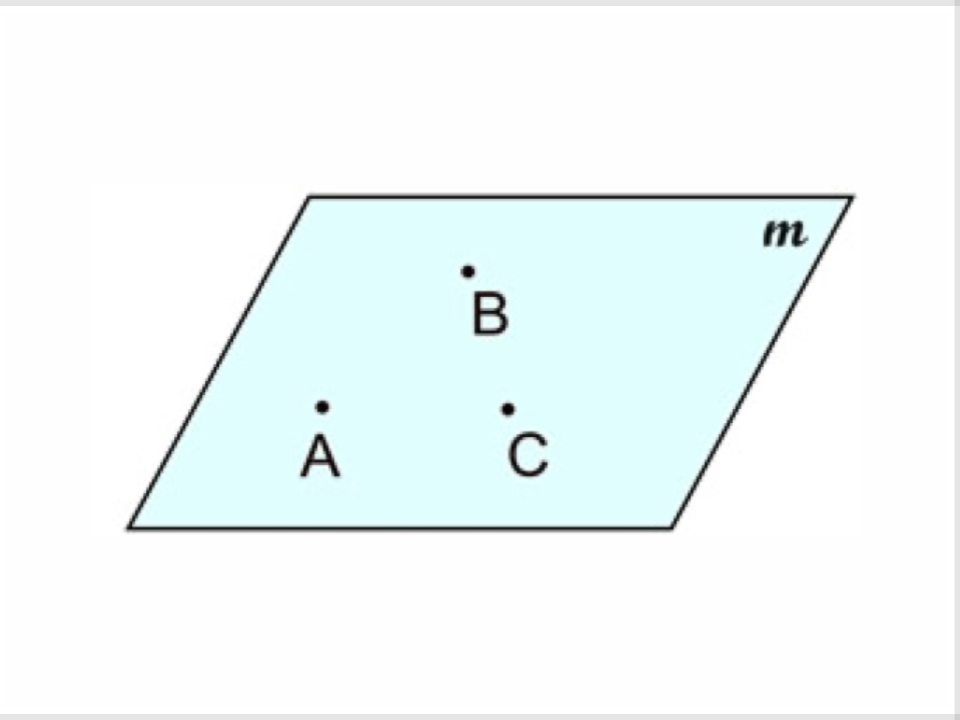
3) Plane

An undefined term in geometry, it is a flat surface that has no thickness and extends forever

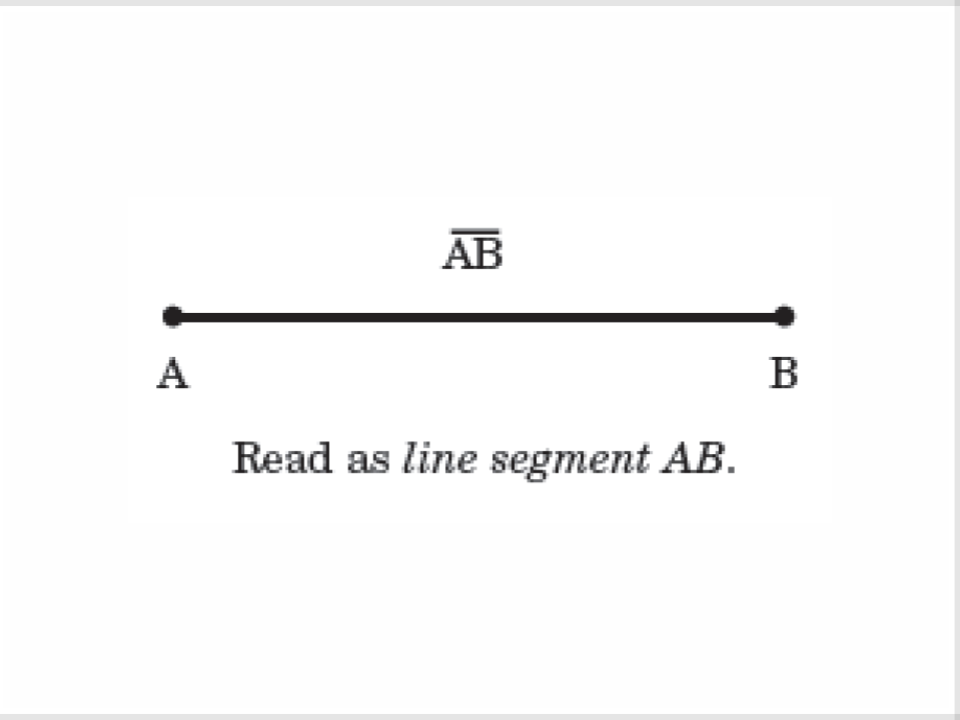
4) Segment of a Line

A part of a line consisting of two endpoints and all points between them

5) Endpoints

The point at an end of a segment or the starting point of a ray

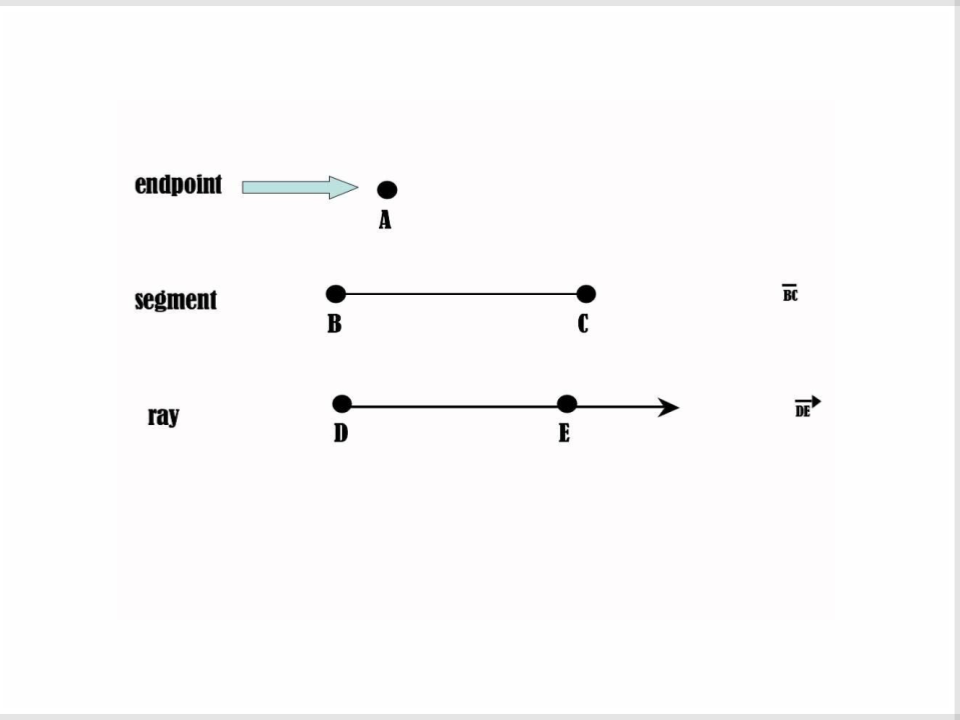
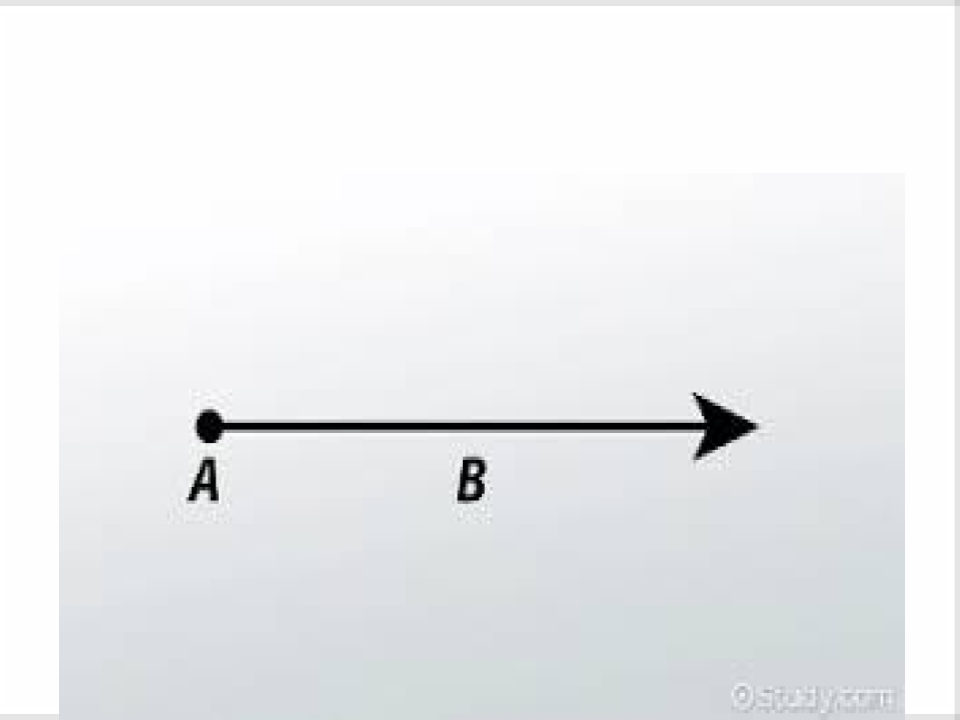
6) Ray

A part of a line that starts at an endpoint and extends forever in one direction

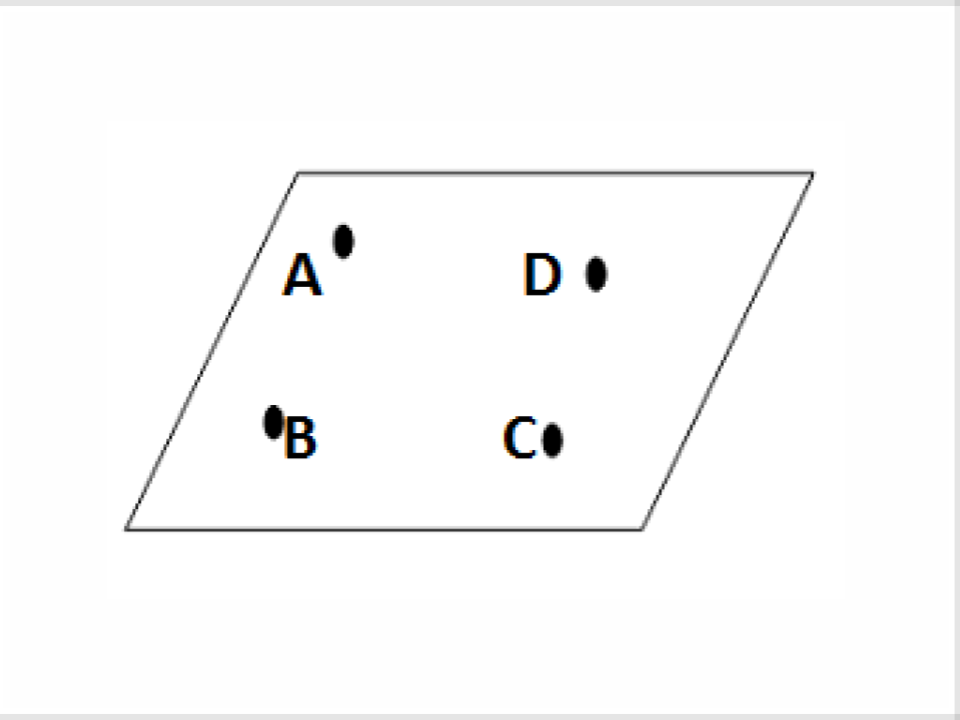
7) Coplanar

Points that lie on the same plane

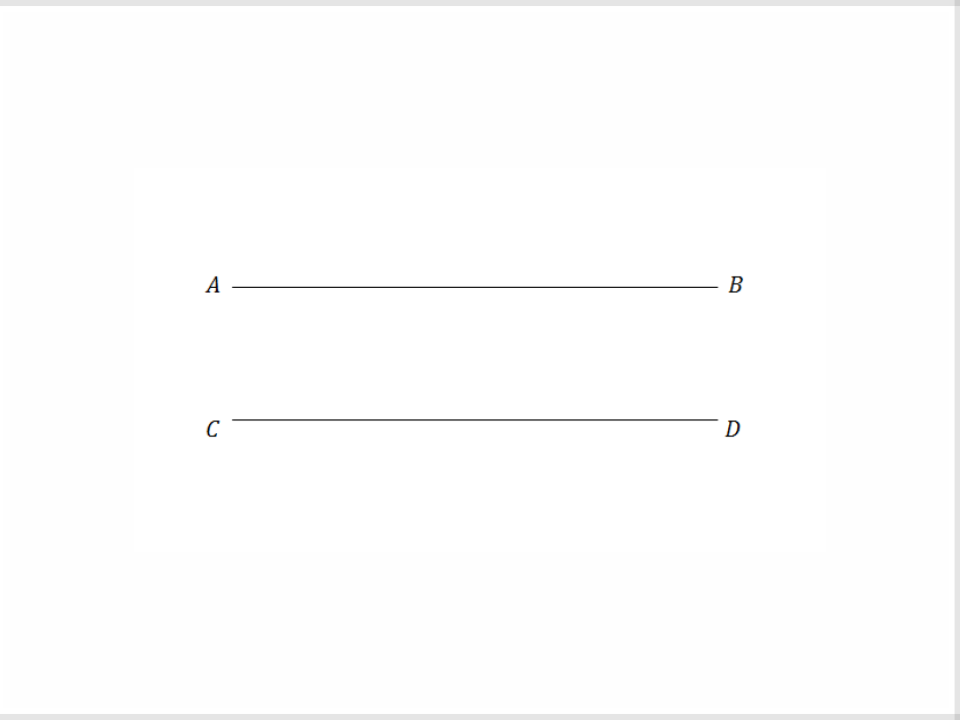
8) Parallel Lines

Lines in the same plane that do not intersect

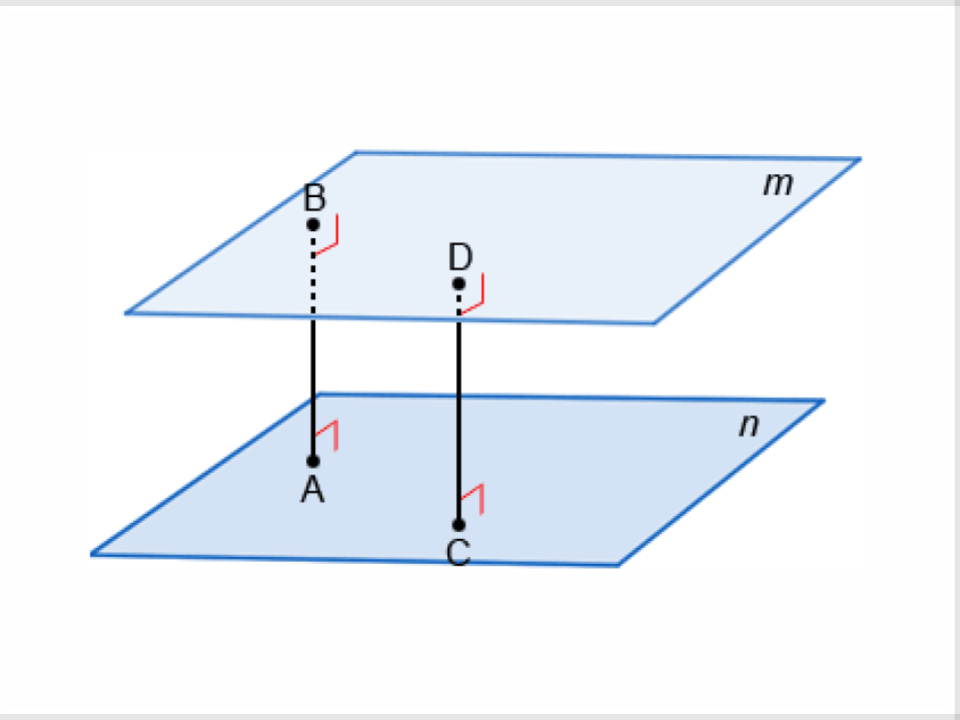
9) Parallel Planes

Planes that do not intersect

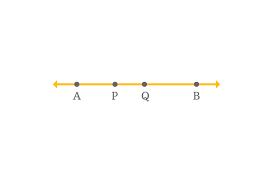
10) Collinear

Points that lie on the same line

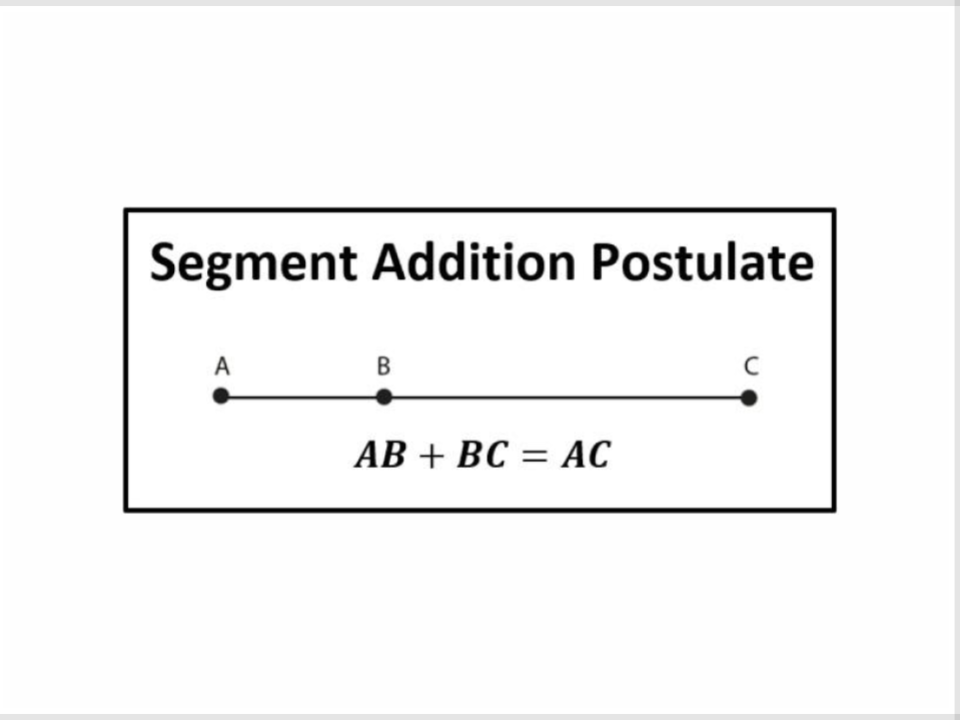
11) Segment Addition Postulate

A statement about collinear points

12) Postulate

A statement that is accepted as true without proof. Also called an axiom

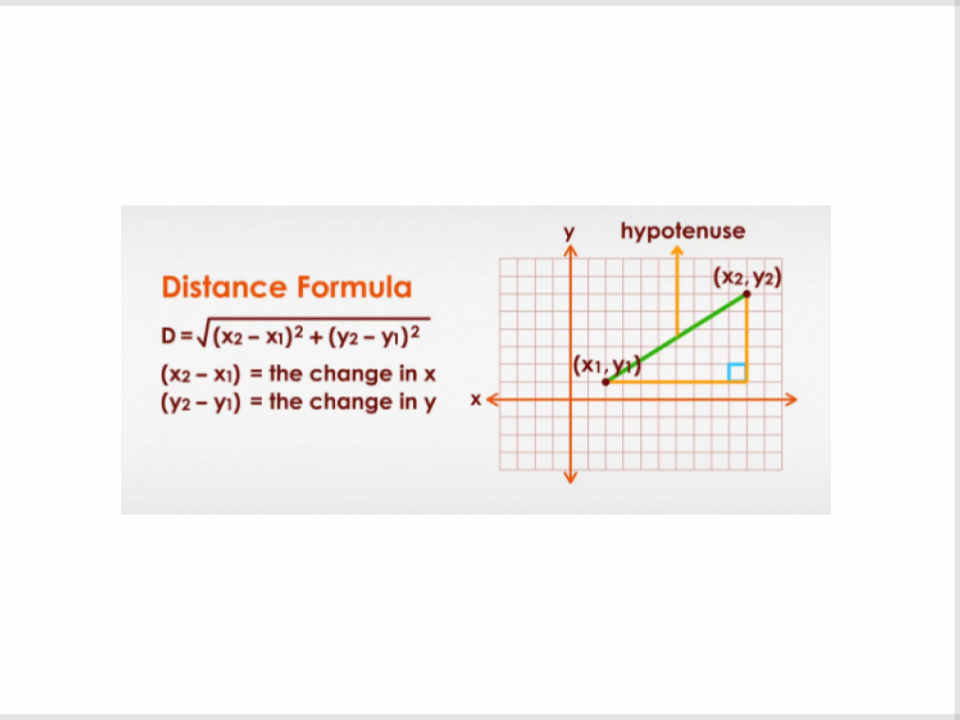
13. Distance Formula

The distance between two points (x1, y1) and (x2, y2) on the coordinate plane is √((x2-x1)^2 + (y2-y1)^2)

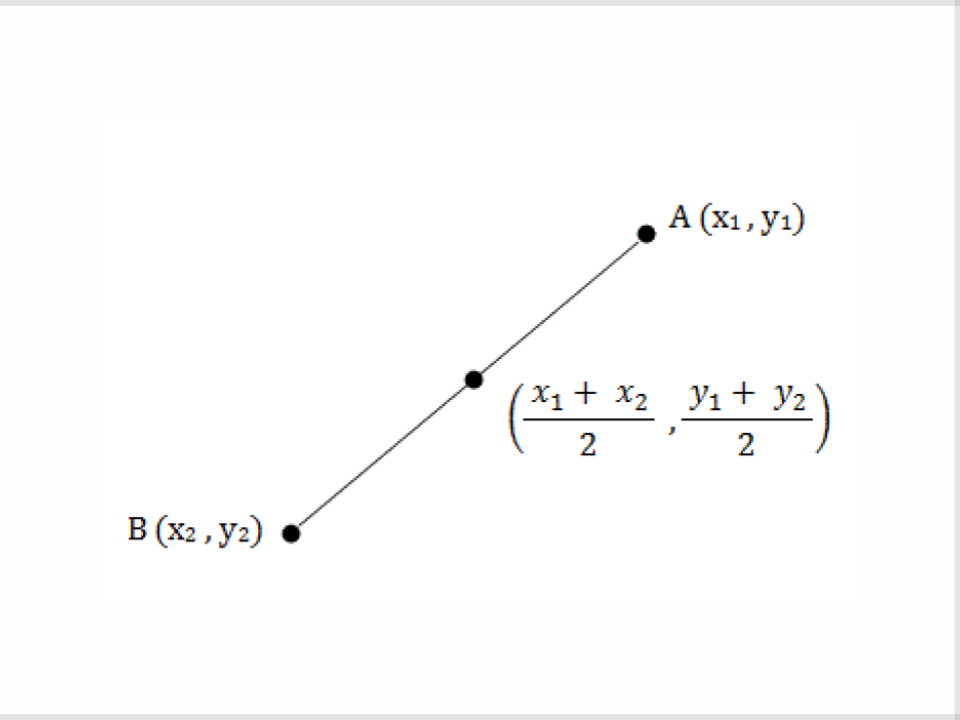
14) Midpoint

The point that divides a segment into two congruent segments

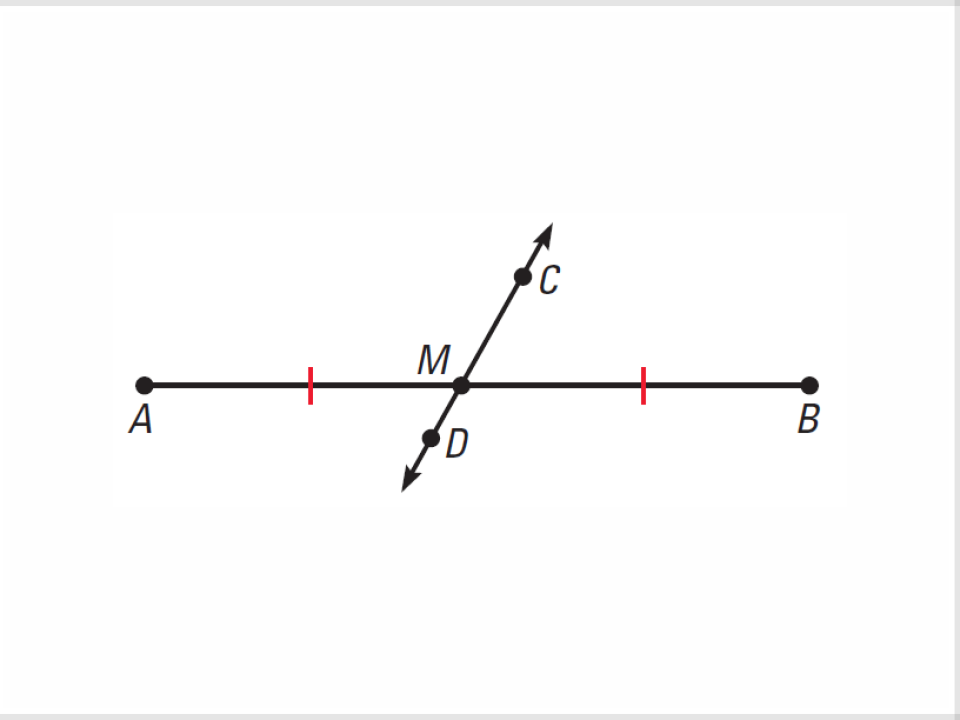
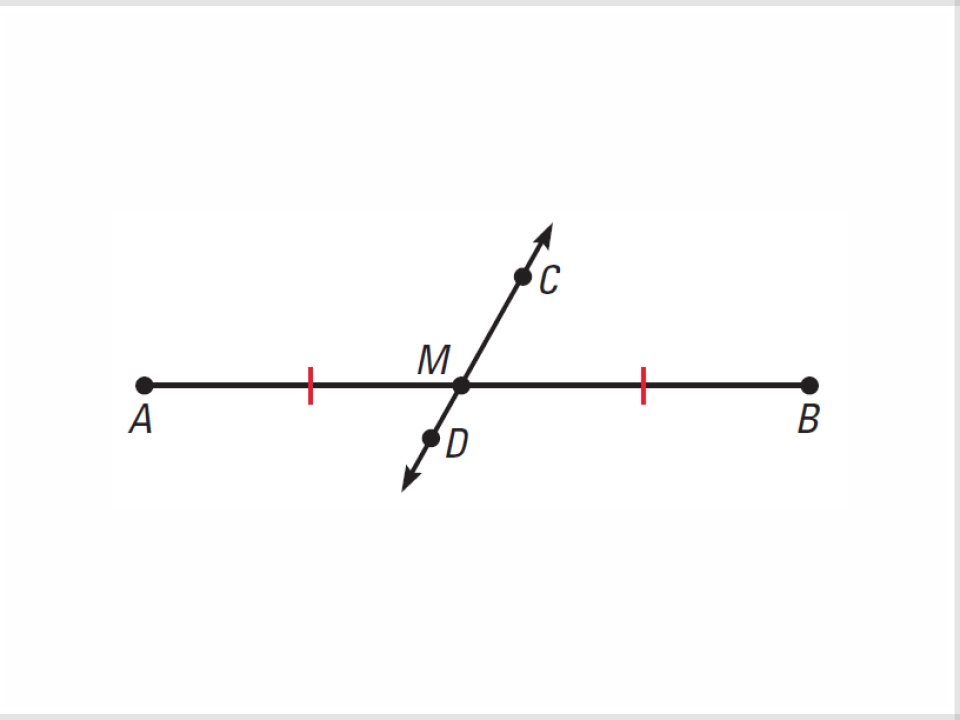
15) Segment Bisector

A line, ray, or segment that divides a segment into two congruent segments

16) Midpoint Formula

The midpoint M of segment AB with endpoints A(x1, y1) and B(x2,y2) is given by m( (x1+x2)/2, (y2+y1)/2 )

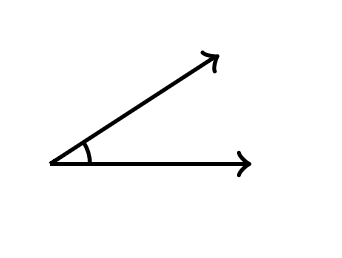
17) Angle

Figure formed by two rays with a common endpoint

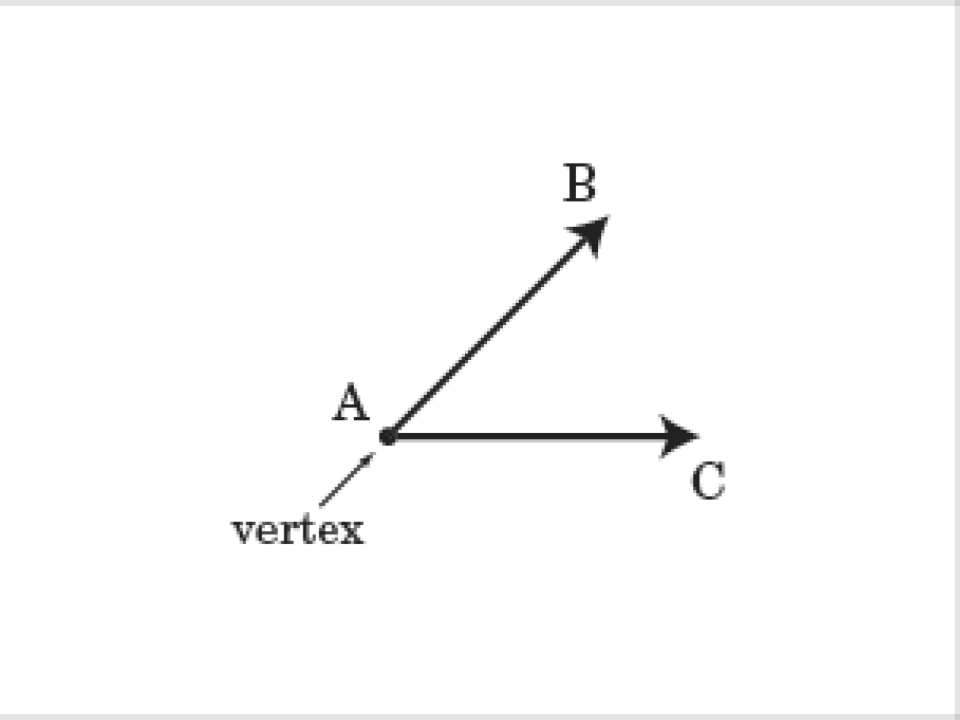
18) Vertex of an Angle

The common endpoint of the sides of the angle

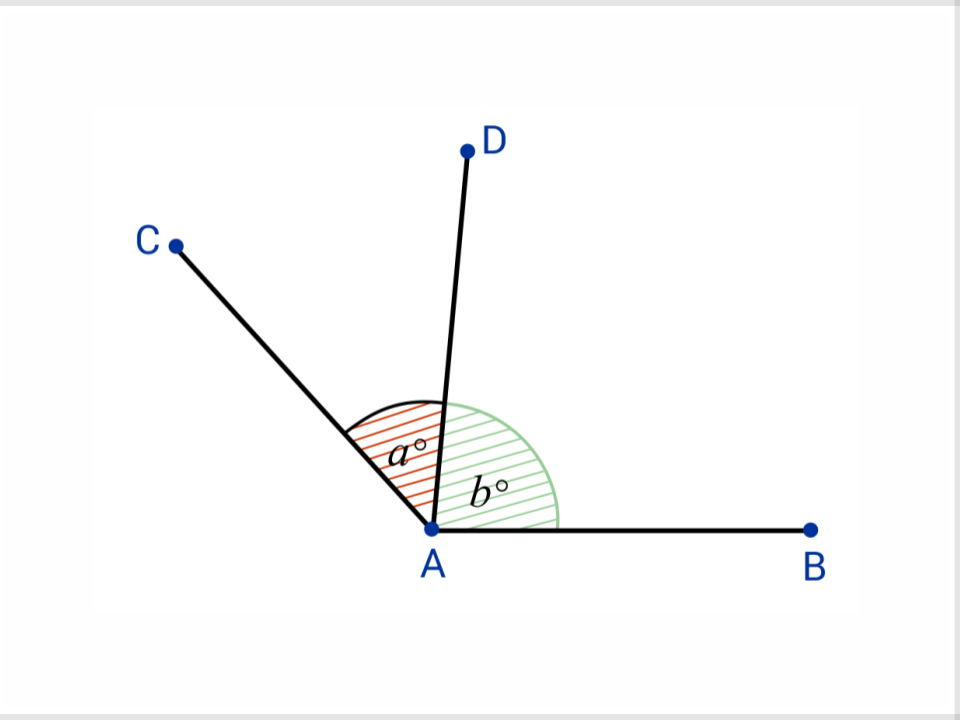
19) Adjacent Angles

Two angles in the same plane with a common vertex and a common side, but no common interior points

20) Side of an Angle

One of two the rays that form an angle

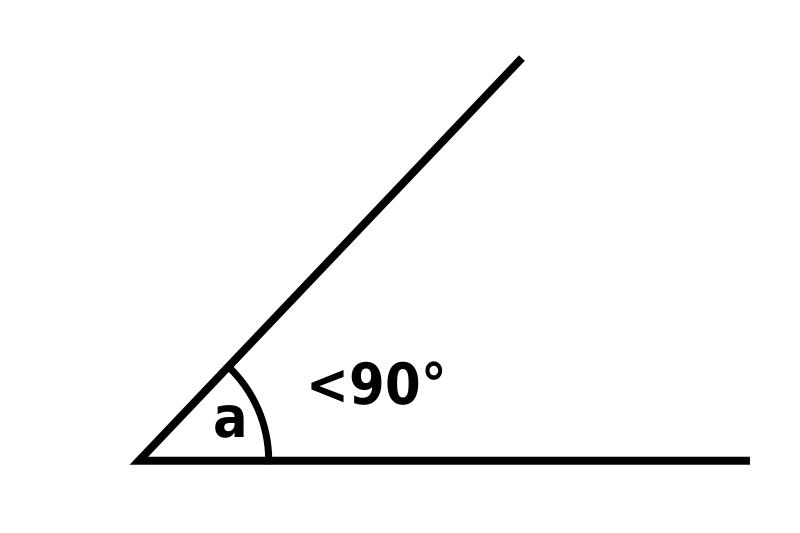
21) Acute Angle

An angle that measures greater than 0 degrees and less than 90 degrees

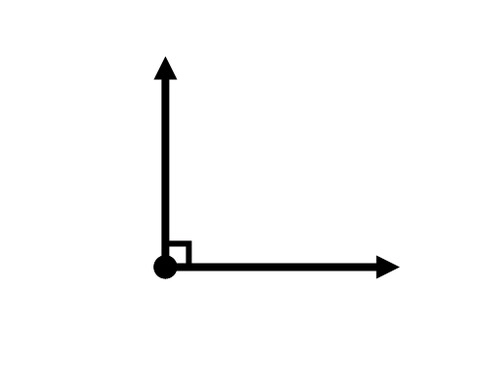
22) Right Angle

An angle that measures 90 degrees

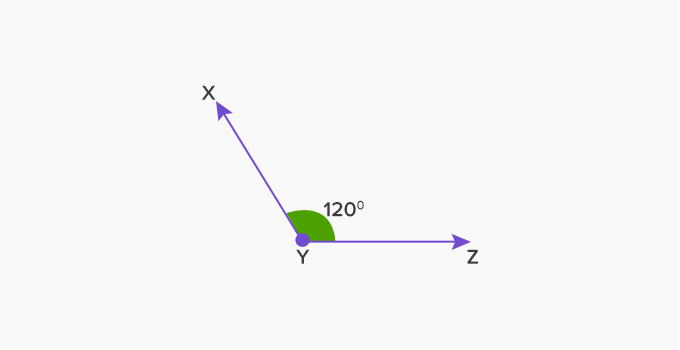
23) Obtuse Angle

An angle that measures greater than 90 degrees and less than 180 degrees

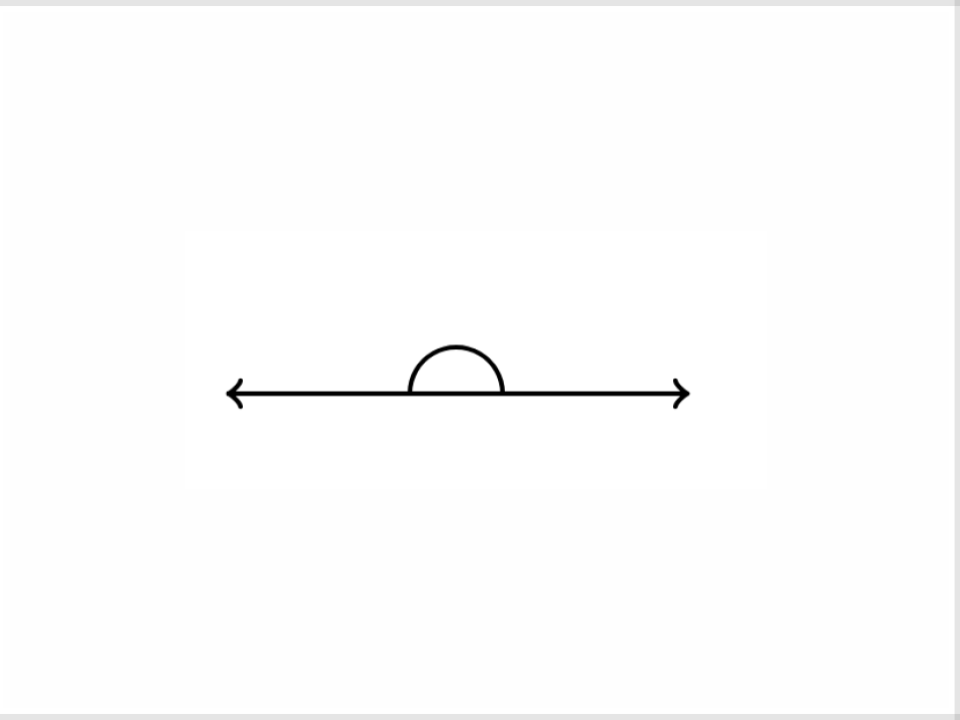
24) Straight Angle

A 180 degree angle

25) Degrees

A common measurement unit for circular arcs

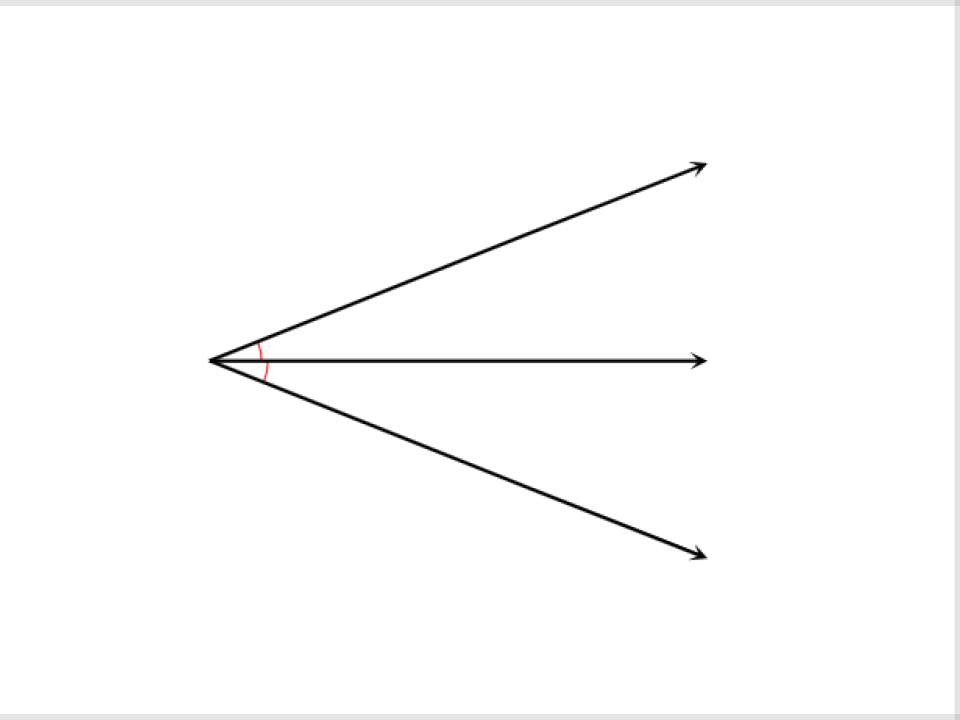
26) Angle Bisector

A ray that divides an angle into two congruent angles

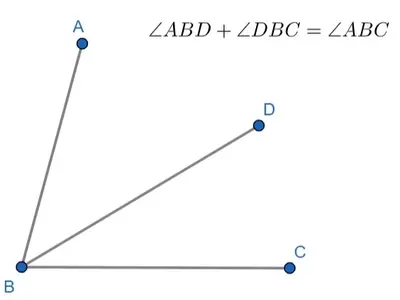
27. Angle Addition Postulate

A ray that divides an angle into two angles that both have the same measure

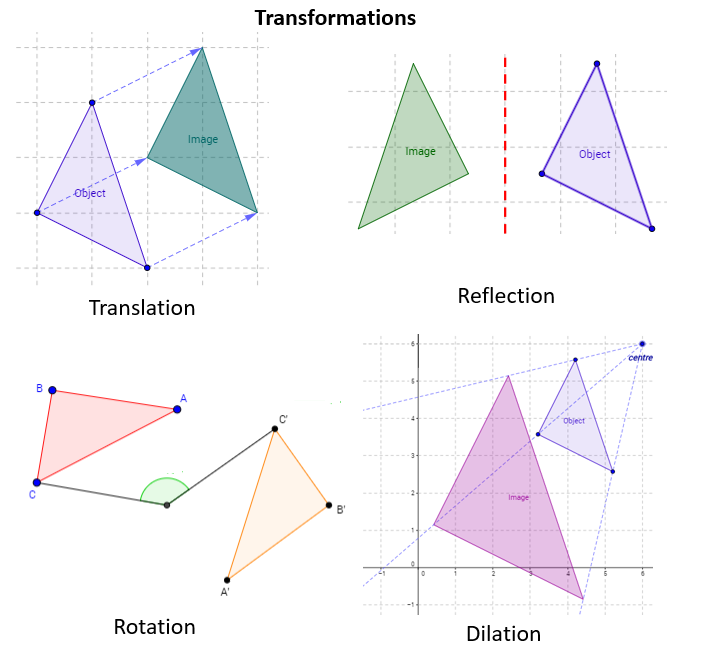
28) Transformation

A change in the position, size, or shape of a figure on a graph

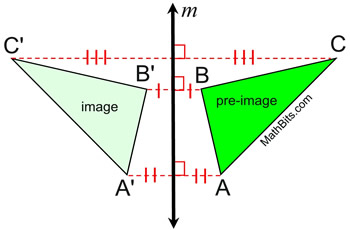
29) Preimage

The original image in a transformation

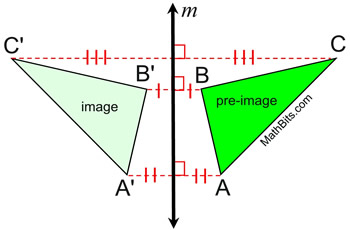
30) Image

The image that results from a transformation of a figure known as the preimage

31) Isometry

A transformation that does not change the shape or size of a figure. Examples: reflections, translations, and rotations

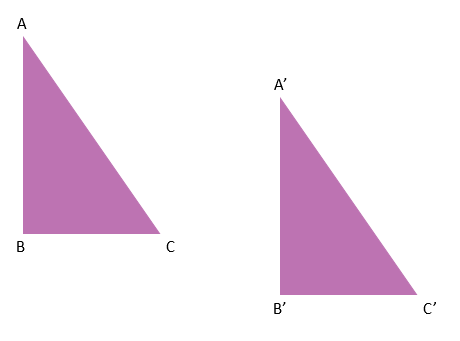
32) Properties of Rigid Motions

Transformations that changes the position of the a figure without changing size or shape

Rigid Motions preservers:

Distance

Angle Measure

Betweenness

Collinearity

Parallelism

33) Conjecture

A statement that is believed to be true

Example:

A sequence begins with the terms 2, 4, 6, 8, 10

A reasonable conjecture is that the next term in the sequence is 12

34) Inductive Reasoning

The process of reasoning that a rule or statement is true because specific cases are true

35) Deductive Reasoning

The process of using logic to draw conclusions

36) Theorem

A statement that has been proven

37) Counter Example

An example that proves that a conjecture or statement is false

38) Conditional Statement

A statement that can be written in form “if p, then q,” where p is the hypothesis and q is the conclusion

If x+1=5 (hypothesis), then x=4 (conclusion)

39) Additional Property of Equality

If a=b, then a+c = b+c

40) Subtraction Property of Equality

If a=b, then a-c = b-c

41) Multiplication Property of Equality

If a=b, then ac =bc

42) Division Property of Equality

If a=b, then a/c = b/c

43) Reflexive Property of Equality

If a=a, then a=a

44) Symmetric Property of Equality

If a=b, then b=a

45) Transitive Property of Equality

If a=b and b=c, then a=c

46) Substitution Property of Equality

If a=b, then b can be substituted for a in any expression

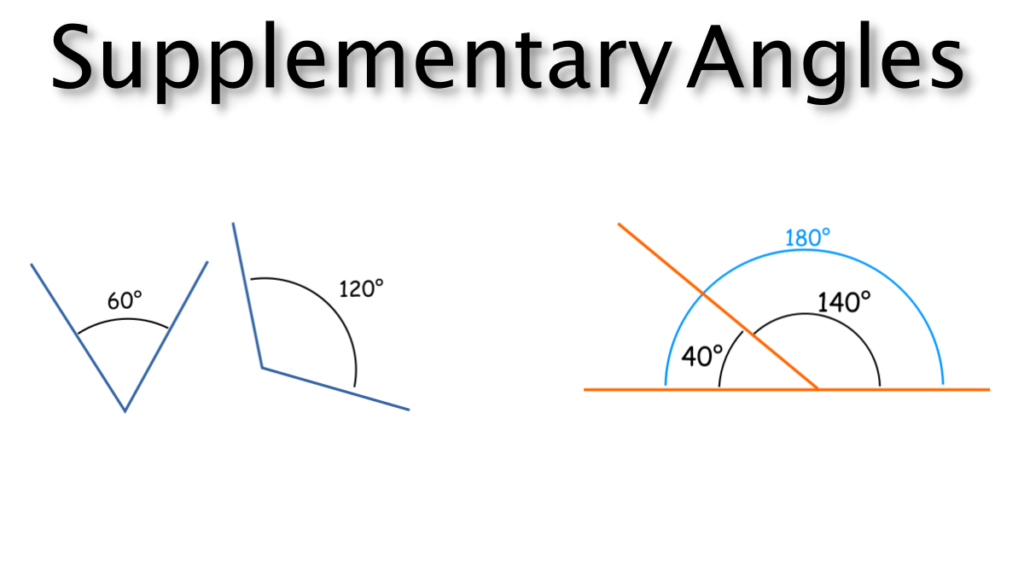
47) Supplementary Angles

Two angles whose measures have a sum of 180 degrees

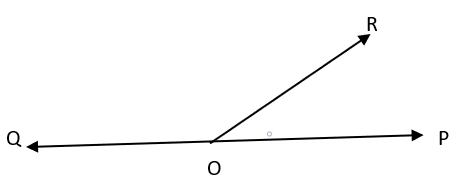
48) Linear Pair

A pair of adjacent angles whose non-common side is opposite rays

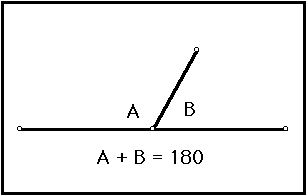
49) Linear Pair Theorem

If two angles form a linear pair, then they are supplementary

50) Postulates about Point, lines, and Planes

Through any two points, there is exactly one line

Through any three noncollinear points, there is exactly one plane containing them

If two points lie in a plane, then the line containing those points lie in the plane

If two lines intersect, then they intersect in exactly one time

If two planes intersect, then they intersect in exactly one line

51) Vector

A quantity that as both magnitude and direction

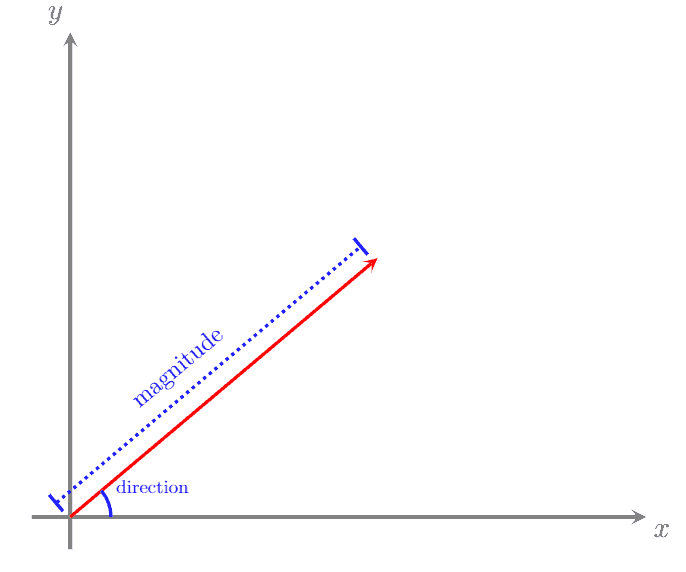
52) Initial point of Vector

The starting point of a vector

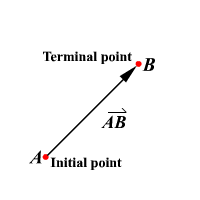
53) Terminal Point of Vector

The endpoint of a vector

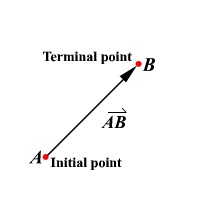
54) Translation

Transformation that shifts or slides every point of a figure or graph the same distance in the same direction

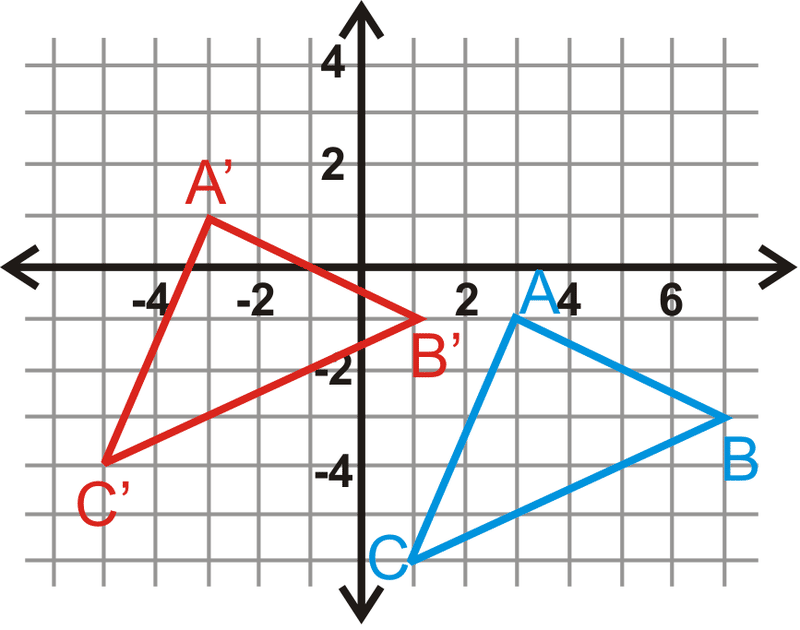
55) Rules of Translations

Translation Right:

(x,y)→(x+a,y)

Translation Left:

(x,y)→(x-a,y)

Translation Up:

(x,y)→(x,y+a)

Translation Down:

(x,y)→(x,y-a)

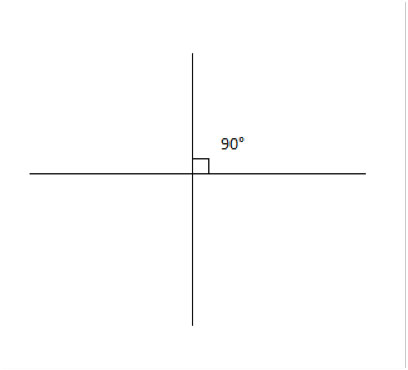
56) Perpendicular Lines

Lines that intersect at 90 degree angles

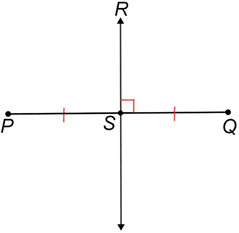
57) Perpendicular Bisector of a Segment

A line perpendicular to a segment at the segment’s midpoint

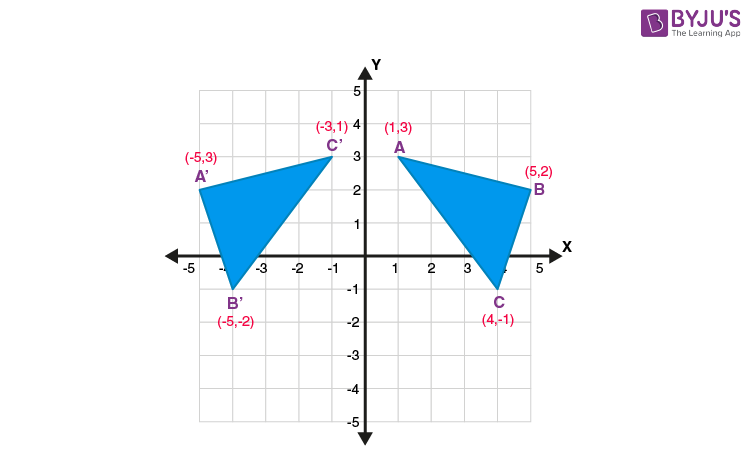
58) Reflection

A transformation across a line, called the line of reflection, such that the line of reflection is perpendicular bisector of each segment joining each point and its image

59) Rules of Reflection

Reflection across x-axis:

(x,y)→(x,-y)

Reflection across y-axis:

(x,y)→(-x,y)

Reflection across y=x:

(x,y)→(y,x)

Reflection across y=-x:

(x,y)→(-x,-y)

60) Rotation

A transformation about a point p, also known as the center of rotation, such that each point and its image are the same distance from p. All angles with vertex p formed by a point and its image are congruent

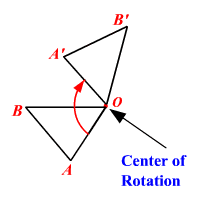
61) Center of rotation

The point around which the figure is rotated

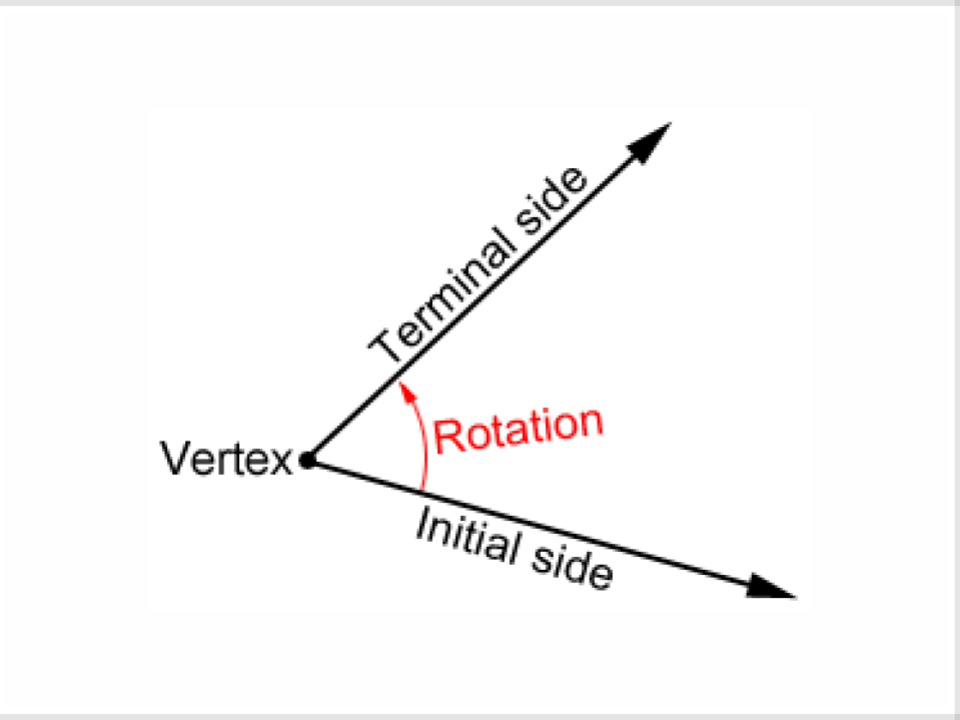
62) Angle of Rotation

An angle formed by a rotating ray, called the terminal side, and a stationary reference called the initial side

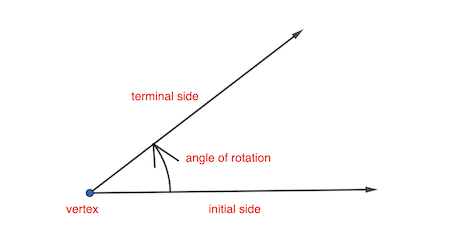
63) Rules of Rotations

90 degree rotation counterclockwise:

(x,y)→(-y,x)

180 degree rotation:

(x,y)→(-x,-y)

270 degree rotation counterclockwise:

(x,y)→(y,-x)

360 degree rotation:

(x,y)→(x,y)

64) Symmetry

In the transformation of a figure such that the image coincides with the preimage, the image and preimage have symmetry

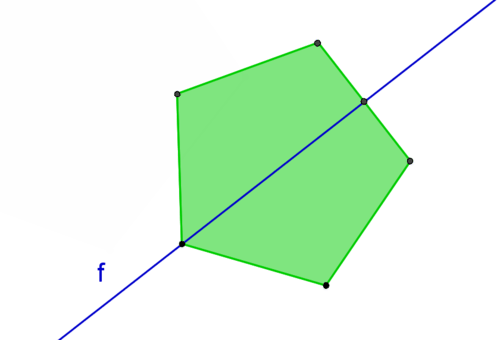
65) Line Symmetry

A figure that can be reflected across a line so that the image coincides with the preimage

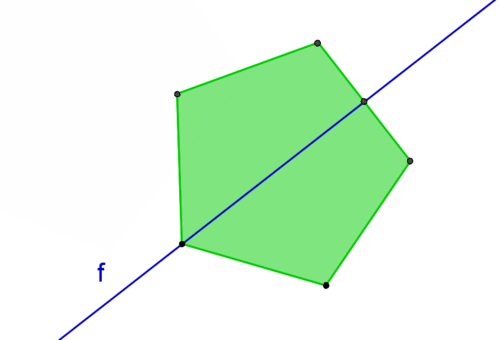
66) Line of Symmetry

A line that divides a plane or figure into two congruent reflected halves

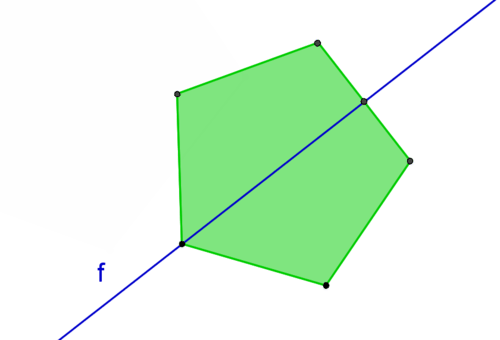
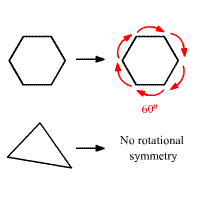
67) Rotational Symmetry

A figure that can be rotated about the point by an angle less than 360 degrees so that the image coincides with the preimage has rotational symmetry

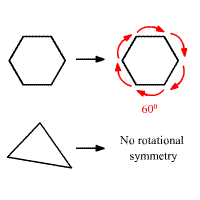
68) Angle of Rotational Symmetry

The smallest angle through which a figure with rotational symmetry can be rotated to coincide with itself

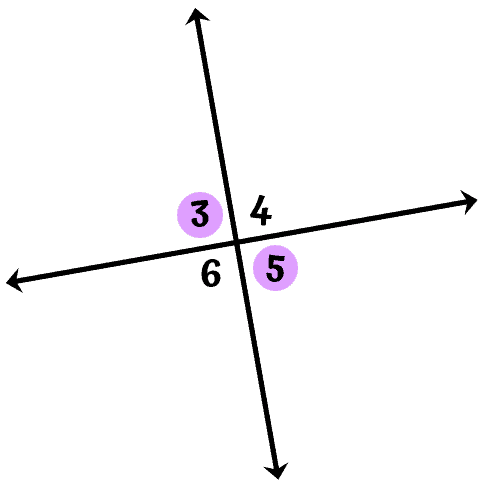
69) Vertical Angles

A pair of non-adjacent angles formed by two intersecting lines

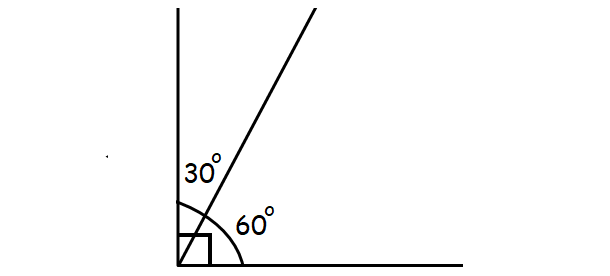
70. Complementary Angles

Two angles whose measures have a sum of 90 degrees

71) Vertical Angles Theorem

If two angles are vertical angles, then the angles are congruent

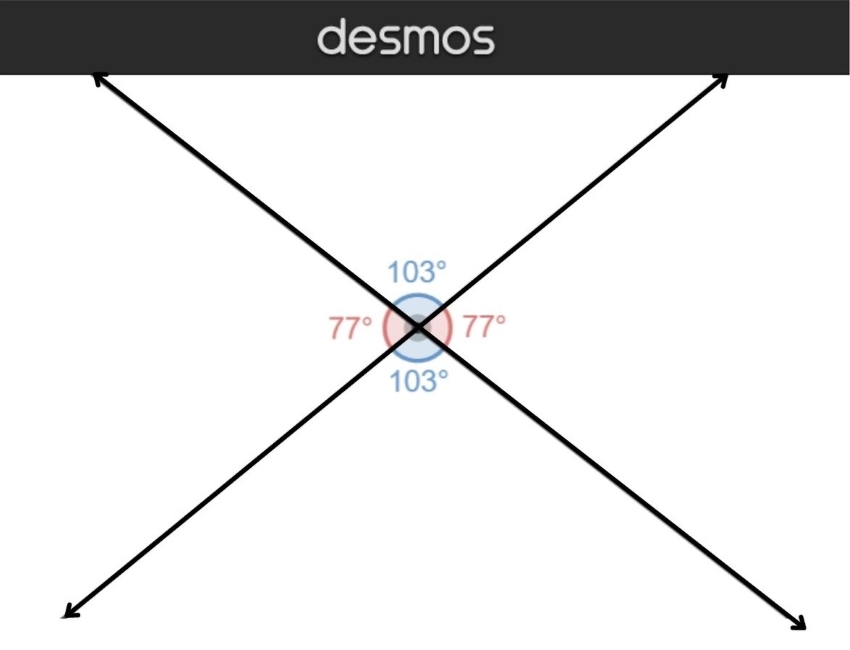
72) Transversal

A line that intersects two coplanar lines at two different points

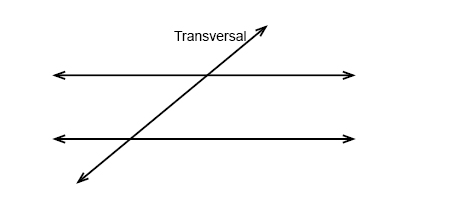
73) Corresponding Angles of Lines Intersected by a Transversal

For two lines intersected by a transversal, a pair of angles that lie on the same side of the transversal and the same side of the two other lines.

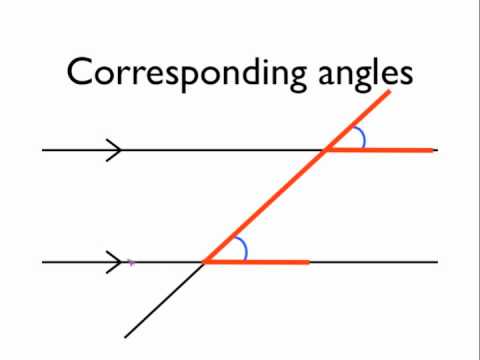
74) Same-Side Interior Angles

For two lines intersected by a transversal, a pair of angles that lie on the same side of the transversal and between the two lines

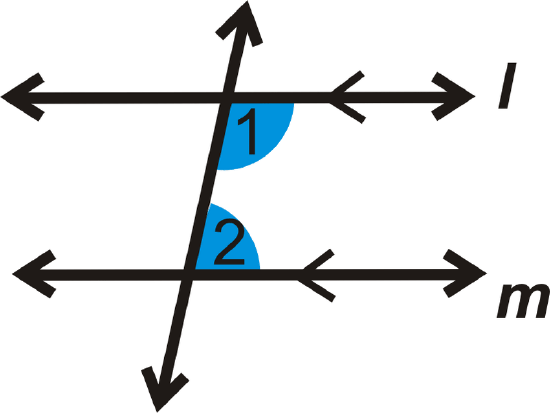
75) Alternate Interior Angles

For two lines intersected by a transversal, a pair of nonadjacent angles that lie on opposite sides of the transversal and between the two other lines

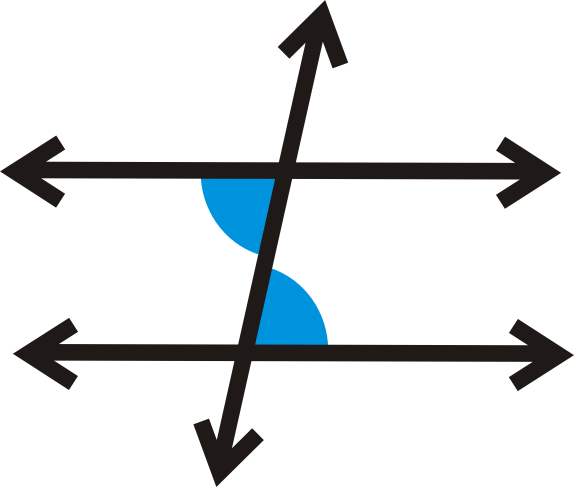
76) Alternate Exterior Angles

For two lines intersected by a transversal, a pair of nonadjacent angles that lie on opposite sides of the transversal and between the two other lines

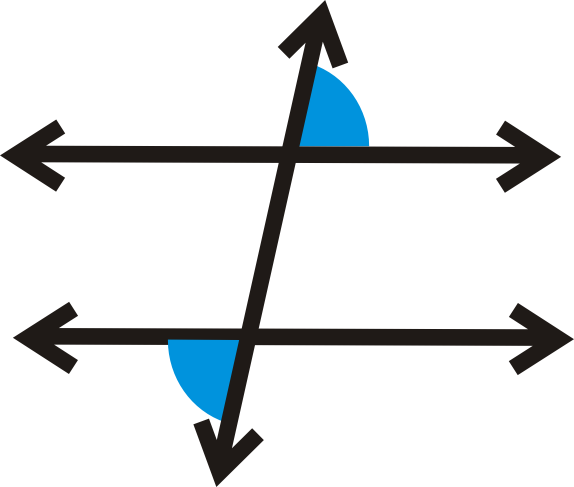
77) Same-side Angle Postulate

If two parallel lines are cut by a transversal, then the pairs of same-side interior angles are supplementary

78) Alternate Interior Angle Theorem

If two parallel lines are cut by a transversal, then the pairs of alternate interior angles have the same measure

79) Corresponding Angles Theorem

If two parallel lines are cut by a transversal, then the pairs of corresponding angles have the measure

80) Converse

The statement formed by exchanging the hypothesis and the conclusion of a conditional statement

Statement: if n+1=3, then n=2

Converse: if n=2, then n+1=3

81) Converse of Same-side Angles

If two lines are cut by a transversal so that a pair of same side interior angles are supplementary, the lines are parallel

82) Converse of the Alternate Interior Angles Theorem

If two lines are cut by a transversal so that any alternate interior angles are congruent, then the lines are parallel

83) Converse of the Corresponding Angles Theorem

If two lines are cut by a transversal so that any corresponding angles are congruent, then the lines are parallel

84) perpendicular Bisector Theorem

If the point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment

85) Converse of the Perpendicular Bisector Theorem

If a point is equidistant from the endpoints of the segment, then it lies on the perpendicular bisector of a segment

86) Corresponding Parts of Congruent Figures

If the figures are congruent, then corresponding sides are congruent and corresponding angles are congruent

87) Biconditional

A statement that can be written in the form of “p if and only if q”

Example:

A figure is a triangle only if it is a three sided polygon

88) Contrapositive

A statement formed by both exchanging and negating the hypothesis and conclusion of a conditional statement

Example:

Statement: n+1=3, then n=2

Contrapositive: n≠2, then n+1≠3

89) ASA Triangle Congruence Theorem

If two angles and the included side of one triangle is congruent to two angles and the included side of another triangle, then the triangles are congruent

90) SAS Triangle Congruence Theorem

If two sides and the included angle of a triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent

91) SSS Triangle Congruence Theorem

If three sides of a triangle is congruent to three sides of another triangle, then the triangles are congruent

92) AAS Triangle Congruence Theorem

If two angles and the non-included side of one triangle is congruent to two angles and the non-included side of another triangle, then the triangles are congruent

93) Hypotenuse

The side opposite the right angle in a right triangle

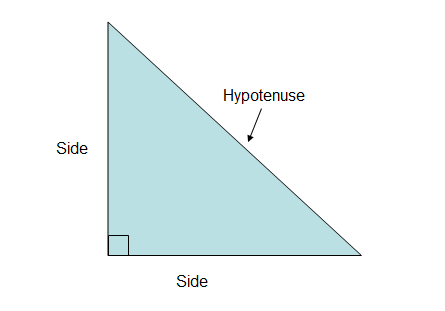
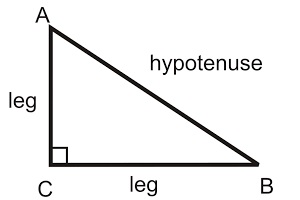
94) Leg of a Right Triangle

One of the two sides of the right triangle that form the right angle

95) Hypotenuse-Leg Triangle Congruence Theorem

If a hypotenuse and a leg of a right triangle is congruent to a hypotenuse and a leg of another right triangle, then the triangles are congruent

96) Interior Angle

The angle formed by two sides of a polygon with a common vertex

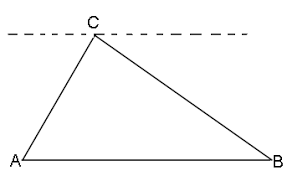
97) Auxiliary Line

A line drawn in a figure to aid in a proof

98) Triangle Angle Sum Theorem

The sum of the angles measures of a triangle is 180 degrees

99) Polygon Angle Sum Theorem

The sum of the measures of the interior angles of a convex polygon with n sides (n-2)180

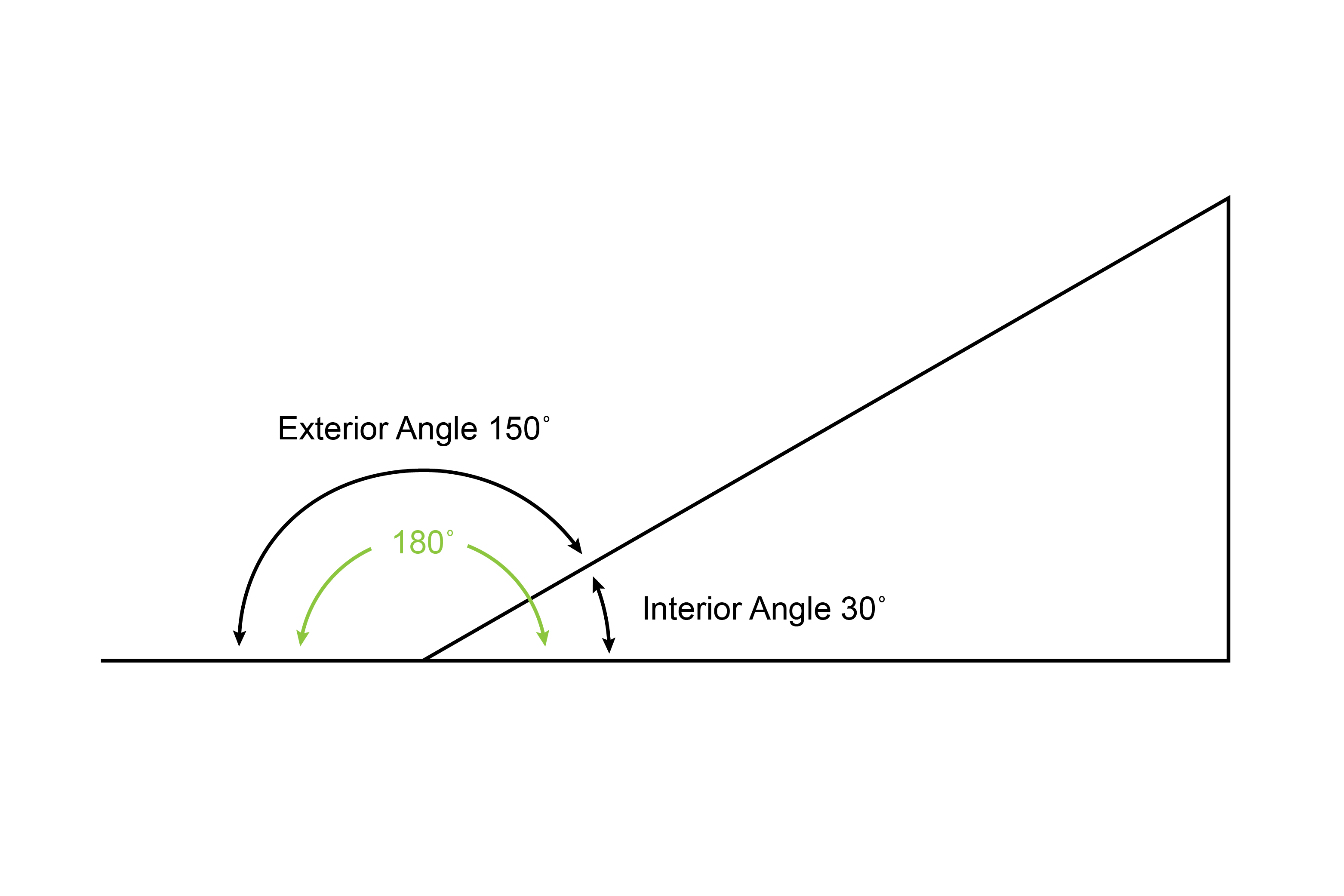
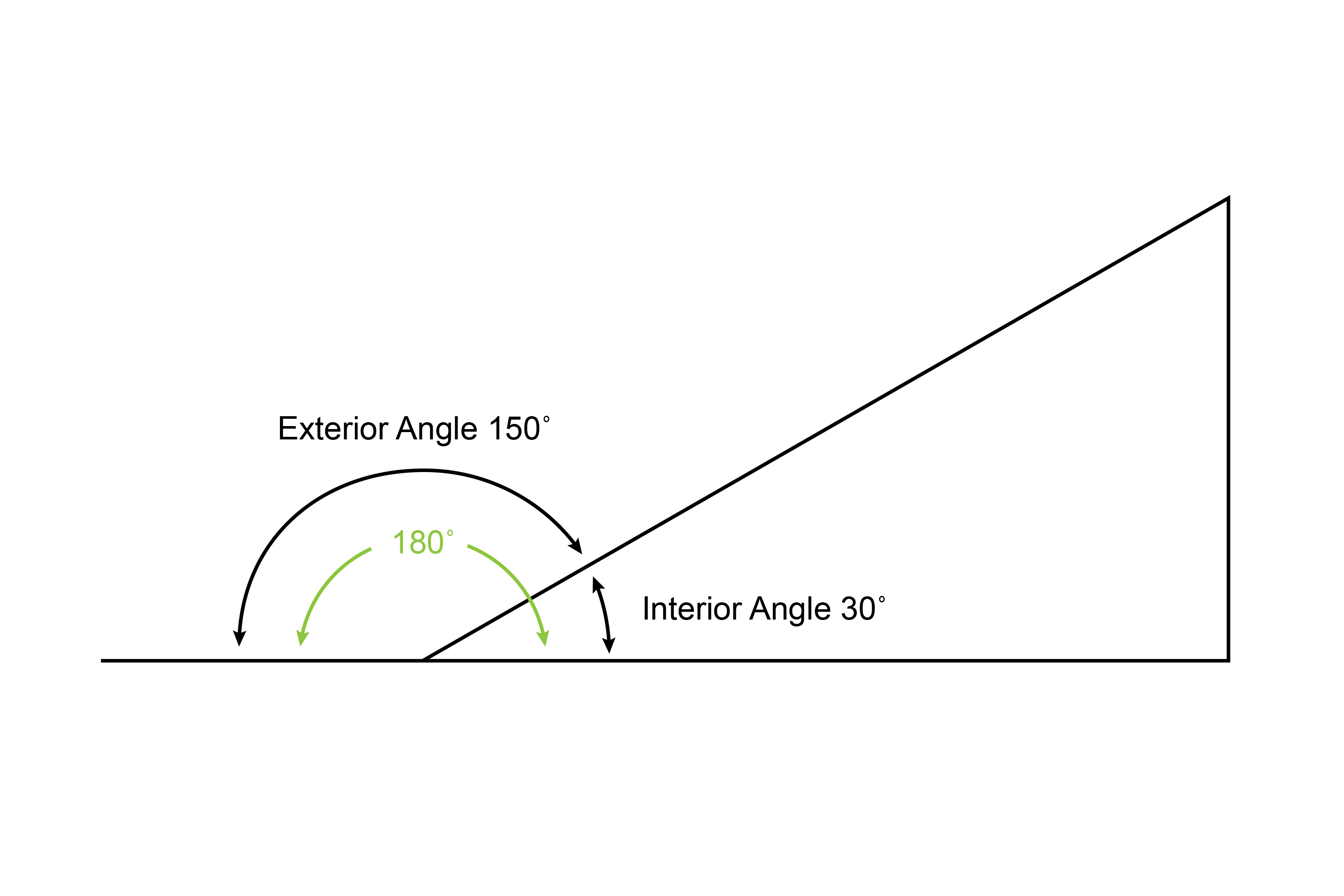
100) Exterior Angle of a Polygon

An angle formed by one side of a polygon and the extension of an adjacent side