Type 1 Type 2 errors and power

P-value

The probability assuming Ho is true that the test stat will take on a value as extreme or more extreme than what we observed

Power

The probability that a fixed a level test will reject Ho when a particular alternative value of the parameter is true.

Steps to calculating power

1. Find the event that causes the test to reject Ho

2. Find the probability of that event, given an alternative value of the parameter is true

Lower power

Larger σ means

Higher Power

Larger sample size means

Higher alpha level means

Higher Power

Higher power

Alternative further from Ho

Type 1 Error

Reject Ho, but Ho is true

Type 2 Error

Accept Ho, Ha is true

Alpha

Probability of a type 1 error

1-Power

Probability of a type 2 error

2 Samp-Z Test and Samp-Z Confidence Interval

σ1 and σ2 are known, x̄₁-x̄₂ follows a normal distribution

2 Samp-T Test and Samp T Confidence Interval

σ1 and σ2 are unknown, x̄₁-x̄₂ follows a t distribution

How to check for normality with a t distribution

Histogram shape for skewness

Comparative box Plot of Outliers

Independence within groups for a t model

Responses in each group are independent of each other

Simple Random Sample

Population is less than 10%

Matched Pairs test

What do you use if the groups are dependent

n<15

No Skewness or outliers

15<n<40

Some skewness but no outliers

n>40

No extreme skewness or outliers

Close to t-distribution

If we can’t assume equal population variance that means it is

Df when you have technology

(n₁-1) + (n₂-1)

Say yes to pooled

If equal variance

Yes

Do you always assume unequal variance?

Larger than

With pooled procedure the Degrees of Freedom is _____ than the Degrees of Freedom for Unequal Variance

Lower, narrower

Pooled procedures makes a ____ rejection rate and _____ interval

p1-p2

Parameter for Inference of 2 Proportions

Statistic for 2-Samp Proportion Problem

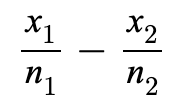
Assumptions for Inference

1. Sampling distribution of p̂₁-p̂₂ is normal

   1. Assess if the sample size is large enough to ensure normality

   2. n₁ p̂_p, n₁(1-p̂_p) and n₂ p̂_p, n₂(1-p̂_p)

2. Independence within groups

   1. Are samples random and is n less than 10% of population

3. Independence between groups.

   1. Responses in one group shouldn’t influence responses in other groups.

We don’t know the parameter p

Pool the sample proportion and replace the standard deviation with standard error if ____

How to check normality for 2-prop Z Int

Check n₁ p̂₁, n₁(1-p̂₁) and n₂ p̂₂, n₂(1-p̂₂) are all more than 10

p-hat of p (p̂_p)

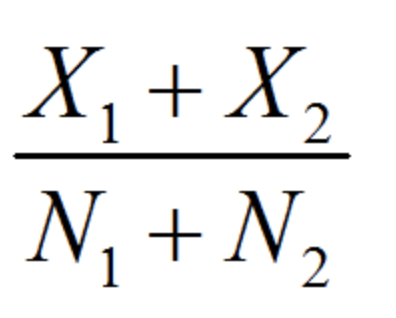
Reject Ho

(p<alpha)

Fail to Reject Ho

(p>alpha)