COSC401 3: Linear Regression

What is linear regression?

A method for modeling the relationship between one or multiple input variables and a continuous output by fitting a straight line (or hyperplane) that minimizes the prediction error.

In linear regression, what is h(x)?

h(x) or h_theta(x) is a linear function of x, for example

h(x) = theta0 + theta1*x1 + theta2*x2 and so on.

What is the intercept term by convention?

theta0 = 1

What is J(theta)?

The cost function, which measures how close h(x) is to y for each x, y pair.

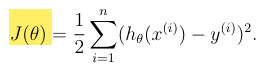
What is our main motivation in “choosing” the theta vector?

To minimise J(theta).

How do we minimise theta (general idea)?

choose a “initial guess“ for theta, then repeatedly change it to make J(theta) smaller with gradient descent.

What is the gradient descent algorithm?

This update is simultaneously performed for all values of j. (0 - d)

alpha is the learning rate

It repeatedly takes a step in the direction of steepest decrease of J.

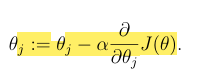
What is the LMS update rule / Widrow-Hoff learning rule for a training set (more than one example)?

Where theta is a vector.

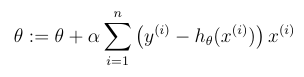
What are the two main gradient descent variants?

• batch: scans entire training set before taking a single step, but always converges

• stochastic: each time we encounter a training example, update the parameters. gets close to the minimum much faster, but may never converge, instead oscillating.

In practice, stochastic is preferred, especially when the training set is large

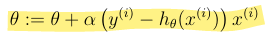
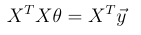
Describe each part of this:

X: design matrix, n-by-d(+1) where each row is the input of a training example

y: vector of targets

theta: as usual - and solving for theta here gives us the value of theta that minimises J

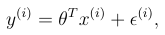
What is this?

A probabilistic assumption of the relation between X and y.
epsilon is an error term that captures unmodeled effects or random noise

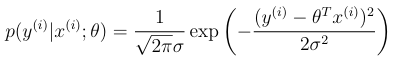
What is this?

A result of assuming that that epsilon is distributed independently and identically. (IID) according to a normal distribution with mean 0 (variance unimportant).

The equation describes the probability distribution of y given x.

What function allows us to explicitly view the probability distribution of y given x as a function of theta?

The likelihood function

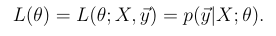
How should we choose theta regarding the likelihood function?

We should MAXIMISE L(theta).

Why can we use the log likelihood? And why?

Because we can maximise any strictly increasing function of L(theta), which log(L(theta)) is.

We do this to make the derivations a lot simpler, as the log of a product is the sum of the logs.

Maximising the log likelihood gives the same answer as _?

Minimising the least-squares cost function.