Theory Data Algorithms & Structures
1/63
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
64 Terms
What are the basic components of a linked list?
Data members for the information to be stored and a link to the next item.
What is a node used for in a linked list?
To store the information and the link to the next item.
A node in a linked list is like a box that holds:
the data desired to keep
a pointer to the next box
A linked list is different from an array because
An array is fixed in size, but a linked list is dynamically sizable.
Also, a linked list allocated memory individually.
An array pre-allocated a continuous block of memory.
In addition to the info and link components, the linked list must also contain what other components?
Head and tail pointers to the first and last nodes
Tail
Points to the last node in a linked list (NULL/nullptr)
Head
Points to the first node of the list.
What is the proper code for accessing the information of the second item in a linked list?
‘head’ points to the first node
‘head.link’ points to the second node
‘info’ retrieves the data stored in the second node
Giving the fixed size of an array is not important. Which class is more efficient at storing and retrieving information?
An array because of the reduced code and efficient storage allocation.
Which is suitable for quick data access.
What does the following fragment of code do with the linked list?
current = head;
while (current != null) {
current = current.link;
}
It traverses the list.
By moving from one node to the next —> it goes through all the items in the list and checks or does something with each item.
Which of the following code fragments properly inserts 50 into the linked list at the position after node p?
A. newNode = new Node();
newNode.info = 50;
p.link = newNode;
B. newNode = new Node(50, p);
C. newNode = new Node();
newNode.info = 50;
p.link = newNode;
D. B and C.
(D) B and C because:
B creates a new node with the value of 50 and inserts it after node p
C creates a new node with the value of 50 and inserts it after node p (‘p.link'). Node p’s link is then updated to point to the new node.
Internally, a linked list is implemented with an array for the storage of the information?
False, because a linked list actually uses nodes to organise and link data together in a flexible manner.
A linked list must contain a maximum size component to manage the last item?
False, because a linked list can actually dynamically adjust in size and the last item is managed through the structure’s links rather than a maximum size constraint.
What is the difference between building a linked list FORWARD and BACKWARDS?
Nothing, only the insertion of the information at the head or tail of the linked list.
FORWARD linked lists —> inserts data at the head; allowing for traversal from head to tail.
BACKWARD linked lists —> inserts data at the tail; allowing for traversal from tail to head.
What does ADT stand for?
Abstract Data Type
An ADT defines the behaviour of objects through operations without specifying their internal implementation
—> mentions WHAT operations to perform; not HOW to implement them!
What is the purpose of using an ADT for the linked list class?
To force a specific set of methods to be used for the subclasses.
Also, ADT provides an abstract blueprint for how the linked list should behave.
The instance variables first and last (or head and tail) below to which class of a linked list?
Class LinkedListClass
Because they are used to manage and maintain the structure of the linked list.
Wat should the default constructor of the LinkedListClass perform?
Initialize the first and last (or head and tail) and set count to zero.
By doing so, this sets up an empty linked list as the initial state when an instance of the class is created.
What is a circular linekd list?
The last node in the linked list points to the first.
This created a closed loop/cycle which allows for continuous traversal from the last node to the first node in a circular manner.
In linked lists there are no NULL links
Circular linked list
Because the last node’s link points back to the first node; creating a continuous loop within the linked list.
In a stack the command to access nth element from the top of the stack S will be
S[Top-n]
Because it considers the top element as 1 and subtracts n to locate the desired element.
If yyy, xxx and zzz are the elements of a lexically ordered binary tree, then in preorder traversal which node will be traverse first
yyy
Because in a lexically ordered binary tree, the node that will be traversed first in a preorder traversal is the leftmost node (YYY), as it starts with the root node and goes from left to right.
In a balance binary tree the height of two subtrees of every node can not differ by more than
1
Because this property ensures that the tree stays approximately balanced.
The result of evaluating prefix expression */b+-dacd where a=3, b=6, c=1, d=5, is
10
Because operators act on the two nearest values to the right.
/b+-dacd = */b+-(d-a) cd
= {b/[(d-a) + c] * d
= {6/[5 - 3 + 1] * 5
= 6/3 * 5
= 10
In array representation of binary tree the right child of root will be at location of
2
Because the array is usually indexed starting from 0 and the left child is stored at index 2i+1 and the right child at 2i+2
—> where i is the index of the parent node.
The total number of comparisons in a bubble sort is
O(n^2)
Because in the worst case, it compares every pair of elements in the input list, and the number of comparisons is proportional to n(n-1)/2 which simplifies O(n^2)
The dummy header in linked list contain
First record of the actual data
Write the output of the following program:
int a[ ] = {1, 2, 3} * p;
Run time error (technically a compile term error)
If the out degree of every node is exactly equal to M or 0 and the num ber of nodes at level K is
Mk-1 [con sider root at level 1], then tree is called as
(i) Full m-ary try
(ii) Com plete m-ary tree
(iii)Positional m-ary tree
A. Only (i)
B. Only (ii)
C. Both (i) and (ii)
D. Both (ii) and (III)
C. Both (i) and (ii).
Because:
(i) M-ary try —> a tree where each node ha either M or zero children.
(ii) Complete m-ary tree —> a tree where all levels are completely filled except possibly the last level which is filled from left to right.
A queue has configuration a, b, c, d. To get configuration d, c, b, a. One needs a minimum of
3 deletions and 3 additions
3 deletions to remove a, b, c
3 corrections to add d, c, b
Number of possible ordered trees with 3 nodes A, b, C
6
Number of swapping, operations need to sort numbers 8, 22, 7, 9, 31, 19, 5, 13 in ascending order using bubble sort:
14
First pass: 8, 22 (swap) → 22, 7 (no swap) → 22, 9 (no swap) → 22, 31 (swap) → 31, 19 (no swap) → 31, 5 (no swap) → 31, 13 (no swap)
Second pass: 8, 7 (no swap) → 8, 9 (swap) → 9, 19 (swap) → 19, 5 (no swap)
Third pass: 7, 8 (swap) → 8, 9 (swap)
Fourth pass: 7, 8 (swap)
Fifth pass: no swap needed = list sorted
Consider two sorted lists of size L1, L2. Number of comparisions needed in worst case my merge sort algorithm will be
L1 + L2 - 1
To merge 2 lists of size m and n: m + n + 1 comparisons in worst case.
To merge 2 at a time: take the smallest size lists first
A hash table with 10 buckets with one slot per bucket is depicted in following diagram. Symbols S1 to S7 are initially entered using a hashing function with linear probing. Maximum number of comparisons needed in searching an item that is not present is
0 I S7
1 I S1
2 I
3 I S4
4 I S2
5 I
6 I S5
7 I
8 I S6
9 I S3
5
In a hash table with 10 buckets and linear probing, the maximum number of comparisons needed in searching for an item that is not present is 5.
Formula in linear probing max. number of comparisons = n + 1
= 4 + 1 = 5
To minimize comparisons: start searching from an index that covers the most elements
if start is at index 8: 4 indices searched (8, 9, 0, 1)
then check next index: empty
4 comparisons + 1 = 5 comparisons
A full binary tree with 6 non-leaf contains a maximum of
13 nodes
2n + 1 = 2 × 6 + 1 = 12 + 1 = 13
A binary search tree is generated by inserting in order the following integers: 50, 15, 12, 25, 40, 58, 81, 31, 18, 37, 60, 24. The number of the node in the left subtree and right subtree of the root is
(8, 3)
Because when the given integers are inserted in order into a binary search tree:
Left subtree of the root will have 8 nodes → 12, 15, 18, 24, 25, 31, 37, 40
Right subtree of the root will have 3 nodes → 58, 60, 81
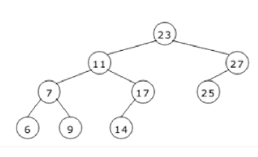
If this tree is used for sorting, then new no 8 should be placed as the
Left child of the node labeled 9
Because binary search tree used for sorting place:
smaller values to the left of the node
larger values to the right of the node
8 < 9 so left child of node 9
When you construct a BST with the preorder traversal of a binary search tree 10, 4, 3, 5, 11, 12,21,36, then which of the following are leaf nodes?
3, 5, 36
Because the leaf nodes in a BST are nodes that do not have children.
In the given preorder traversal, leaf nodes = 3, 5, 36
Because these nodes do not have any children in the BST
Suppose the numbers 7, 5, 1, 8, 3, 6, 0, 9, 4, 2 are inserted in that order into an initially empty binary search tree. The binary search tree uses the usual ordering of natural numbers. Will the in-order traversal sequence of the resultant tree be the same for the numbers in the sequence 9, 7, 5, 1, 8, 3, 2, 6, 0, 4?
Yes
7, 5, 1, 8, 3, 6, 0, 9, 4, 2
Since the in-order traversal sequence of a BST is determined by the order in which elements are inserted,
Resulting in a specific structure of the tree
9, 7, 5, 1, 8, 3, 2, 6, 0, 4
When this is inserted in the same order → it will result in the same structure of the three
So the in-order traversal sequence of the resulting tree will be the same for both sequences.
The following numbers are inserted into an empty binary tree and binary search tree in the given order: 20, 10, 1, 3, 5, 15, 12, 16, 34, 87, 35. The height of the binary tree and binary search tree, respectively, is:
4, 3
Height of binary tree = 3
root node = 20
lead nodes = 5, 15, 12, or 16
Because the longest path from root to leaf is 3 steps
Height of binary search tree = 4
root node = 20
leaf = 87
Because the longest path from root to a leaf is 4 steps
The preorder traversal sequence of a binary search tree is 30, 20, 10, 15, 25, 23, 39, 35, 42.
Which one of the following is the postorder traversal sequence of the same tree?
A. 10, 20, 15, 23, 25, 35, 42, 39, 30
B. 15, 10, 25, 23, 20, 42, 35, 39, 30
C. 15, 20, 10, 23, 25, 42, 35, 39, 30
D. 15, 10, 23, 25, 20, 35, 42, 39, 30
C. 15, 20, 10, 23, 25, 42, 35, 39, 30
root = node 30
left subtree = nodes 20, 10, 15, 25
right subtree = nodes 39, 35, 42
left child = node 25
Construct a binary tree by using inorder and preorder sequences given below.
Inorder: D, B, H, E, I, A, F, C, G
Preorder: A, B, D, E, H, I, C, F, G
Find the postorder traversal
A. D, H, E, I, B, F, G, C, A
B. A, C, G, F, B, I, E, H, D
C. D, H, I, E, B, F, G, C, A
D. D, H, I, E, G, F, B, C, A
C. D, H, I, E, B, F, G, C, A (postorder traversal found by visiting nodes)
Because it is obtained by first contracting the tree and then traversing it in the left to right manner.
root = node A
left subtree = nodes B, D, E, H, I
right subtree = nodes C, F, G
Which of the two key sequences construct the same BSTs? Select the ones you like
A. A1[ ] = {8, 3, 6, 1, 4, 7, 10, 14, 13}
A2[ ] = {8, 10, 14, 3, 6, 4, 1, 7, 13}
B. B1[ ]= {15, 10, 25, 23, 20, 42, 35, 39, 30}
B2[ ] ={15, 20, 10, 23, 25, 42, 35, 39, 30}
C. C1[ ]={7, 5, 1, 8, 3, 6, 9, 4, 2}
C2[ ]={ 9,7, 5, 1, 8, 3, 2,6, 4}
D. D1[ ]={15, 10, 25, 23, 20, 42, 35, 39, 30}
D2[ ]={ 15,35,39,10,25,20,23,42,30}
A. A1[ ] = {8, 3, 6, 1, 4, 7, 10, 14, 13}
A2[ ] = {8, 10, 14, 3, 6, 4, 1, 7, 13}
Because both key sequences A1[ ] and A2[ ] construct the same BST.
The order of elements in key sequences does NOT matter when creating BST, as long as the elements themselves are the same.
What is the maximum height of any AVL tree with 7 nodes? Assume that the height of a tree with a single node is 0.
3
Because an AVL tree is a self-balancing BST
Height from the root (node 1) to the farthest left node (node 4, 5, 6, or 7) = 3
AVL tree
A self-balancing binary search tree where the heights of the left and right subtrees of any node differ by at most one.
Root node
The topmost node in a tree structure, from which all other nodes are descendants.
Insert the following sequence of elements into an AVL tree, starting with an empty tree:
10, 20, 15, 25, 30, 16, 18, 19
after deleting node 30 from the AVL tree then the root node of the resultant tree is
18
Show the result when an initially empty AVL tree has keys 1 through 8 inserted in order. Then the node in the last level will be
8
Because when keys 1 through 8 are inserted into an initially empty AVL tree in order:
the tree remains balanced
each level has as many nodes as possible
So last level will have just one node = 8
AVL property
The property that ensures the heights of the left and right subtrees of any node in an AVL tree differ by at most one.
AVL tree of height 4 contains ……………. minimum possible number of nodes:
12
N(height) = N(height - 1) + N(height - 2) + 1
N(4) = N(4- 1) + N(4 - 2) + 1
N(4) = 7 + 4 + 1
N(4) = 8
Where N(0) = 1, N(1) = 2
To restore the AVL property after inserting an element, we start at the insertion point and move towards the root of that tree. Is this statement true?
True
Because after inserting an element into an AVL tree, we check and adjust nodes along the path to the root to maintain the tree’s balance.
Given an empty AVL tree, how would you construct an AVL tree when a set of numbers are given without performing any rotations?
Find the median of the set of elements given, make it a root.
First find the median of the given elements
Set the median as the root for balance
Elements < median → go to the left
Elements > median → go to the right
Repeat for left and right subtrees to build a balanced AVL without rotations.
Heap
A specialized tree-based data structure that satisfies the heap property, where the parent node is either greater than or equal to (in a max heap) or less than or equal to (in a min heap) its children.
Max heap
A type of heap where the parent node is greater than or equal to its children.
The balance factor of node A was 0 and, a node was inserted to the left of node A then:
It is required to balance the Parents of node A
When a node is inserted to the left of node A = imbalance in parent node
Because the left subtree of the parents becomes heavier than the right subtree
AVL is traversed in the following order recursively: right, root, left. The output sequence will be in
Descending order
right subtree is visited first
root node is visted next
left subtree is visted last
= descending order
State the complexity of the algorithm given below.
int function(vector<int> arr) {
int len=arr.length();
if(len==0) return;
temp=arr[len-1];
arr.pop_back();
return temp;
}
O(1)
Because the algorithm performs a fixed number of operations (regardless of the size of the input vector)
It checks the length of the vector, performs a single operation to retrieve the last element, and removes the last element from the vector.
Leaf node
A node in a tree that does not have any children.
An array consists of n elements. We want to create a heap using the elements. The time complexity of building a heap will be in the order of
O(n*logn)
It is determined by the number of swaps and comparisons to satisfy heap property
n = number of elements in array
O(n*logn) because height of a heap is logarithmic with respect to n
If we implement heap as a maximum heap, adding a new node of value 15 into it. What value will be at leaf nodes of the left subtree of the heap?
2, 7, 3
When a node is added to a max heap, it is added at the next free leaf node from left to right
What will be the position of 65 when a max heap is constructed on the input elements
5, 70, 45, 7, 12, 15, 13, 65, 30, 25?
Second level
Because in a max heap, the largest element is always the root and the elements are organised in a complex binary tree.
Since 65 is not the largest node, it is NOT the root.
Second level contains the left and right children of the root node
Does there exist a heap with seven distinct elements so that the In order traversal gives the element in sorted order?
No
Because elements in a heap are arranged in a specific order based on their priority (highest priority element at the root).
→ A heap does NOT guarantee sorted order in it in-order traversal because it follows a specific pattern of visiting nodes.
Given a binary-max heap. The elements are stored in an array as 25, 14, 16, 13, 10, 8, 12. What is the content of the array after two delete operations?
14, 13, 12, 8, 10
In a binary max heap, the max element = the root
Delete (removing the root element) = 25 & replace it with the last element of the array = 12
Array now: [16, 14, 12, 13, 10, 8]
Delete (removing the new root element) = 16 & replacing it with the last element = 8
Array now: [14, 13, 12, 8, 10]
Consider the following array of elements 89, 19, 50, 17, 12, 15, 2, 5, 7, 11, 6, 9, 100, 98 then the minimum number of interchanges needed to convert it into max-heap is
5
To convert the given array to a max heap:
Arrange elements given so each parent node is > or = to its children.
Minimum number of interchanges:
Count the number of times needed to swap elements to meet condition.