vecteurs et plans

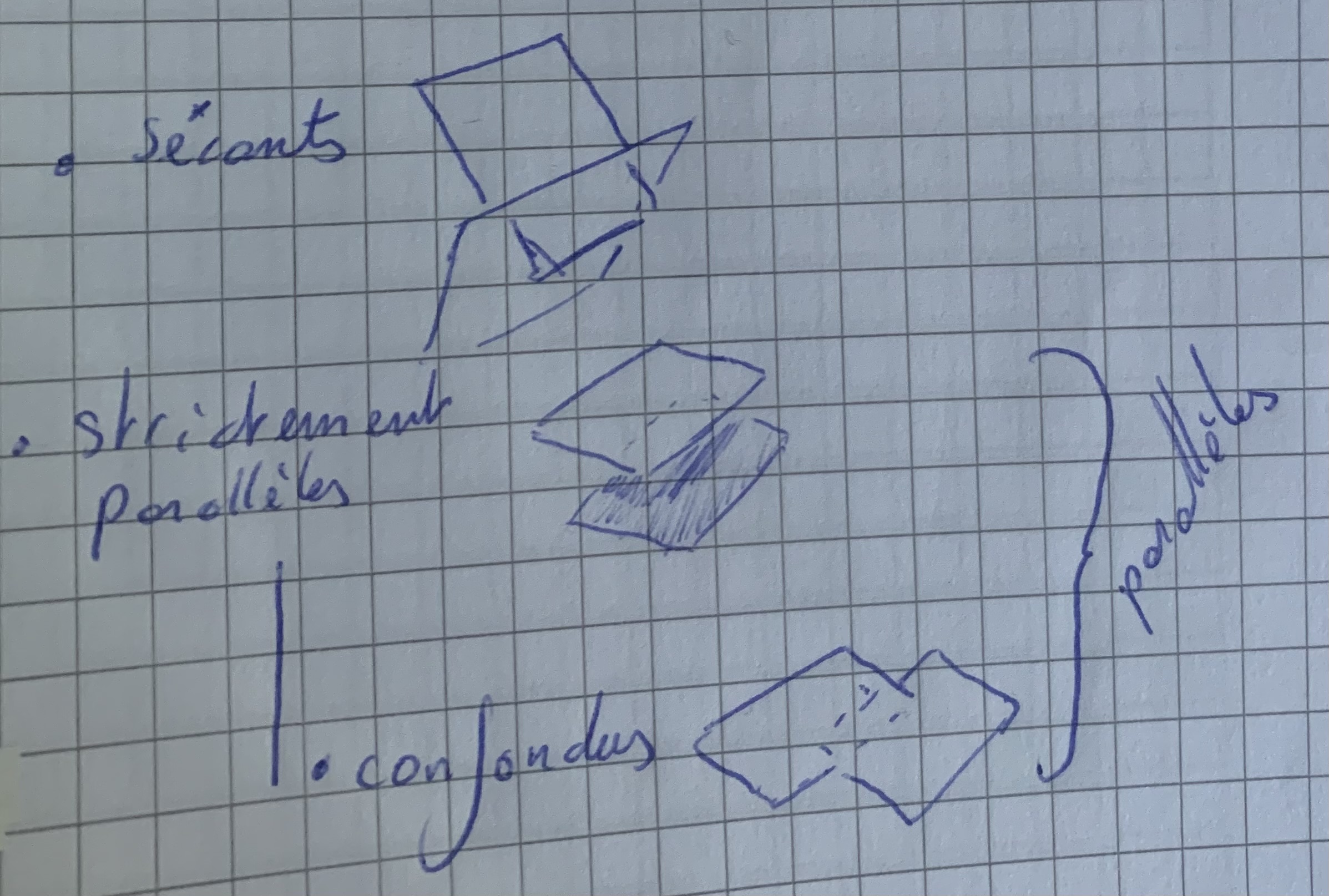
Quels sont les quatre cas de figure de positions relatives de 2 droites dans un espaces en 3D ?

Quels sont les trois cas de figure de positions relatives d’une droite et un plan ?

Quels sont les trois cas de figure de positions relatives de deux plans ?

Quelle est la difference entre

(XY)

Et

(XYZ)

(XY) → droite passant par les points X et Y

(XYZ) → plan passant par les points X, Y et Z

Théorème des milieux ?

Dans un triangle, si un segment passe par les milieux de deux côtés, alors elle est parallèle au troisième côté et en mesure la moitié.

En passant par c

Selon la relation de Chasles : \overrightarrow{AG} = ?

\overrightarrow{AG}=\overrightarrow{AC}+\overrightarrow{CG}

Avec toujours AG\le AC+AG

Et AG=AC+AG ssi C\in\left\lbrack AG\rbrack\right.

Déterminer le barycentre du système (A, 3) (B, 2)

On a notre segment [AB] avec 3A pesant 2B

On veut déterminer le barycentre G tel que

3\overrightarrow{GA} + 2\overrightarrow{GB} = \overrightarrow{0}

Chasles → faire disparaître un vecteur en le remplaçant par le premier vecteur + le système

3\overrightarrow{GA} + 2\overrightarrow{GA}+2\overrightarrow{AB} =\overrightarrow{0}

5\overrightarrow{GA} + 2\overrightarrow{AB} =\overrightarrow{0}

5\overrightarrow{GA} =-2\overrightarrow{AB}

\overrightarrow{GA} =2/5 \overrightarrow{BA}

Def vecteurs colinéaires

\overrightarrow{u}=k\cdot\overrightarrow{v} Avec k\in\mathbb{R}

Alors \overrightarrow{u} et \overrightarrow{v} sont colinéaires

Trouver le point d’intersection I d’une droite et d’un plan sécants ?

I est l’intersection de la droite et d’une autre droite qui elle fait partie du plan

• Soit cette autre droite est évidente

• Soit on crée cette autre droite par l’intersection du plan avec un autre plan qui lui inclue la première droite

Montrer que deux plans sont sécants

Trouver un point commun aux deux plans

→ prouver que ces plans ne sont pas confondus = trouver un point de l’un n’appartenant pas à l’autre

Construire la droite (d) d’intersection de deux plans

On trouve 2 points A et B communs aux deux plans, (d) est alors la droite (AB)

• soit ces points sont évidents

• Soit pour trouver un point on construit l’intersection de deux droites appartenant chacune à un plan

Ça veut dire quoi quand on voit \overrightarrow{AM}=\frac12\overrightarrow{AB} ?

M est le milieux du segment [AB]

De quoi ne faut-il pas abuser lors d’une démonstration ?

Des pronoms personnels

On n’écrit pas « ils sont colinéaires » mais « les vecteurs truc et truc sont colinéaires »

Si \overrightarrow{AB}=\overrightarrow{CD} alors ?

ABDC est un parallélogramme

-\overrightarrow{AB} = ?

\overrightarrow{BA}

Comment s’appelle ce vecteur : \overrightarrow{0} ?

Vecteur nul

Règle du parallélogramme

Montrer que (AB) et (CD) sont parallèles ?

Montrer que \overrightarrow{AB} et \overrightarrow{CD} sont colinéaires

Montrer que A, B et C sont alignés ?

Montrer que \overrightarrow{AB} et \overrightarrow{AC} sont colinéaires

Si

\overrightarrow{AB}=k\cdot\overrightarrow{AD} et \overrightarrow{AC}=k\cdot\overrightarrow{AE}

Alors (BC) et (DE) sont quoi ?

Et selon qui ?

→ A, B et D sont alignés

→ A, C et E sont alignés

Il existe un triangle ADE donc selon Thalès

(BC)//(DE)

Deux manières de définir un plan ?

• Donner trois points

• Donner deux vecteurs non-colinéaires + un point

Ex. (OIJ) = (O\overrightarrow{i}\overrightarrow{j})

Avec \overrightarrow{i}=\overrightarrow{OI} et \overrightarrow{j}=\overrightarrow{OJ}

Coordonnées de \overrightarrow{AB} ?

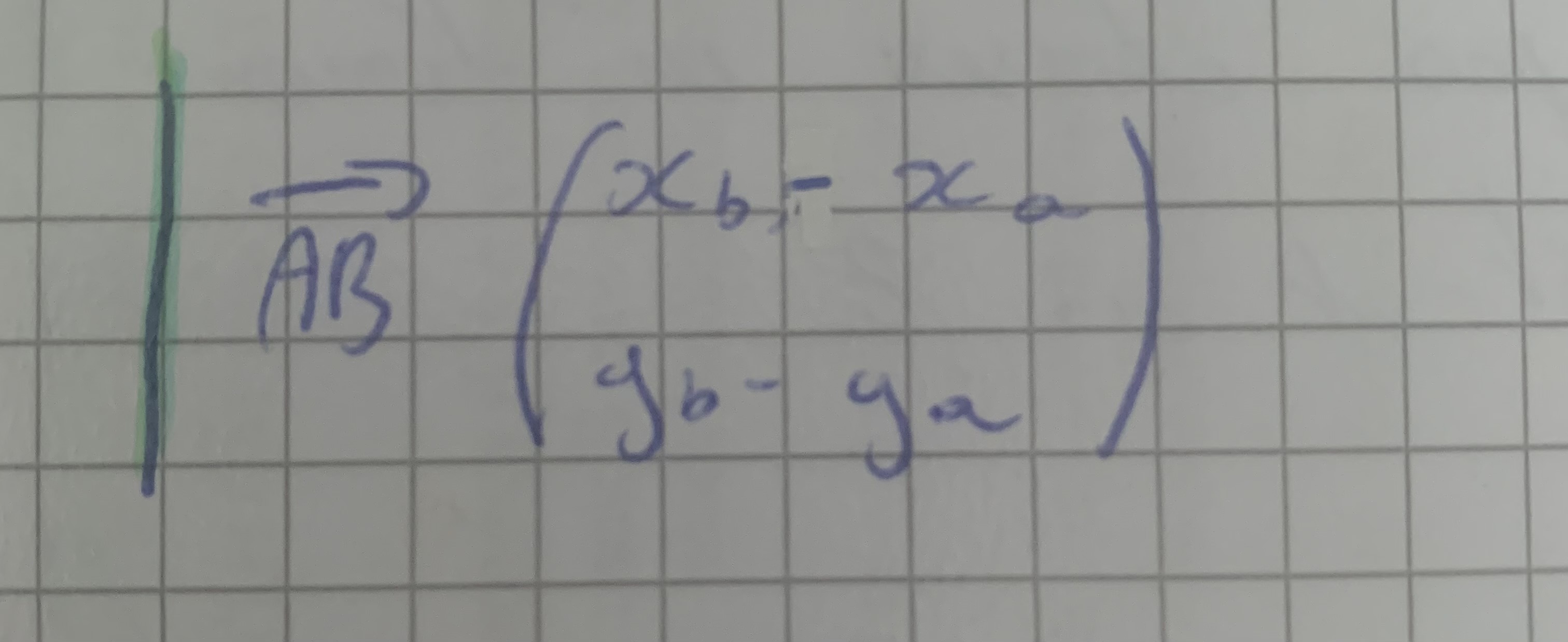
Voir que deux vecteurs sont colinéaires grâce à leurs coordonnées ?

xy’ = x’y

Soit xy’ - x’y = 0

Ou alors il existe un réel k tel que \overrightarrow{u}=k\cdot\overrightarrow{v}

Formule de ||\overrightarrow{u}|| ?

u=\sqrt{x^2+y^2}

Voir que des vecteurs sont orthogonaux grâce à leurs coordonnées ?

x\times x^{\prime}+y\times y^{\prime}=0

Deux manières de voir si trois vecteurs sont coplanaires

• le premier peut il s’écrire comme la combinaison linéaire des deux autres ? (Utiliser un système d’équation et le résoudre avec des matrices c trop easy)

• Si tous les vecteurs partent du même point, les 4 points sont ils coplanaires

Comment faire un repère de l’espace en 3D ?

Un point et trois vecteurs non coplanaires

Base de l’espace vs repère de l’espace

Base de l’espace = 3 vecteurs non coplanaires

Repère de l’espace = base de l’espace + 1 point

Comment écrire que les points ABD et E ne sont pas coplanaires

On peut écrire E\notin(ABD)

E n’appartient pas au plan (ABD)

Comment s’appellent les 3 axes dans un repère de l’espace ?

(0; abscisse/x ; ordonnée/y ; z)

Quand un repère est donné avec des vecteurs comment écrit on les coordonnées ?

1 vecteur = 1 unité

Coordonnées de points vs de vecteurs ?

Point → matrice ligne

Vecteur → matrice colonne

Trouver un point à partir d’une égalité de vecteurs ?

Ex. Trouver J en sachant que \overrightarrow{FJ}=2\overrightarrow{FI}

• écrire les coordonnées (sauf pour le point qu’on ne connaît pas)

• Écrire les 3 équations pour x y et z et les résoudre comme un système

Comment s’écrit l’axe des x ?

A B S C I S S E S

Dans un repère (2D ou 3D) les vecteurs sont ils forcément orthogonaux ?

Non

Manière stylée d’écrire un système

Avec \sum et \sum\lrArr

3 manières de résoudre un système d’équations ?

• Par substitution

• Par combinaison linéaire

• Grace à la règle de Cramer

C’est quoi un système 2×2 ?

2 équations

2 inconnues

Comment s’appelle cette figure ?

Tétraèdre

Def médiane

Médiane issue d’un sommet S relie ce sommet au milieu du côté opposé

Centre de gravité d’un triangle ?

\overrightarrow{GA}=\overrightarrow{GB}=\overrightarrow{GC}

G se trouve à l’intersection des trois médianes du triangle

Sur chaque médiane G se trouve à 2/3 du sommet et 1/3 du milieu du côté opposé

Montrer que 4 points A M C et E sont coplanaires ?

Monter que les vecteurs \overrightarrow{AM} \overrightarrow{AC} et \overrightarrow{AE}sont coplanaires