FDA - Exploratory Data Analytics, week 1

Categorical (qualitive) data 

No numeric value

Categorical (qualitive) data  → Nominal data

Two or more outcomes with no natural order (blond, brown, green hair)

Categorical (qualitive) data → Ordinal data

Two or more outcomes with a natural order (good, medium, bad)

Categorical (qualitive) data → Dichotomous data 

Two possible outcomes (true/false, yes/no)

Numerical (quantitative) data

With a numeric value

Numerical (quantitative) data → Continuous data

Can attain any value

Numerical (quantitative) data → Continuous data → Interval data

No fixed zero point (clock time, birth year)

Numerical (quantitative) data → Continuous data → Ratio data

With fixed zero point (money, distance, time duration)

Numerical (quantitative) data → Discrete data

Can only attain certain values (number of...)

Cyclic data

Has a circular order and allows some numeric operations (days of week, wind direction)

One-dimensional data

One value

example: make a histogram of hight of people. There are 8 people with a hight of 1.80m, 1.80m is a value but 8 people is just a count and not a value.

Two-dimensional data

Two values

Example: temperature and ice cream sales. Temperature is one value and the amount of sales is the other value

Dot plot

• One value, one-dimensional

• To find clusters, ouliers

Scatter plot

• Two values(numeric), two-dimensional

• Investigates relations and used to see if there are outliers

Histogram

• One value(numeric), one-dimensional

• Data is split in bins(=staven)

  • To understand the distribution of the data

Bar chart

• Two values(1 categorical, 1 numeric), two-dimensional

• To look up and compare values

Mean

Average

(1 + 5 + 8 + 2) / 4 = 4

Median

The value separating the lower half from the higher half

100, 160, 200, 360: median = 180

10, 20, 30, 40, 50: median = 30

Mode

Most frequently occurring value

1, 3, 1, 5, 2, 3, 1: mode = 1

Range

maximum - minimum

60, 70, 75, 90, 95

→ 95 - 60 = 35, range = 35

Interquartile range

Median Q3 - median Q1

Sample variance

Tells you on average, how far the data values from the mean, squared

→ the higher the statistics the more spread/variability in the data

Sample standard deviation

Tells you how many units it is away from the mean

→ the higher the statistics the more spread/variability in the data

Median absolute deviation

Measures how far data values typically are from the median

→ the higher the statistics the more spread/variability in the data

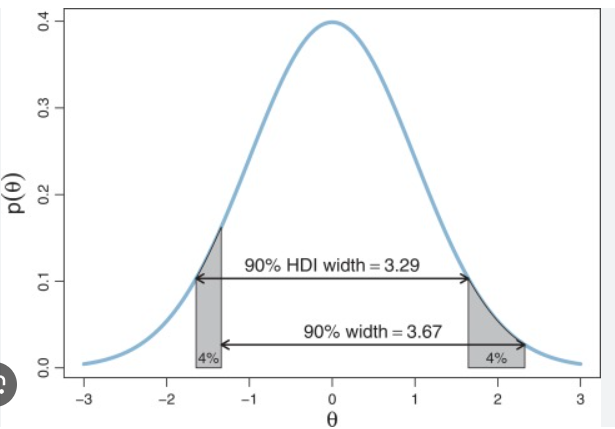
Unimodal distribution (1 peak)

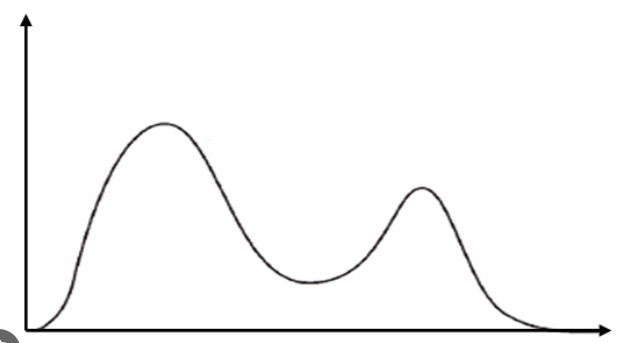
Bimodal distribution (2 peaks)

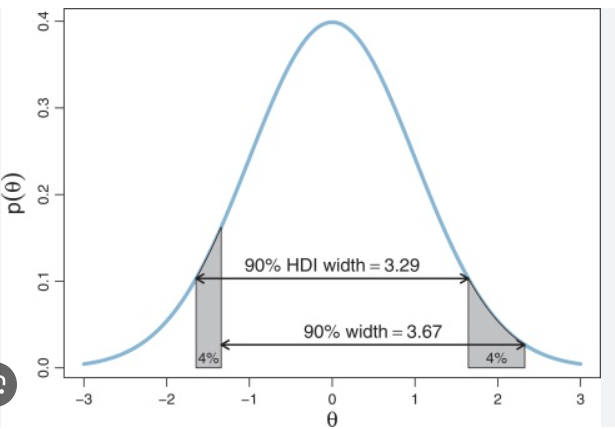
Symmetric distribution

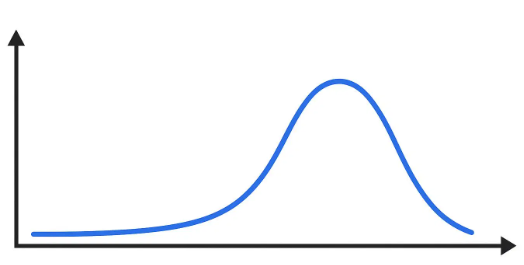
Left - skewed (negative)

mean<median<mode

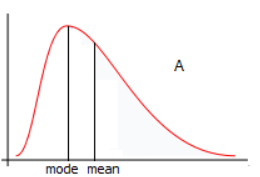
Right - skewed (positive)

mode<median<mean