1. Modelling in Engineering

LO: 1. Model classification 2. Complexity 3.System Identification in Modelling

Compare deterministic models to probabilistic / stochastic models

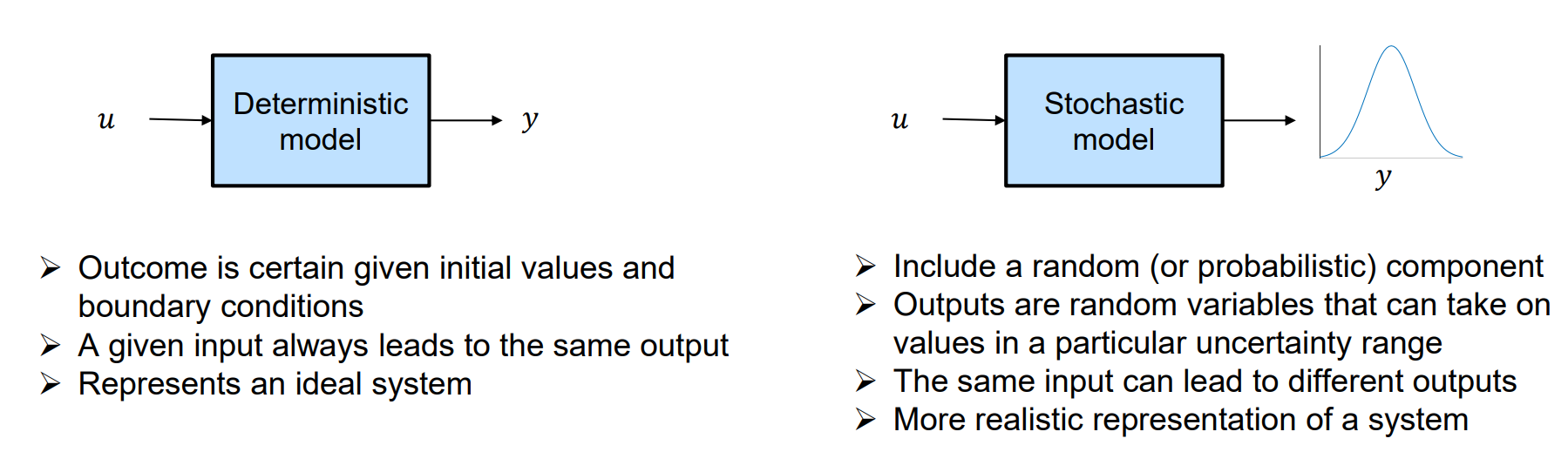
We can classify models into deterministic models vs. probabilistic / stochastic models. Whats their key differences ?

Unlike deterministic models that produce the same exact results for a particular set of inputs, stochastic models predict outcomes that account for unpredictability or randomness.

Stochastic models produce an output distribution for any given deterministic input.

A stochastic model can be obtained by associating a probability distribution to several uncertain model parameters and by propagating the parametric input uncertainty through the deterministic model.

Is Statistical data-driven modelling a deterministic or a non-deterministic model ? Elaborate what this model is based on and what its goal is ?

It’s a non-deterministic model. The variables are random (not specific) with probability distribution.

It is based on data. (→ data-generating process)

Its goal is to infer statements about a real-world process (generate knowledge, e.g. make predictions; validate assumptions etc.)

Statistical modeling is the use of mathematical models and statistical assumptions to generate sample data and make predictions about the real world. A statistical model is a collection of probability distributions on a set of all possible outcomes of an experiment.

What is a training data set, what is a test data set?

Data can be divided into training and test data sets.

Our task becomes then to learn the statistical model from the training set such that it can make correct predictions on a new set of data. We test this ability on the test data set.

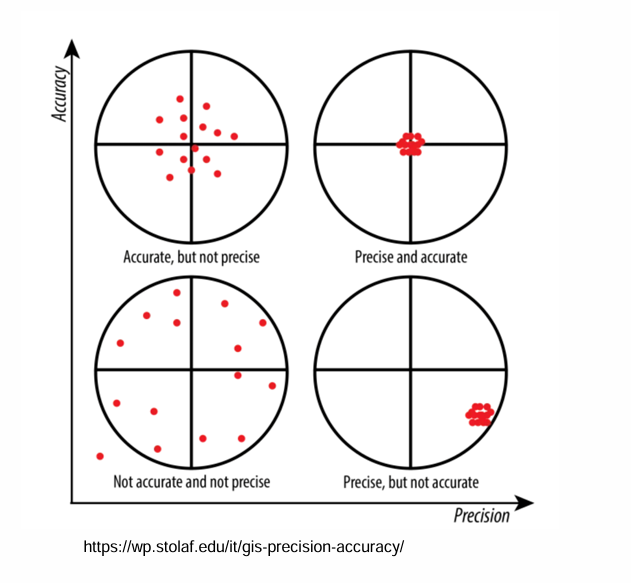
What is the difference between Accuracy and Precision ?

Accuracy: How close are the model results to the actual value of the real system?

Precision: How close are the model results to each other?

What are the different model fidelity levels ? What do they tell about the real system ?

→ They answer the following question: “How accurately does the model need to approximate reality? “

L0: Based on empirical knowledge / rough estimations

L1: Simplified physics principles – limited number of effects considered

L2: Physical behaviour represented by more accurate relationships & equations

L3: Very high computational costs – only local, distinct effects, high precision, high number of features captured

How do we define the complexity of a model ?

1. Computational complexity or algorithm-sided complexity:

• Computational time requirement

• Computational memory storage requirement

often expressed through “Big-O-Notation”: Used to classify algorithms according to how their run time or space requirements grow as the input size grows => measure of computational complexity

2. Problem-sided (model) complexity

• How complex is the model structure?

• Number of parameters / degree of polynomial / independent variables / features / predictors used

3. System-model complexity

• Amount of fundamental (physical) insight about real system

• “reciprocal” of degree of abstraction: higher level of abstraction → lower system-model

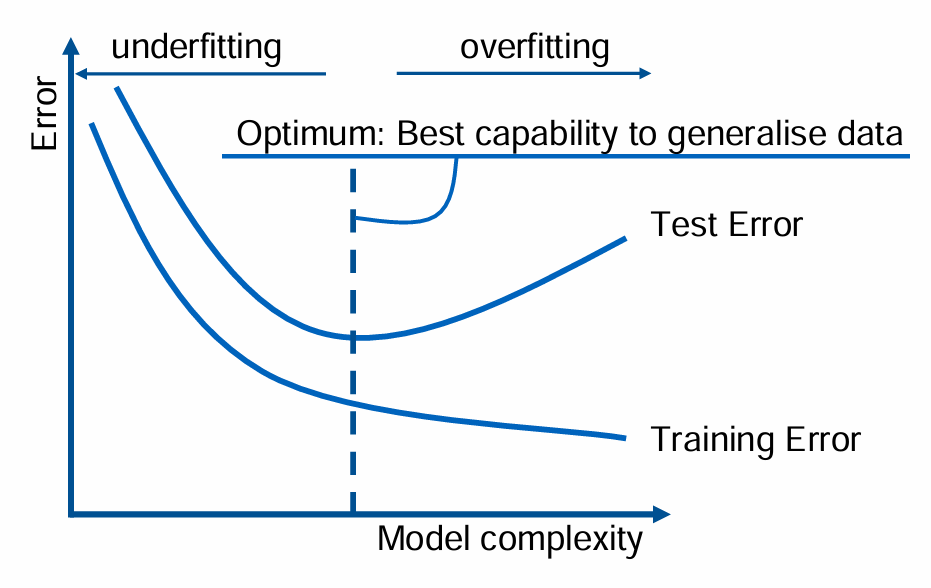
What is “Underfitting” in the context of Problem-sided complexity ?

• Model cannot capture the relevant effects with sufficient accuracy (e.g., nonlinearities)

• E.g. important physical effects have been neglected; polynomial degree is too low; insufficient training in data-driven models

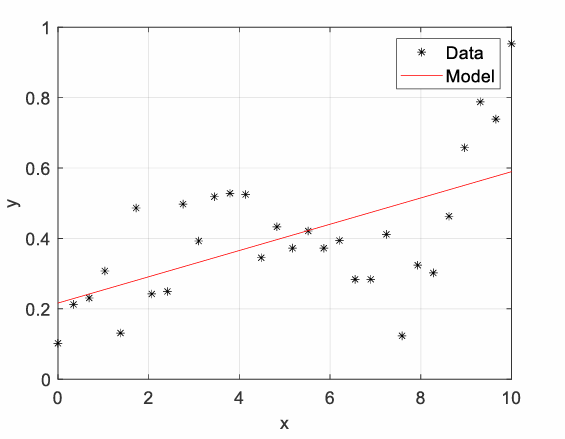
What is “Overfitting” in the context of Problem-sided complexity ?

• Model captures irrelevant info, e.g. noise

• Typical problem of data-driven models!

• Model may be over-trained and cannot generalise from training to test dataset

• Model degree is too high

How do we correct “Underfitting” and “Overfitting” to generalise data ?

How to correct/avoid underfitting:

→ Increase order of polynomial

→ Switch to nonlinear model

How to correct/avoid overfitting:

→ Decrease order of polynomial

→ Decrease ranges of factors

→ Increase number of training sets

Define “ Cross-Validation Error” and how do we obtain it?

Cross-Validation Error = Wow well does the model generalize?

Procedure:

1. Randomly split training data into 𝑞 equal subsets

2. Remove first subset & fit model to remaining data

3. Predict removed subset using model fitted to remaining data

4. Remove second subset from data set & fit model to remaining data

5. Predict removed subset using model fitted to remaining data

6. Iterate till there are no subsets left

What is the definition of “Degree of abstraction” ?

Refers how far a physics-based model distances itself from reality in terms of physical insight. The higher the degree of abstraction, the lower the model complexity

! Important: Low degree of abstraction ≠ Correctness !

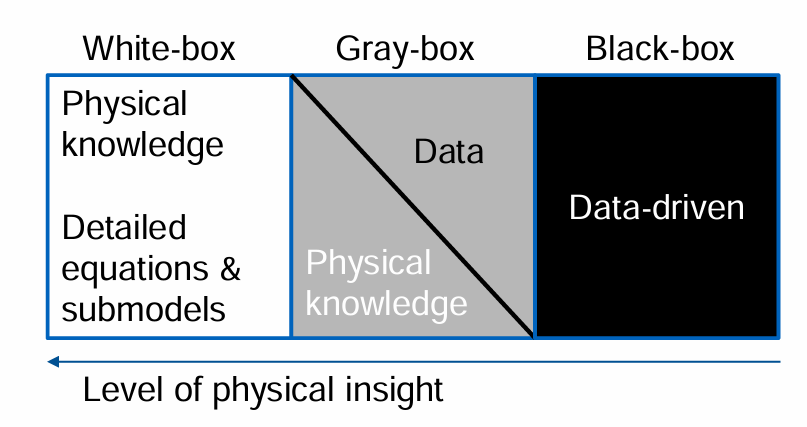
What do “White-boxes”, “Grey-boxes”, and “Black-boxes” model ? What are they useful for ?

→ They model the degree of abstraction of a system and how much physical insight is used for the system

White-box modelling:

• Complete understanding of inner system structure, system boundary & interaction with its environment

• Physical law-driven

• Can be difficult or impossible to obtain

→ suitable when system is simple & well-understood

Gray-box modelling:

• Limited knowledge of inner system structure, system boundary & interaction with its environment

• Captures essential system information

• Partly data-driven

→ suitable when system is partially understood & has complex components

Black-box modelling:

• No knowledge of inner system structure

• Only IO-behaviour

• Statistics/Machine Learning used to build model

• Can capture complex behaviours that are hard to model physically

• Fully data-driven

→ suitable when system is highly complex, not well understood & experimental

What are “Parametric-” and “Non-Parametric” model types ? What are their differences ?

Parametric Models:

• Based on finite set of parameters

• Response is a functiono of input variables and parameters

→ e.g. polynomial structures

Non-Parametric Models:

• Parameter space is infinite-dimensional

• No assumptions on distribution of the data

• Number of parameters can grow with amount of data considered

→ e.g. clustering

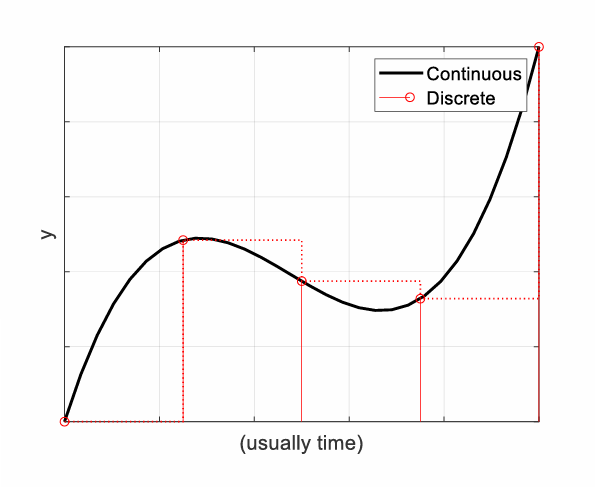
How do we classify models into Continuous- vs. Discrete Models?

Continuous models:

• output changes continuously over time

• assumed behaviour of many physical models

e.g. set of ordinary differential equation

Discrete models:

• Output changes only at discrete points in time

• Computer-based models are discrete

e.g. state machine

In addition to classifying models according to “Continous-” and “Discrete-” Models, how else can we classify models accordingly?

→ Classify models according to domains they cover

(e.g. aerospace, propulsion, structure, gravity, flight dynamics etc. … )

Where do we start when modelling a system? Whats the general high-level approach ?

1. Identify & formulate problem

2. Specify key questions & define objectives: what information and what accuracy are desired?

3. Identify potential modelling approaches

4. Evaluate modelling options (consider degree of abstraction, level of fidelity, (computational) complexity, uncertainty, etc.)

5. Choose the most suitable modelling technique (expected gain and the “effort” required to achieve this gain → trade-off

6. Clarify model architecture, consider system boundaries, define final assumptions (How do model elements interact with each other ? How does the system interact with its environment? )

7. Implement model

8. Inspect model quality: is it realistic enough? Does it meet the requirements?

9. Use the model to solve the initial problem

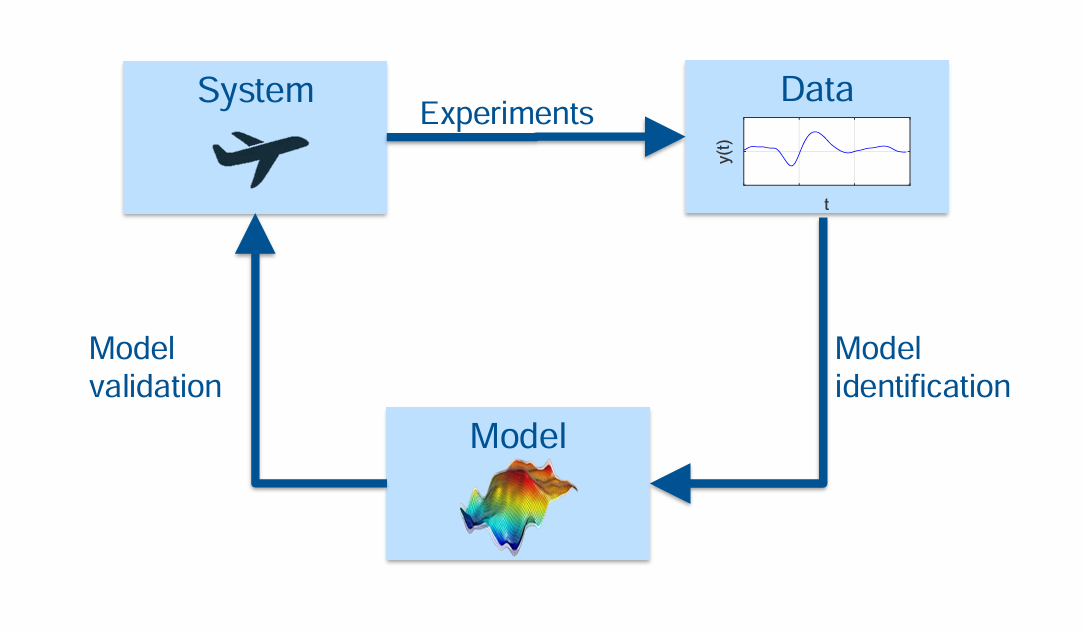
What is System Identification and Why is this beneficial/crucial especially for Aersoapce ?

System Identification = Derive a model of a dynamic system from (experimental) data

by essentially caputing Input-Output Behavior.

Pros:

• Does not require a priori knowledge

• Potentially both computationally efficient and accurate models

• Intrinsic validation possibility

• Can be used to simplify complex model structures

Cons:

• Less or no physical insight

• Models tied to tested system: hard to generalise

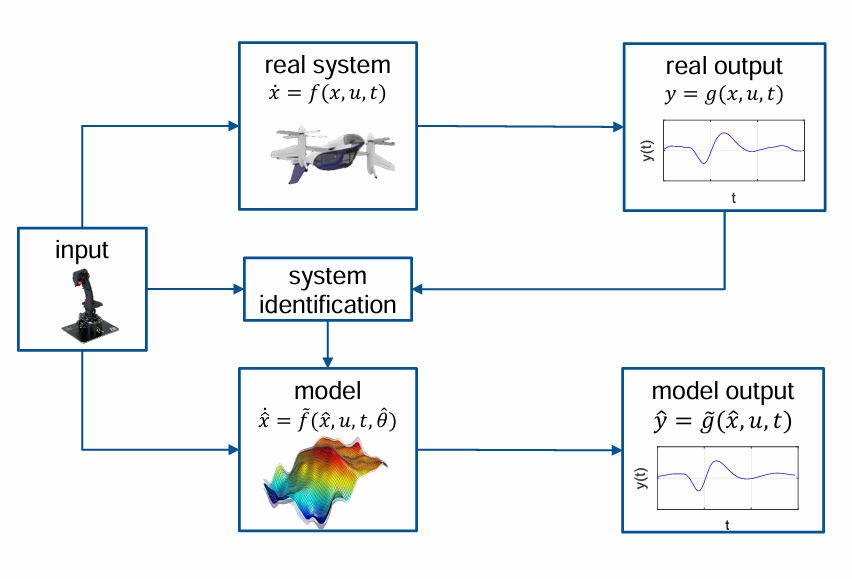
What are the main steps in identifyiing a system?

Main steps:

1. Design & perform experiments

2. Define model structure

3. Estimate parameters

4. Validate model