AP Calculus AB Unit 2

2.1 The Idea of Limits- The average and instantaneous rate of change, which leads to the concept of slope of a curve at point P., 2.2 Definitions of Limits- the average and instantaneous rates of change, which will lead to the concept of slope of a curve at a point P.

Derivative of e^x

The derivative of e^x is just whatever x is at that point

Equivalence Conditions

If one of them, all the others are implied, but there’s no order to assume:

• “The slope of the tangent line to f(x) at x=a.“

• “The slope of the curve f(x) at x=a.“

• “The instantaneous rate of change of f(x) at x=a.“

• “The derivative of f(x) at x=a.”

Slope constantly changes at e^x, etc. curves don’t maintain steady slope

Gallileo’s Law

Assuming negligible air resistance the distance, y, in feet fallen after t seconds of a body in free fall is governed by Gallileo’s Law: y=16². (That is, a body dropped near the surface of the Earth will fall a distance proportional to the square of the time is has been falling, thus giving the equation y=kt². On the Earth, the constant of proportionality is 16.)

Δy/Δx

([where you end up]-[where you started])/time ellapsed

Final-initial OR initial-final as long as numerator & denominator stay equivalent

Language in Questions

For answers, say the same language back to them on the exam

Notation for derivative

(d_y)/(d_x)=Δy/Δx=(y₂-y₁)/(x₂-x₁)

Slope of a Line

To help us in this, recall the concept of the slope of a line. The slope of a line through the points (x₁,y₁) & (x₂,y₂) is defined as m=(y₂-y₁)/(x₂-x₁) (m is no longer used in this class). This is elementarily conceived as the “steepness“ of the line, but is more formally thought of as the change in the y values with respect to change in the x values.

Definition (Average rate of change of a function over an interval)

The average rate of change of an arbitrary function y=f(x) with respect to x over the interval [x₁,x₂] is

Difference quotient

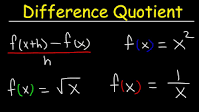
Limits of Polynomial Functions

If p is a polynomial function, limx→a p(x) is calculated by limx→a p(x)=p(a). Any limit of a polynomial can be found by direct substitution.

In a polynomial function, limx→a p(x) & limx→a+ p(x) are calculated as limx→a- p(x)=limx-a+ p(x)=p(a) because limx→a always exists in polynomial functions

Limits in Rational Functions

For those values of a for which the denominator of the function r is not 0, limx→a r(x)=r(a) if r is a rational function

Vertical Asymptote

A vertical asymptote is a vertical line x=a, which the graph of a function approaches as x approaches a.

Average and instantaneous speed

Assuming negligible air resistance (dropped without exerting downward velocity, y₁=0), the distance, y, in feet fallen after t seconds of a body in free fall is governed by Galileo’s Law: y=16t². (That is, a body dropped near the surface of the Earth will fall a distance proportional to the square of the time it ha been falling, thus giving the equation y=kt². On the Earth, the constant of proportionality is 16).That average speed of the object during an interval of time is found by dividing the distance covered by the time elapsed. (Recall that d=rt, thus r=d/t)

Average Rates of Change and Secant Lines

Δy/Δx

[where you end up]-[where you started]/time elapsed

Final-initial OR initial-final as long as numerator and denominator stay equivalent

As Δx gets smaller (the 2 points get closer, Δt→0) it gets closer to tangent/slope/derivative/instantaneous rate of change

The slope of a line through the points (x₁,y₁) and (x₂,y₂) is defined as m=Δy/Δx=(y₂-y₁)/(x₂-x₁). This is elementarily conceived as the “steepness“ of the line, but is more formally thought of a the change in y values with respect to the change in x values

Secant v.s. Tangent line

Secant=average, “passing through twice“

Tangent= instantaneous, “touching once“

Definition of the Average rate of change of a function over an interval

The average rate of change of an arbitrary y=f(x) with respect to x over the interval [x₁,x₂] is Δy/Δx=[f(x₂)-f(x₁)]/[x₂-x₁]=[f(x₁+h)-f(x₁)]/h, h=/=0, h=Δx because h=Δx is less messy/confusing

[f(x₁+h)-f(x₁)]/h is the difference quotient

Geometrically, the rate of change of f over [x₁,x₂] is the slope of the line through the points P(x₁,f(x₁)) and Q(x₂,f(x₂)). In geometry, a line joining 2 points of a curve is secant to the curve. So the average rate of change of f from x₁ to x₂ is the slope of the secant to the curve through the points P(x₁,f(x^₁)) and Q(x₂, f(x₂)).

Working definition of a Limit

If f(x) becomes arbitrarily close to a single number L as x approaches c from either side, we write lim_x→cf(x)=L, and say that the limit of f(x) as x approaches c is L.

• “x approaches c“ means that no matter how close x comes to the value of c, there is always another value of x (different than c) in the domain of f that is even closer to c.

• The limit does not depend upon the value of the function

Relationship between f(c) and lim_x→cf(x)

3 cases occur:

1. f(c) undefined at c, therefore f(x)=/=L (case is true when L does or does not ex)

   i. f(c) is undefined, L does exist

   ii. f(c) is undefined, L does not exist

2. f(c) exists at c, but f(c)=/=L (case is true when L does or does not exist)

   i. f(c)=/=L

   ii.f(c) exists, L does not exist

   *1 and 2 contain an open circle (undefined). Bad in Calculus, cannot do calculus at c in any case

3. f(c) exists at c, and f(c)=L )(we really love this in Calculus), definition of continuity at a point preview

Indeterminate forms

0/undefined

0/0

∞/∞

One-Sided Limits

To have a limit L as x approaches c, as function must be defined on both sides of c and its values f(x) must approach L as x approaches c from either side. If f fails to have a 2-sided limit at c, it may still have a 1-sided limit, that is, a limit is the approach is only from 1 side. If the approach is from the right, the limit is a right-handed limit. From the left, it is a left-handed limit.The

Theorem (Relationship between 2-sided and 1-sided limits)

A function f(x) has a limit as x approaches c if and only if it has left-hand and right-hand limits there and these 1-sided limits are equal.

lim_x→cf(x)=L <-> lim_x→cf(x)=L and lim_x→cf(x)=L

<-> If an only if is the strongest type of theorem