Unit 5 - Fourier Analysis of CT Signals + LTI Systems

Fourier Analysis

one of the most widely used techniques in signal processing; about representing signals as sums of pure sinusoids of different frequencies (e^jwt); merely a special case of LT analysis in which sigma = 0

Fourier Analysis allows for?

convenient visualization of the frequency or “spectral” content of a signal

Spectra

basically a plot of a signal vs frequency instead of time; used to analyze bio signals

Sinotrial Node

the heart’s pacemaker; innervated w/ parasympathetic and sympathetic fibers for neural heart rate control

Spectra Analysis of HR(t)

allows selective assessment of the integrity of the parasympathetic and sympathetic nervous systems

Fourier analysis is simplier than what?

LT bc no ROC so can be applied to causal or non-causal signal, symmetry properties can be exploited in FA

Fourier vs LT

fourier: 1D (w), simplier bc no ROC, applied to causal or non-causal signals, sinusoids instead, and studies of signals

LT: 2D (sigma + w), ROC, applied to just causal signals, permits frequencies domain analysis of exponentially-growing signals, and study of unstable systems

Fourier Analysis is not applicable to what?

exponentially-growing signals and unstable systems no matter how sinusoids are added, a growing signal is never possible

Fourier analysis is preferred for what?

when the signals for study are bounded

Basis Set of Vectors

any vector can be represented as a sum of vectors which span the entire vectors space

Orthogonal

vectors perpendicualr to each other

Signals may be similarly represented as what?

a sum of “orthoginal basis of signals”; ex. representing signals as a sum of shifted impulse fcns (convolution and output to any input) and representing signals as sums of sinusoids (multiplication and input limited)

Fourier Series (FS)

an expansion of usually a periodic signal on a set of orthogonal basis signals; individual coefficients contain the amplitude and phase information for thier respective basis signals

Orthogonal Series Expansion

a set of signals orthogonal signal set on [t1, t2] are pairwise orthogonal on [t1, t2] (have to signify time interval); if Kn = 1 for all n, then the set is said to be “orthogonal” (unity length)

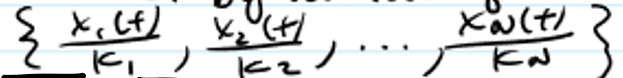
Orthogonal Signal Set

can be always be made orthogonal by dividing each signal by its length; ex. sinusoids

Exponential (or complex) FS

several forms of the FS; forms use different but closely related basis signal sets; has compactness and ease of mathematical manipulation

EFS of a Signal

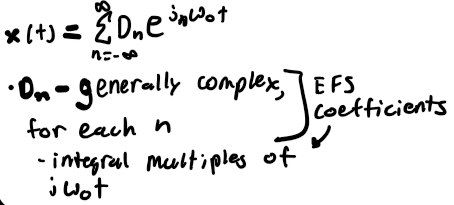
How to compute Dn

take inner product between x(t) and each e^(jnwot)

EFS Pair

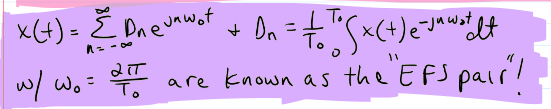
EFS can be computed over what?

a single period of a periodic signal x(t) and it will be valid for all time t; replace t w/ (t +To) in the sum

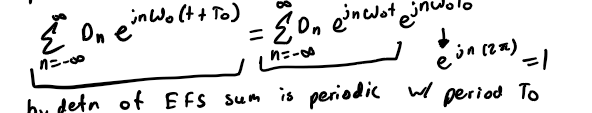
Customary to use what to compute Dn

the primary period [0,To]; can be shown that any period may be employed

If Dn is computed over some range [to, to + To] for a signal, periodic or not?

the EFS sum will represent a periodic version of that signal over the “expansion range”

EFS can be computed over what?

any finite interval and will be valid over that interval; if an interval is a period of a periodic signal then EFS will be valid for all t; why EFS is most commonly used for periodic signals

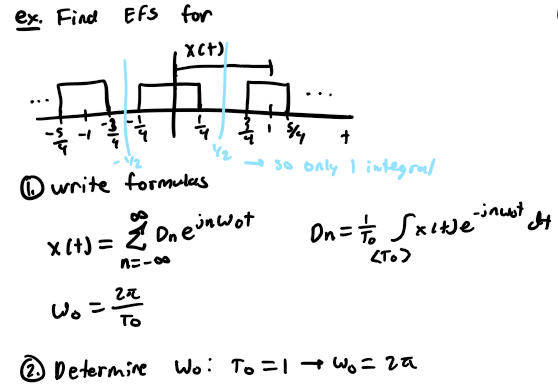
put example in

nth Harmonic

combination of the +- terms of the EFS sum; of the signal being expanded

Conjugate Symmetry

most important symmetry in Fourier analysis; Dn = Dn* → if go same amount in either direction, Dn is conjugates of eachother

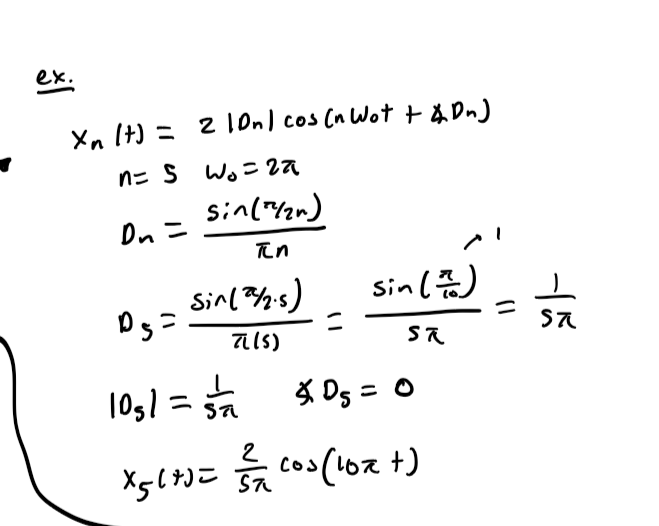
Symmetry Properties

helpful in Fourier analysis;

1. x(t) real → Dn is conjugate symmetric (D-n = Dn*)

2. x(t) real and even → Dn real and even (D-n = Dn)

3. x(t) real and odd → Dn purely imaginary and odd (D-n = -Dn)

4. x(t) is odd-half-wave-symmetric (OHWS) → only odd harmonics “survive” (Dn = 0 for all even n)

5. Do represents average value of x(t) over the expansion integral

Odd-half-wave-symmetric

OHWS; shift signal to the left or right by ½ of its period and then flip it over the x-axis; if it is the same signal as the original, it has this

A level (DC) shift in a signal causes what?

a change in only Do and vice versa

Scaling a signal by A has the effect of what?

scaling the EFS coefficients by A

Shifting a signal in time has no effect on OHWS but does affect what?

even and odd symmetry

Line Spectra

sketch of the EFS coefficients as a function of n → Dn vs n; Dn usually complex so there are 2 plots

2 Dn Plots

amplitude spectrum and phase spectrum

Amplitude Spectrum

plot of the magnitude of Dn vs n (|Dn| vs n)

Phase Spectrum

plot of the angle of Dn vs n

Line spectra allows for what?

visualization of the harmonic content of a signal

Finite # of harmonics can be used to approximate x(t) if

|Dn| is decreasing as n increases

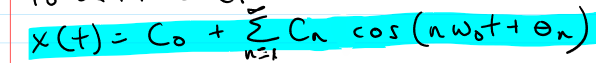
Compact Trigonometric FS (CTFS)

How to compute CTFS coefficients?

compute Dn

Go from An, Bn → Cn, deltan → Dn

Symmetry Properties

1. x(t) is even, Bn = 0 for all n (sum of sines is odd)

2. x(t) is odd, An = 0 for all n (sum of cosines is even)

3. x(t) is OHWS, An = Bn = 0 for even n

4. Ao represents the avgerage value of x(t)

How to get Dn for n < 0

D-n = Dn* bc x(t) must be real to use TFS

Line Spectra

used as informative to sketch then line spectra for the CTFS as the EFS; 2 plots: amplitude spectrum (Cn vs n, n = 1,2,3) and phase spectrum (deltan vs n, n = 1,2,3)

n-harmonic

if know n, know frequency nWo

Bandwidth of x(t)

frequency beyond which there is no power in x(t)

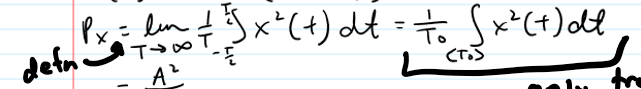
Power Relations

the second one is only true for periodic signals

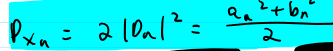
Parseval’s Relations

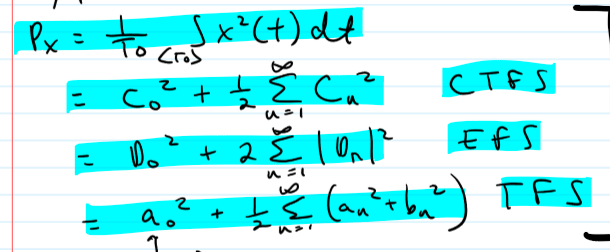
Power is conserved in what

the frequency-domain; summing the square of a signal in time or frequency gives the same value for power; most signals are aperiodic

Fourier Transform (FT)

w/ the FS, periodic signals can be represented for all t as a sum of everlasting sinusoids (only certain discrete frequencies needed); permits the representation of aperiodic signals as a sum of everlasting signals (a continium of frequencies is required)

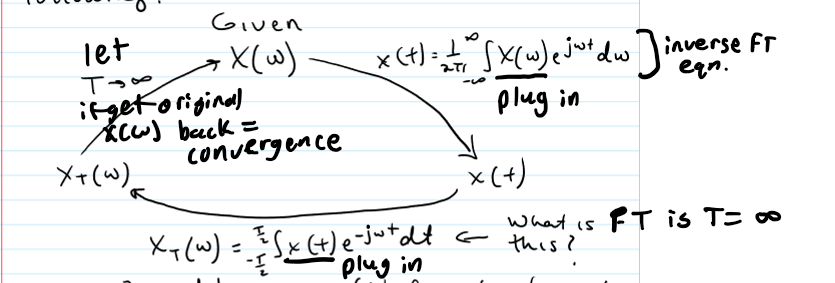
How to derive the FT?

a limiting process is applied to the FS (EFS)

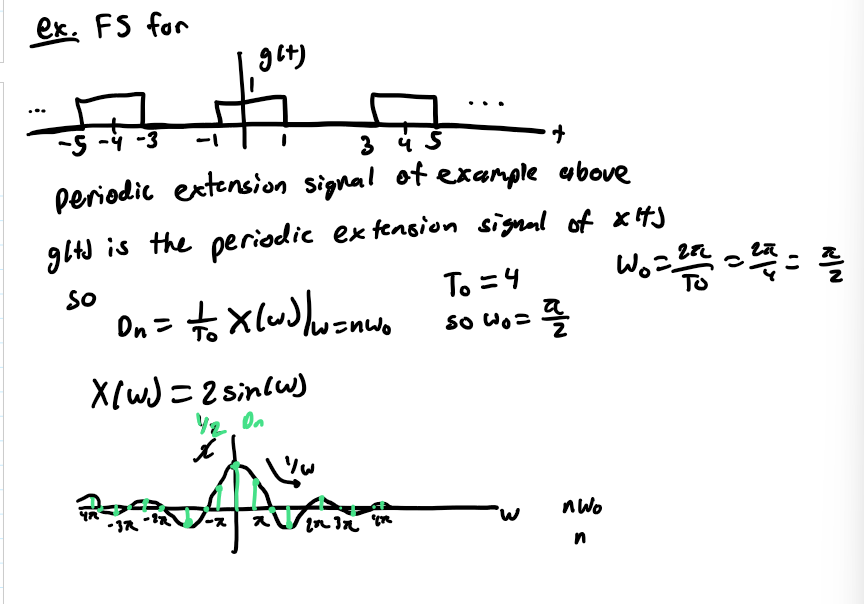
Periodic Extension Signal

has a period To; constructed by repeating the signal every To sec; ex. XTo(t)

FS representing XTo(t)

is periodic and also represents x(t) which is aperiodic in the limit as To → infinity

Example

An aperiodic signal can be represented as what?

a sum of sinusoids w/ a continium of frequencies

Coefficients of the Sinusoids

for any given signal x(t) can be computed as X(w) = integral from - infinity to inifinity of x(t)*e^(-jwt)dt (FT eqn.)

FT Pairs

x(t) and X(w); x(t) ←> X(w)

Periodic Signal - Comment

Dn reflects the extent to which the nth harmonic contributes to the signal

Aperiodic Signal - Comment

X(w)dw reflects the extent to which e^(jwt) contributes to the signal

Spectral Density

amount of frequency component per unit frequency; ex. X(w)

At any single frequency, X(w)dw = what?

0; amplitude of any one sinusoidal component is 0; a whole lot of nothing is something; ex. infinity * 0 = a finite value

X(w)

represents the relative amount of component at frequency w

FT can represent what?

finite duration signals w/ everlasting sinusoids

Relationship between FS and FT

X(w) - FT of an aperiodic signal x(t)

DN - FS of the periodic extension signal XTo(t)

FS Coefficients

scaled “sampler” of the FT of one period of the periodic signal; as To increases, Wo decreases and as To → infinity, Dn → 0

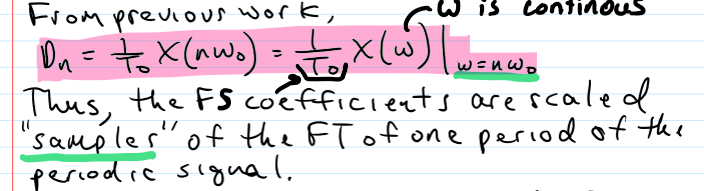
FT Examples

Sinc Function

important in signals and systems; even fcn of w; = 0 when sin(w) = 0 except at w=0; sinc(0) = 1; exhbits osicallating behavior w/ period 2pi and amplitude decreasing as 1/w; never goes to 0

FS Example

FT Pair

any time you have an infinite intergral it could blow up or diverge so FT does not exist for all x(t)

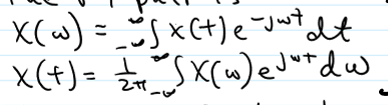
Convergence of the Integrals

x(t) Conditions thet Guarantee Convergence

x(t) is absolutely integrable (all BIBO stable impulse responses are Fourier transformable)

x(t) is square integrable (if get a finite value) → all energy signals are FTable

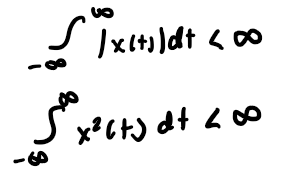
Neither Signals

do not have a FT bc they blow up over time; no matter how you add sinusoids, can’t produce a growing signal

Fourier Transform → Laplace Transform

by setting s = jw; “evaluating LT along jw-axis”; can only do this if ROC includes jw-axis (“causal signals” need all poles to be in the LFP so ROC is right of right most pole)

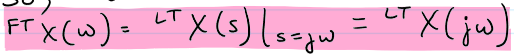
Plot of X(w) vs w

allows visualization of the frequency content or “spectral” content of a signal x(t)

X(w) is generally complex

2 plots

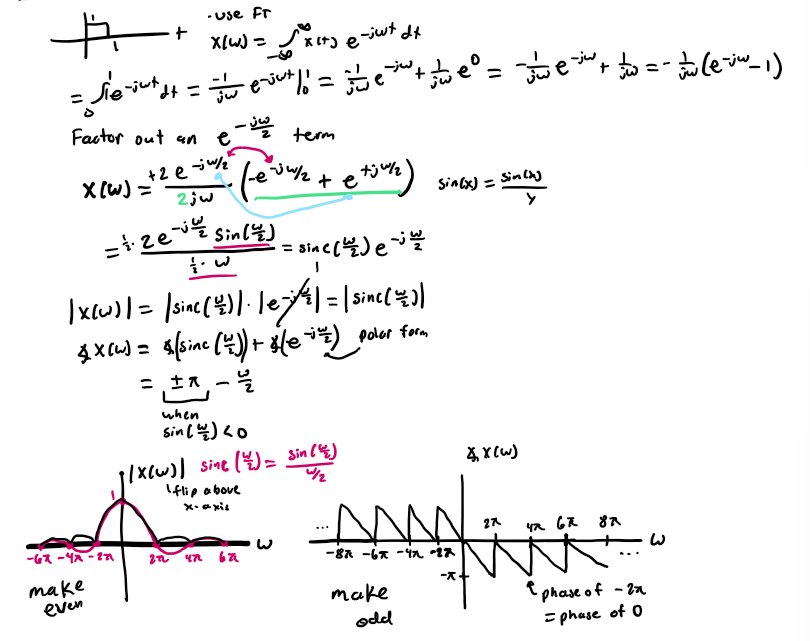
amplitude/magnitude spectrum (plot of |X(w)| vs w)

phase spectrum (plot of angle X(w) vs w)

analogous to EFS line spectra

|X(w)|² vs w

energy density spectrum plot; given instead of magnitude spectrum sometimes

Example

For real x(t)

|X(w)| vs w is always an even fcn; angle X(w) vs w is always an odd fcn; X(w) is a conjugate symmetric

Sketch the Spectra for x(t)

EFS Line Spectra

indicate harmonic content of a periodic signal

FT Spectra

provides similar info that EFS line spectra does for periodic signals but for aperiodic signals

Why does X(w) over a range of frequencies must be approximated?

contribution of any 1 frequency is nothing; need every frequency for aperiodic signals

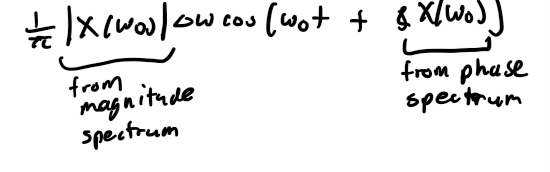
Parseval’s Relation for the FT

energy conserved in FT domain (sum the square of a signal in time or frequency gives the same value for energy)

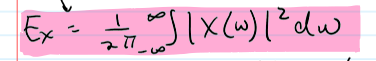
Energy Density Spectrum

plot of |X(w)|² vs w

|X(w)| is what at any single w?

0; reflects the realtive energy at that frequency

Power Signals

include periodic signals as well as constants and the step fcn; niether absolutely nor square integrable

FT of Power Signals

does not exist in the conventional sense

What has to happen if a signal has periodic and aperiodic parts?

analyzed separately

FT of a Power Signal

may be determined with a trick in which impulses (delta(w)) are allowed in X(w); so X(w) is infinite at some frequencies

A complex sinusoid of frequency Wo has a FT given by what?

an impulse fcn located at the same frequency

Power Signals and the FT

doesn’t exist in the conventionl sense; only the inverse FT works

FT of the Periodic Signal

let Dn be the EFS coefficients for an arbiterary periodic signal w/ period (2pi)/Wo; now use lineraity + the result from pervious example to get

2 Steps to Compute the FT of a Periodic Signal

determine EFS (Dn and Wo) then put in formula

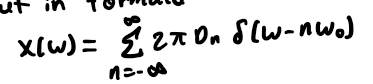
FT of a real sinusoid contains what?

2 impulses; at +- frequency of the sinusoid

Time-Frequency Duality of the FT

operations required to go from x(t) to X(w) and then from X(w) to x(t) are nearly identical (w/ the exception of the 1/(2pi) scale factor and sign on the exponent); ex. time-shifting and frequency-shifting

FT and Inverse FT are essentially Symmetric Formulas

means that for any result or relationship but with x(t) + X(w), there exists a dual result or relationship obtained by interchanging the roles of t and w in the original result

Properties of the LT

linearity, symmetry, scaling, reversal, time-shifting, and frequency shifting

Linearity

if x1(t) ←> X1(w) and x2(t) ←> X2(w), then ax1(t) + bx2(t) ←> aX1(w) + bX2(w)

Symmetry

if x(t) ←> X(w), then X(t) ←> 2*pi*x(-w); if 1 pair of an FT is known, another pair automatically results