MA 175 Discrete Math Proof Schemas
0.0(0)
Card Sorting
1/12
There's no tags or description
Looks like no tags are added yet.
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
13 Terms
1
New cards
Direct Proof (conditionalization)
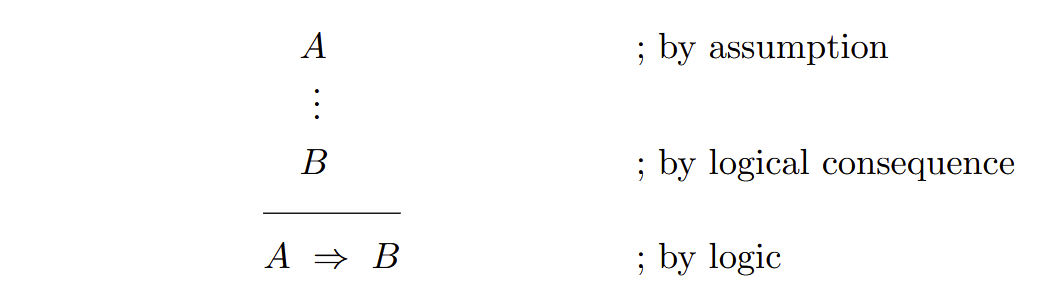
2
New cards
Introduction of the universal quantifier
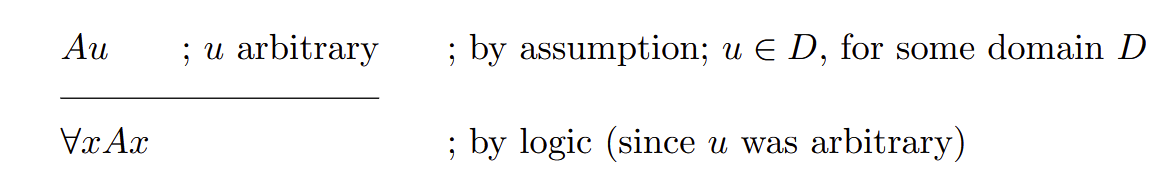
3
New cards
Direct Proof (generalization)

4
New cards
Elimination of the universal quantifier

5
New cards
Existential quantifier introduction

6
New cards
Bi-Existential Inference

7
New cards
Proof by cases

8
New cards
Proof by contraposition

9
New cards
Proof by contradiction

10
New cards
Mathematical Induction (language of properties)
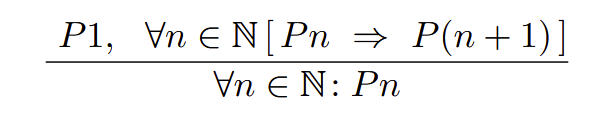
11
New cards
Mathematical Induction (language of sets)
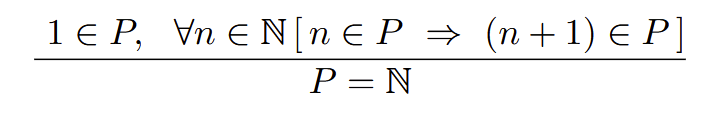
12
New cards
Prove by contradiction
assume P and ¬Q and derive a contradiction
assume both P and ¬Q, and deduce some other contradiction R∧¬R.
13
New cards
Prove the contrapositive
assume ¬Q and show ¬P
prove P→Q by assuming ¬Q and reasoning until you obtain ¬P.