Revision guide

Write doewn the vertex and range and domain (such that it has an inverse
If you are asked to find range or domain of any quadratic equation convert it into completed square form
And then remember the rule
y=a(x−h)2+k
Step 2: Check the sign of a

• If a>0 → parabola opens upwards → minimum value is k

• If a<0 → parabola opens downwards → maximum value is k

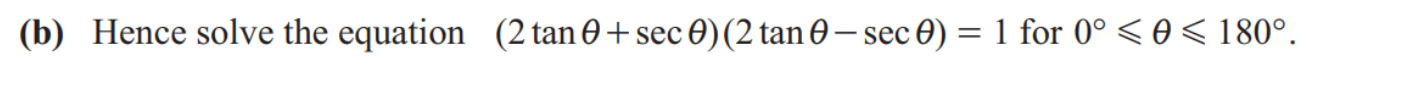
Just know that the answers need to be within the range

If you are asked to graph y 4|x-1|

Remember it is the same as y= | 4(x-1) |

If you are asked to solve
sin 4x = ½

Sin y =1/2
4x = sin ^-1 (4/2)

• (x−3)(x−7)>12

• (x+2)(x−6)<15(x + 2)(x - 6) < 15(x+2)(x−6)<15

• (x−5)(x−9)≥20(x - 5)(x - 9) \geq 20(x−5)(x−9)≥20

• (x+4)(x+8)<−16(x + 4)(x + 8) < -16(x+4)(x+8)<−16
  Can you solve this

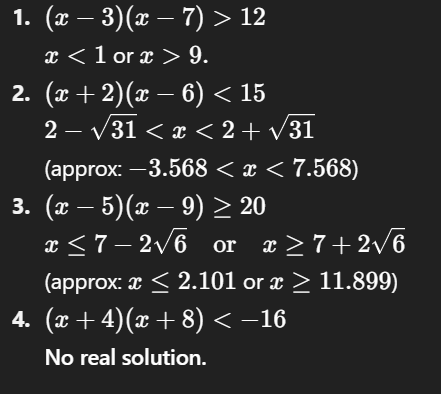
Find possible values of K
For each of these values of k, find the coordinates of the point of contact of the tangent with the curve.

k = + 10 , -10
(2,-6) (-2,6)

Algebraic division of cubic equations
click space

Know how to use factor theorem and remainder theorem

a = −8, b = 15

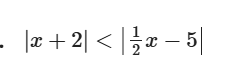
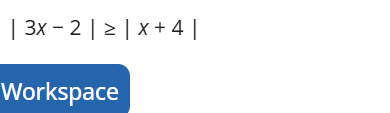
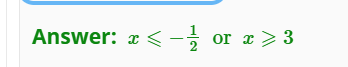
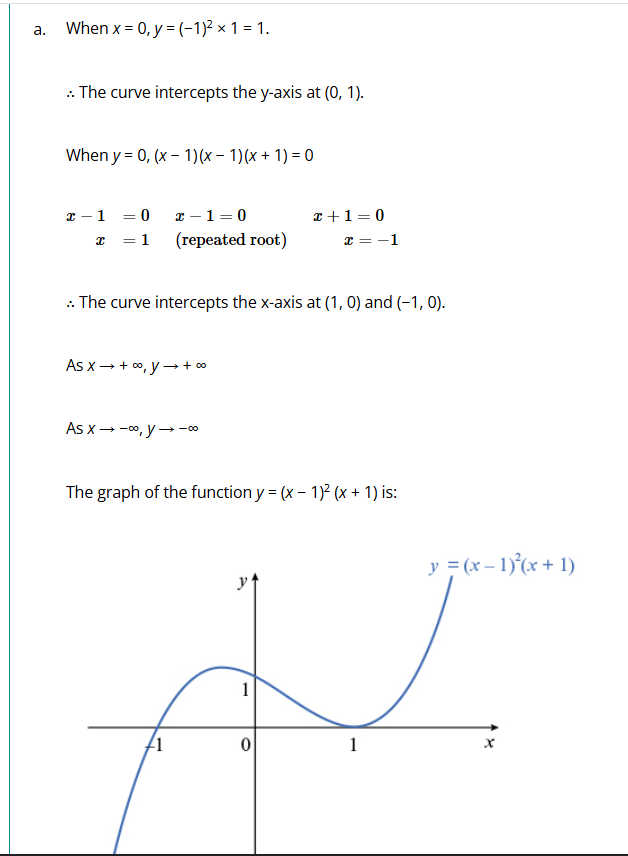
This viedo exactly tells u how to sketch cubic graphs, its modulus and how to solve cubic inequalities
graphically

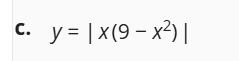
Some special question
Graph it

working on the next flashcard

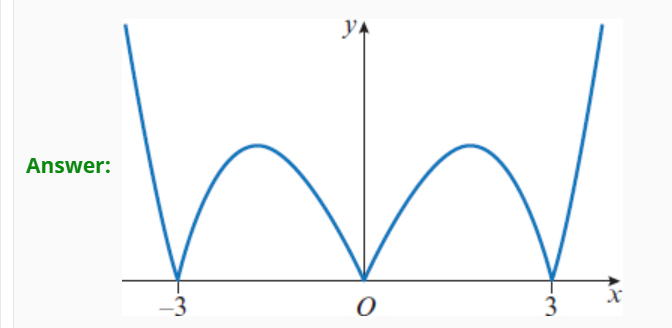
y intercept is 0

It is very easy just take your time to think about it

And the modulus you can do it (pg85)
Similar question 4.3 5d

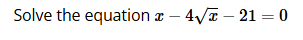
Click space

Click space

What is the asymptote and the range?
2e^5x+8
2e^-5x+8
-2e^5x+8
-2e^-5x+8

y=8
y>8

y=8
y>8

y=8
y<8

y=8
y<8

What is the asymptote and domain
y=−3ln(6x−9)

x=3/2
x<3/2

Things to remember when graphing the exponential funtions

Draw a line between two inverse function

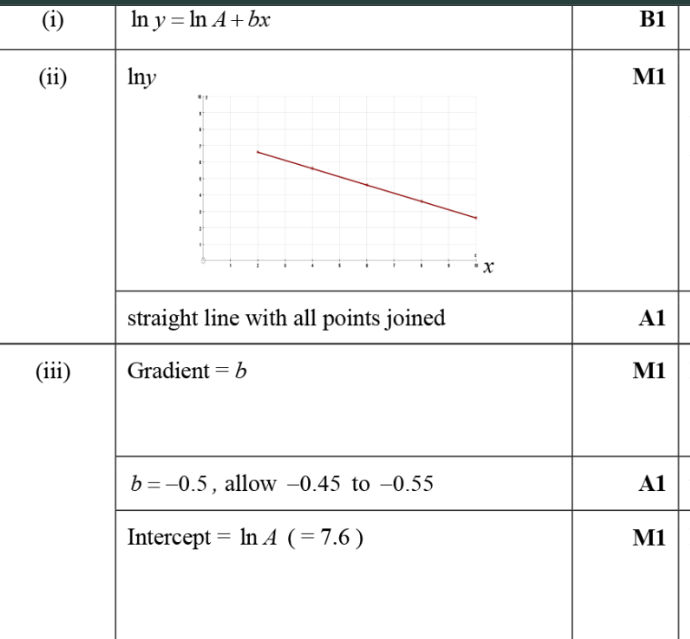
(iii) Use your graph to find values of A and B

How to find the period of tan cos and sin graphs
Given that y = a(sin or cos or tan) bx + c

tan graph = 180/b
sin graph = 360/b
cos graph= 360/b

Just substitute the 1

Remember that ln(1) = for non calculator

0

Remember that
-ln(a/b) =
ln(?)

ln(b/a)

Recall

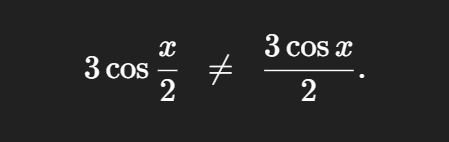
recall

very important rule

remember this

Know this this is where ayush makes the most mistake

Learn how to use first derivative test