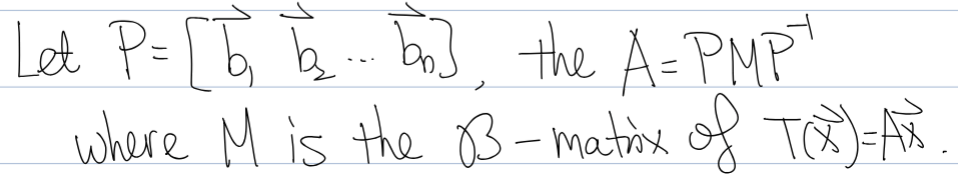MATH 3A Final Theorems and Definitions

Properties of inner product

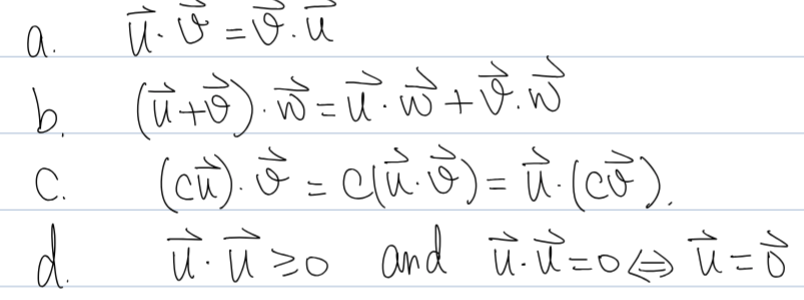
The length (or norm) of a vector is

Unit vector is

The distance between two vectors is

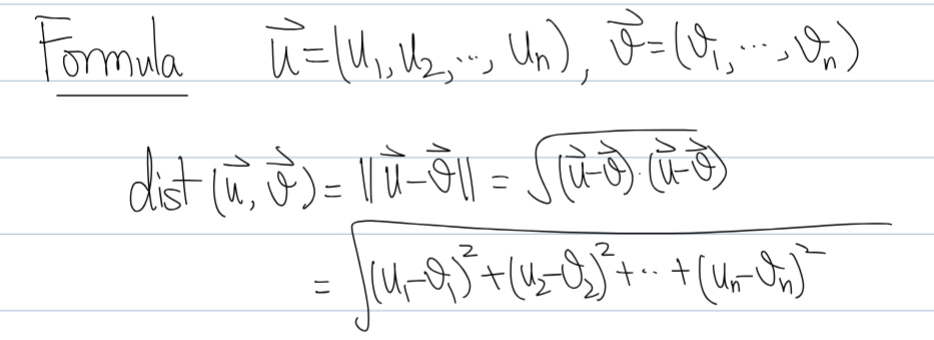
The distance squared is

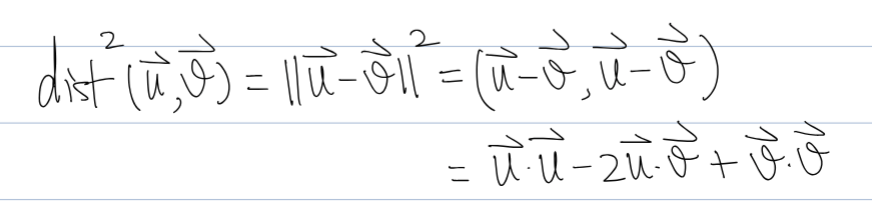
Definition of orthogonal

If a vector z is orthogonal to every vector in a subspace W then…

z is said to be orthogonal to W

The set of all z that are orthogonal to W is called the orthogonal complement of W denoted by W┴

x̅ is in W┴ if and only if

x̅ is orthogonal to every vector in W

W┴ is a subspace in IRⁿ

(Row A) ┴ =

Nul A

(Col A) ┴ =

(Nul A^T)

Pythagorean theorem

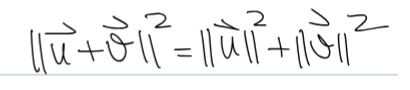
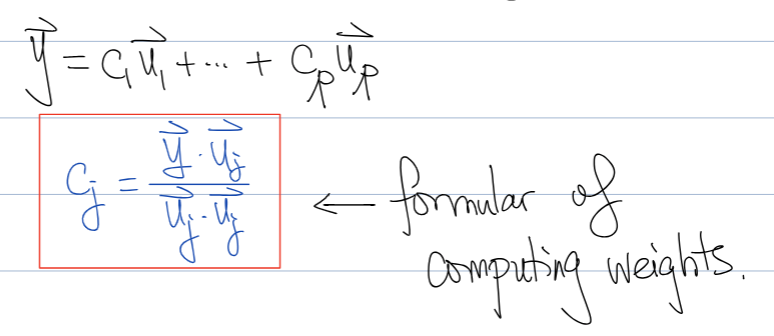
If S = {u₁ … u_p} is an orthogonal set of non-zero vectors in Rⁿ then …

S is linearly independent

S is a basis of span {u₁ … u_p}

Orthogonal basis definition

for a subspace W of IR is a basis of W and it is also an orthogonal set

Orthonormal set definition

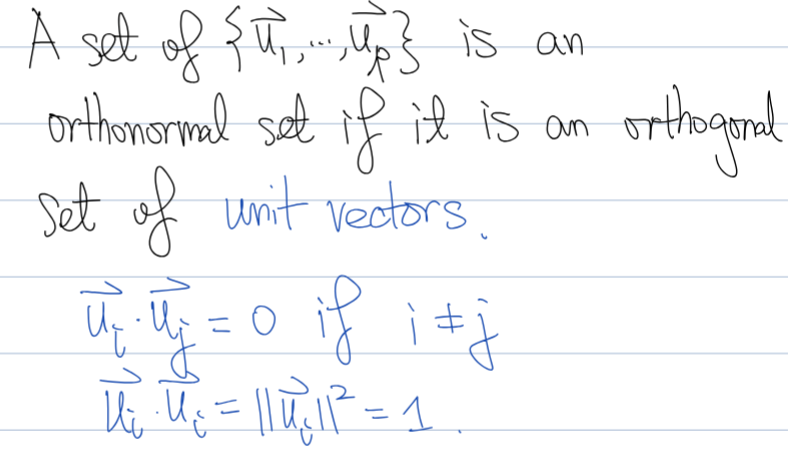
If U is a square matrix we call it

an orthonormal matrix

An mxn matrix U has orthonormal columns if and only if

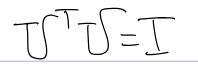
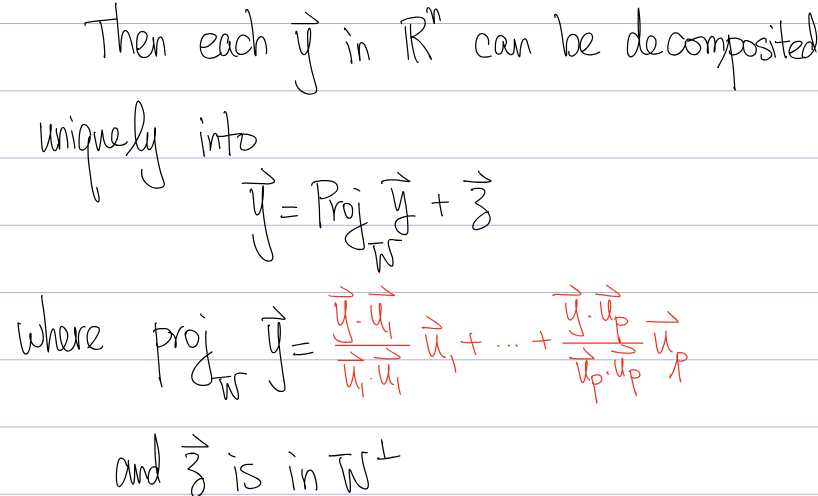
The eigenvalues of triangular matrix are…

the diagonal entries

If v1…vr are eigenvectors of distinct eigenvalues, then…

{vi … vr} are linearly independent

Similarity definition

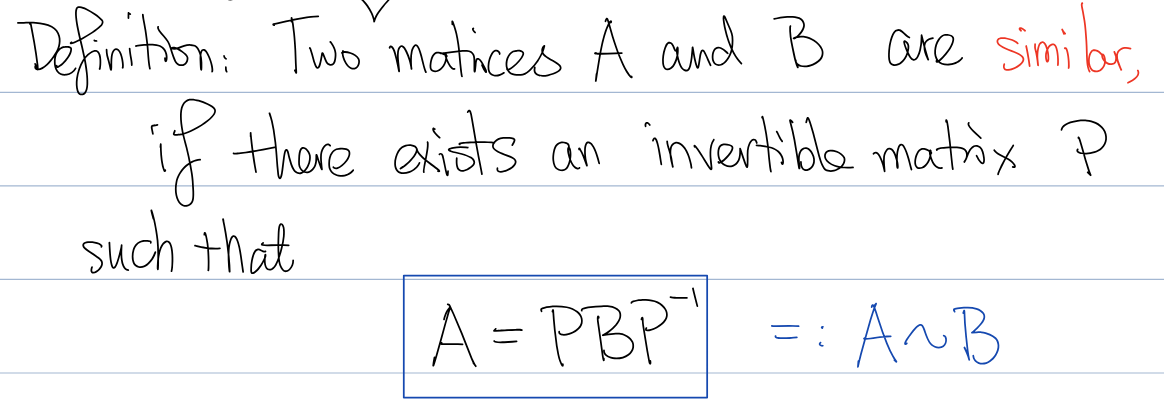
If A ~ B, then

their characteristic equations are the same

If there are distinct eigenvalues (eigenvalues with multiplicity 1) then…

The eigenvectors are independent

For eigenvalues with multiplicity = r_k > 1 check if dim Nul (A-λI) ≤ r_k

If dim Nul (A-λI) = r_k then there are r_k independent eigenvectors

If dim Nul (A-λI) < r_k then there are not enough eigenvectors

An nxn matrix A is diagonalizable if and only if…

A has n linearly independent eigenvectors

An nxn matrix with n distinct eigenvalues is

diagonalizable because their eigenvectors are linearly independent

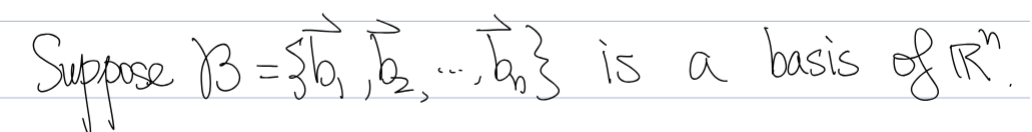
*If the question asks you to find the B matrix (or M matrix), use B/M = P^-1AP