Chapter 2: Conditional Probability

Conditional probability

of the event A given the information that event B has occurred is denoted by P(A|B) and equals

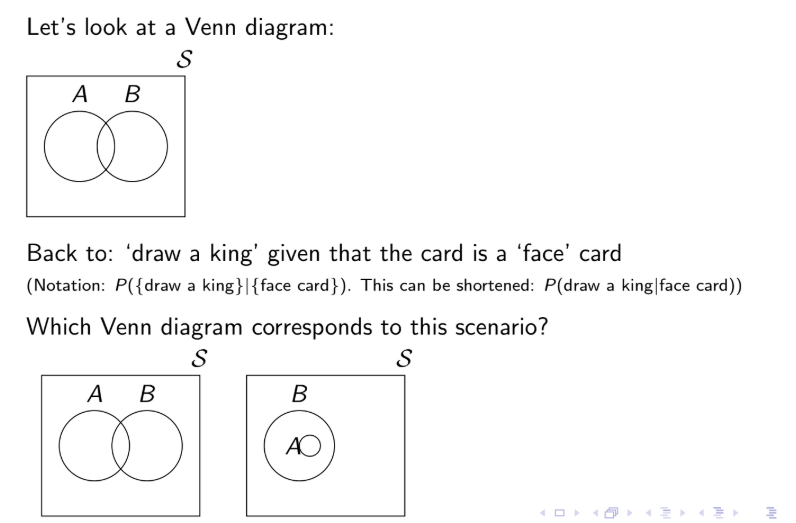
Example: someone rolls a 6 sided die and tells you the result is even. What is the probability it is a 4 given that it is even? (Ans: 1/3)

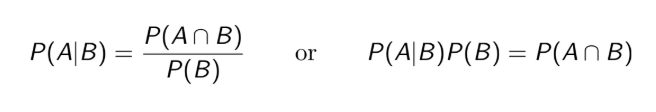
Inutuition

if we say “given” or “conditional” on an event occurring, the effective sample space has changed.

Conditional Prob: Emails and spam

Example: about 50% of all emails are spam (S)

0.5% of all emails involve a subject line that is all-caps (C)

Given an email contains in all-caps subject line, the probability is not spam is .11 (P(S^c|C))

Some practice questions:

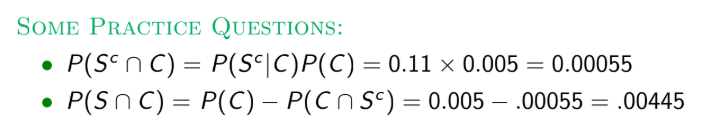
Definition of independence

Two events A and B are independent if ‘information’ about event A doesn’t provide ‘information’ about event B

Two events A and B are __ if ‘information’ about event A doesn’t provide ‘information’ about event B

independent

two events A and B are independent if and only if

This means we can conclusively prove events are independent or not

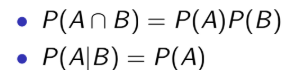
Independence and disjoint are not the

same

If two events A and B are independent

1. A^c and B are also independent

2. A and B^c are also independent

3. A^c and B^c are also independent

Summary: Effectively, any combination of events and complements are independent

Multiplication rule

The law of total probability (LOTP)

let the events A1, A2,…AK be disjoint and make up the entire sample space:

Large Hardon Collider

At the CERN Large Hardon Collider (LHC), fundamental particles like the Higgs Boson (HG) can be created. Two primary detectors, ATLAS and CMS, are designed to find the HB

There is another secondary detector, LHCb, that can be used

bayes theorem

Consider events A and B. Suppose we know the conditional probability of A given B. Now, we want to know: Given that A has occurred, what is the probability that B occurs? Consider events A and B. Suppose we know the conditional probability of A given B. Now, we want to know: Given that A has occurred, what is the probability that B occurs?